大型极小曲面壳体数字化建造*

苏朝浩，王俊聪 ，陈庆军，邓能涛，王子安，张枢健

引言

在数学中，极小曲面是指平均曲率为零的曲面[1]，即是满足某些约束条件的面积最小的曲面。物理学中，由最小化面积而得到的极小曲面的实例包括了沾了肥皂液后吹出的肥皂泡。晶莹剔透的皂液膜，是满足周边空气条件和肥皂泡吹制器形状的表面积最小的表面1）。由于极小曲面种类多样，且极度轻质化，因此而受到了建筑师的青睐。其中，德国人弗雷·奥托（Frei Otto）是最早涉及该领域的先驱之一2）。1961 年，他开始进行了一系列肥皂泡的实验，以寻求通过最少的材料达到最大的面积；随后，将其在张拉结构方面的研究成果应用到1972年慕尼黑奥林匹克体育场中[2，18]（图1）。日本人伊东丰雄与奥雅纳事务所合作，开发极小曲面的结构技术[3]，运用到台中歌剧院的设计当中，产生了戏剧化的空间效果（图2）。近年来，随着数字化设计和制造技术的迅猛发展，数字设计先锋开始尝试发掘极小曲面的种类和艺术潜力，将其作为构筑物或者建筑空间而转化。法国人马克·福尼斯（Marc Fornes）及他的团队设计建造的一系列如Zephyr 凉亭（图3）的极小曲面装置，采用双层3mm 厚的铝板作为制作材料，推进了极小曲面在轻薄特性上的发展[4]。扎哈·哈迪德（Zaha Hadid）建筑事务所和苏黎世联邦理工学院（ETH Zurich）合作采用3D 编织模板制成的双弯曲混凝土壳体[5]，提高了实现极小曲面的经济性（图4）。与此同时，国内对极小曲面的研究也有所发展，由南京艺术学院徐炯老师带领的师生团队建造的双蕊亭装置[6]，采用厚度为0.3mm 的钢板通过材料自承重方式构成物化空间形态（图5），虽然其整体厚度在轻薄方面有了进一步突破，但装置的尺度规模也因自承能力的局限而受到限制。从以上数字化领域的前沿研究成果可见，极小曲面在建筑领域的应用处于一个探索性的实验阶段，在设计与建造方面都有待更深入的探究发展。其中，从纯粹的数学模型向有应用场景的物理模型的转化方式，以及大尺度模型的经济性建造方式，是面向现实转化和推广应用的关键所在。

图2 台中歌剧院中极小曲面结构模型

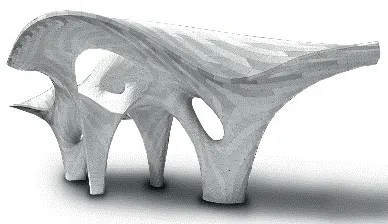
图3 Zephyr 凉亭装置模型

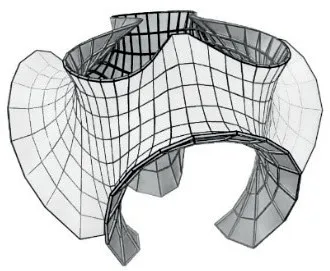
图43D 编织模板制作极小曲面模型

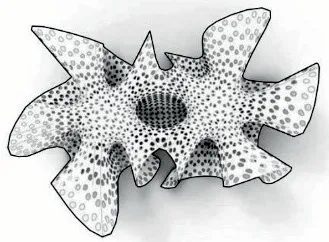
图5 南京双蕊亭模型

图6-a 作品“云间玲珑”位于花城广场中轴线的实景照片图6-b 作品“云间玲珑”近景照片

极小曲面在建筑领域的大尺度转换和实现，实际上可以归结为一种结构艺术[7]，是技术与艺术的高度融合的产物。一方面，是新颖的空间艺术形态；另一方面，是技术的层面突破，包括了生形技术与制作工艺。本文将基于转换的视角，探讨其生形方法、构造方式、曲面拟合流程以及拼装方式等问题，并结合2019 广州国际灯光节作品《云间玲珑》3），展示“极小”和“极薄”背后所蕴含的力学美与空间艺术魅力（图6）。

1 艺术形态

1.1 混沌中的数学美

极小曲面由数学算法生成，外观复杂而多变的混沌状态，实质上是由数学公式生成，蕴含着一种内在的逻辑美感——数学之美[8]。这种抽象的数与形的和谐之美，又带有一丝东方美学的意蕴：朦胧美；与中国传统园林中采用的玲珑石、太湖石有着异曲同工的美学形态（图7）。

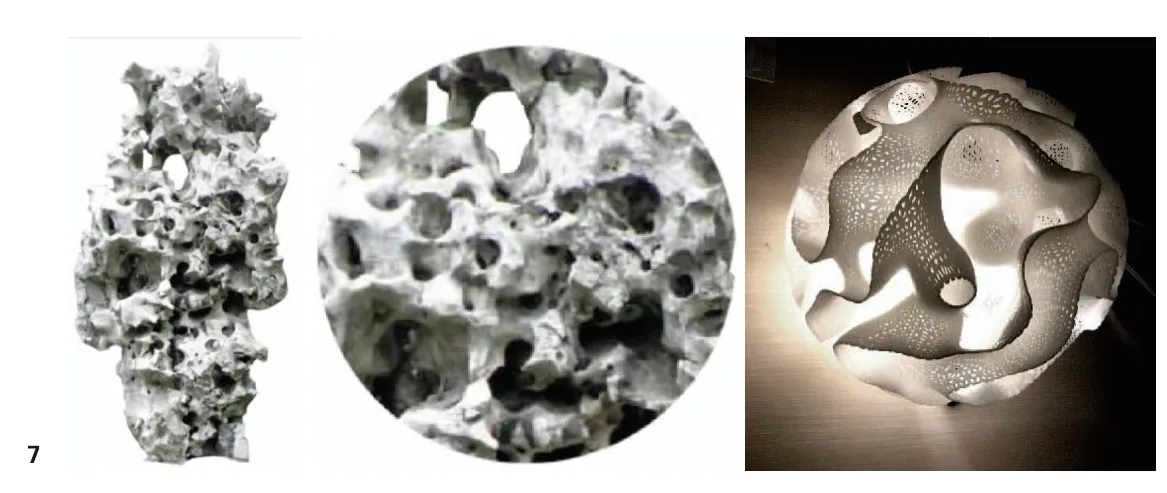
图7 太湖石（左1、2）与小比例3d 打印模型（右1）对比

1.2 新的视觉空间形式动力

区别于正交坐标系标识的线性空间，极小曲面在建筑空间创作方面富有全新的形式动力。一方面，提供一个毫无内、外边界可言的“虫洞空间”，一种别开生面的空间体验，弥漫着神秘的未来科技感。现代建筑的“流动空间”将进一步走向极致，笛卡尔正交坐标系与空间方向性仿佛骤然消失。另一方面，数学公式的变换所产生的空间形态多样性，将源源不断地提供建筑空间创作的丰富题材。

1.3 极轻薄的结构艺术

像肥皂泡那么轻薄到极致，是一种惊艳的自然美学形态。随着算法与参数的变动，呈现出像云、像雾、像花的轻盈的姿态。极小曲面趋同于膜、壳等类型的薄壁结构形式，表现出“以较少的材料建构较大的空间”的自然法则，是一种高度体现效率、经济、美观有机统一原则的结构艺术题材。

2 关键问题和挑战

极小曲面属于高度复杂的异规（Informal）[9]双曲面，其制作存在着两方面的技术挑战。其一，是力学性，即轻薄背后起支撑作用的结构逻辑[10]；其二，是工艺性，即如何利用数控技术制作异规双曲面，并兼顾其效率性与经济性。

2.1 力学性：轻薄背后的结构逻辑

极小曲面是纯数学模型，通过算法生成的形体，并不能完好地适应于现实中的物理工况。譬如，在自重和水平风荷载作用下，轻薄的构件容易失稳而崩塌，承载能力相当有限。因此，极小曲面，作为壳体结构[11]，成立的前提是将数学模型向力学模型进行有效地转化。由于非线性、无定型、复杂化等形态特征，使得这种力学转化显得扑朔迷离、难度极高。因此，如何获取和建构轻薄背后的结构传力形式[12]，进行有效的结构找形，便构成了关键问题和挑战。

2.2 工艺性：异规双曲面的数控建造

首先，对于大型的极小曲面壳体的建造，效率和成本的因素是放在第一位的。无论是采用锻造和人工打磨的传统工艺，还是采用3D 打印的先进技术，都显得不切合实际：时间周期和成本将远大于预期。其次，连续性强、曲率变化多、无规则镂空分布等非线性形态特征，使得制作难度极大，还原度低下。这实际上是强调从设计一直到建造的完整“数字链”[13]，它要求设计师在前期设计中也可以直接参与并控制最终的加工、建造细节。因此，如何找到一种具有制作效率的拟合非规则双曲面的数控方法，构成了实现异规曲面制作的另一个关键问题和挑战。

3 找形方法

找形的方法包括了两个部分：（1）基本形的找形；（2）结构的找形。基本形的找形是指极小曲面的参数化找形方法，是纯数学模型；而结构的找形是指在基本形的基础上考虑了力学条件后的形式重构，是数学模型向力学模型的转化，是本实验的重要环节和关键所在。

3.1 基本形的参数化找形

通常，极小曲面的参数化生成有“box 逼近法”和“marching cubes 法”[14]，“box 逼近法”是通过将空间中的点的值分为大于等于0 和小于0 两个阵营，然后以点为中心生成小box，再提出box 的贴合面并平滑的方法获得极小曲面模型；marching cubes 法则是通过判定穿越每个空间体元中的等值面的形态，而组合而成由小三角形片构成的极小曲面，再同样进行平滑即可获得极小曲面原形。由潘·米查拉多斯（Panagiotis Michalatos）研发的Millipede[15，16]插件工具是基于Grasshopper 平台生形工具，为设计师驾驭非线性力学现象提供了更大的空间，该插件工具实质上属于marching cubes 法。在Millipede工具的Values 端的输入值可以是极小曲面的数学公式，也可以是自定义干扰点的值来描述极小曲面形态。

调整算法：通过基本算法得到的模式较为固定，即使是通过调整计算周期得到不同密度形态，也难以满足多样性空间的诉求。因此，基本算法需要进行改进：将空间内的点变成可操控的点，叠加操控这些点的算法和程序，以实现可大可小、大小相间的具有功能适应性的多样性空间形态。

3.2 结构找形的思路与方法

基于结构概念的找形，主要解决的是非线性、轻薄的数学模型在力学工况下的转化和建构方法问题。轻薄、无规则以及扭曲的形态特征，导致了壳体在空间各个维度的刚度不均衡，难以形成整体的有效刚度与外荷载进行抗衡。为了促使极小曲面向力学模型进行转化，两个结构概念的引入显得非常重要：整体“管状框架（Tubular frame）”和局部“环箍效应（Cyclo-hoop Effect）”。

（1） 由均质泡沫向整体管状框架的异规转化。

首先，从均质的泡沫状连续曲面单元，向集聚状态的管状物体进行变形；第二，将空间分布的管状物进行连接，形成互相拉结的异规管状空间框架；最后，对异规管状空间框架进行调适，形成一种树状的传力模式：由枝丫-次干-主干-地面进行传力。

从技术操作层面上，则是通过上一个步骤中参数化生形的控制点，进行有导向性地移动，将平均分布的极小曲面单元转化为管状物和空间框架。

（2） 发挥空间抵抗作用的薄壁构件的形态转化。

轻薄与扭曲是形成结构刚度的不利因素，因此，需要对薄壁构件的形态进行变形转化，形成有效的空间抵抗作用。一方面，利用环箍效应生成类桶状体，环向的约束可以大大提升薄壁构件在纵向上的承载力和稳定性。另一方面，利用具有正反高斯曲率的曲面单元在管状物之间进行加强连接，以提升整体稳定性。具有正反高斯曲率的曲面单元，呈现出空间抵抗的力学机制，当一个方向发生变形，将由另一个相反方向上的变形进行反向约束，从而形成空间抵抗作用[10]。

（3） 多工况验证与反复调试。

通过结构概念的植入而转化的力学模型，每一个步骤都需要通过量化的有限元结构计算进行验证和调适；而整体模型又需要考虑水平荷载等多工况所产生的影响，综合评价后反复调试，直至满足结构性能要求。

4 制作方法

数字建构的过程中，形式的“生成”与物质化的“建造”需通过数字技术结合起来[17]。基于效率与成本控制的考虑，利用CNC4）技术进行制作是优于锻造和3D 打印的首选方法。

4.1 曲面拟合原理

曲面拟合的原理：先将曲面平面化，以适应CNC 工艺的高效率生产，进而通过平板的弯折拼装以拟合原来的异规双曲面。

4.2 制作流程

具体方法：首先，将异规双曲面进行网格化，当网格足够多，单元尺寸足够小，即可无限接近于原始曲面；第二，将网格进行条幅式分解，便于展开为平面；第三，对条幅单元之间的连接方式进行设计；第四，将带连接方式的条幅式单元进行拍平和排版，通过CNC 技术进行切割；第五，标注网格之间的角度，进行弯折和拼装拟合。

5 “云间玲珑”的实验

5.1 找形

“云间玲珑”作品采用由潘·米查拉多斯（Panagiotis Michalatos）研发的Millipede 插件工具进行生形（软件平台为Rhino 及插件Grasshopper，图8、9）。并在此基础上进一步编制程序，实现对控制点的有导向性操控。

图8 在不同函数约束下的形态对比

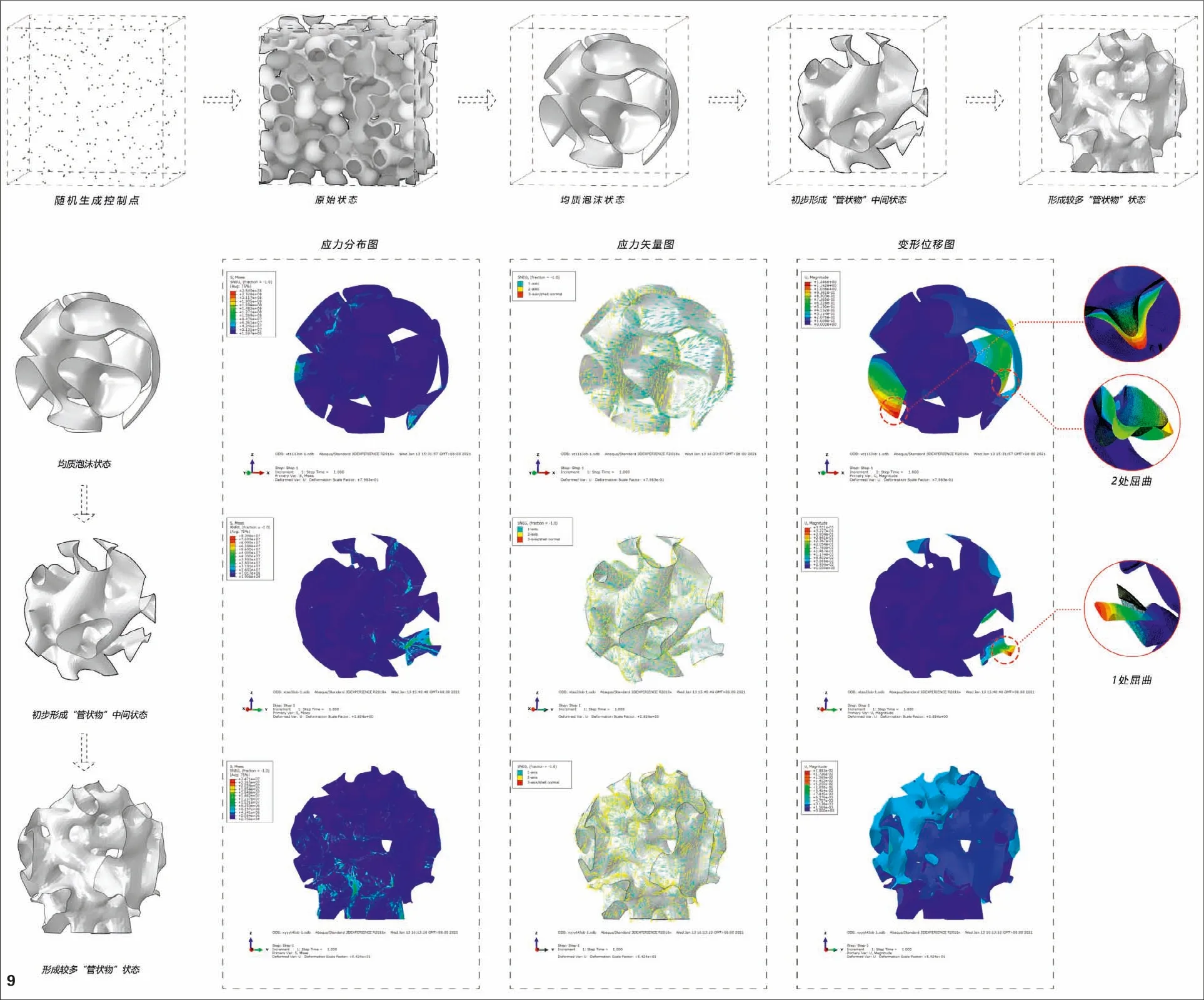
图9 从均质泡沫向管状框架转化的过程

第一，从无规则的连续面单元，向管状的空间形态变形，形成互相拉结的变异空间框架，从而形成有主体框架的整体性空间抵抗作用。从技术操作层面上，则是通过上参数化生形的控制点，进行有导向性地移动，将平均分布的极小曲面单元转化为管状物和空间框架。在数学模型的调适以过渡到合理的力学模型过程中，需要进行反复的力学概念判断、测试和验算（图10）。图中可看到，从均质泡沫到管状物框架逐渐转化成型的过程中，由于轻薄导致屈曲的区域数量逐渐减少，变形量变小，应力集中的现象也逐渐消失，结构的性能趋向优化。

第二，利用环箍效应生成类桶状体，以提升薄壁构件的承载力和稳定性。一方面，提取模型中若干组异形桶状物进行力学计算，虽然非严苛意义上的桶状体，应力分布会受到扭曲的干扰，但是通过观察计算结果可清晰看到环向和竖向上主应力的传递路径（如图10-a），环箍的作用依然有效。这个效应也可通过简单的力学实验加以验证（图10-b）。当通过程序生成的类桶状体数量逐渐增加，局部刚度得到了逐步加强，整体的稳定性也得到了有效保证。

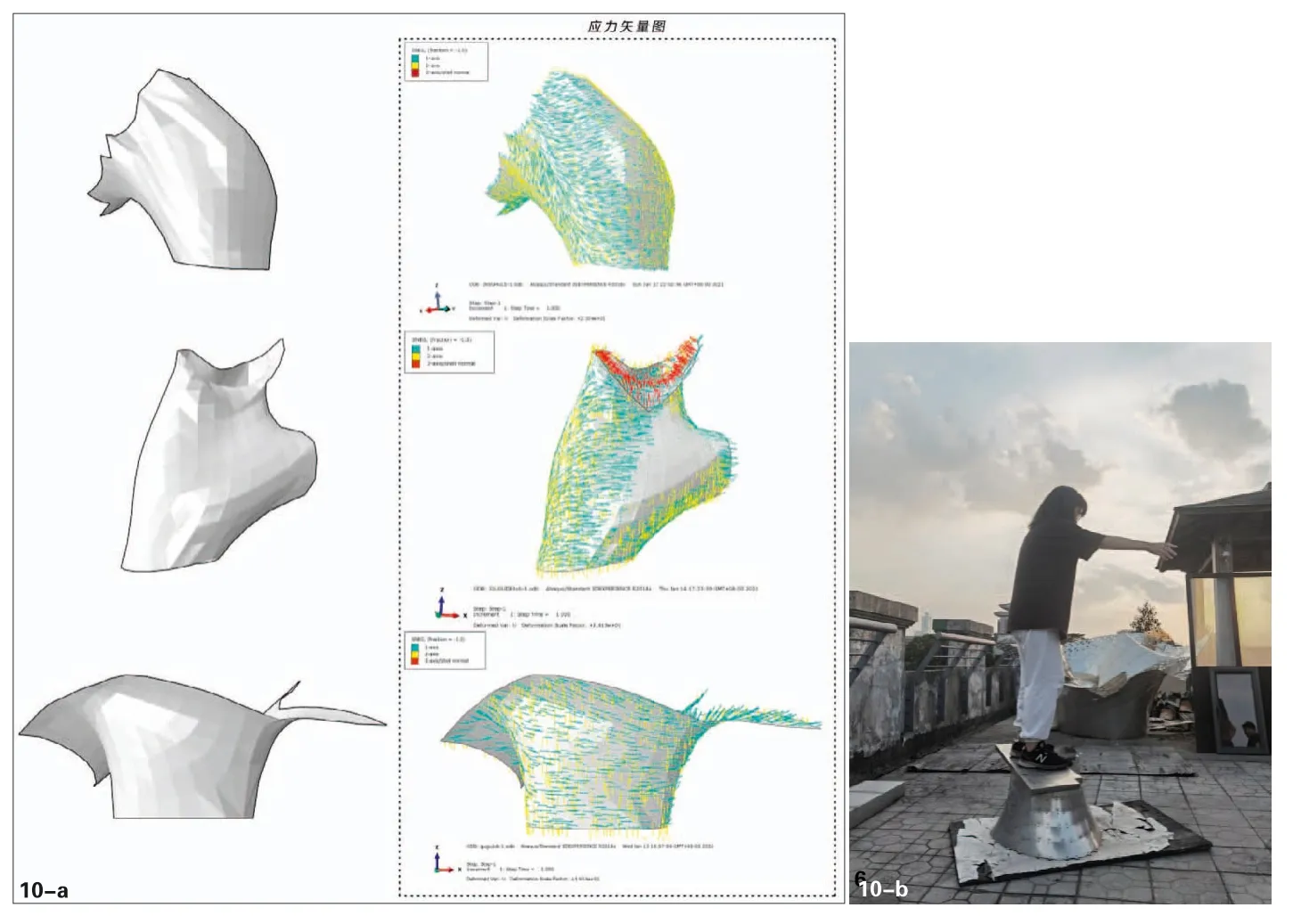
图10-a 几种异形桶状物的环箍效应验算-应力矢量图；10-b环箍效应测试

第三，找寻合理的支撑条件，将重心控制在几个支座的几何中心附近，规避大尺度的悬挑和坍塌（图11）

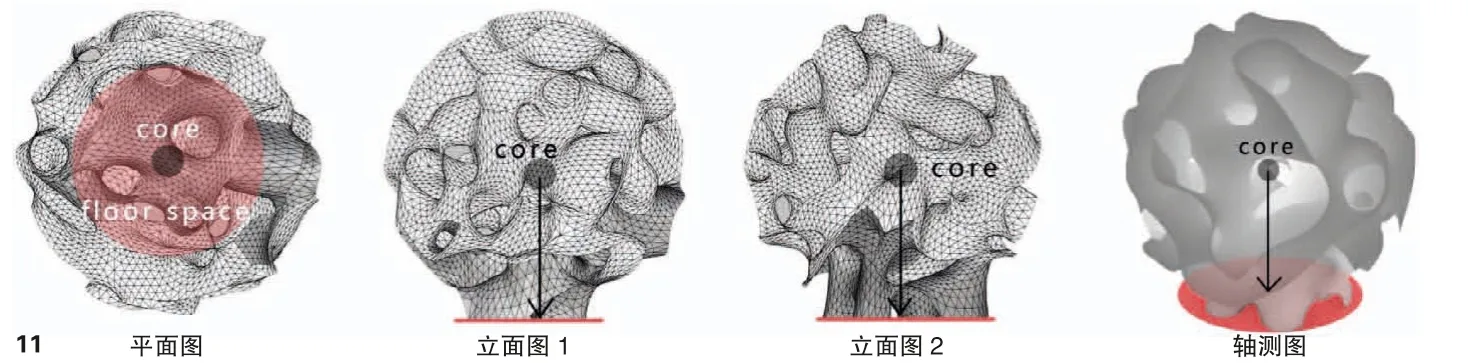
图11 物理中心与底座的关系

第四，多工况验证。经过一系列的优化环节后，将过程曲面模型导入到有限元软件（ABAQUS）中，输入相关的结构参数，进行重力和风力工况下的力学计算及验算（图12-a、图12-b），评判极限应力与变形值，最终形成了具有良好结构性能的目标模型：高度7.8m、直径7.6m 的大尺度模型，所用铝板厚度只有1.5mm（厚度约为球体直径的1/5000），重量只有750kg，可以说是轻薄到了极致。

5.2 数字化制作

5.2.1 网格化

细分级别越高时，细分后得到的三角形网格数量越多，网格曲面模型就越顺滑真实；反之，级别越低时，网格数量越少，网格曲面模型越失真。网格化的单元数量及尺寸大小，一方面跟曲面的曲率相关，另一个方面跟制作的效率相关。当曲率很大时，曲面弯曲扭转急剧，那么网格单元就需要数量越大和尺度越小，以逼近原有的曲面；然而，当数量太大之后，连接单元增加、弯折角度数量增加，导致后续拟合环节的效率降低。因此，网格化，是还原度与效率之间的一种平衡的结果（云间玲珑作品的最终模型划分为16000 多个三角形网格）。

5.2.2 条幅式展开

为了实现在机床上进行平板化生产，网格化后的整体必须进行离散，条幅式离散是其中一种有效的方式。通过编制程序，将相邻的连续三角面单元选择出来，并按照一定的长度范围形成条幅式单元（需要控制一张标准板的尺度范围内，通常为1.22m×2.44m）；因为在长度方向上只有一列三角面单元，所以，只需要将相邻三角面之间的角度拍平，即可将弯折状态的条幅式单元展开为平板，方便切割。（如图13 中步骤3～4）

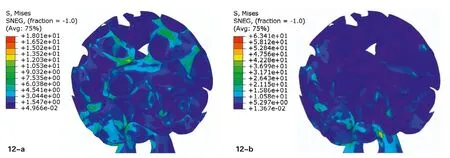
图12-a：重力作用下应力云图，12-b：水平x 方向荷载作用下应力云图

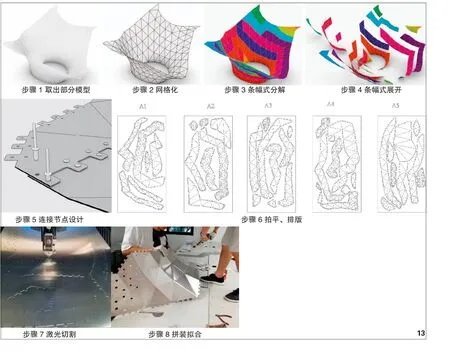
图13 拟合流程

5.2.3 连接节点设计

连接节点指的是相邻条幅式单元边缘之间的相互搭接方式。连接节点设计的逻辑是考虑到搭接边缘的适应性，将三角形单元每个边缘长度进行五等分，并在中间的四个节点处向外延伸出一定距离的正方形耳板，再对耳板的四个角进行圆角处理，最后在耳板范围内挖出两个4mm 圆形孔洞以便铆钉打入。通过耳板设计而实现的密缝对接构造，一方面具有结构稳固性，另一方面也较为隐秘，达到较好的美观程度。

材料名称厚度硬度脆性透光耐候性优缺点对比PE1.5mm 柔软，易弯曲 过度弯折易断裂 具有很好的光晕效果良好抗老化能力优点：光晕效果理想缺点：较软，刚度不足PVC 1.5mm 中等，易弯曲 过度弯折易断裂透光率大长时间暴晒结构不稳定优点：可透光，有层次感；缺点：较脆、刚度不足铝合金 1.5mm坚硬有韧性，不易折断不透光良好优点：强度大、刚度好，韧性大缺点：不透光

5.2.4 拍平、排版和切割

拍平展开即将三维的数字模型拍平成若干个零散的二维平面构成元件，这个步骤实现了复杂三维向简单二维的转化。将带有耳板的条幅式单元进行平面展开，便于CNC 工艺的二维加工，从而获得制作效率。经过条幅式展开后生成的若干“肋条”二维单元，需要

根据二维单元的形状和大小、数控加工机床和材料面幅尺寸来进行排版，达到节省材料和时间的目的。在材料选择和建造工具平台确定之后，数控机床将根据排版好的CAD 图纸进行精准切割。

5.2.5 拼装拟合

分解网格曲面后生成的是若干个带状排列的三角形网格曲面单元，为了便于后期高效加工生产和搭接工序，需对每个三角形网格曲面单元进行编号。同时，每个三角形网格面之间都有一定的夹角，这些夹角的角度标识对后期搭接拼装来说是十分重要的，也是后期将二维材料加工成三维材料的依据，因此在编号的同时也要进行角度标识。

根据编号找到加工完成的铝合金板，此时的铝合金板为二维面板，需要根据角度标识来对铝合金板进行弯折处理，弯折位置为三角形面与面之间交接的边缘线，使二维面板弯折成三维铝板材料。最后，再用铆钉穿过两个对位准确的耳板圆形孔洞，将两个三维铝板单元固定拼合在一起，以此类推拼合还原整体，拟合流程如（图13 中步骤8）。

5.3 材料选择与拟合测试

在材料选择上，进行了三种材料的试验，分别是PE板材料、硬质PVC 板材料和铝合金材料，并做了缩尺试样模型来比较（表1）。PE 板材料（图14）和硬质PVC板材料（图15），属于半结晶性材料，具有低透明度、低光泽度、低刚性、脆性的特性。在试样模型中的效果如图，整体效果较为顺畅，透光率低但营造出了柔和的光感效果，视觉效果上达到了目标要求，但应对外界压力时容易出现弯曲形变，因此不宜作为空间管状框架部分的结构材料，可作为边缘非主体结构部分的材料。铝合金材料具有耐高温、耐腐蚀、强度高等特点，因此，作为管状框架部分的结构材料的首选（图16）；然而，由于不具备透光性，需要对其表面进行开洞处理以达到预期艺术效果。

图14 PE 板材料

图15 PVC 板材料

图16 铝合金板材料

针对于铝合金板材的还原制作，将平面材料弯折拟合为三维状态时必须考虑其原有曲面的曲率因素。假设两个三角折面之间的夹角为α（图17），反映出原有曲面的不平坦程度，也就是曲率的大小。经试验表明：当α=170-180°时，在加工时可免去对折痕标记处的弯折，铝合金板具有一定的韧性能够适应一定范围内的误差，从而拟合的曲面更为平滑；当120°＜α ＜170°时，则在加工时候需要对折痕标记处进行机械弯折；当α ＜120°时，则需要考虑重新优化局部形态以规避形态扭曲导致整体刚度的下降。针对于PVC 和PE 材料两种弹性材料（可弯曲，但无法弯折），则需要在设计阶段严格控制夹角α，当α ＜150°时，拼装拟合原有曲面的难度将变得非常大，误差被放大，导致整体无法拟合。

图17 图左为网格三角面夹角与折痕示意图，图右边为折痕照片

5.4 拼装

对7.8m 高、直径7.6m 的大尺度异规曲面模型进行拼装，将面临两个难题：第一，由于非常轻薄，整体未成型之前结构刚度低，变形大，而单元之间的拼接螺丝孔直径只有4mm，精准的高空作业是一个巨大的挑战；第二，由于运输条件限制，拆分的数量与组装的效率是一对矛盾体。

针对于第一个问题，采用的施工方案是：先组装管状框架，以产生一定的空间刚度，再以管状框架为依托，辅助周边的脚手架进行外围次一级结构的组装，最后结合吊车或者龙门架进行高空部分的作业（图18）。

图18 实验室组装搭建试验

针对于第二个问题，首先充分评估组装时序中每个阶段状态的结构安全性，在此基础上，参考集装箱的国际标准尺寸要求，将整体模型划分为若干个组块，并参照40GP 的集装箱容量进行堆叠摆放模拟；在实验室中，对划分不同组块数量的方案进行拼装演练和优选评估，最终确定为38 组，确保运输的可行性与组装的效率性（图19、20）。

图19 海心沙现场施工过程

结语

通过数学公式生成的极小曲面，具有特殊的数学美与建筑空间艺术感染力。将数学模型进行力学模型的转化，是实现大尺度极小曲面壳体建造的关键环节之一；而在异规双曲面的制作当中，考虑经济性和工艺性等因素的制约，通过参数化设计与CNC 加工技术的紧密结合进行曲面还原，是一个行之有效的成本可控的制作方法；在组装的过程中，则需充分评估和确保各个组装阶段状态下的临时结构刚度，以应对轻薄与柔软所带来的高空精准作业的挑战。2019广州灯光节作品《云间玲珑》仅为极小曲面实验性作品中的个例，创作和研究中存在诸多不足之处,譬如如何实现极小曲面向力学模型转化的自动生形，又如在网格面的弯折步骤中如何结合机器人实现更加智能、高效的建造，等。以2019 广州国际灯光节为契机，大型极小曲面壳体作为灯光艺术的一个全新的载体，展现出独特的数字建筑空间魅力，希望借此抛砖引玉，期待业界在该领域推陈出新，涌现更多佳作！

图、表来源

图1 ～5：作者根据项目图片改绘；

图20 完工状态

图6： 广州市锐丰文化传播有限公司提供；

文中其他图片：由作者绘制或拍摄。

注释

1）在“科普中国”科学百科词条编写与应用工作项目中提到极小曲面的物理学概念。

2）建筑师弗雷·奥托(Frei Otto，1925.5.31– 2015.3.9)的作品从自然现象中寻找建造的灵感，采用模拟自然现象的实验方法来确定形式的过程，也是对自然现象的规律考察的过程。

3）项目信息：项目名称：2019 广州国际灯光节作品“云间玲珑、海心之珠”项目地址：中国广州天河区花城广场海心沙设计方：华南理工大学·何镜堂建筑创作研究院/数字设计研究中心 & 4D 梦工坊设计 & 完成时间：2019 年9-11 月设计主创：苏朝浩、邓能涛、王俊聪、王子安、吉儒刚结构技术：陈庆军、何永鹏灯光设计：杨慧、麦松盛、关诗敏灯光、音乐互动设计：克莱蒙·恩伯（法），黄则玄作品尺寸：高度7.8m，直径7.6m作品材料：铝合金（厚度1.5mm）、PVC、铆钉、蝴蝶钉合作方：广州精宏建设有限公司、广州名实照明设计有限公司、广州梦工坊数字科技有限公司、广东盛世飞扬光电科技有限公司、佛山速派篷房有限公司、广州万林数字科技有限公司

4）CNC，数控机床技术，英文名称为Computerised Numerical Control。

5）感谢华南理工大学亚热带建筑科学国家重点实验室支持。