横摇运动下养殖工船多液舱流场特性数值分析

方舟，徐红昌，戴锦阳

(1.嘉兴南洋职业技术学院，浙江 嘉兴 314031；2.嘉兴市港航管理服务中心，浙江 嘉兴 314031)

自上世纪70年代开始，养殖工船总体构想[1]及大型养殖工船的系统[2]、总体设计[3]陆续展开，其中，液舱晃荡是海洋工程领域中备受关注的热点问题[4-6]。相关研究关注了液舱晃荡对舱体结构的冲击及疲劳影响[7-9]，较少有关于舱内水体流场特性的研究报道。养殖工船在风浪中的摇摆运动使得养殖舱内的水体发生剧烈运动，养殖舱内物理环境指标通常主要考虑水体流速及光照情况，而适养流速一般与鱼体长度有关，如体长在20 cm以上的大黄鱼，养殖舱内水体流速在0.6 m/s以下时对其影响较小。舱内适渔性问题，有学者研究了液舱晃荡对养殖工船适渔性的影响[10-11]。而目前的研究大部分是通过在养殖内进行进水出水状态下的流动特性研究[12-14]，而较少考虑养殖舱在船体运动激励下的动态流场特性分析。为此，考虑基于CFD技术，对某10万t级养殖工船横摇运动下的养殖水舱液舱晃荡现象分析不同横摇频率下的舱内流场特性。

1 理论基础

计算养殖工船液舱内流体为不可压缩连续流体，控制方程为连续性方程，采用k-ε方程湍流模型。液舱模拟为两相流模拟，忽略各相之间的热传递[15]，自由液面捕捉采用VOF方法。

1.1 控制方程

液舱液体为不可压缩流体，连续性方程为

(1)

其动量守恒方程为

(2)

式中：p为流体微元的压力，Fx、Fy、Fz为微元体上的质量力。

1.2 湍流模型

标准k-ε方程模型满足湍流黏性系数各相同性，在该方程基础上引入湍流动能耗散率ε的方程，因此k-ε方程为

Gk+Gb-ρε-YM+Sk

(3)

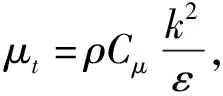
2 数值模型验证

选取Mikelis[16]液舱晃荡实验验证本文所采用的数值计算模型的正确性，液舱长、宽、高分别为0.741 m、0.399 m和0.395 m，液舱几何模型以及横摇中心Y1和Y2位置见图1。液舱横摇运动方程为φy=φ0sin(ωt)，φ0=0.1 rad。实验中在宽度中心壁面处设置7个压力监测点R1～R7，在宽度中心距离左侧壁面0.135 6 m位置布置浪高仪WR。

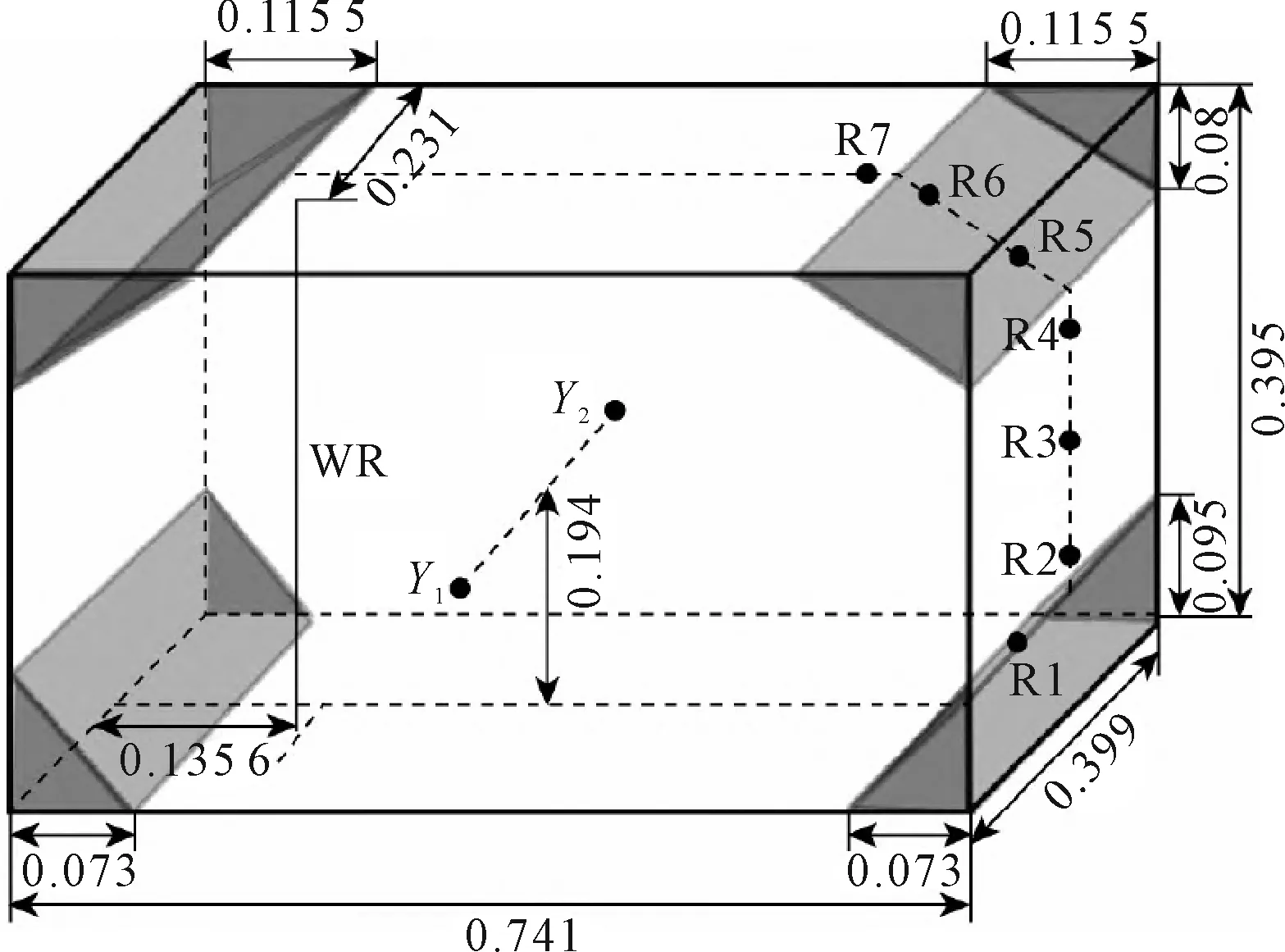
图1 实验采用液舱几何模型

数值模拟中液舱所有边界均设置为无滑移壁面边界条件，模拟实验中充液比为0.9，横摇周期为0.97 s工况。在进行CFD数值计算时需要对网格进行收敛性分析[17]，选用满足一定细化率要求的3组网格进行收敛性计算，3组网格尺寸划分见表1，分别命名为Mesh a、Mesh b和Mesh c，3组网格R3监测点压力及WR位置处的波高监测与实验值对比分别见图2和图3。

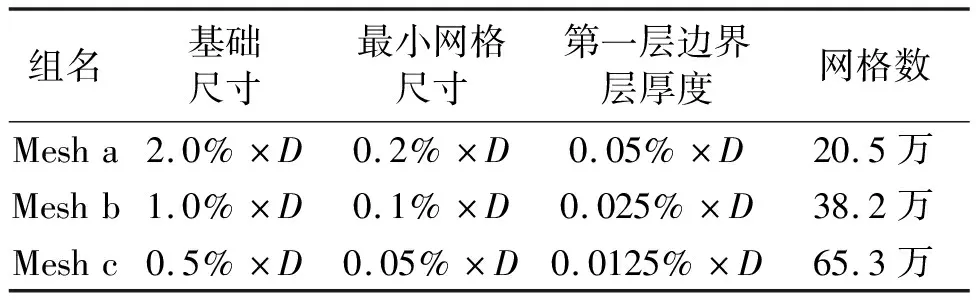
表1 网格划分尺寸

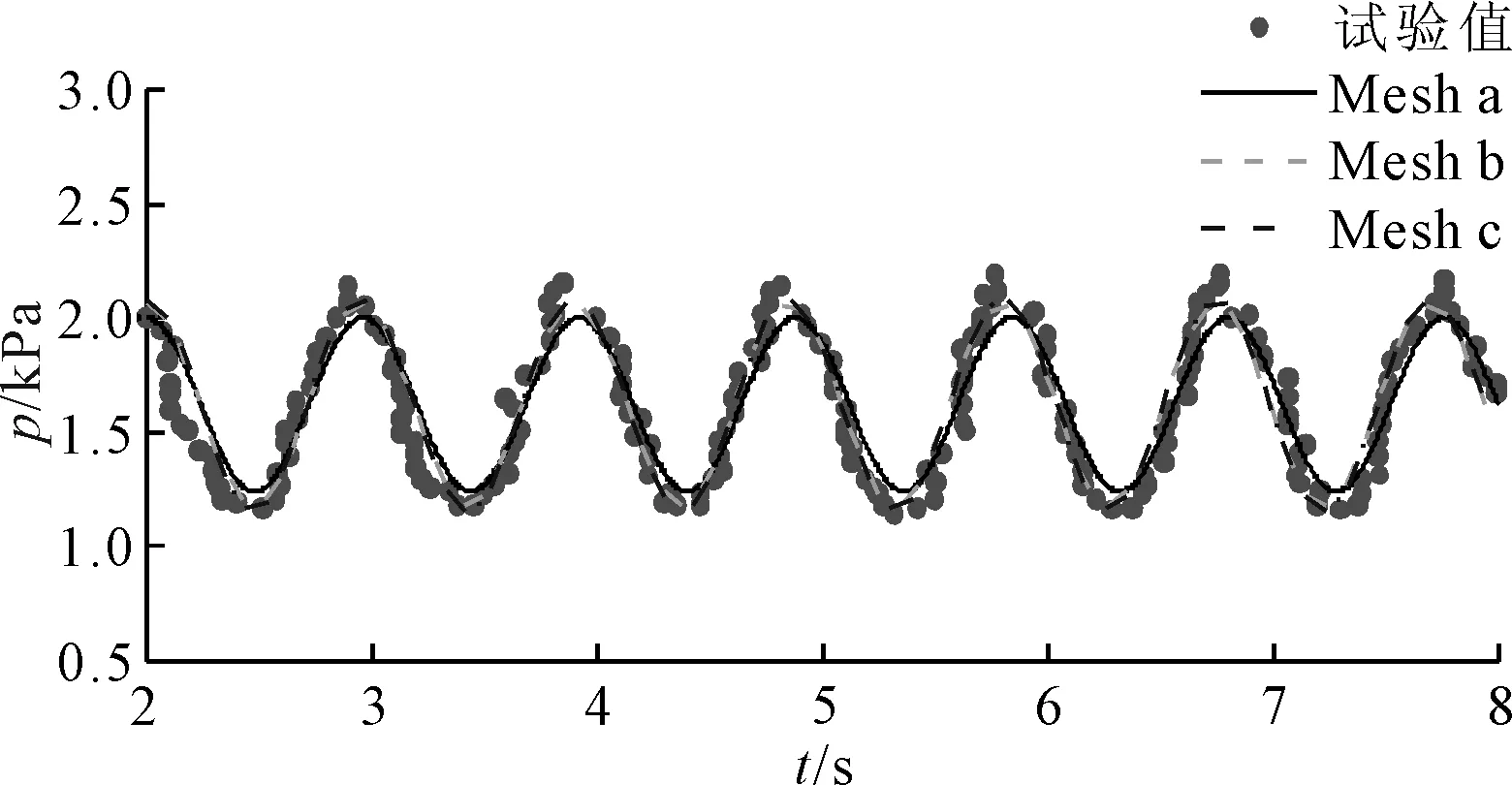
图2 R3点压力时历曲线对比

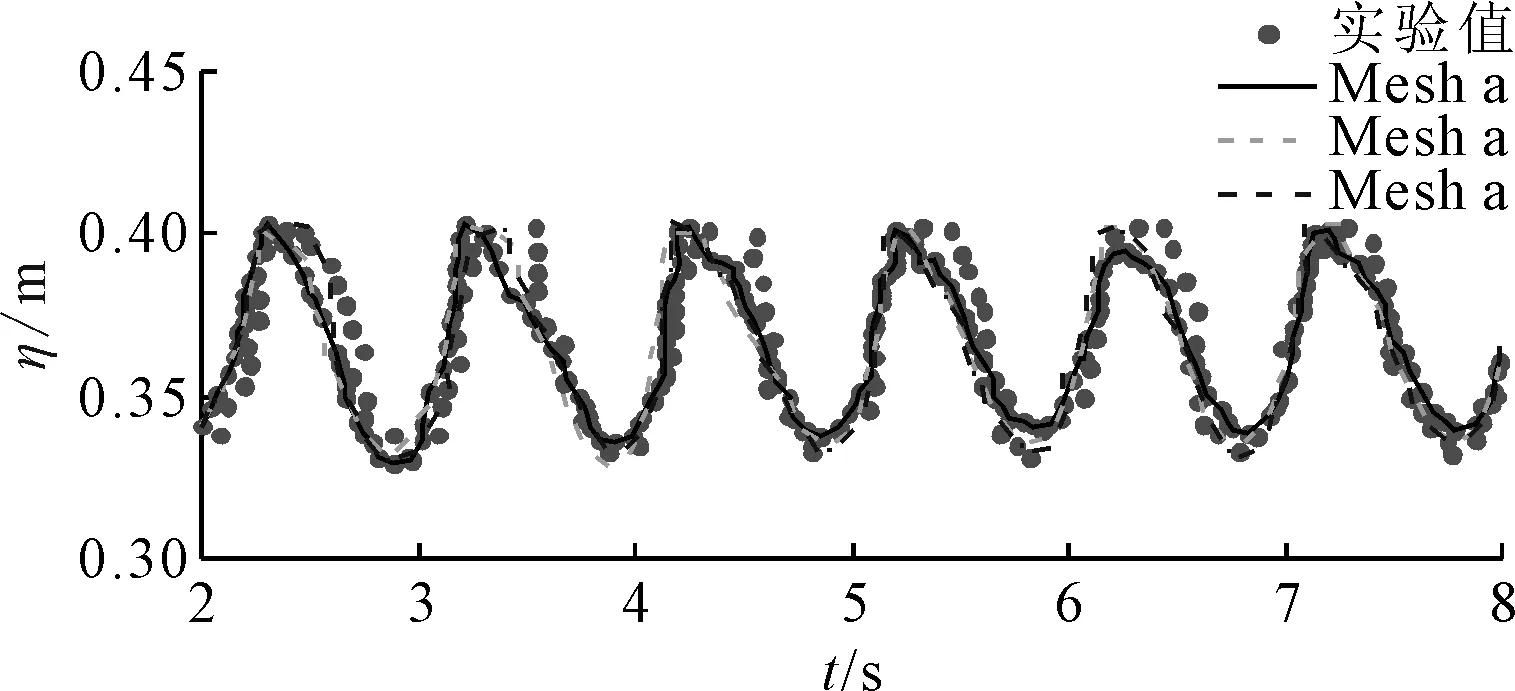
图3 WR位置波面高度时历曲线对比

从图2和图3中可以看出，3组网格计算得到的监测点压力及浪高监测与实验值对比吻合良好，虽然监测点峰值压力与实验结果略有差别，但随着网格加密，数值计算结果与实验值逐步趋近，验证了本文所采用的网格的收敛性。由于所述某10万t级养殖工船液舱形状与实验模型类似，因此后续计算中网格划分采用相同方法进行划分，网格尺度采用Mesh c。

3 计算模型

选取船首、船中2处典型位置养殖舱，见图4。1号液舱关于中纵剖面对称布置，长宽高分别为22.4 m、19.6 m和19.1 m；2号液舱在左舷，长宽高分别与1号液舱相同。所有液舱均装载至距基线16.5 m高度处，液舱底部距船体基线高度均为2.4 m。

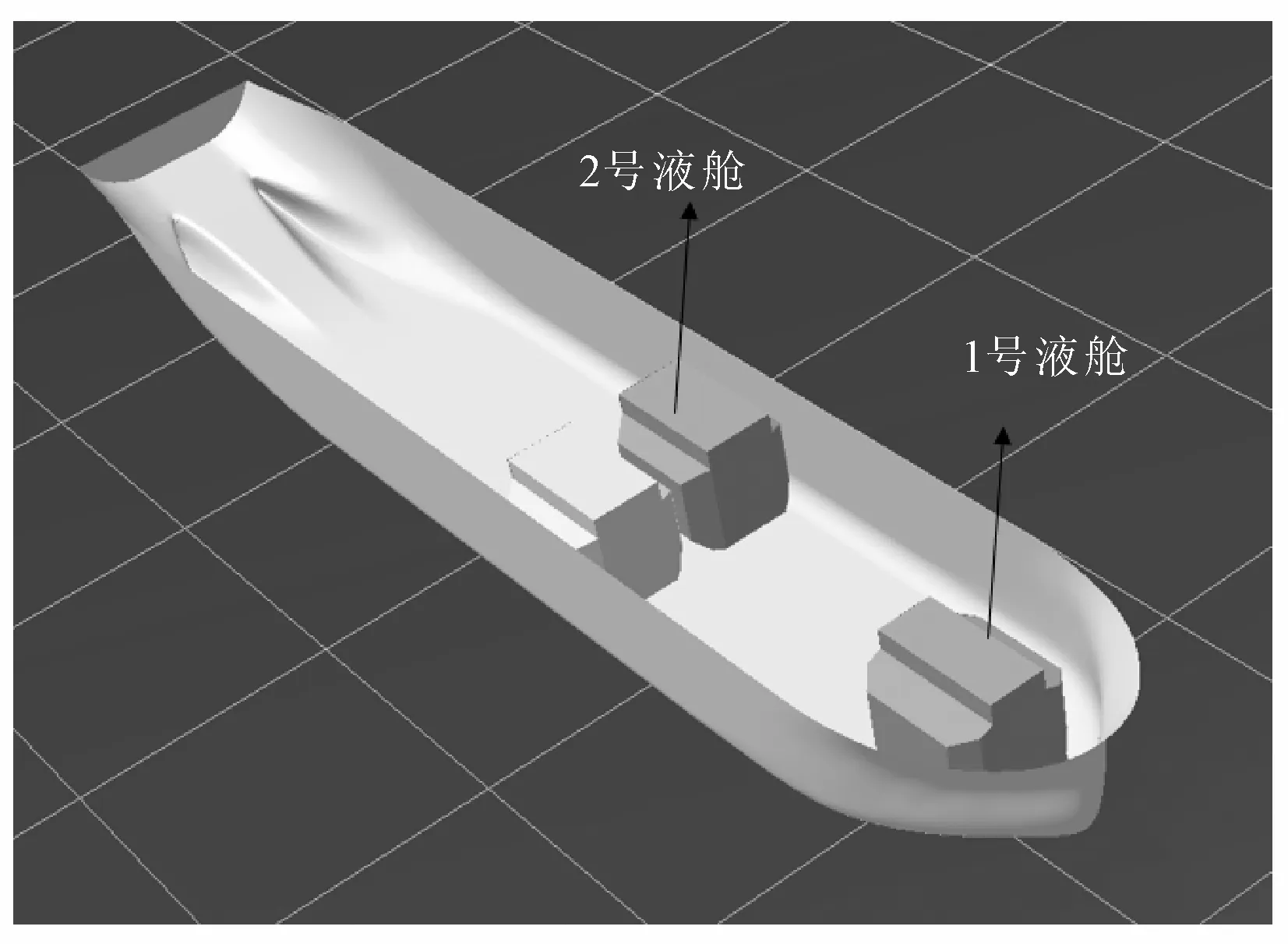
图4 液舱几何模型及布置位置

横摇运动为船舶最主要的运动，因此计算中采用简谐横摇运动作为船体运动输入，船体横摇运动方程为

φ(t)=φ0sin(ω(t-Δt))

(4)

式中：φ为船舶横摇运动角度；φ0为船舶横摇运动幅值；ω=2π/Th，Th为船舶横摇运动的周期；Δt为计算中设置的缓冲时间。船体主尺度参数见表2，选取船体重心位置为横摇中心。

表2 船体主尺度参数 m

液舱网格采用前述Mesh c网格划分方法，在自由液面附近进行网格加密处理，结果见图5。

图5 液舱网格划分结果

选取2个液舱长度中心平面处不同位置处的监测点进行流速监测，监测点位置见图6。

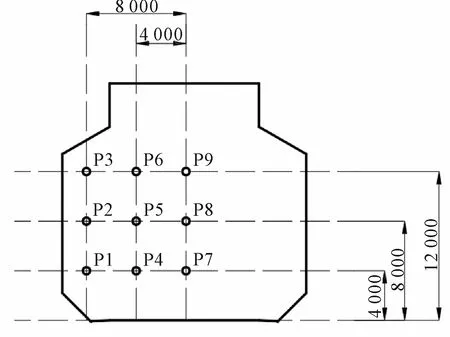
图6 液舱监测点位置

4 结果分析及讨论

4.1 单工况流场

以横摇运动周期7.855 s，横摇幅值5°为例，各液舱不同监测点位置处的流体速度时历曲线见图7。3个液舱的监测点流速整体具备一定的周期性，观察发现3个液舱监测点处流速最大值由1号液舱到2号液舱呈逐渐增大的趋势。2号液舱与1号液舱不同在于2号液舱布置并非沿船中对称，因此舱内液体晃动幅度相对较大。

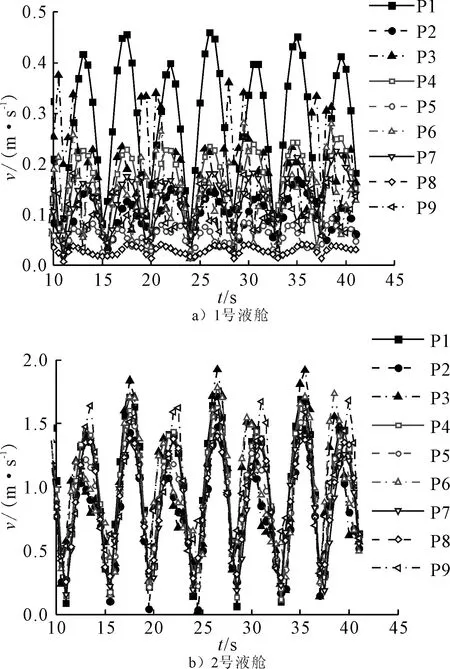
图7 各液舱监测点速度时历曲线

2个液舱受到的横摇力矩时历曲线见图8，从图8可以看出1号液舱由于沿船中对称布置，因此横摇力矩基本为0。而2号液舱布置在船体左舷，因此横摇力矩为负值，力矩大小达到108量级，且呈一定的周期性变化，变化周期与运动周期吻合。

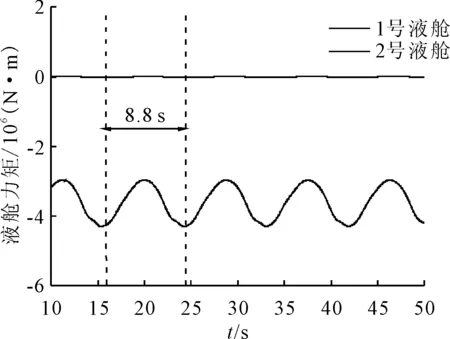
图8 各液舱横摇力矩时历曲线

4.2 不同横摇周期适渔性流速

养殖舱内水体流速对养殖舱的适渔性有重要影响，一般认为鱼类适合养殖的流速范围为

V=(1.19～1.66)L1/2

Vcr1=0.15+2.4L

Vcr2=2.3L0.8

(5)

式中：V为鱼类适养流速的上下限范围；Vcr1和Vcr2为养殖鱼最大游动速度；L为养殖鱼体长。以最常见的大黄鱼为例，体长一般为20 cm，通过上式进行计算，得到适养流速为0.63 m/s。因此，本文以0.6 m/s作为养殖舱适养流速的上限。

同样以横摇运动周期7.855 s，横摇幅值5°为例，液舱内适养流速占比(流速小于等于0.6 m/s)时历曲线见图9。

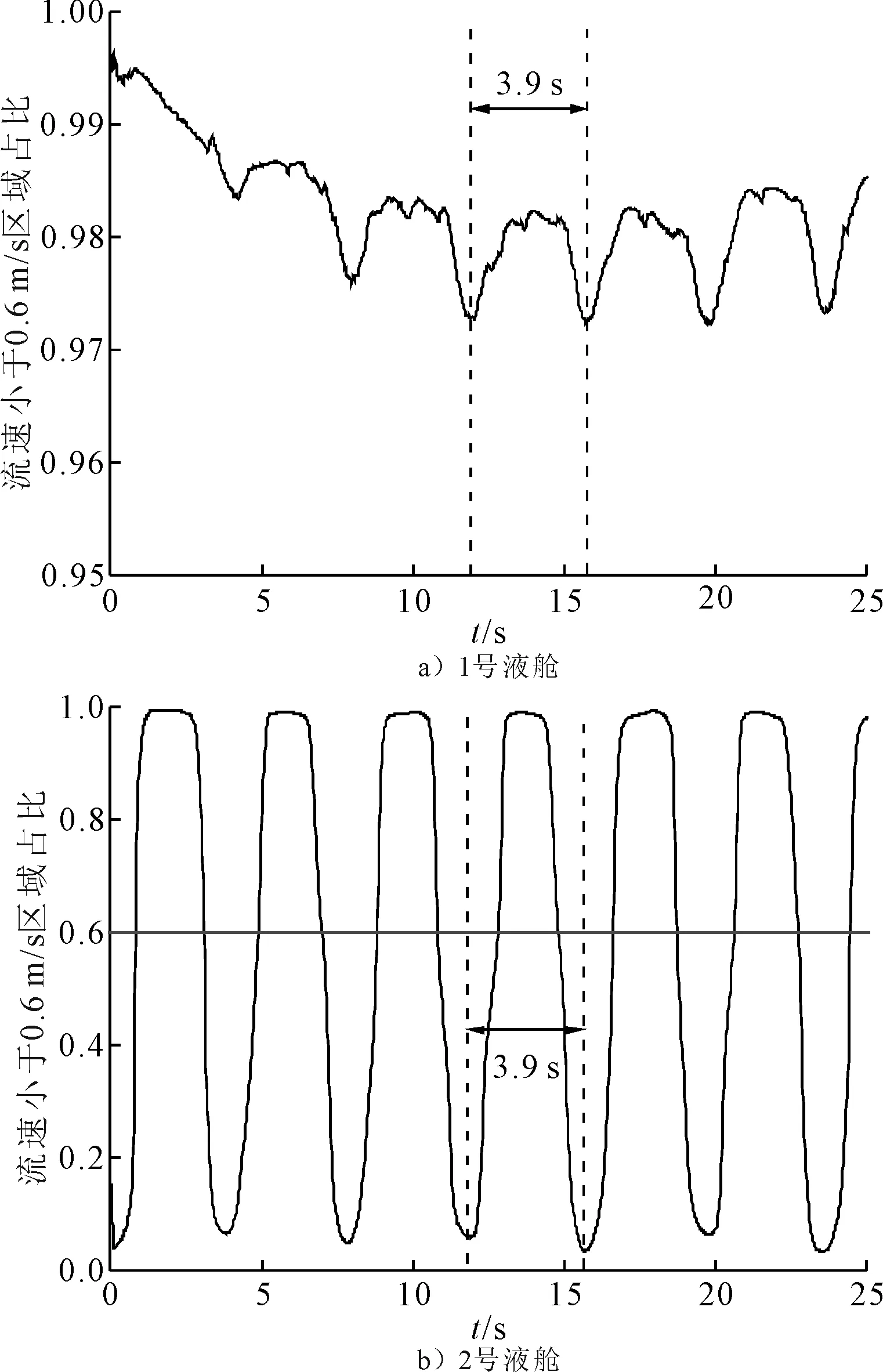
图9 不同液舱适养流速占比时历曲线

由图9可见：不同位置处的液舱适养流速占比曲线均呈现一定的周期性，同时由于液舱晃荡下流体的运动有一定的滞后性，因此在一个横摇运动周期内相同位置处的流场速度变化会重复2次，因此适养流速占比曲线周期为横摇运动周期的一半。1号液舱内适养流速占比均在97%以上，具有良好的适养性。而2号液舱内适养流速占比随时间变化很大，最小为3.6%，最大接近100%，在1个周期内适养流速占比大于60%的时间大约为2 s，在1个曲线周期中的比例约为60%。

对于矩形液舱，其液体固有周期T为

(6)

式中：n为阶数，这里仅计算一阶频率，n=1；L为液舱运动方向自由液面长度，L=19.6 m；H为充液深度,H=14.1 m；g为重力加速度。所述养殖水舱基本构型主干部分为矩形，因此用上述公式计算可能与实际有所偏差，但差别不大，计算得到横摇方向一阶固有周期为5.126 s。因此，重点关注养殖舱固有周期附近范围内横摇周期对养殖舱适渔性的影响。

不同横摇周期下的液舱适养流速区域占比规律类似，采用与图9相同的分析方法总结见表3。可以看出1号液舱的整体适养流速区域占比均在90%以上，这表明养殖舱对称布置，养殖环境更加有利，且1号液舱适养流速区域占比随着横摇周期的增大而增大。2号液舱一个周期内适养流速区域比例超过60%的时间占比随着横摇周期的增大而增大，结合1号液舱结论，可以得出相同横摇幅值时，横摇周期越小，液舱内流体速度变化越剧烈，对养殖环境越不利。同时发现，养殖舱横摇运动周期为5.126 s(横摇固有周期)时，舱内适养流速占比并未出现明显的降低。

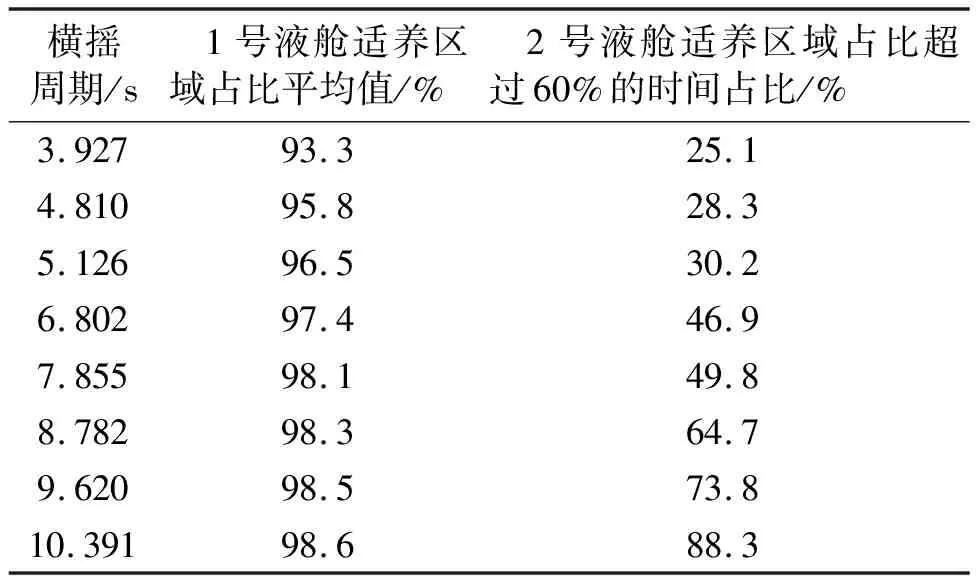
表3 液舱适养流速占比规律

4.3 不同液位高度适渔性流速

以横摇运动周期8.782 s，横摇幅值5°为例，对不同液位高度下养殖舱适渔性流速进行计算。3种液位高度对应距基线的距离分别为14.0 m(液舱肩部以下)、16.5 m(液舱肩部)和19.5 m(液舱肩部以上)，见图10。

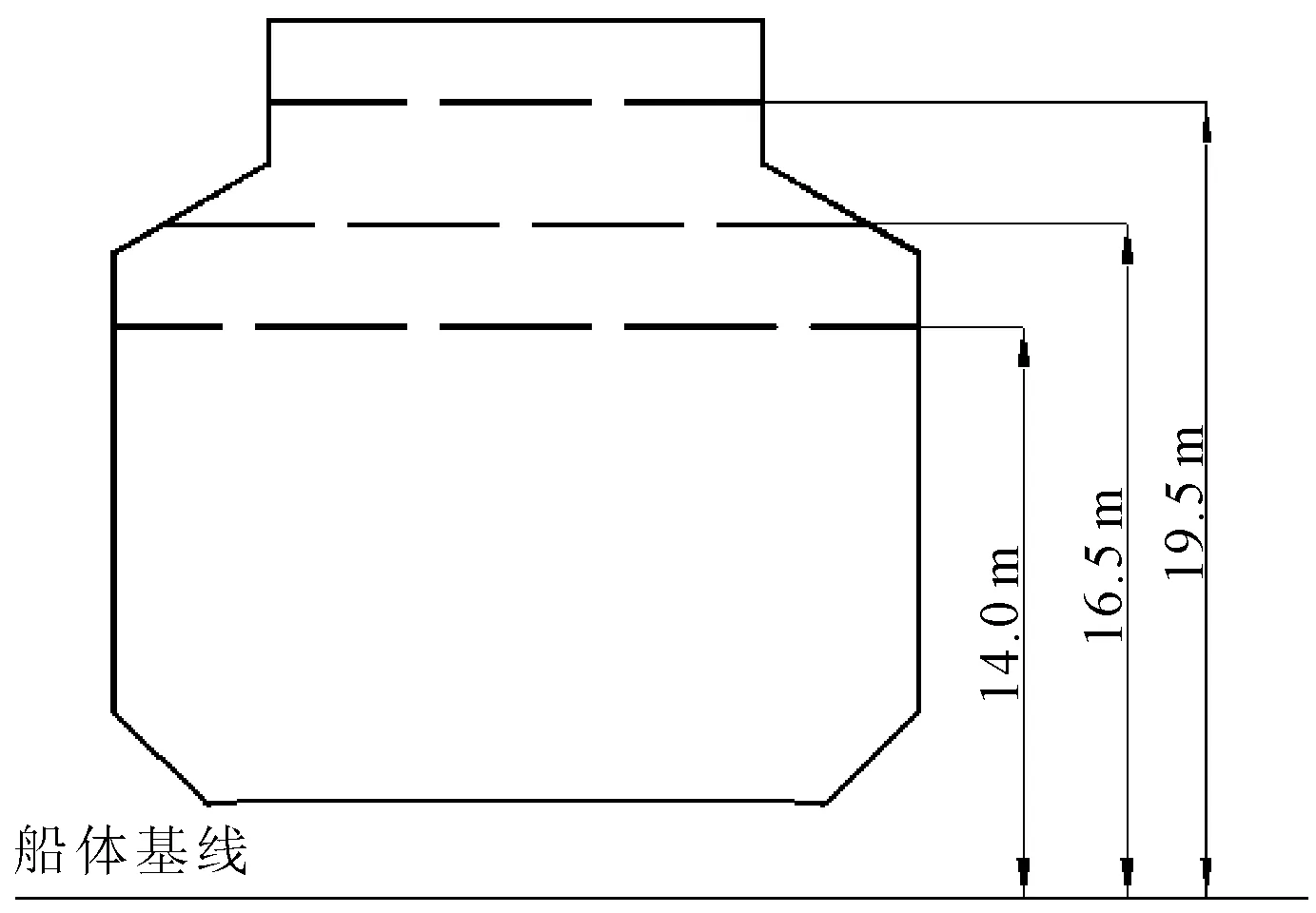
图10 不同液位高度示意

不同液位高度下两液舱流速小于0.6 m/s区域占液舱流体比例时历曲线见图11。

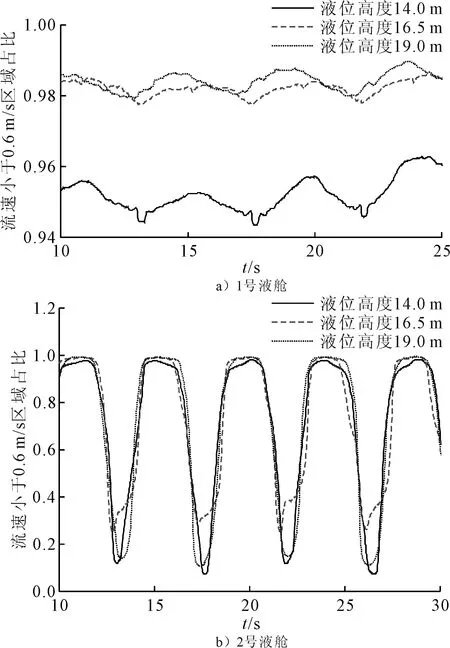
图11 不同液位高度下液舱适养流速占比时历曲线

1号液舱中3种液位高度下，液舱适养区域均在94%以上，且随着液位高度的增大，适养区域占比也有一定增大。

2号液舱适养区域占比规律类似，从表4中可以看出，1个周期内适养区域占比超过60%的时间比例均相差不大。需要注意的是，液位高度为16.5 m时适养区域最小占比高于另外2种装载情况，这表明养殖舱装载位置为肩部区域时液舱内晃荡程度较小。

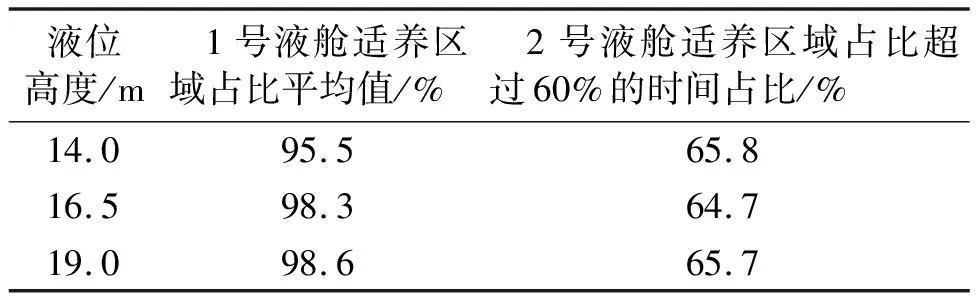
表4 不同液位高度液舱适养流速占比规律

5 结论

1)经过与实验对比，验证了所采用的数值计算模型的准确性，可以有效模拟液舱中的流场特性。

2)养殖舱沿船中对称布置相比左右舷布置可以明显的降低养殖舱内流体的晃荡程度、减小液舱受到的力矩、提高养殖舱适养流速区域占比。

3)液舱适养流速区域占比时历曲线具有一定的周期性，其周期大致为横摇运动周期的一半。横摇幅值相同时，随着横摇周期的增大，养殖舱内流体晃荡程度减缓，养殖舱适养区域占比增大。

4)对于沿船中对称布置的液舱，随着养殖舱液位高度的增大，养殖舱适养区域占比也随之增大。对于沿船体左右舷布置的液舱，养殖舱液位的高度对适养区域占比影响较小，但养殖舱装载位置在肩部区域时，舱内流体整体晃荡程度较小，是比较适宜的装载高度。