悬臂式抗滑桩三维土拱效应及桩间微桩加固作用机制研究

黄达 冯开 宋宜祥

摘要 揭示悬臂式抗滑桩间土拱效应的空间分布，有助于桩间距设计及桩间土稳定性控制等技术的发展。采用有限元分析数值模拟方法，通过对悬臂桩后土体的应力及位移进行分析，得到了土拱的三维空间形态及其影响因素。在此基础上，对桩后土体水平方向应力突变峰值点数据进行统计分析，得到了不同桩间距条件下的土拱轴线方程。通过土拱的轴线方程可以判断自然土拱的位置，在桩间自然土拱不同位置布置微桩群，研究微桩布置在不同区域对桩间土稳定性的影响，探究微桩最佳布置区域。同时探索微桩尺寸、弹性模量对其桩间土加固效果的影响规律。

关 键 词 悬臂式抗滑桩;土拱效应;微桩 ;桩间距;桩间土

中图分类号 TU473     文献标志码 A

Abstract To reveal the spatial distribution of soil arch effect between cantilevered anti-slide piles is helpful to the development of pile spacing design and soil stability control between piles. By means of finite element analysis and numerical simulation， the stress and displacement of the soil behind the cantilever pile are analyzed， and the three-dimensional space shape of the soil arch and its influencing factors are obtained. Based on it， the peak point data of abrupt stress in horizontal direction of soil behind piles are statistically analyzed， and the soil arch axis equation under different pile spacing conditions is obtained. The position of the natural soil arch can be judged by the axis equation of the soil arch， and the pile groups are arranged at different positions of the natural soil arch between piles， so as to study the influence of the micro-pile arrangement in different areas on the stability of the soil between piles and explore the optimal area of micro-pile arrangement. At the same time， the influence law of micro-pile size and elastic modulus on the reinforcing effect of soil between piles is explored.

Key words cantilever anti-slide pile; soil arch effect; micro pile; pile distance; soil between piles

0 引言

Terzaghi于1943年通过活动门试验，证实了土力学领域土拱效应的存在[1]。当土体运动时，可在悬臂桩间产生“土拱效应”，土拱将桩后土体所承受的力转移到桩体上，这种应力转移现象有利于桩间土体的稳定，因此研究悬臂桩的土拱效应对于工程实践具有重要意义。

由于桩孔及桩前切坡施工扰动等影响，悬臂式抗滑桩土拱效应很难在工程实践中精准观测，数值模拟方法在这方面具有较好的优势。采用有限差分法：Chen等[2]将桩的荷载-位移曲线和拱效应联系起来，解释了应力是如何从土中传递到桩上的;林治平等[3]对比分析了抗滑桩结构工程中摩擦拱、端承拱和联合拱三类土拱效应。采用有限元法：董捷等[4]对比了悬臂式抗滑桩三维与二维数值模拟土拱效应的差异性;吕庆等[5]研究了桩周土应力及变形等演化规律。采用离散元法：向先超等[6]研究了土拱效应的形成、发展、破坏和再形成过程;王桂林等[7]提出了结合相对位移和最大主应力等值线综合确定了土拱厚度的方法。

同时，越来越多的学者将土拱效应应用到了抗滑桩设计当中。Li等[8]通过研究相邻稳定桩之间的土拱效应，推导了考虑滑体重力和抗剪强度以及桩截面尺寸的合理稳定桩间距模型。He等[9]讨论了桩土各类影响因素在滑坡稳定桩设计中的最优组合。Wu等[10]基于对相邻稳定桩间土体摩擦拱的力学分析，提出了一种等腰梯形截面横向受荷稳定桩的通用力学模型。Lei等[11]通過对斜坡在不同桩间距条件下进行离心试验，探讨了桩间距对土拱破坏位置的影响。不少学者对微桩的边坡加固机理也做了许多研究。陈正等[12]对现场柔性微型桩试验进行有限元数值模拟，分析了微桩各个参数对其水平承载力的影响，给出了桩长、桩径、桩身弹性模量的合理取值。刘续[13]对微桩等效土体法和微桩抗剪强度法进行理论分析，探讨了注浆微桩加固边坡的计算方法。Mujah等[14]研究了不同地基密度下，在砂土中引入多排微桩的效果。Deng等[15]分析了微桩在边坡稳定性分析中的受力机理，推导出了有效微桩侧压力的计算公式。Zeng等[16]根据运动极限分析的上界定理，提出了在给定安全系数的情况下，以微桩群和桩坡滑动面计算微桩群的净推力的解析方法。

目前对于微桩加固悬臂桩桩间土的研究还不够全面，特别是结合土拱效应进行支护设计方面有待进一步研究。因此，本文采用有限元数值模拟方法，对悬臂桩土拱效应的三维空间形态及其影响因素进行研究，并通过对土体不同位置水平方向土压力突变峰值点位置的统计，拟合获得了土拱轴线方程，初步探讨了在土拱区域布置微桩群提高桩间土稳定的有效性。

1 数值试验方案

1.1 几何模型及本构模型

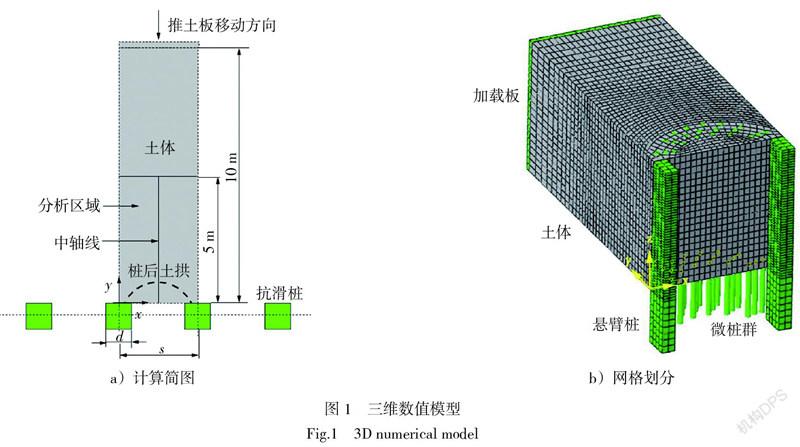
悬臂式抗滑桩布置具有对称性， 故取两根桩及其中心范围内土体进行模拟，见图1。d为抗滑桩宽度，s为桩中心距，桩后计算域取10d。

根据董捷建议的推桩试验可模拟悬臂桩支挡作用机理[17]，故本文采用平推桩后土体模拟边坡土体运动及受力情况。利用有限元软件Abaqus，悬臂桩、加载板采用线弹性实体单元模型，微桩采用梁单元，土体为Mohr-Coulomb弹塑性实体单元模型。桩土接触界面为库仑摩擦模型，微桩与土体之间采用嵌入约束，土体与桩及加载板间的摩擦系数取0.3。如图1所示，近桩区域与远桩区域之间中间设置网格过渡，实体单元类型网格为C3D8，梁单元网格为B31。由于滑面以上的土拱对桩体的作用最有意义[18]，故桩后仅模拟滑面以上土体（土体底部表面假定为滑动面）。

1.2 边界条件

土体底部采用竖直z方向位移约束，模型左右两侧采用x方向位移约束，悬臂桩、微桩滑面以下嵌入岩体段采用固定约束。模型顶面、桩间土表面及桩体悬臂段均自由表面。为了获得悬臂桩后土拱的形成过程，通过对加载板施加位移速率（16 mm/0.02分析步）挤推土体向临空方向运动。

1.3 模拟方案及计算参数

1.3.1 土拱效应模拟方案

研究悬臂桩土拱效应时，桩的截面尺寸和桩间距对土拱效应的影响较大[19]，地质灾害防治工程设计规范[20]指出：桩间距s取3d到5d时，桩间土会产生拱效应，考虑其建议，基本算例采用方桩宽度d = 1 m，桩中心距s = 3d。桩高h = 7 m，悬臂段5 m，嵌固段2 m。土体尺寸：长×宽×深为10 m×3 m×5 m。加载板尺寸：长×宽×高为0.2 m × 3 m × 5 m。土体采用黏性土，材料属性见表1。

为了定量分析桩间距、加载板位移对桩间土拱的影响，制定了两类共9组试验，方案如表2所示。

1.3.2 微桩加固桩间土模拟方案

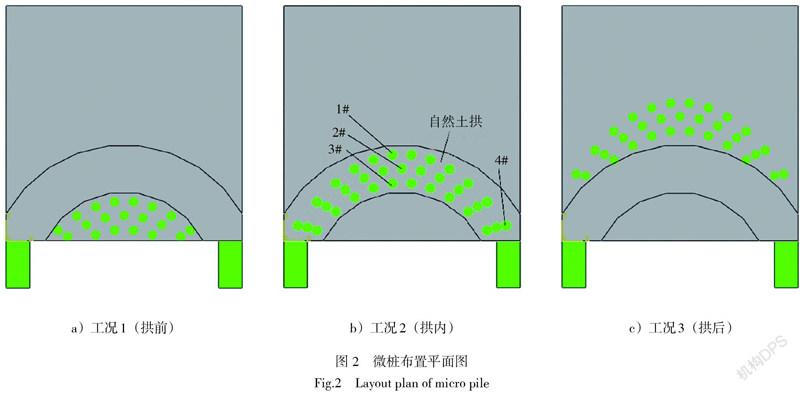
微桩一般指桩径70～300 mm的钻孔灌注桩，长细比通常大于30，实际工程中往往把微桩群作为一个整体结构，将其当作柔性挡墙[21]。为研究微桩群对桩间土体稳定性的影响，在桩间距为5d的模型中，沿土拱轴线布3排微桩，微桩水平向间距取L = 400 mm，排间距取T = 300 mm。微桩直径D = 200 mm，微桩高H = 7 m，嵌入土体段5 m，嵌入岩体段2 m。其他参数同土拱模拟方案。为了进一步研究布桩位置对桩间土稳定性的影响，本文试图在桩间土拱前方、内部及后方布置微桩群并对微桩群内土体进行注浆加固。3种布置工况如图2所示，微桩群的加固宽度小于土拱厚度。

为了分析布桩位置、微桩尺寸、弹性模量、悬臂桩桩间距对桩间土加固效果的影响，制定了4类共9组试验。方案如表3所示。

2 悬臂桩土拱三维形态及拱轴线方程拟合

2.1 土拱三维形态的确定方法

土拱是一种拱形结构，土拱范围内的土体应力会发生一定程度的突变，本质上是将作用在其上的土压力转化为轴力，最终传递至拱脚[22]。土拱效应越强，土拱上土颗粒间的楔紧效应就越明显，此处土体间挤压力必将高于同一高度周边土体[23]。因此，本文通过土压力的突变情况来确定土拱的形态。

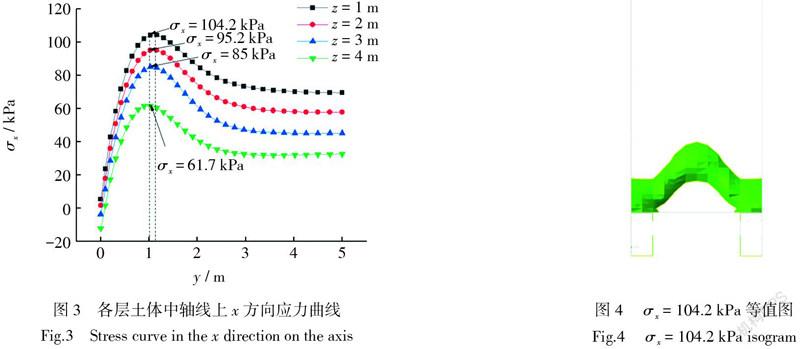
由张永兴等人的研究可知，土体x方向应力突变峰值点为土拱轴线跨中位置的顶点[23]，其y向坐标就是土拱的矢高。提取各层土体中轴线上土体x 方向应力曲线，由图3可知，桩土相对位移前，受自重影响，土体x方向应力值随土体埋深增大而增大，当加载板推动土体移动时，桩土产生相对位移，远离悬臂桩处，土体x方向应力基本保持不变，靠近悬臂桩后一定范围，各层土体x方向应力值都会发生突变，并在桩后约1.16 m处达到突变峰值。同时可以看到，x向應力等值土拱的矢高沿土体埋深方向不是完全等高的，上部较小，下部较大。土拱范围内，由于土拱的阻挡作用，拱前土体的应力迅速下降，在靠近桩后的位置则变得很小，仅是峰值的23%，这表明应力由土体转移到了桩身，并形成以悬臂桩背三角形受压区[18]为拱脚的x方向应力等值拱，如图4所示。

图5为各层土体中轴线上x方向应力峰值的等值面，从中可以清楚看到，x方向应力等值拱具有上部薄，下部厚的空间特征，且小等值拱包络在大等值拱内部。土体截面越高，中轴线上x方向应力的突变峰值越小，拱高越大，这表明x方向应力等值拱的拱高与土体截面高度呈负相关关系。各层土体x方向应力值的突变程度分别为34.71%，37.55%，39.79%，29.14%，故土拱效应在土体的中下部较强。

王桂林等[7]提出，土拱拱厚可以通过分析桩后土体最大主应力和位移分布得到。分析桩后y = 0.42 m、0.65 m、0.9 m、1.16 m、1.44 m、1.74 m、2.06 m截面最大主应力和位移分布。由图6可知，桩后0.65 m到1.74 m土体最大主应力近似相同，可以看出土拱的厚度约为1 m。同时，土拱产生后会对桩后土体的运动造成阻碍作用，土拱区域土体的位移值也应该比较接近，由图7可知，桩后0.65 m到1.74 m范围内土体的位移基本相同，这一结论与图6所得基本一致。

2.2 土拱矢高的变化规律

x方向应力峰值点的y坐标是土拱的矢高。由图8可知，加载板位移80 mm到480 mm时，土拱处于形成阶段，矢高会随加载板位移增大而逐渐增大，加载板位移到达560 mm时，土拱趋于稳定，矢高不再发生明显变化，由此看出，土拱形成过程中，矢高是不断变化的。

如图9所示，土拱矢高随桩间距线性增大，桩间距是影响土拱矢高最主要的因素，但当桩间距过大时，悬臂桩桩间土体容易失稳，发生塌落，此时就需要对桩间土体进行加固支护。

2.3 土拱拱轴线的拟合

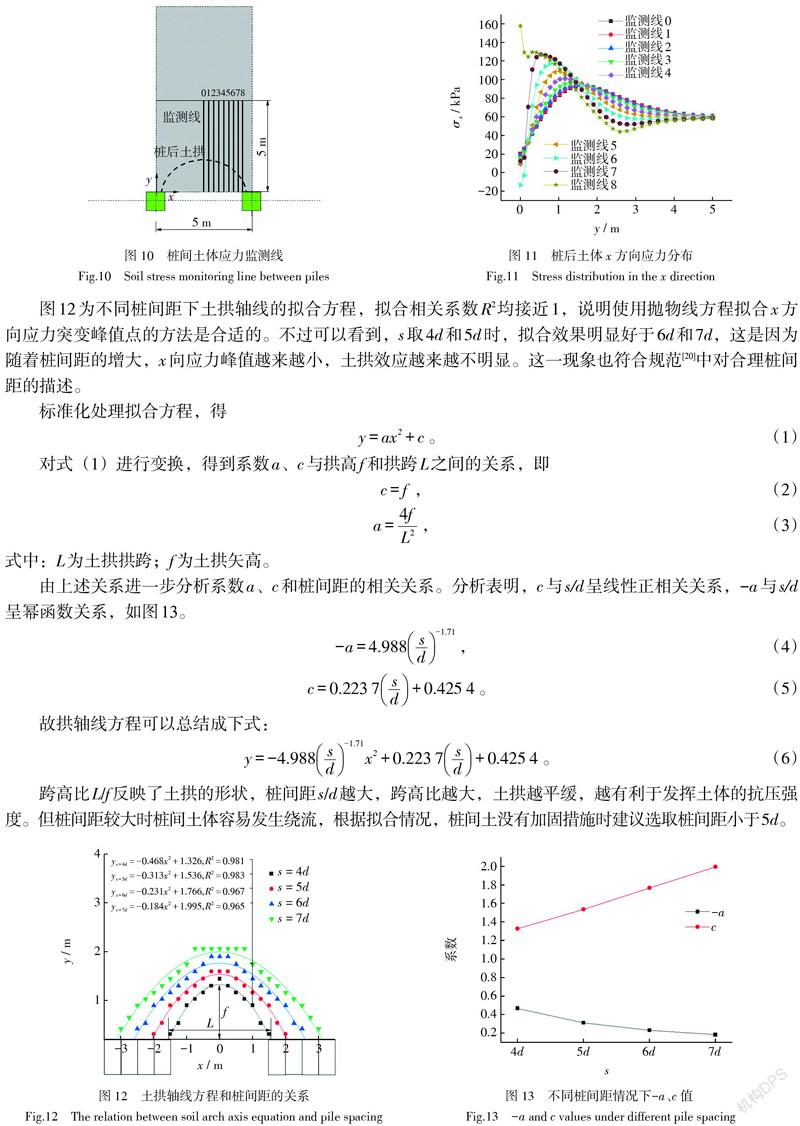
土拱土颗粒相互“楔紧”时，土体x方向应力会发生突变，不难得出，x方向应力突变的峰值应该均处于土拱轴线上。通过在土体z=1 m高度截面上设置一系列监测线（图10），来捕捉桩间土体不同位置竖向剖面上的x方向应力峰值点，并对其按照抛物线方程[24]进行数据拟合。由于拱型结构的对称性，监测线设置半跨即可。

图11为s = 5d时，各条土体应力监测线上x方向的应力分布，突变峰值点的y向坐标由跨中向桩体方向逐渐减小，这符合图10中的理想分布。

图12为不同桩间距下土拱轴线的拟合方程，拟合相关系数R2均接近1，说明使用抛物线方程拟合x方向应力突变峰值点的方法是合适的。不过可以看到，s取4d和5d时，拟合效果明显好于6d和7d，这是因为随着桩间距的增大，x向应力峰值越来越小，土拱效应越来越不明显。这一现象也符合规范[20]中对合理桩间距的描述。

由上述关系进一步分析系数a、c和桩间距的相关关系。分析表明，c与s/d呈线性正相关关系，-a与s/d呈幂函数关系，如图13。

跨高比L/f反映了土拱的形状，桩间距s/d越大，跨高比越大，土拱越平缓，越有利于发挥土体的抗压强度。但桩间距较大时桩间土体容易发生绕流，根据拟合情况，桩间土没有加固措施时建议选取桩间距小于5d。

3 微桩群加固桩间土稳定性分析

3.1 微桩群位置对桩间土稳定性的影响

分析微桩加固桩间土模拟方案数据，对推土板均施加320 mm位移。如图14所示，监测土体临空面上沿深度方向跨中各点的y向位移，并以此作为衡量土体稳定性的指标。

由图15可知，微桩布置于自然土拱不同区域，临空面土体沿深度方向的位移均呈下降趋势。土体截面高度z = 1 m和5 m处，微桩位于拱内时，位移减小幅度均最大。即同一高度，相比拱前和拱后，微桩布置在土拱区域内部时，临空面土体位移最小，桩间土加固效果最好。插入微桩后，土体下部位移减小幅度明显大于上部，这是因为微桩下部嵌固于岩体之中，与注浆土体形成稳定的拱形结构，对桩间土体的加固效果明显，微桩上部自由度较高，会随着土体的运动而发生屈曲，因此加固效果不明显。

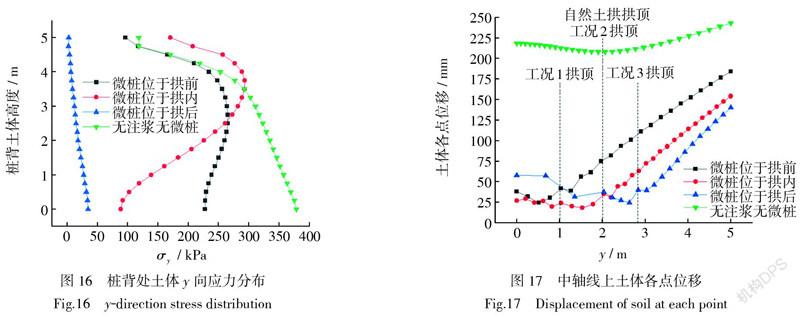
桩背处土体y向应力反映了土拱传向悬臂桩力的大小。由图16可知，微桩布置于拱后时，土拱区域受到注浆土体和微桩群的阻挡作用，桩土间不再发生相对位移，很难产生土拱效应，因此传递到悬臂桩背的力也很小，此时加载板推力主要由微桩和注浆土体承担。微桩布置于拱内时，土体下部由于微桩嵌入岩石，嵌固端固定，阻碍了桩间土体移动，土拱效应不明显，故桩背土体y向应力较小。而桩背土体高度z = 3.75 m处y向应力最大，这是由于上部微桩自由度高，对土体阻挡效果弱，土体仍会与悬臂桩桩产生相对位移，在微桩与注浆作用下，一定程度增强了此处的土拱效应。微桩布置于拱前时，布桩位置的土体稳定性增强，但这减少了桩土间的相对移动，导致土拱效应减弱，桩背处土土体y向应力比无微桩时小。

综上所述，土拱内部是微桩的最佳布置位置。布置微桩的最终目的是提高桩间土体的稳定性和整体性，微桩群虽然影响了桩后土体的自然土拱，但极大提高了桩间土体的稳定性，因此微桩加固桩间土的设计思路是有效的。

图17为土体高度z = 1 m时中轴线上各点的位移情况。可以看到，微桩群的加固作用非常明显，布置微桩后土体的整体位移大幅度减小。土体中有土拱时，由于土拱的挡土作用，土体位移在拱顶处产生拐点，由此可以判断土体中土拱的位置。当微桩布置在自然土拱内部时，形成的土拱位置与自然土拱基本一致。布置于拱前时，微桩群的存在导致自然土拱的形成受到影响，故自然土拱拐点不明显。布置于自然土拱之后时，微桩群挡土作用显著，自然土拱基本不再产生。因此，微桩群加固桩间土的效果很强，布置于不同位置时对土体中的自然土拱会产生不同影响，为了最大程度提高桩后土体的整体性，微桩群最好布置在自然土拱内部。

3.2 微桩直径尺寸对桩间土稳定性的影响

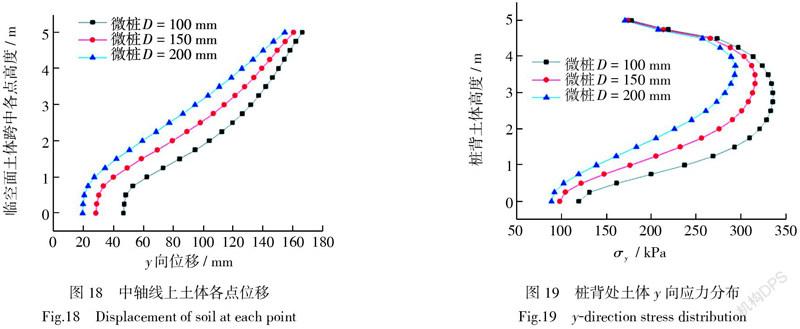
由图18可知，不同微桩直径尺寸下，桩后土体位移减小趋势一致，微桩直径越大，擋土效果越好，微桩直径尺寸与其对土体稳定性的提升呈正相关关系。微桩直径越大，相同加载板位移下，土体的运动越受限，土拱效应的产生条件减弱，土拱效应越弱，但同时土体受到的扰动越小，整体性越强。由图19可知，土体y向压应力的最大值出现在不同高度截面，微桩尺寸越大，最大值的出现位置越高，土拱效应最强的位置越靠近土体上部。因此布置微桩时，在成本允许范围内，应尽可能选择尺寸较大的微桩。

3.3 微桩弹性模量对桩间土稳定性的影响

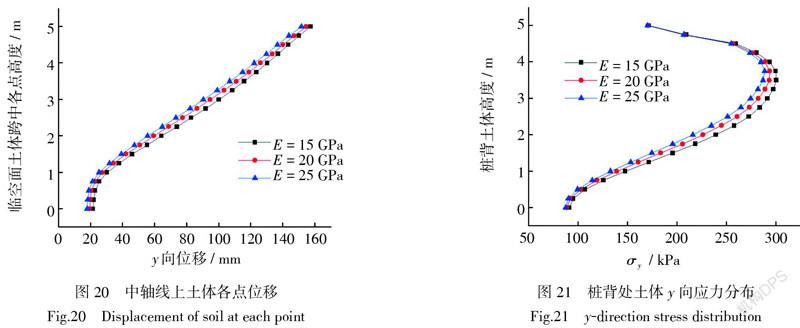
由图20所示，微桩弹性模量越大，桩后土体各高度截面位移越小，微桩群对桩间土体稳定性的提高越大，但同一土体截面高度，微桩弹性模量不同时，土体位移平均相差3 mm，这表明微桩弹性模量对注浆微桩拱的加固作用贡献非常小。

如图21所示，微桩弹性模量越大，桩后土体桩背处土压力越小，但差别很小。综上所述，微桩弹性模量不是设计注浆微桩拱的重要考虑因素，在保证设计安全的基础上正常取值即可。

3.4 悬臂桩间距对人工土拱加固作用的影响

实际工程中，桩间距不宜设计过大，否则桩间土体容易失稳，但桩间距过小，所需抗滑桩的数量就会增大，抗滑桩造价昂贵，容易造成经济浪费，因此设置桩间微桩群不仅可以提高桩间土体稳定性，最重要的是能够在一定程度上让扩大桩间距成为一种可能，从而节约成本。

由图22可以看出，桩间距越大，相同加载板位移作用下，桩后土体位移越大。微桩在桩间距为4d，5d，6d情况下均可以提高桩间土体的稳定性，桩间距越大，微桩群作用下桩后土体位移减小量越大，土体加固作用越明显，这表明布置于土拱区域内部的微桩群，可以有效提高桩间土体整体性，且桩间距越大，加固效果越好，这为扩大悬臂桩桩间距提供了可能。

3.5 微桩加固桩间土的作用机制

自然土拱作用时，桩后土体各个高度截面上，土体x向应力等值面均呈拱形分布，由于相邻土拱拱脚处重叠，形成三角形受压区，故拱脚处土压力最大。由图23可知，微桩作用时，情况有所不同：土体z=1 m处，土拱处x向应力等值图不再呈拱形分布，自然土拱效应微弱，x向应力最大值出现在人工土拱拱顶处，而且作为拱腳，与相邻人工土拱之间形成了新的土拱;土体z=4 m时，自然土拱效应明显，由于微桩和注浆土体的加固作用，土拱强度得到一定增强。

综上所述，可以得到微桩加固桩间土的作用机制：土体下部，注浆土体和微桩形成的拱形复合结构依靠挡土作用加固桩间土，加固效果显著，桩间土体与桩后土体不再发生相对位移，自然土拱效应微弱，拱形复合结构拱顶作为新的拱脚，与相邻的桩土复合结构之间形成了新的土拱并发挥挡土作用。土体上部，复合结构挡土作用弱于下部，微桩的“加筋”作用提高了自然土拱区域的整体性，土体强度得到提升，自然土拱效应增强，传递到悬臂桩背的土压力力变大。可以看出，微桩加固桩间土的机制类似生活中的拱桥，先有拱，后有力。而土体自发形成的土拱，是土体间不均匀位移产生剪应力来抵抗外力的结果，先有力，后有拱，拱形最有利于受力。因此，在设计边坡悬臂桩时，微桩布桩形式可以借鉴土拱的形态，从而达到较好的抗滑效果。

4 结论

1）土拱产生时， x方向应力等值拱具有上部薄，下部厚的空间特征，且小等值拱包络在大等值拱内部。矢高上部较小，下部较大，且随桩间距线性增大，桩间距是影响土拱矢高最主要的因素。拱高与土体截面高度呈负相关关系。

2）通过对桩间土体不同位置竖向剖面上的x方向应力峰值点按照抛物线方程进行数据拟合可以得到合理的拱轴线方程，c与s/d呈线性正相关关系，-a与s/d呈幂函数关系，桩间土没有加固措施时建议选取桩间距小于5d。

3）微桩布置在土拱区域内部时，桩间土加固效果最好。微桩尺寸与其对土体稳定性的提升呈正相关关系，微桩弹性模量对桩间土的加固效果影响不明显。悬臂桩桩间距越大，微桩的加固效果越好。在设计边坡悬臂桩时，微桩布桩形式可以借鉴土拱的形态，从而加固桩间土。

参考文献：

[1]    KARL T. Theoretical soil mechanics[M]. Hoboken，NJ，USA：John Wiley & Sons Inc，1943.

[2]    CHEN C Y，MARTIN G R. Soil-structure interaction for landslide stabilizing piles[J]. Computers and Geotechnics，2002，29（5）：363-386.

[3]    林治平，刘祚秋，商秋婷. 抗滑桩结构土拱的分拆与联合研究[J]. 岩土力学，2012，33（10）：3109-3114.

[4]    董捷，张永兴，文海家，等. 悬臂式抗滑桩三维土拱效应研究[J]. 工程勘察，2009，37（3）：5-10，30.

[5]    吕庆，孙红月，尚岳全. 抗滑桩桩后土拱效应的作用机理及发育规律[J]. 水利学报，2010，41（4）：471-476.

[6]    向先超，张华，蒋国盛，等. 基于颗粒流的抗滑桩土拱效应研究[J]. 岩土工程学报，2011，33（3）：386-391.

[7]    王桂林，冉龙宝，张亮. 桩间三维土拱效应颗粒流数值模拟及其演化规律[J]. 土木与环境工程学报（中英文），2019，41（5）：1-8.

[8]    LI C D，WU J J，TANG H M，et al. A novel optimal plane arrangement of stabilizing piles based on soil arching effect and stability limit for 3D colluvial landslides[J]. Engineering Geology，2015，195：236-247.

[9]    HE G F，LI Z G，YUAN Y，et al. Optimization analysis of the factors affecting the soil arching effect between landslide stabilizing piles[J]. Natural Resource Modeling，2018，31（2）：e12148.

[10]  WU J J，LI C D，LIU Q T，et al. Optimal isosceles trapezoid cross section of laterally loaded piles based on friction soil arching[J]. KSCE Journal of Civil Engineering，2017，21（7）：2655-2664.

[11]  LEI G，USAI S，WU W. Centrifuge Study of Soil Arching in Slope Reinforced by Piles[C]// WU W. Recent Advances in Geotechnical Research. Springer Series in Geomechanics and Geoengineering. Springer，Cham. 2019：105-115.

[12]  陈正，梅岭，梅国雄. 柔性微型桩水平承载力数值模拟[J]. 岩土力学，2011，32（7）：2219-2224.

[13]  刘续. 注漿微型桩加固边坡计算方法探讨[J]. 工程建设与设计，2015（1）：69-71，74.

[14]  MUJAH D，HAZARIKA H，WATANABE N，et al. Soil arching effect in sand reinforced with micropiles under lateral load[J]. Soil Mechanics and Foundation Engineering，2016，53（3）：152-157.

[15]  DENG D P，LI L，ZHAO L H. Limit-equilibrium method for reinforced slope stability and optimum design of antislide micropile parameters[J]. International Journal of Geomechanics，2017，17（2）：06016019.

[16]  ZENG J X，XIAO S G. A simplified analytical method for stabilizing micropile groups in slope engineering[J]. International Journal of Civil Engineering，2020，18（2）：199-214.

[17]  董捷. 悬臂桩三维土拱效应及嵌固段地基反力研究[D]. 重庆：重庆大学，2009.

[18]  周德培，肖世国，夏雄. 边坡工程中抗滑桩合理桩间距的探讨[J]. 岩土工程学报，2004，26（1）：132-135.

[19]  周应华，周德培，冯君. 推力桩桩间土拱几何力学特性及桩间距的确定[J]. 岩土力学，2006，27（3）：455-457，462.

[20]  DBJ50/T-029—2019，地质灾害防治工程设计标准[S].

[21]  辛建平，郑颖人，唐晓松. 基于弹塑性模型的微型抗滑桩破坏机制研究[J]. 岩石力学与工程学报，2014，33（S2）：4113-4121.

[22]  贾海莉，王成华，李江洪. 关于土拱效应的几个问题[J]. 西南交通大学学报，2003，38（4）：398-402.

[23]  张永兴，董捷，黄治云. 合理间距条件悬臂式抗滑桩三维土拱效应试验研究[J]. 岩土工程学报，2009，31（12）：1874-1881.

[24]  蒋良潍，黄润秋，蒋忠信. 黏性土桩间土拱效应计算与桩间距分析[J]. 岩土力学，2006，27（3）：445-450.