冻融RC梁抗震性能与数值模拟方法

郑山锁 杨路 姬金铭 裴培 黄瑜 王斌

摘要： 为分析冻融环境下钢筋混凝土（RC）梁在地震荷载作用下的响应，采用人工环境模拟方法对4件RC梁试件进行了快速冻融试验，进而对其进行拟静力加载试验。结果表明，随着冻融次数的增加，梁试件滞回曲线的捏缩现象越发明显，构件延性和耗能能力下降。同时，通过理论推导建立了可考虑冻融损伤的粘结滑移模型，采用有限元分析软件OpenSEES中的零长度截面单元，并基于可考虑冻融损伤分布的纤维截面模型，对RC梁试件的地震破坏过程进行了数值模拟。分析与试验结果对比表明，采用数值建模与分析方法得到的滞回曲线与试验数据基本相符，骨架曲线诸特征值误差较小，且较好地反映了冻融损伤引起RC梁滞回曲线的捏缩效应，从而验证了所提出的模拟方法的准确性。

关键词： RC梁; 抗震性能; 冻融循环; 粘结?滑移; 滞回曲线

中图分类号： TU352.11; TU375.4 文献标志码： A 文章编号： 1004-4523（2021）05-0889-10

DOI：10.16385/j.cnki.issn.1004-4523.2021.05.002

引 言

中国地域辽阔，其中东北、华北和西北大部分地区属于严寒或寒冷地区，这些地区的钢筋混凝土（RC）易遭受冻融循环作用，导致钢筋混凝土材料性能及粘结性能发生退化，从而造成RC结构的受力性能和抗震性能的劣化[1?2]。严寒地区的冻融循环作用已成为影响RC结构耐久性问题的一个重要因素，引起了国内外学者的广泛关注。施士升[3]、Hanjari[4]等通过试验分析，揭示了混凝土抗压强度、抗拉强度、弹性模量等性能指标随冻融循环次数变化的退化规律。文献[5]进一步指出混凝土材料耐久性能的逐步退化将会导致RC构件与结构力学性能和抗震性能不断劣化。在这一背景下，Xu等[6]、郑捷等[7]、郑山锁等[8]通过拟静力加载试验，分别探讨了RC框架柱、框架节点及剪力墙试件在不同冻融次数下的抗震性能退化规律;张艺欣等[9]则考虑混凝土冻融损伤在构件内部分布的不均匀性，提出了冻融RC柱的数值模拟方法，并据此对不同冻融循环次数下RC柱的抗震性能展开了研究。然而，该数值模拟方法中并未考虑冻融损伤条件下钢筋与混凝土间的粘结性能劣化。Hadadd等[10]和Fagerlund等[11]通过试验研究发现，冻融循环作用会导致钢筋与混凝土间的粘结强度退化，并引起自由端的滑移变形不断增大。Ma等[12]，Saatcioglu等[13]和Moehle等[14]通过试验研究发现，由钢筋滑移产生的固端转角所引起的变形在RC构件整体变形中可达到50%。因此，为较好地反映冻融RC结构的力学性能和变形能力，Hanjari等[15]基于欧洲规范[16]中粘结滑移模型，提出了考虑冻融影响的粘结滑移模型;然而，该模型仅考虑冻融对粘结强度的影响，忽略了滑移量的变化，且没有考虑冻融破坏范围的延伸和分布情况，即缺乏对冻融不均匀性的考虑[17]。

鉴于此，本文首先对4件不同冻融次数下的RC梁试件进行了拟静力试验，系统地研究了不同冻融次数对其抗震性能的影响规律;进而通过理论推导，并结合已有研究成果，建立了考虑冻融损伤影响的钢筋与混凝土材料界面粘结滑移本构模型。据此，采用纤维模型并考虑冻融损伤在构件内部分布的不均匀性以及粘结滑移影响，对上述4件RC梁进行了数值建模分析，通过与试验结果对比分析，验证了所建立的粘结滑移本构模型和数值建模方法的准确性与可行性。该成果将为冻融大气环境下在役RC结构的抗震性能研究奠定基础。

1 试验概况

1.1 试件设计与制作

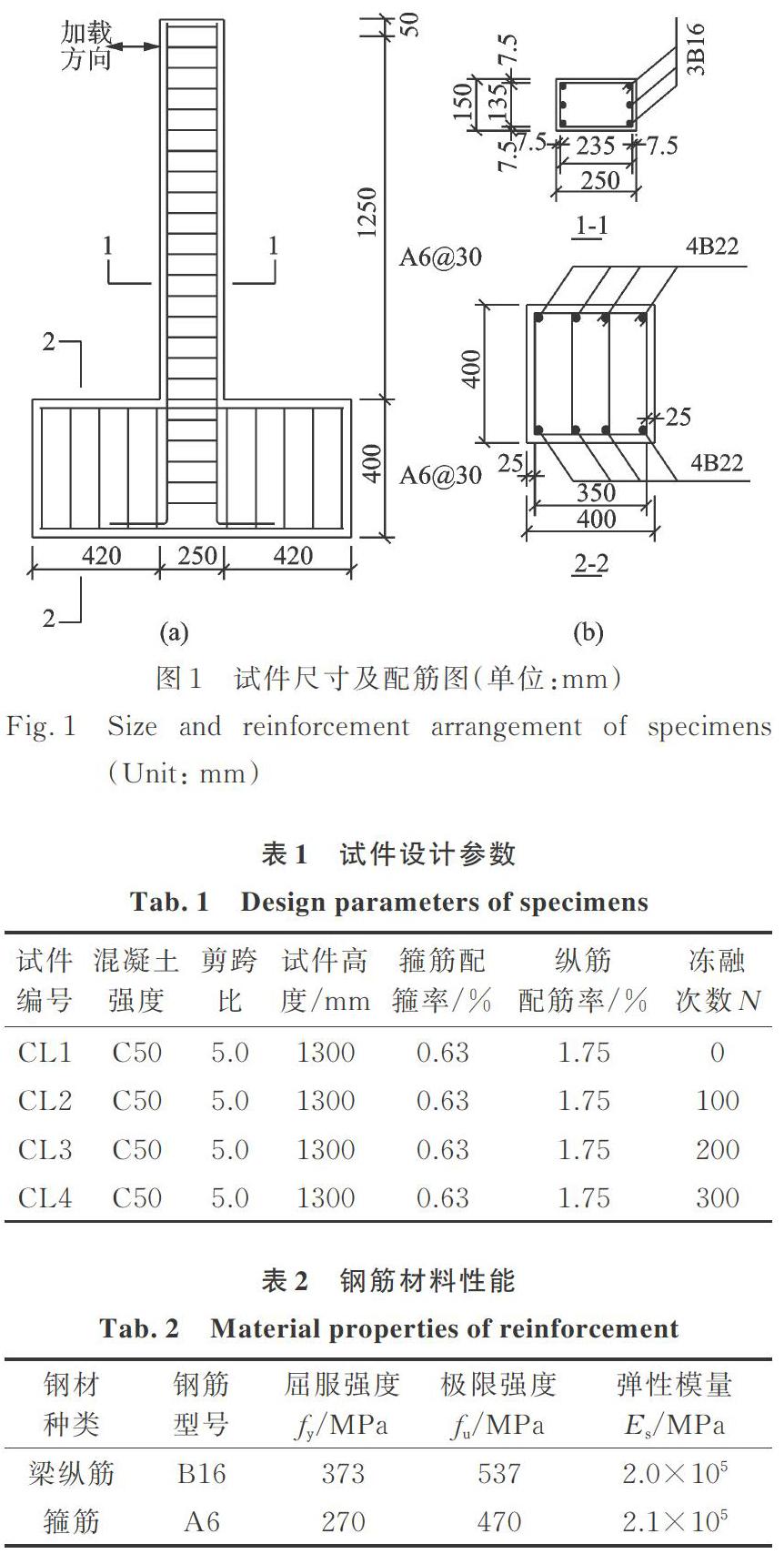
地震作用下，RC框架梁端部易发生损伤破坏，且其跨中存在反弯点，故本文取梁端至反弯点间梁端为研究对象，按照1∶2的缩尺比例设计了4件相同设计参数、不同冻融循环次数的RC梁试件（剪跨比），试件设计参数如表1所示，试件尺寸及配筋图如图1所示。钢筋材料力学性能实测数据及混凝土配合比如表2与表3所示;在梁试件制作的同期，浇筑边长150 mm的标准立方体试块，用于测量冻融前后混凝土立方体抗压强度。

1.2 冻融循环方案

中国规范[18]中的“气冻水融”条件的慢冻法与“水冻水融”条件的快冻法仅适用于小尺寸混凝土试件，且其试验条件对于RC梁来说很少在自然环境中真实存在。本试验参考规范[18]中的慢冻法实施过程，采用人工气候环境模拟实验技术，通过控制实验室中空气的温度来实现冻融循环过程中的温度变化，模拟“气冻气融”的自然冻融环境。为获得良好的冻融效果，试件冻融前需充分浸泡且冻融过程中需间断喷淋，使试件处于饱和水状态。每个冻融循环总时长5.5 h，用于降温及冷冻的时间为4 h，用于升温、融化及喷淋的时间为1.5 h。本次试验冻融循环方案如图2所示。

1.3 冻融后混凝土材料性能

冻融试验后，测量4组（每组3个）RC梁伴随立方体试块抗压强度，结果如表4所示。可以发现，随着冻融次数增加，混凝土抗压强度不断降低，在经过300次冻融循环后，混凝土强度下降幅度超过30%。试验结果表明了冻融损伤对混凝土性能的不利影响。

1.4 拟静力加载方案与制度

为准确模拟RC框架梁在地震作用下的实际受力状况，采用“悬臂梁”式及位移控制加载方式对各梁试件进行拟静力加载，具体方案如下：试件屈服前，位移增量为理论计算屈服位移Δy[19]的0.2倍，每级控制位移循环1次;试件屈服后，位移增量为Δy，每级控制位移循环3次;当承载力降至峰值荷载Pc的85%后或破坏明显时停止试验加载。加载系统及加载制度如图3和图4所示。

1.5 拟静力试验结果

试验加载结束时，梁试件在往复荷载作用下均发生弯曲破坏，各试件破坏过程相似。以未冻融试件CL1为例：随着试验加载的进行，当梁顶部水平位移达到1.4 mm时，距梁底部约200 mm高处开始出现初始水平裂缝，标志梁进入了开裂阶段，此后加载继续进行，裂缝不断延伸并加宽，并伴有新的水平裂缝出现;当位移达到2.7 mm时，梁的角端部位出现开裂现象，且距梁底约250，300，350 mm处陆续出现了水平裂缝，继续加载，梁底纵向受拉钢筋逐步屈服，距梁底约350 mm高处的水平裂缝斜向发展为斜裂缝;随着加载的进行，部分斜裂缝延伸至梁底角部，角部水平裂缝逐步贯穿，裂縫宽度明显增加，角部混凝土受到严重挤压;水平位移超过32 mm后，梁底部形成两条明显的主推与主拉水平裂缝;水平位移超过65 mm后，梁底角部大部分混凝土破碎脱落，钢筋外露，试件承载力迅速下降，试件宣告破坏。试件加载过程中裂缝分布图如图5所示。

随冻融次数的增多，梁底部水平裂缝出现提前，试件表面裂缝数量增加，梁顶水平荷载到达峰值后下降速率加快，塑性铰区斜裂缝发展相对迅速，破坏时试件角部混凝土提前被压碎，呈现颗粒状，而不是块状，破坏更为严重。由于冻融后混凝土强度降低，纵筋提前屈服，梁受压区混凝土酥碎更为严重，钢筋与混凝土的粘结性能弱化导致使钢筋中应力通过粘结应力传递给混凝土时所需传力长度增长，裂缝间距增大，试件延性随着冻融次数的增多逐步降低。各试件的破坏状态图如图6所示。

分析各梁试件的滞回曲线（如图7所示）可知：滞回环的捏缩现象随冻融次数增多越发明显，所包围的面积逐渐减小，表明冻融循环加剧了钢筋与混凝土间的粘结性能退化，降低了梁的耗能能力。根據滞回曲线，得到如图8所示不同冻融次数下梁骨架曲线，表5特征点参数由正负向平均骨架曲线标定，其中屈服点由“能量法”[20]而定，极限点取为荷载降至0.85Pc的对应点，累积耗能按计算确定（其中，Ei为第i次循环加载正反循环一周时构件耗散能量，N为循环加载次数）。

从图8和表5可以看出，梁试件的屈服位移Δy和峰值位移Δc均随冻融循环次数增多而逐渐增大，极限位移Δu逐渐减小，从而延性系数（）不断降低;屈服荷载Py、峰值荷载Pc和极限荷载Pu均随冻融循环次数的增多而呈降低趋势，但相比于表4冻融后混凝土抗压强度降低程度而言该降低趋势并不显著，其原因为：冻融损伤是从混凝土表层向其内部发展的，梁试件尺寸相对较大，仅表层出现冻融损伤，而材性试验中混凝土试块尺寸较小，故其冻融损伤相对严重。

2 考虑冻融损伤的粘结滑移本构模型

既有研究结果显示[10]，冻融作用会致使钢筋和混凝土间粘结强度下降，滑移变形增大，因此，为准确反映冻融损伤RC梁的力学性能与抗震性能，有必要在建立粘结滑移本构模型时考虑冻融损伤影响。冻融后钢筋混凝土间粘结性能劣化主要是由混凝土力学性能退化所引起，因此，本文首先介绍未冻融损伤钢筋与混凝土间的粘结滑移本构模型，继而考虑冻融循环作用对混凝土力学性能的影响，对该模型进行修正，建立考虑冻融损伤的粘结滑移本构模型。

2.1 粘结滑移本构模型

钢筋与混凝土间的粘结应力分布不仅受混凝土强度、钢筋直径、保护层厚度、横向约束等多种因素影响，还涉及位置函数等复杂变量[21]。Yu等[22]指出，在结构分析中如果直接应用粘结应力与滑移量s表示的粘结滑移关系将会增加数值建模的复杂性;因此，基于钢筋应力与粘结应力良好的相关性，本文在数值模拟中采用钢筋应力与滑移量s表示的粘结滑移本构关系，以避免分析过程中复杂的微分迭代计算及位置函数的引入，简化计算过程。Zhao等[23]提出将零长度纤维单元与普通纤维单元串联的思路，并在零长度截面中采用钢筋应力?滑移本构关系替代传统钢筋应力?应变关系，以模拟悬臂构件的弯曲变形和滑移变形，并进行了广泛应用[24?27]。本文基于此研究思路，首先通过钢筋应力?粘结应力?钢筋应变?滑移量间相关关系推导得出钢筋应力?滑移本构关系，进而将该本构关系赋予零长度单元中的钢筋，以模拟梁端滑移量，最终得到考虑粘结滑移效应的梁端转角或梁顶侧向位移。

Altoontash[28]在模型分析中采用表示的粘结滑移关系，并提出如下假设：1）根据能量耗散等效原理，分别将钢筋应力小于和大于fy长度上的粘结应力假定为均匀分布的平均粘结应力和（如图9所示）;2）滑移是钢筋与混凝土间相对变形的结果;3）钢筋应力为0时相应的滑移量也为0。此外，Otani等[29]也曾将钢筋与混凝土间的粘结应力分布假定为沿钢筋应力发展长度上的均匀分布，Sezen等[30]则在Otani的基础之上提出了阶梯状均匀分布的粘结应力分布模式，并将其应用于分析模型中，取得了良好的模拟效果。

基于上述分析，本文依据钢筋是否达到屈服强度，将钢筋与混凝土间的粘结应力分布划分为如图10所示两种情况，并据此建立由关系表示的粘结滑移本构模型。其中钢筋应变根据双线型本构关系定义如下

式中 为钢筋应力，为钢筋屈服强度;为钢筋弹性模量;为钢筋硬化模量，取为的2.5%。

根据图10，建立钢筋与混凝土间的粘结滑移关系如下：

（1）钢筋屈服前，其与混凝土间的粘结应力沿钢筋应力发展长度ls呈均匀的分布（如图10（a）所示），则由力学平衡关系可得

式中 为钢筋应力，;d和As分别为钢筋直径和横截面面积;为钢筋应力发展长度上均匀分布的平均粘结应力，参考Lowes等[31]的研究结果，其值取为1.4，为混凝土抗压强度。

钢筋锚固滑移量s为钢筋应力发展长度上钢筋的累积变形，其值按下式计算：

式中 和分别为锚固钢筋应力小于和大于fy区段的长度;为沿分布的平均粘结应力，根据文献[31]取为0.4。

当钢筋应力达到极限强度时，钢筋应变渗透引起的滑移达到极限滑移值su。则由式（5）可得

基于以上分析，建立未冻融损伤下钢筋与混凝土间以钢筋应力与滑移量s表示的粘结滑移本构关系，如下式所示

具体模型见图11中0次冻融曲线。

2.2 修正的粘结滑移本构模型

Fagerlund等[11]通过试验研究发现，冻融损伤将导致钢筋与混凝土间的粘结强度不断降低，且下降幅度在30%?70%之间;Hanjari等[32]的研究结果表明，冻融损伤混凝土抗压强度降低25%?50%时，其与钢筋间的粘结强度退化约15%?50%;Petersen等[17]则发现，当冻融损伤程度较轻时，试件破坏仅限于混凝土保护层的开裂剥落，且在最大粘结强度下可以观察到微小的滑移增长量;当冻融损伤深入试件内部，即冻融损伤程度较重时，钢筋与混凝土粘结强度骤降，滑移量显著增大，且随冻融损伤程度的加剧，钢筋混凝土间粘结性能退化愈加严重。上述研究结果均表明，冻融损伤对钢筋与混凝土间粘结性能的影响不容忽视。因此在建立钢筋与混凝土粘结滑移本构模型时有必要考虑冻融损伤的影响。

冻融损伤后，钢筋混凝土粘结性能劣化的主要原因在于混凝土力学性能的退化，因此，本文通过考虑冻融循环作用对混凝土力学性能的影响，对2.1中给出的粘结滑移本构模型进行修正，以建立考虑冻融损伤影响的粘结滑移本构模型。具体方法如下：

（1）冻融混凝土抗压强度

张艺欣等[9]以相对动弹性模量（RDME）为参数，建立了冻融混凝土抗压强度计算模型，其表征如下

式中 R为冻融损伤后不同深度处混凝土的RDME;N为冻融循环次数;为冻融混凝土动弹性模量开始发生退化时的临界冻融循环次数;xi为试件内部混凝土到试件受冻边缘的最小距离。

然而，需要指出的是：上述公式中的N为Petersen冻融试验方法中的冻融循环次数[17]，本试验中各试件的冻融方法与Petersen的不同，因而同样冻融次数下混凝土的冻损程度并不一致，从而公式（10）无法直接应用于本研究中。文献[9]以RDME退化程度相同作为等效原则，建立了其试验条件下的冻融循环次数NE与Petersen试验条件下冻融循环次数NP的对应关系（如表6所示），本试验中各试件的冻融试验条件与文献[9]的相同。因此，可采用表6中的对应关系，将本试验的冻融循环次数变换为Petersen试验的冻融循环次数。

（2）考虑冻融影响的钢筋混凝土粘结滑移本构模型

基于钢筋与混凝土间粘结强度与混凝土抗压强度间的关系，将修正后的混凝土抗压强度公式（10）代入式（9），即可得考虑冻融损伤影响的钢筋混凝土粘结滑移本构关系

式中 为冻融混凝土抗压强度，根据式（10）计算确定。据此，得到不同冻融循环次数下以钢筋应力与滑移量s表示的粘结滑移本构关系，如图11所示。可以看出，随冻融循环次数增多：钢筋屈服前，钢筋与混凝土间的滑移变形缓慢增长;而当钢筋屈服后，在较大的应变渗透作用影响下，滑移变形显著增大。

3 有限元建模及模型验证

为验证所建立的考虑冻融影响的钢筋混凝土粘结滑移本构模型的准确性，基于OpenSees有限元分析平台，采用纤维模型并考虑冻融损伤的不均匀性及锚固粘结滑移影响，建立冻融损伤RC梁试件的数值模型。

3.1 数值建模

文献[9]将其提出的冻融混凝土“不均匀损伤”模型及RC柱拟静力试验结果与段安[33]提出的冻融混凝土“全截面损伤”模型进行对比，分析不同冻融次数、轴压比及混凝土强度因素下试验与模拟结果的滞回曲线，结果表明不均匀损伤模型更接近于试验结果，可以良好地模拟冻融损伤后的RC柱构件地震反应。然而，该模型中并未考虑冻融损伤条件下钢筋与混凝土间的粘结性能劣化。

本文参考文献[9]，采用纤维模型模拟RC梁的弯曲变形，并考虑不同深度处混凝土冻融损伤的不均匀性，将构件不同深度处混凝土纤维分别赋予不同的冻融损伤混凝土本构关系，具体数值建模方法及冻融损伤混凝土本构模型参数标定方法参见文献[9]。同时，为考虑冻融后混凝土与钢筋间粘结性能劣化对RC梁力学与抗震性能的影响，引入零长度截面单元（zeroLengthSection）模拟梁锚固端纵筋的粘结滑移效应，通过串联非线性梁柱单元与零长度截面单元，形成RC梁整体数值分析模型，如图12所示。根据构件配筋及等效塑性铰高度，模型沿梁高划分6个单元，节点1与节点6之间为非线性纤维梁柱单元，节点1与节点7之间为零长度截面单元。该零长度单元截面中的混凝土本构采用Concrete01模型，并参考文献[7]，考虑不同深度处混凝土冻融损伤的不均匀性;钢筋材料本构则采用Pinching4模型，以反映往复加载过程中粘结滑移滞回曲线的捏缩效应以及加、卸载刚度退化和强度衰减现象，Pinching4模型骨架曲线参数根据本文第2节中公式（13）计算确定，滞回规则控制参数则参考文献[25]确定。

3.2 模型验证

基于上述建模方法，分别对不同冻融循环次数下的RC梁试件进行数值建模与分析，并将分析结果与试验的结果进行对比，其中滞回曲线对比如图13所示。

由图13可以看出，4件RC梁试件数值分析得到的滞回曲线与试验滞回曲线均呈现出明显的捏缩现象，模拟所得各阶段刚度及滞回性能与试验测试结果基本一致，整体吻合较好。同时，对比模拟与试验所得屈服点和峰值点的特征值（如图14所示），可以看出其误差基本不超过15%，表明采用本文建立的数值模型所得各试件骨架曲线与试验结果符合较好，能够对冻融RC梁各阶段受力性能进行较准确的模拟。分析误差产生的原因：一方面是由于本文在数值模拟中采用的冻融循环次数是基于文献[9]试验回归分析得到的等效冻融循环次数，这与实际结果之间存在一定的差异;其次，由于所建立模型中未考虑剪切变形的影响，并忽略了冻融引起的试件剪切剛度退化，从而导致模拟滞回曲线的卸载刚度大于试验值，并高估了结构实际变形能力，致使模拟得到的结构耗能和承载力均略大于试验结果。

4 结 论

本文采用试验研究、理论推导及数值建模与分析相结合的方法，研究了冻融RC梁抗震性能劣化规律及其考虑粘结滑移影响的数值建模分析方法，主要成果与结论如下：

（1）随着冻融次数增多，RC梁滞回曲线的捏缩现象越发明显，延性和耗能能力均不断降低，表明冻融循环将导致钢筋与混凝土间粘结性能劣化。

（2）建立了考虑冻融影响的钢筋混凝土粘结滑移本构模型，分析与试验的结果对比表明，所建模型能够较准确地反映冻融损伤后钢筋与混凝土间粘结性能的劣化规律。

（3）建立了可考虑冻融损伤不均匀分布、粘结滑移效应和等效冻融循环次数的冻融RC梁纤维截面模型及其数值建模分析方法，对比分析表明，其数值模拟方法可较好地反映冻融RC梁的力学与抗震性能退化规律。

参考文献：

[1] MEHTA P K. Concrete durability： Fifty years progress[C]. Proceedings of 2nd International Conference on Concrete Durability. Farmington Hills， MI： American Concrete Institute， 1991： 1-33.

[2] 张士萍， 邓敏， 唐明述. 混凝土冻融循环破坏研究进展[J]. 材料科学与工程学报， 2008，26（6）：990-994.

ZHANG Shiping， DENG Min， TANG Mingshu. Advance in research on damagement of concrete due to freeze-thaw cycles[J]. Journal of Materials Science and Engineering， 2008，26（6）：990-994.

[3] 施士升. 冻融循环对混凝土力学性能的影响[J]. 土木工程学报， 1997，30（4）：35-42.

Shi Shisheng. Effect of freezing-thawing cycles on mechanical properties of concrete[J]. China Civil Engineering Journal， 1997，30（4）：35-42.

[4] Hanjari K Z. Structural behaviour of deteriorated concrete Structures[D]. Gothenburg： Chalmers University of Technology， 2010.

[5] D'Ambrisi A， De Stefano M， Tanganelli M， et al. Influence of the variability of concrete mechanical properties on the seismic response of existing RC framed structures[M]∥Seismic Behaviour and Design of Irregular and Complex Civil Structures. Geotechnical， Geological and Earthquake Engineering， 2013， volume 24. Springer， Dordrecht.

[6] XU Shanhua， LI Anbang， JI Zengyang， et al. Seismic performance of reinforced concrete columns after freeze?thaw cycles[J]. Construction & Building Materials， 2016， 102：861-871.

[7] 郑 捷， 董立国， 秦 卿，等. 冻融循环下钢筋混凝土框架梁柱中节点抗震性能试验研究[J]. 建筑结构学报， 2016， 37（10）：73-81.

Zheng Jie， Dong Liguo， Qin Qing， et al. Experimental study on seismic behaviors of RC beam-column joints after freeze-thaw cycles[J]. Journal of Building Structures， 2016， 37（10）：73-81.

[8] 郑山锁， 甘传磊， 秦 卿， 等. 冻融循环后一字形短肢剪力墙抗震性能试验研究[J]. 工程力学， 2016， 33（12）：94-103.

Zheng Shansuo， Gan Chuanlei， Qin Qing， et al. Experimental study on the seismic behavior of short-pier shear walls subjected to freeze-thaw cycles [J]. Engineering Mechanics， 2016， 33（12）： 94-103.

[9] 张艺欣， 郑山锁， 裴 培， 等. 钢筋混凝土柱冻融损伤模型[J]. 工程力学， 2019，36（2）：78-86.

Zhang Yixin， Zheng Shansuo， Pei Pei， et al. Research on the modelling method of reinforced concrete column subjected to freeze-thaw damage[J]. Engineering Mechanics， 2019，36（2）：78-86.

[10] Haddad R H， Numayr K S. Effect of alkali-silica reaction and freezing and thawing action on concrete?steel bond[J]. Construction & Building Materials， 2007， 21（2）： 428-435.

[11] Fagerlund G， Janz M， Johannesson B. Effect of frost damage on the bond between reinforcement and concrete[R]. Division of Building Materials， Lund Institute of Technology， Sweden， 1994.

[12] Ma S Y M， Bertero V V， Popov E P. Experimental and analytical studies on hysteretic behaviour of recnforced concrete rectangular and T-beam[R]. University of California， Berkeley， 1976， Rep. No. EERC 76-2.

[13] Saatcioglu M， Ozcebe G. Response of reinforced concrete columns to simulated seismic loading[J]. ACI Structural Journal， 1989， 86（1）： 3-12.

[14] Moehle J P， Lehman D E. Seismic performance of confined concrete bridge columns[C]. International Symposium on Confined Concrete. Changsha， China， 2006， 238： 23-42.

[15] Hanjari Kamyab Z， Kettil Per， Lundgren Karin. Modelling the structural behavior of frost-damaged reinforced concrete structures[J]. Structure & Infrastructure Engineering， 2013， 9（5）： 416-431.

[16] Euro-International Committee for Concrete. CEB-FIP Model Code 1990[S]. London： Thomas Telford， 1993.

[17] Petersen L， Lohaus L， Anna M P. Influence of freezing-and-thawing damage on behavior of reinforced concrete elements[J]. ACI Materials Journal， 2007， 104（4）： 369-378.

[18] GB/T 50082-2009，普通混凝土长期性能和耐久性能试验方法标准[S]. 北京： 中国建筑工业出版社， 2009.

GB/T 50082-2009， Standard for test methods of long-term performance and durability of ordinary concrete [S]. Beijing： China Building Industry Press， 2009.

[19] Watson S， Park R. Simulated seismic load tests on reinforced concrete columns[J]. Journal of Structural Engineering， 1996， 120（6）： 1825-1849.

[20] Mahin S A ， Bertero V V. Problems in establishing and predicting ductility in aseismic design[C]. Proceedings of the International Symposium on Earthquake Structural Engineering， St. Louis， USA， 1976： 613-628.

[21] Somayaji S， Shah S P. Bond stress versus slip relationship and cracking response of tension members[J]. Journal of the American Concrete Institute， 1981， 78（3）： 217-225.

[22] Yu J， Tan K H. Bar stress-slip relationship in reinforced concrete joints with large inelastic bar strains[C]. International Conference of Design and Analysis of Protective Structures， 2012.

[23] Zhao J， Sritharan S. Modeling of strain penetration effects in fiber-based analysis of reinforced concrete structures[J]. ACI Structural Journal， 2007， 104（2）： 133-141.

[24] 楊 红， 徐海英， 王志军. 考虑柱底纵筋滑移的纤维模型及框架地震反应分析[J]. 建筑结构学报， 2009， 30（4）： 130-137.

YANG Hong， XU Haiying， WANG Zhijun. Seismic responses analysis of RC frame based on fiber model considering bar slippage at column bottom section[J]. Journal of Building Structures，2009，34（4）：130-137.

[25] Melo J， Fernandes C， Varum H， et al. Numerical modelling of the cyclic behavior of RC elements built with plain reinforcing bars?[J]. Engineering Structures， 2011， 33（2）： 273-286.

[26] Jeon J， Lowes L N， Desroches R， et al. Fragility curves for non-ductile reinforced concrete frames that exhibit different component response mechanisms[J]. Engineering Structures， 2015， 85： 127-143.

[27] 孙治国， 陈 灿， 司炳君， 等. 考虑非线性剪切效应的RC桥墩抗震分析模型[J]. 工程力学， 2015， 32（5）： 28-36.

SUN Zhi-guo， CHEN Can， SI Bing-jun， et al. Seismic analysis model considering nonlinear shear effect for RC bridge piers[J]. Engineering Mechanics， 2015， 32（5）： 28-36.

[28] Altoontash A. Simulation and damage models for performance assessment of reinforced concrete beam?column joints[D]. Stanford： Stanford University， 2004.

[29] Otani S， Sozen M A. Behavior of multistory reinforced concrete frames during earthquakes[D]. Urbana， IL：University of Illinois， 1972.

[30] Sezen H， Moehle J P. Bond-slip behavior of reinforced concrete members [C]. Fib Symposium （CEB-FIP）， Concrete Structures in Seismic Regions. Athens， Greece， 2003.

[31] Lowes L N， Altoontash A. Modeling reinforced-concrete beam-column joints subjected to cyclic loading [J]. Journal of Structural Engineering， 2003， 129（12）： 1686-1697.

[32] Hanjari K Z， Utgenannt P， Lundgren K. Frost-damaged concrete： Part 2. Bond properties [C]. International Conference on Construction Materials： Performance， Innovations and Structural Implications. 2009： 761-766.

[33] 段 安. 受凍融混凝土本构关系研究和冻融过程数值模拟[D]. 北京： 清华大学， 2009.

Duan An. Research on constitutive relationship of freeze-thawed concrete and mathematical modeling of freeze-thaw process [D]. Beijing： Tsinghua University， 2009.

作者简介： 郑山锁（1960?），男，教授。电话：13991835628; E?mail： zhengshansuo@263.net

通讯作者： 杨 路（1999?），女，硕士研究生。电话：18829045739; E?mail： yl2946584790@163.com