基于有限元极限平衡法的岩土结构稳定分析
邵龙潭,王浩然,姜泽涵
(1.大连理工大学工业装备结构分析国家重点实验室,辽宁 大连 116024;2.中山大学土木工程学院,广东 珠海 519082;3.大连理工大学白俄罗斯国立大学联合学院,辽宁 大连 116024)
在土力学中,有三大经典问题,即边坡稳定、土压力和地基承载力。有学者指出,这三个问题都可表征为边坡的稳定分析问题。土压力问题是一个具有垂直表面的边坡稳定问题,地基承载力问题是一个具有水平表面的边坡稳定问题[1],而边坡稳定最常见的地质灾害是滑坡,滑坡的发生是从一点的破坏开始的[2]。我国是一个地质灾害十分严重的国家,据统计,我国每年由地质灾害所造成的经济损失达200亿~500亿人民币[3]。
边坡稳定性分析是坡体结构设计、失稳防护的基础。目前,边坡稳定性分析方法主要有极限平衡法、极限分析法和以有限元为主的数值分析方法等。在分析土压力问题时,郑颖人等[4]采用极限平衡法的思想假定挡土墙后土体处于极限平衡状态计算土体主动与被动土压力。也有学者将边坡划分为若干竖条,通过分析作用在土条上力和力矩的平衡关系对边坡的稳定性能进行评价。极限分析方法是应用刚塑性材料处于极限状态的上下限定理求解极限载荷的一种解析方法。
采用有限元法分析边坡稳定性又可分为有限元强度折减法与有限元极限平衡法。有限元强度折减法是将土体强度参数进行折减,将土体破坏时的折减系数视为安全系数,该方法存在的问题是破坏判别标准不统一、需要反复迭代计算、不同的材料取相同的折减系数不合理以及强度折减可能会影响材料的应力应变关系参数从而导致有可能违背材料自身性质等[5-7]。有限元极限平衡法依据极限平衡理论定义安全系数,根据有限元计算得到的应力分布确定临界滑动面及其相应的安全系数,进而进行岩土结构稳定性分析。大量实践结果表明,有限元极限平衡法可用于各种岩土结构的稳定分析[8-11]。
1 滑动稳定安全系数定义
应用莫尔-库伦强度准则,邵龙潭等[11]将土体内一点的极限平衡条件推广到曲面,得到任意曲面上任意形状土体的极限平衡条件。对于并未处于极限平衡状态的实际岩土结构,采用折减抗剪强度或者增加荷载的方法令其达到沿曲面的极限平衡状态,由此可以得到定义安全系数,并且发现滑动面上抗剪力与剪切力代数和之比的安全系数定义的物理意义,既是曲面上任意形状的土体达到极限平衡状态时抗剪强度强度折减系数的中值,也是使曲面上土体沿着曲面达到极限平衡的超载系数的中值[12]。
1.1 土体内一点的极限平衡条件
土体抵抗剪切破坏的能力称为土的抗剪强度。在常见压力范围内,土的抗剪强度主要由颗粒之间的联结性质决定。莫尔-库伦通过试验发现土在滑动面上的抗剪强度与法向应力成正比,见式(1)。
τf=σntanφ+c
(1)
式中:τf为土的抗剪强度;c为黏聚力;φ为内摩擦角;σn为滑动面上的正应力。
当土工结构中任意一点的土体在某一方向上的剪应力τ等于土的抗剪强度τf时,就称该点的土处于极限平衡状态,一点土体的极限平衡条件见式(2)。
τ=τf
(2)
当一点土体处于极限平衡状态时,该点对应的土体微元体也在对应方向上达到极限平衡状态[12]。
1.2 滑动面上土体的极限平衡条件
将一点的极限平衡状态扩展到土体沿某一曲线(面)的极限平衡状态。假设l为土体区域内的任意形状连续曲线,土体沿l达到极限平衡状态是指在曲线任意微元长度上,沿曲线切线方向土体的滑动力(剪应力)与阻滑力(抗剪力)相等。
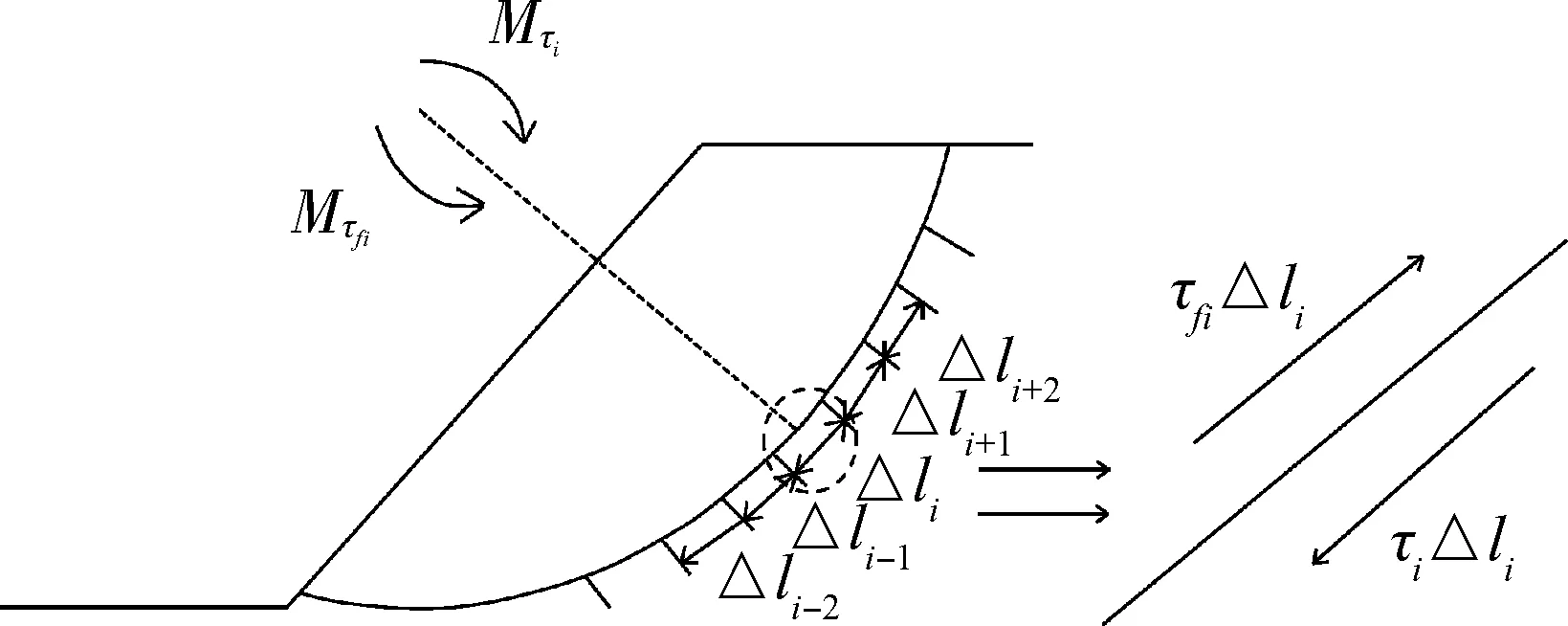
图1 滑动面上一微元体沿切线方向的力和力矩的平衡Fig.1 The equilibrium condition in the sliding surfacealong the tangent direction
如图1所示,若土体沿滑动面任意一点都处于极限平衡状态,见式(3)。
τi-τfi=0
(3)
由式(3)可知,滑动面上每一点对应的微元长度上土体的滑动力与阻滑力相平衡,得式(4)。
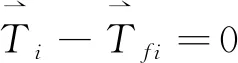
(4)
此时,整个滑动面上土体滑动力的合力与阻滑力的合力也相平衡(式(5)),对于滑动面外任意一点,滑动力矩与阻滑力矩的合力矩也平衡,见式(6)。
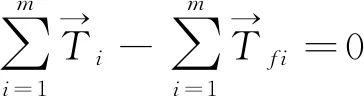
(5)

(6)
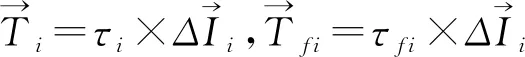
任意一个曲面上,如果任意一点的土体都处于极限平衡状态,则以该曲面为底的任意形状的土体都处于极限平衡状态,称为土体沿着该曲面达到极限平衡状态。邵龙潭等[11]证明,土体沿着曲面达到极限平衡的充分必要条件见式(7),证明过程见图2。

(7)

图2 曲面上土体极限平衡的充分必要条件证明Fig.2 Proof of the necessary and sufficient conditions for the soil’s limit equilibrium on the curved surface
1.3 沿曲面滑动稳定安全系数的定义
对于一个稳定的土体结构,人为地减小土体的抗剪强度使其达到极限平衡状态。假设R(l)为沿曲面(线)l使土体各点均达到极限平衡状态的强度折减系数函数,l为土体结构内的任意曲面(线),那么土体沿着曲面(线)l达到极限平衡的充要条件见式(8)。

(8)
设定l为闭区间,在剪应力方向不变的条件下可以应用积分中值定理,得式(9)。
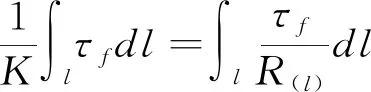
(9)
土体沿该曲面的安全系数可以表示为式(10)。

(10)
同样地,假设P(l)为沿曲面(线)l使土体各点均达到极限平衡状态的超载系数函数,那么土体沿着曲面(线)l达到极限平衡的充要条件为式(11)。

(11)
此时中值定理可以表示为式(12)。

(12)
由此可知,安全系数K不仅是土体在曲面上达到极限平衡的抗剪强度强度折减系数的中值,也是使曲面上土体沿着曲面达到极限平衡的超载系数的中值。曲面(线)l既可以是贯穿岩土结构的整体曲面,也可以是在岩土结构内部的局部曲面,说明用此安全系数作为评价标准,既可以分析土体结构整体的滑动稳定性,也可以分析土体的局部破坏区域[12-13]。
2 安全系数和最危险滑动面的求解
根据上述理论,在实际计算中,土体沿某一滑动面的安全系数可以表示为式(13)。

(13)
将滑动面离散成m个微小单元i,安全系数可以表示为式(14)。

(14)
采用一维线性单元平面坐标转换与二阶高斯积分,安全系数可以进一步表示为式(15)。

(15)
式中,|J|为Jacobian矩阵行列式,其表达式为式(16)。
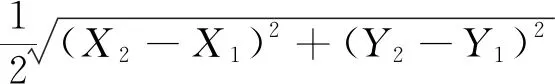
(16)

对于任意土体微元,在确定了高斯积分点坐标值以后,首先需要判断该高斯点在哪一个有限元单元网格内,然后再根据距离倒数加权平均法得到该点应力,并结合土体微元的方向得到高斯积分点沿土体微元方向的剪应力与抗剪强度,根据式(15)可计算出土体沿该滑动面的安全系数。
3 应用算例
3.1 均质土坡稳定性分析
采用费康等[14]的算例,某均质边坡高H=10 m,边坡倾角为45°(图3)。土体容重为20 kN/m3,内摩擦角φ=20°,黏聚力c=12.38 kPa,弹性模量E=100 MPa,泊松比v=0.35。有限元计算利用商业软件Abaqus6.14,采用理想弹塑性本构模型进行计算。模型底部为固定约束,左右边界为水平约束。
图4为有限元极限平衡法分析结果,图4中边坡区域内线段表示安全系数为1.00~1.01,1.01~1.02,1.02~1.03,1.03~1.04,1.04~1.05的局部滑动面线段。从图4中可以看出,安全系数临近1.0的线段主要集中在x=7到x=15之间,说明该范围内的土体安全系数较低。
表1为瑞典圆弧法、BISHOP法、有限元强度折减法、有限元极限平衡法计算得到的安全系数。 图5为有限元极限平衡法计算得到的临界滑动面上土体的剪应力和抗剪强度分布情况。从图5中可以看出, 坡体剪应力分布符合一般规律。 在坡体表面(x=16.4处),剪应力接近于0,随滑动面土体埋深的增加,土体剪应力与抗剪强度增加。在x=11.7处,滑动面埋深达到最大,同时剪应力与抗剪强度达到峰值,随后滑动面埋深变化不大,剪应力与抗剪强度变化不大。在坡脚处(x=2处)滑动面埋深虽为0,但其沿临界滑动面的剪应力并不为0,说明坡脚处承受一定的水平力作用,建议在坡脚处增加抗滑措施。在x=7到x=15之间的滑动面安全系数较低,这也与局部稳定性分析得到的结论吻合。

图3 均质边坡示意图Fig.3 Schematic diagram of homogeneous slope

图4 计算得到的局部破坏区与临界滑动面Fig.4 Calculated local failure area and critical sliding surface
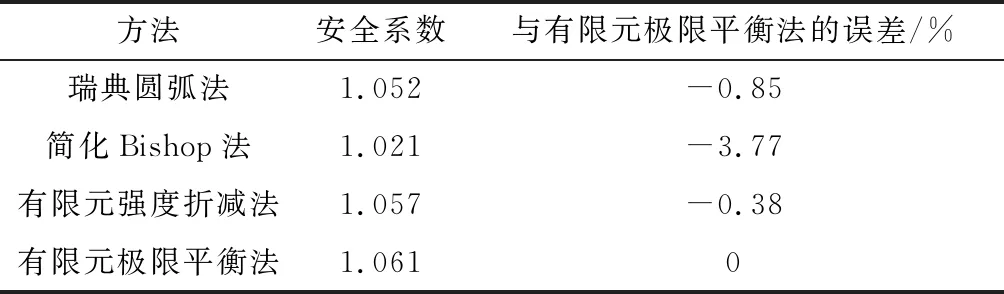
表1 安全系数比较Table 1 Comparison of safety factors
3.2 土压力分析
某混凝土重力式挡土墙高H=3 m,弹性模量E=20 GPa,泊松比v=0.2。墙后为干砂,弹性模量E=50 MPa,泊松比v=0.3,内摩擦角φ=37°,黏聚力c=0 kPa,重度为17 kN/m3。假定墙体为理想的刚性体,不会产生破坏。
基于RANKINE土压力理论得到的主动土压力为19.125 kPa,滑动面破裂角为63.5°,墙后土体在该主动土压力作用下处于极限平衡状态,即沿该滑动面的安全系数为1.0。 为了便于展开临界滑动面的搜索,在新的有限元计算模型中,撤去墙体结构,依据理论土压力大小和分布形式对墙后土体施加水平梯度载荷及重力载荷,其中主动土压力大小和分布依据RANKINE土压力理论计算得到,底部为固定约束,右边界为水平简支约束,计算模型见图7。
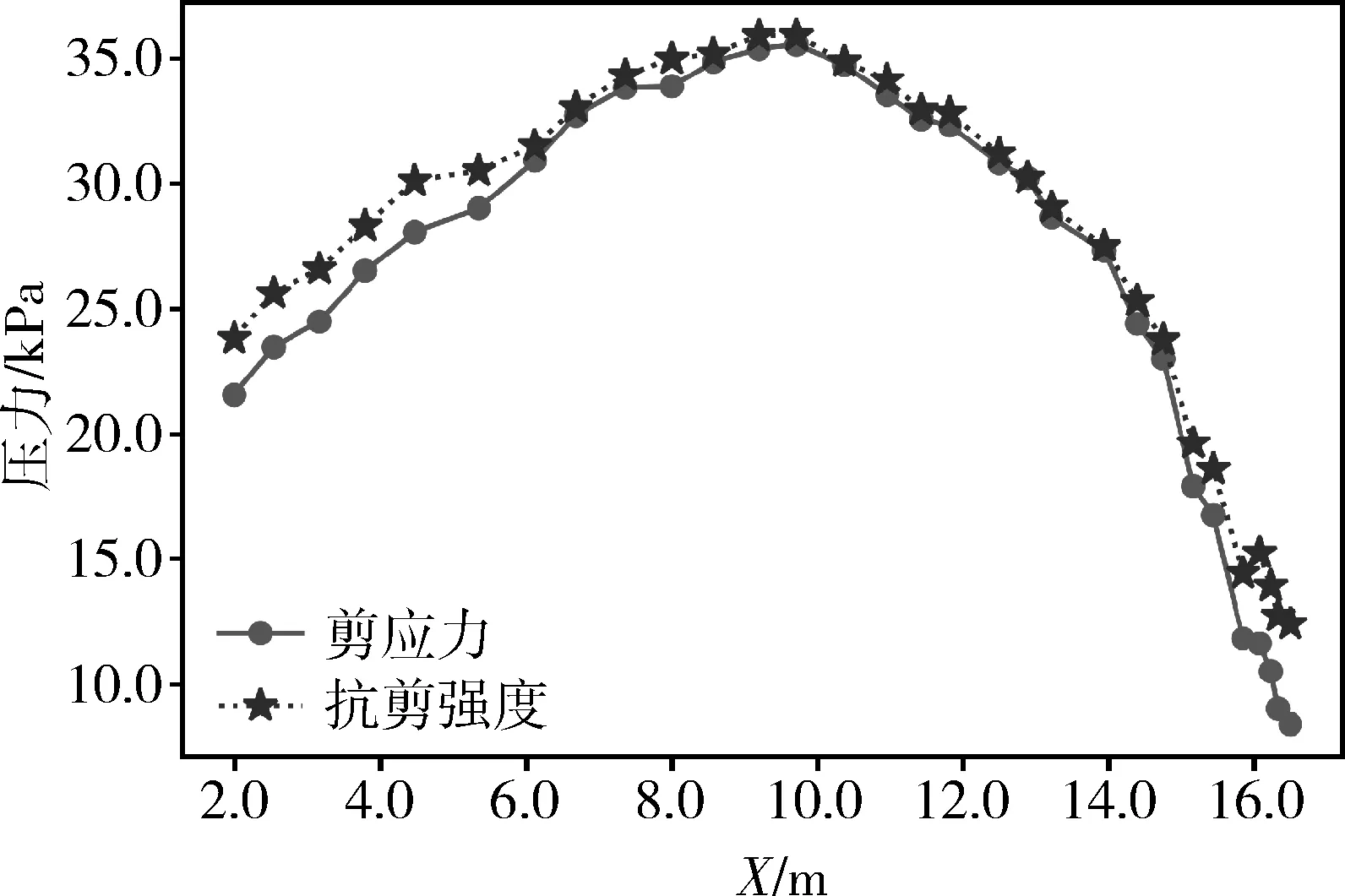
图5 临界滑动面上剪应力和抗剪强度分布Fig.5 Shear stress and shear strength distributionon the critical sliding surface
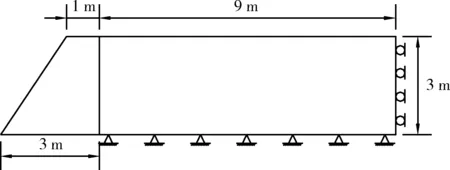
图6 重力式挡土墙结构示意图Fig.6 Schematic diagram of gravity retainingwall structure

图7 有限元计算模型Fig.7 Finite element calculation model
图8为局部与整体稳定性分析结果,从图8中可以看出局部破坏区域形状接近楔体,并贯穿整个填土,说明土体处于极限平衡状态,符合主动土压力特征。利用有限元极限平衡法计算程序搜索得到的最危险滑动面趋近于直线,安全系数为1.012,滑动面与水平方向夹角接近63.5°,与RANKINE土压力理论的滑裂面方向基本一致,但是临界滑动面端点并非位于墙角处,可能是底部约束影响墙角处的应力场导致的。

图8 计算得到的局部破坏区与临界滑动面Fig.8 Calculated local failure area and critical sliding surface
图9为有限元极限平衡法计算得到的临界滑动面上土体的剪应力和抗剪强度分布情况。由图9可知,在挡土墙墙角附近,土体虽承受较大的水平压力作用,但其沿临界滑动面的剪应力并不是最大的。整体而言,土体沿滑动面的剪应力与抗剪强度相差不大,表明土体失稳,沿滑动面达到极限平衡状态。

图9 临界滑动面上剪应力和抗剪强度分布Fig.9 Shear stress and shear strength distribution onthe critical sliding surface
3.3 地基承载力分析
采用刘士乙[15]的算例,某均质地基深15 m,宽30 m,弹性模量E=30 MPa,泊松比v=0.3(图10)。 土体容重为12 kN/m3,内摩擦角φ=10°,黏聚力c=10 kPa,地基中部作用有2 m宽的均布载荷P分别为40 kPa、60 kPa、75 kPa、85 kPa,计算地基在不同载荷作用下的局部破坏区。
图11为有限元极限平衡程序在不同载荷下得到的局部破坏区。由图11可以看出,在载荷作用下,地基主动区下方的土体首先发生剪切破坏,然后破坏区逐渐增大并向土体两侧扩展,最终载荷为85 kPa时局部破坏区贯穿至地基表面。该算例应用PRANDTL理论计算得到的地基承载力为82.8 kPa,与有限元极限平衡法得到的结果差别不大。分别向地基两侧搜索,有限元极限平衡法计算程序得到的两条临界滑动面汇总如图12所示,安全系数平均为1.017,与刘士乙[15]得到的临界滑动面基本一致。
3.4 尾矿库稳定性分析
图13是采用多管放矿上游式筑坝的尾矿库。 初期坝采用库区开采的岩石筑坝,坝顶标高为135.0 m,上游坡与下游坡坡比均为1∶2,坝顶宽6.0 m。 子坝采用尾砂筑坝,外坡为1∶5,尾矿库最终堆筑标高为250 m。尾矿坝各部分材料参数见表2。

图10 地基结构示意图Fig.10 Schematic diagram of foundation structure
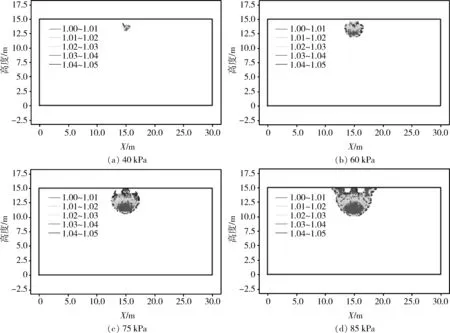
图11 不同荷载下地基的局部破坏区Fig.11 Local failure zone of foundation under different loads

图12 计算得到的临界滑动面Fig.12 Critical sliding surface calculated byfinite element limit equilibrium method
对图13所示的断面,采用有限元程序进行有限元应力应变计算,可以得到坝体计算区域的应力分布。为便于计算,取尾矿库尺寸的十分之一进行建模。有限元计算模型如图14所示。启用自主开发的岩土结构稳定分析的有限元极限平衡法计算程序,自动读入有限元计算得到的应力场信息,在操作界面输入有限元极限平衡法分析所需的参数。分析结果表明,尾矿库内未出现局部破坏区域,计算得到的整体临界滑动面及其安全系数如图15所示。图16为采用BISHOP法和瑞典圆弧法计算得到的临界滑动面及其安全系数,图17为有限元强度折减法计算终止时的增量位移图。由图15~图17可以看出,基于有限元极限平衡法得到的临界滑动面与其他方法计算得到的临界滑动面位置基本一致。
表3给出了各种不同方法计算得到的安全系数。从表3可以看出,4种计算方法得到的临界滑动面差别不大,基于有限元应力场计算得到的安全系数略大于传统极限平衡法计算的结果,整体安全系数较高。改变荷载工况,可以分析坝体局部和渐进破坏过程,由此可以预估破坏区域和滑动危险性。

图13 尾矿坝示意图Fig.13 Sketch of the tailings dam

表2 尾矿坝材料参数Table 2 Material parameters of tailings pond
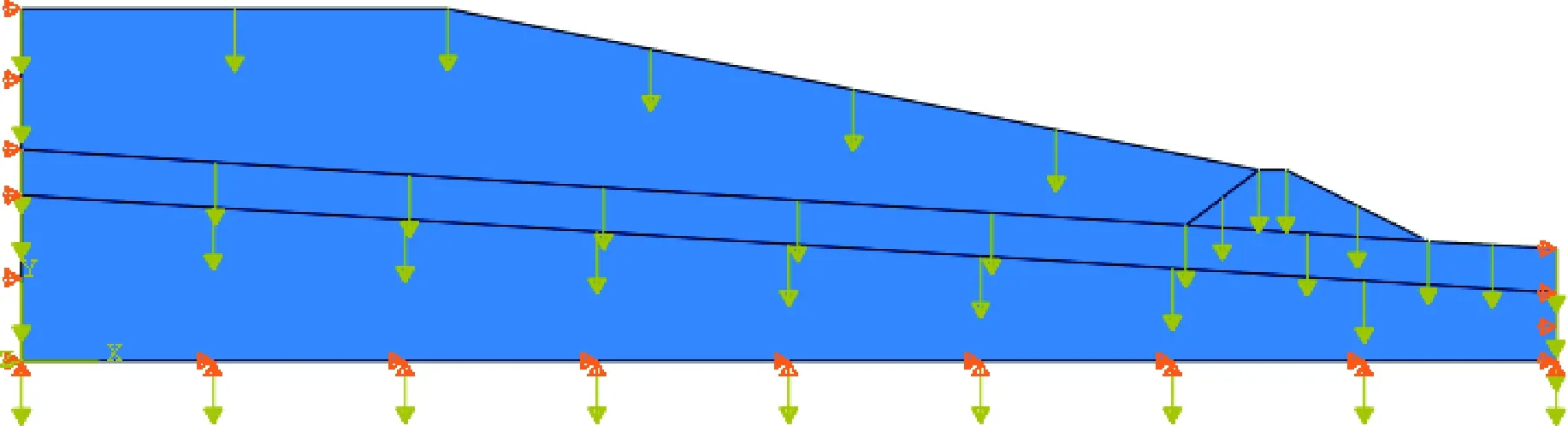
图14 有限元计算模型Fig.14 Finite element calculation model

图15 计算参数输入和计算结果显示Fig.15 Parameter input and calculation results display

图16 BISHOP法和瑞典圆弧法得到的临界滑动面及其安全系数Fig.16 Critical sliding surface and safety factor obtained by BISHOP and Ordinary method
4 结 论
本文对传统极限平衡理论进行了扩展,在讨论土体内一点的极限平衡状态与土体沿着任意曲面的极限平衡状态的基础上,阐释了以曲面为底的任意土体沿着曲面达到极限平衡的充分必要条件,由此定义了土体沿(整体或局部)曲面的安全系数,将此理论用于土体学三大经典问题的分析,并与其他理论得到的结果进行对比,得到以下结论如下所述。

图17 有限元强度折减法计算终止时的增量位移图Fig.17 Incremental displacement diagram at the end of the FEM strength reduction
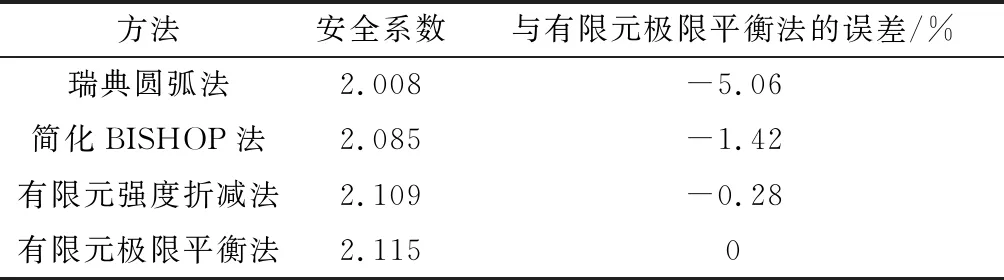
表3 安全系数比较Table 3 Comparison of safety factors
1) 对于边坡稳定性问题,有限元极限平衡法计算得到的临界滑动面上土体剪应力与抗剪强度分布符合实际特征,其位置和安全系数与瑞典圆弧法、简化BISHOP法、有限元强度折减法得到的结果相差不大。
2) 对于挡土墙问题,将RANKINE理论计算得到的主动土压力直接施加至墙后土体用于有限元计算,有限元极限平衡法得到的局部破坏区形状接近楔形体,并贯穿整个填土区,搜索得到的临界滑动面接近于直线,与RANKINE土压力理论的滑动面方向一致,计算得到的安全系数接近于1。但是由于底部约束的影响,临界滑动面端点不在墙角处,而是位于墙角上方不远处。
3) 对于地基承载力问题,采用逐渐增加地基载荷的方式,得到了地基的渐进破坏过程。结果表明,在极限载荷作用下,地基土体RANKINE主动区下方土体首先发生剪切破坏,然后破坏区逐渐增大,最终贯穿至地基表面,得到的极限载荷与PRANDTL理论计算的结果很接近。

