基于主成分分析-物元可拓的地铁盾构施工风险评价

王建波，秦 娜，黄文静，张 薇，王政权，张 娜

(1.青岛理工大学管理工程学院，青岛 266520； 2.山东省高校智慧城市建设管理研究中心(新型智库)， 青岛 266520)

引言

随着城市化进程的推进，城市人口急剧增长，传统的公共交通工具已经难以满足人们日益增长的交通需求。地铁以其高效、快速的优势成为缓解城市交通拥堵的重要基础设施。截止2019年，全国地铁运营线路长度达5 181 km，同比2018年增长19.0%，占城市轨道交通运营线路总里程的76.8%。盾构法在城市地铁施工中应用广泛，其施工总长占据了城市轨道线路总长的50%～70%[1]。然而，由于地下工程建设具有施工周期长、技术复杂、不可预见风险因素多等特点，近年来国内地铁盾构施工事故频发，严重威胁公共安全。评估地铁盾构施工风险是进行风险管理的第一步，只有科学合理的评估地铁盾构施工风险，确定关键的风险因素，并据此进行相应的风险控制措施，才能够有效控制或减小盾构施工风险，从而减少类似事故的发生。因此，对地铁盾构施工风险评估进行研究具有重大的现实意义。

国内外学者在地铁盾构施工风险领域均取得了丰硕的研究成果，主要包括建立评价指标体系和构建评价模型两个方面。在建立地铁盾构施工风险评价指标体系方面，Einstein[2]深入分析了隧道风险因素；Tonon等[3]利用随机理论和模糊理论研究了隧道工程建设风险。这些文献为盾构施工风险因素研究奠定了理论基础，但忽略了施工风险必要的筛选过程，大多单纯依靠指标含义、个人或专家经验建立的施工风险因素清单，主观性较强过于随意。在构建地铁盾构施工风险评价模型方面，层次分析法[4]、熵度法[5]、模糊综合评价法[6]、贝叶斯网络法[7]等方法得到了广泛应用，但层次分析法主观性较强，熵度法对数据的依赖性较强，模糊综合评价法分辨率低导致计算精度不高，贝叶斯网络法训练数据集中属性冗余，这些都使得模型计算结果不够准确。此外，洪文霞等[8]运用DEMATEL和vague法构建了盾构施工风险评价模型，但vague法对于距正负理想解距离相等的方案无法给出正确评价；胡长明等[9]建立了风险可拓评估模型，对地铁盾构施工风险进行了评估，但未考虑评价指标的模糊性。

基于此，首先运用主成分分析法建立了地铁盾构施工风险评价指标体系，通过降维使所得的指标体系更加科学可靠；同时考虑准则权重和次序权重各自的优缺点，结合有序加权平均(Ordered Weighted Averaging，简称OWA)算子法和简单关联函数法确定评价指标的综合权重，使得权重结果更加客观准确；然后考虑到专家评价信息的偏好性，引入三角模糊数和专家动态权重，并在此基础上构建物元可拓评价模型，实现了对地铁盾构施工风险的综合评价。最后，对青岛地铁1号线安安区间应用所建模型进行验证，以期提高盾构法施工地铁项目的风险管理水平。

1 地铁盾构施工风险评价指标体系的构建

地铁盾构施工风险影响因素众多且复杂，采用主成分分析法对各个风险因素进行权重测算，以筛选掉次要成分的干扰，同时排除各风险因素之间的相关性，并抽取主要指标构建地铁盾构施工风险评价指标体系。

1.1 确定影响因素初始清单及评分等级

首先，广泛阅读地铁盾构施工风险相关参考文献[10-15]，依据科学全面的原则，归纳总结出38个地铁盾构施工风险影响因素；然后，采用德尔菲法对地铁盾构领域的专家进行问卷调研(专家信息见表1)，进一步整理筛选得到包含30个风险影响因素的初始清单。

表1 专家组成员背景信息

按照各因素对地铁盾构施工风险管理的影响程度划分评分等级(表2)。邀请上述专家依据表2对风险影响因素进行评分，得到专家初始评价矩阵。

表2 影响因素评分标准

1.2 主成分分析

利用MATLAB软件对专家初始评价矩阵进行数据处理，得到相关系数矩阵R的特征值、方差贡献率以及累计方差贡献率，并根据累计贡献率原则确定主成分数目[16]。计算结果显示，前8个主成分的方差累计贡献率已达到87.424%，因此，这8个主成分可作为主成分反映原始指标所包含的信息。

根据主成分评价函数模型Fh=αh，1Y1+αh，2Y2+…+αh，30Y30(h=1，2，…，8)以及基础贡献率推出主成分的表达式[16]。指标的相关系数绝对值越大，则其对主成分的相关性越大。利用MATLAB软件得到相关系数矩阵特征向量的绝对值，如表3所示。其中，Yl(l=1，2，…，30)为原始指标；αh，l为主成分Fh中原始指标Yl对应的成分得分系数。

依据表3将影响因素重新分类。对于主成分F1，相关系数α1，30，α1，27，α1，19，α1，18，α1，9，α1，8，α1，6分别为0.314 7，0.314 4，0.313 4，0.287 8，0.280 7，0.271 7，0.268 9，相对于其他相关系数较大，因此，将Y6，Y8，Y9，Y18，Y19，Y27，Y30作为主成分F1的主要指标。这七个指标分别是盾构机及配套设备选型、盾构机刀盘刀具磨损情况、管片运输风险、盾构机管片拼装系统故障、机器设备日常维修状况、进场设备优良率、盾尾密封装置是否失效，反映了机械设备管理。同理可得，其他主成分分别反映了施工环境、人员标准化操作、施工技术、组织制度及安全控制措施、材料管理、施工防护技术、人员基本素质。

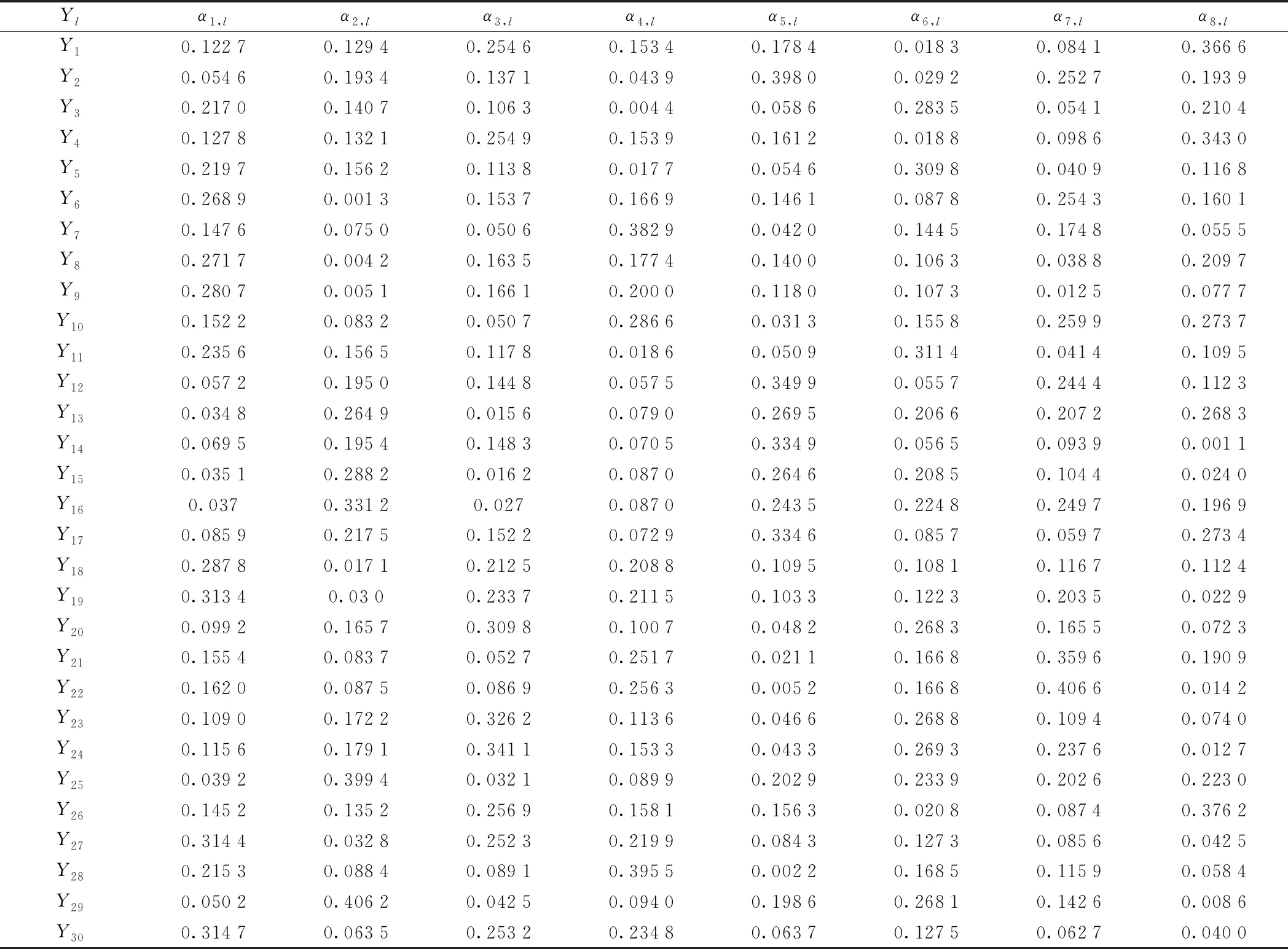
表3 相关系数矩阵R特征向量的绝对值

1.3 构建施工风险指标体系

根据以上主成分分析，并结合工程实际情况，将各主成分整理归类。F3，F5，F8为人员基本素质及组织管理，记为C1；F4，F7为施工技术，记为C2；F1，F6为机械设备及材料管理，记为C3；F2为施工环境，记为C4。据此构建地铁盾构施工风险评价指标体系，见表4。

表4 地铁盾构施工风险评价指标体系

2 地铁盾构施工风险评价指标综合权重的确定

目前，研究指标权重通常包括准则权重和次序权重[17]。准则权重考虑了指标间的相对重要性，但是忽略了指标间等级重要性(次序)对评价结果的影响，确定准则权重的方法有熵权法、AHP等。次序权重则能够考虑指标因子在次序上对评价结果的影响，求取次序权重方法如OWA算子等。准则权重和次序权重各有优劣，因此，综合考虑相对重要性(准则权重)和等级重要性(次序权重)对结果的影响，即结合OWA算子和简单关联函数法来确定指标权重，以提高结果的精确度。

OWA算子由Yager提出[18]，该方法通过有序加权平均算子计算各指标的次序权重，以解决评价过程中指标因子在等级重要性上对评价结果影响这一问题，有效削弱了主观因素对评分结果的不利影响，使得评分结果相对科学，具体步骤如下。

2.1 AHP-OWA确定指标权重

(1)邀请评分专家Ed={E1，E2，…，EN}采用层次分析法确定地铁盾构施工风险评价指标的初始权重，记作初始权重矩阵D=(dgie)n×N。其中，dgie表示专家Ee(e=1，2，…，N)通过AHP确定的一级指标Cg下二级指标Cgi的权重，且e=1，2，…，N;g=1，2，…，m;i=1，2，…，n。

(2)对初始权重矩阵的第i行数据进行降序排列，得到AHP得分新数据组：zgi，0，zgi，1，…，zgi，N-1(zgi，0≥zgi，1≥…≥zgi，N-1)。

(3)通过位置赋权确定相对权重，并对权重进行修正得到AHP-OWA次序权重。根据排列组合数对指标Cgi的AHP得分新数据组进行赋权，可得赋权向量βgi，k+1。利用赋权向量βgi，k+1对AHP得分新数据组进行加权，得到指标Cgi的绝对权重，进而求得相对权重vgi。指标权重公式如下

(1)

(2)

2.2 简单关联函数法确定指标准则权重

简单关联函数法是建立在可拓学理论上的一种客观赋权法[19]。它考虑了指标间的相对重要性，能够定量地描述可拓域中的元素具有某一性质的程度及其变化，更具体地刻画类内的程度区别，使得权重取值更加灵活可靠。具体步骤如下。

(1)邀请专家对风险因素的重要程度进行评分，取专家群体评分的平均值可得专家评分Xgi。评分规则如下：将指标划分为非常重要、比较重要、一般重要、不重要、非常不重要5个评价等级，分别对应分值范围[0.8，1)、[0.6，0.8)、[0.4，0.6)、[0.2，0.4)、[0，0.2)。由于评价等级的取值范围都为有限区间，故利用如下简单关联函数对评估指标值Xgi与各评估等级的关联度进行求解。若正域有限区间X∈〈a，b〉，点Xgi满足条件：

Xgi∈(-∞，+∞)，M∈X，

则有以下3种情况。

①当M=a时，则有

(3)

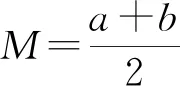
(4)

③当M=b时，则有

(5)

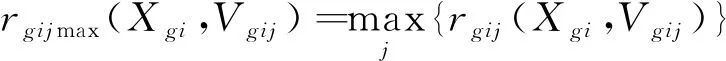
(6)

式中，r(Xgi，Vgij)是评估指标值Xgi与各级评估等级的简单关联函数；经典域Vgij=〈agij，bgij〉为评价指标集Cgi(i=1，2，…，n;g=1，2，…，m)关于评价等级j(j=1，2，…，f)所规定的量值范围。

(2)计算评估指标值Xgi的简单关联函数。若指标数据落入的级别区间越大，对待评对象越不利，则该指标应赋予越大的权值。

(7)

否则，指标数据落入的级别区间越大，该指标应赋予越小的权值。

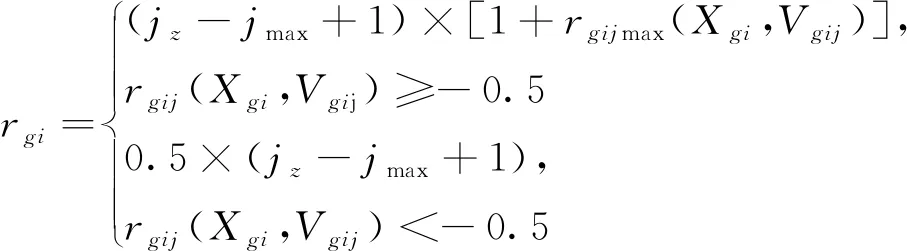
(8)

式中，rgi是评估指标Cgi的简单关联函数；jz为划分等级总数；jmax为待评物元指标的样本值落入等级，其值越大说明该指标对待物元的限制性越强。

(3)计算二级指标权重ugi。

(9)

2.3 综合权重的确定

将OWA算子法和简单关联函数法求解出的指标权重，通过线性加成法以求得指标的综合权重，使得评分结果更加客观准确。综合权重ωgi的计算公式为

ωgi=αugi+(1-α)vgi，

(10)

式中，α的取值根据准则权重和次序权重两者偏差平方和最小的原则来确定，公式如下

(11)

3 基于物元可拓的地铁盾构施工风险评价模型的构建

3.1 基于三角模糊数-专家动态权重确定指标评估值

表5 三角模糊数语义转化

①将三角模糊数标准化。

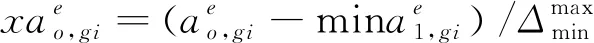
(12)

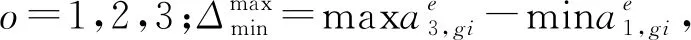
②将左边值和右边值标准化。

(13)

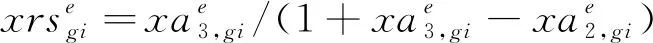
(14)

③计算去模糊化后的清晰值。

(15)

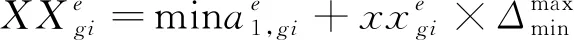
(16)

(17)

(18)

(19)

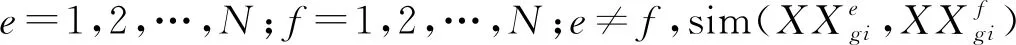
3.2 建立可拓评价模型

(1)确定二级指标的经典域、节域与待评物元。

①确定二级指标Cgi的经典域。

式中，g=1，2，…，m;i=1，2，…，n，j(j=1，2，…，f)为评价等级。经典域Vgij=〈agij，bgij〉为评价指标集Cgi关于评价等级j所规定的量值范围。

②确定二级指标Cgi的节域。

(21)

式中，节域VgiU=〈agi1，bgif〉为评价指标集Cgi关于全部评价等级J={j1，j2，…，jf}所规定的量值范围。

③确定二级指标Cgi的待评物元。

(22)

式中，P为待评对象；xgi为待评对象P关于Cgi的量值。

(2)确定待评事物二级指标Cgi关于各个等级j的关联度。

(23)

式中，ρ(xgi，Vgij)=ρ(xgi，〈agij，bgij〉)=|xgi-(agij+bgij)/2|-(bgij-agij)/2为待评物元指标值与经典域之间的距离；ρ(xgi，Vgij)=ρ(xgi，〈agi1，bgif〉)=|xgi-(agi1+bgif)/2|-(bgif-agi1)/2为待评物元指标值与节域之间的距离；kj(xgi)为xgi的关联函数。

(3)计算一级指标对应各个等级j的关联度。

(24)

式中，ωgi为综合权重法计算出来的二级指标权重值。

(4)计算待评事物P关于各个等级j的关联度。

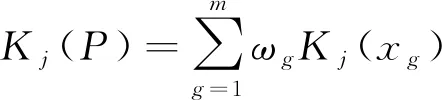
(25)

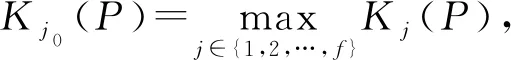
(5)级别变量特征值j*的确定。

(26)

(27)

式中，j*可以表明评价结果偏向哪一级别的程度，其整数部分表示所处的评价等级，小数部分表示关于相邻两等级的偏向性。

4 案例分析

青岛地铁1号线全长60 km，穿越胶州湾连接青岛主城区和黄岛城区，是贯通青岛市南北的快速轨道交通走廊。地铁1号线西海岸新区安安区间(安子东站至安子站)全长921.7 m，盾构机从安子东站始发，沿新港山路及长江东路掘进，到达安子站后接收并吊出。安安区间地质复杂，车站距海边约200 m，地下水位为地面下3.6 m，盾构施工面临诸多挑战。邀请设计、参建单位专家及地铁工程领域行业专家对安安区间盾构法施工风险进行评估。

4.1 模型应用

(1)确定指标权重值

利用Matlab软件根据公式(1)、公式(2)计算可得次序权重值，根据公式(3)～公式(9)计算可得准则权重值，构建拉格朗日函数对公式(11)进行求解可得，α=0.5。再借助公式(10)求解指标的综合权重，见表6。

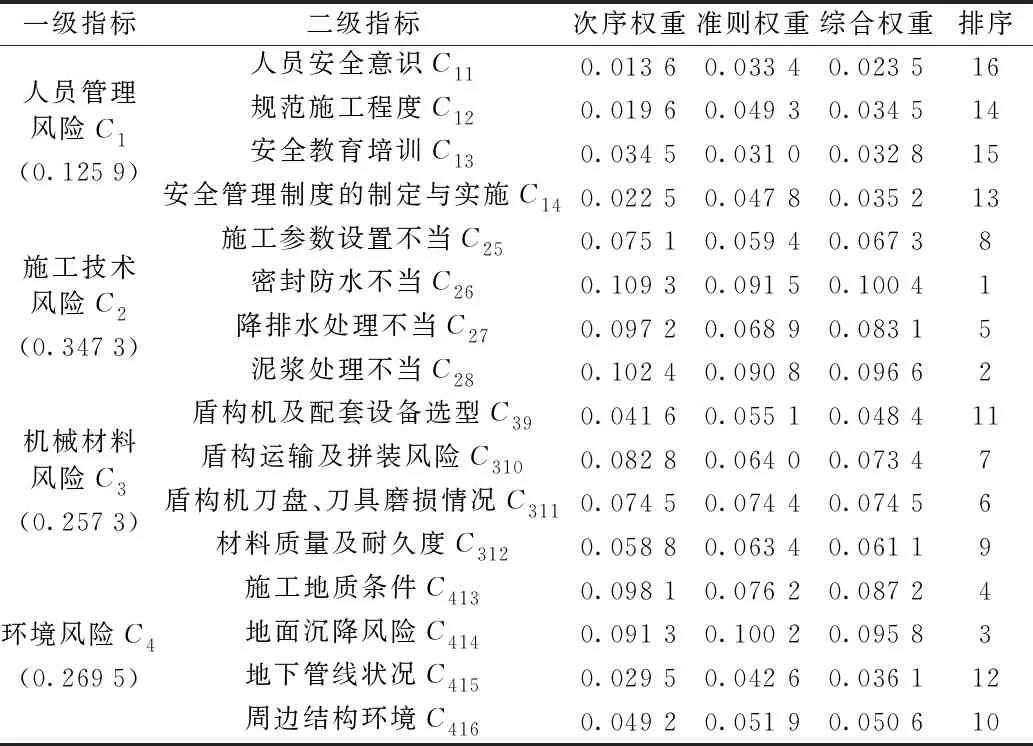
表6 风险指标权重计算结果

(2)确定经典域、节域以及待评对象指标值。

以一级指标“人员管理风险”为例，专家打分见表7。结合项目实际情况，运用分级标准量化的方法确定各个指标的经典域、节域，并根据专家对风险指标的评估以及公式(12)～公式(19)，利用MATLAB软件计算可得评估指标值，见表8。其中，指标的分级标准量化过程以二级指标“人员安全意识”为例，取值规则为：生产人员安全意识非常高取值[0，0.2]；较高，取值[0.2，0.4]；一般，取值[0.4，0.6]；较低，取值[0.6，0.8]；非常低，取值[0.8，1]。

表7 待评物元指标值评分

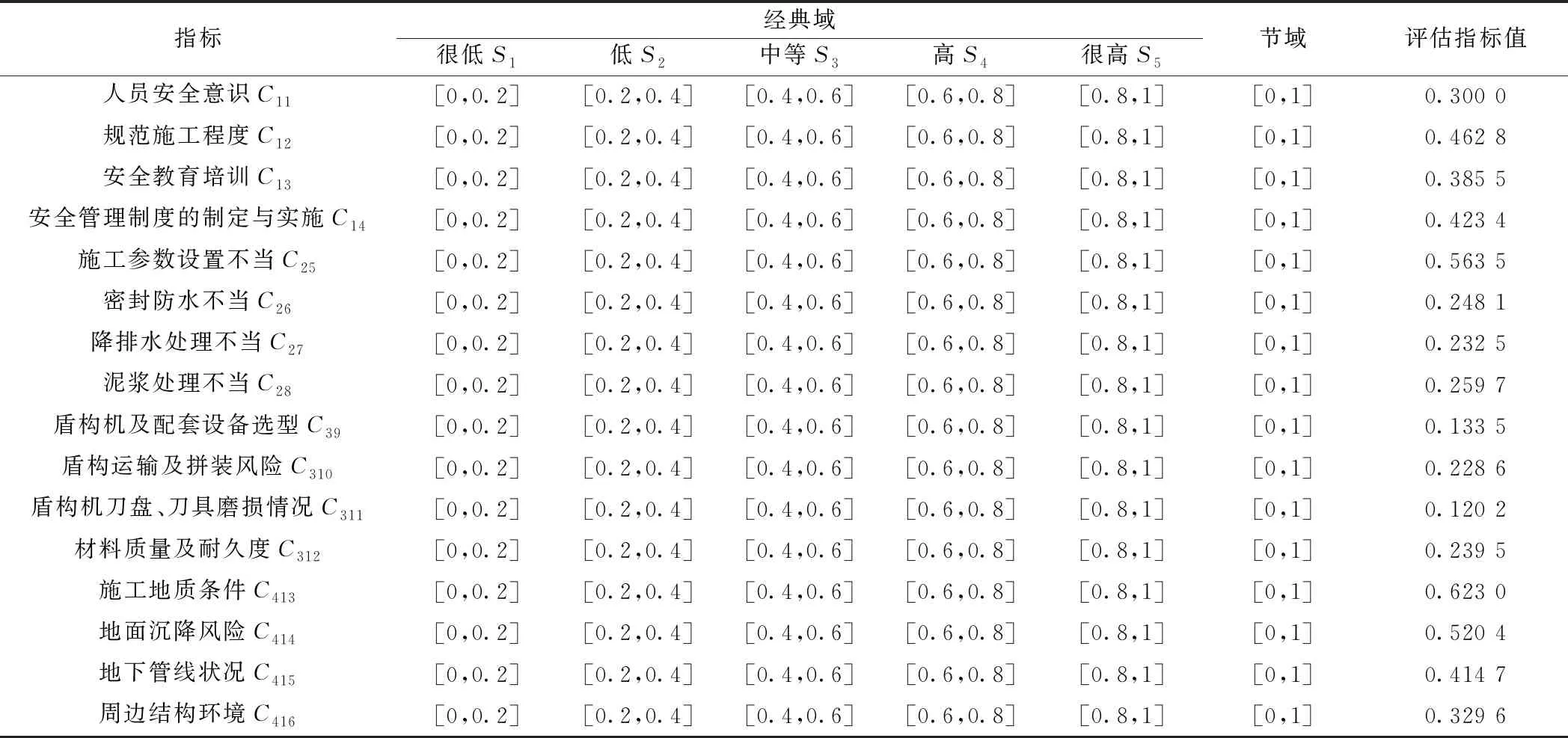
表8 经典域、节域、评估指标值

(3)可拓综合评价

根据公式(23)～公式(25)求解得到一级指标、二级指标关于各个等级的关联度，计算结果见表9。由公式(26)、公式(27)求解级别变量特征值可得，j*=2.459。

表9 关联度计算结果

4.2 结果分析

由表9可知，青岛地铁1号线安安区间盾构施工风险的综合评价等级为二级，即低风险。由级别变量特征值j*=2.459可知，该地铁项目盾构施工风险等级偏向j2(中等风险)，即向更危险方向转变。项目风险监测部门实测风险等级为Ⅱ级，评估结果与实测风险等级一致，验证了所建模型的可行性和有效性。另外，将本文与文献[8，12]的评估结果进行对比分析，文献[8]与文献[12]的评估结果分别为“低风险”、“较低风险”，本文评估结果为低风险偏向中等风险转变，评估结果的一致性证明了所建模型的科学准确性。所建模型给出了风险等级及风险偏向趋势，具有更强的辨识度，有利于未来风险管理。

从指标权重结果来看，一级指标技术风险和环境风险的权重较大，二级指标密封防水不当、泥浆处理不当、施工地质条件和地面沉降风险的权重较大。另外一级指标与各等级的关联度显示，技术风险和环境风险所属的风险等级较高。结合该项目实际情况，安子东站是安安区间盾构的始发点，该车站距海边约200 m，地下水位位于地面以下3.6 m，周边建筑物、管线众多，如此复杂的地质环境必然对密封防水、泥浆处理与降排水处理等施工技术工作提出严格要求。本次评估结果与项目现场实际情况相符，再次验证了所建模型的科学有效性。

针对评估结果提出以下建议措施：项目盾构法施工前期，需做大量的现场地质勘测、考察工作，同时组织参建单位和特邀外部专家召开研讨会，对设计方案和施工工艺进行探讨把关，以便更好地应对未来风险；盾构施工过程中，需实时监测关键风险并采取有针对性的控制措施，以便做好风险管理工作，例如实时监测水位变动，及时进行降排水处理，优化同步注浆配比，做好密封防水工作，信息化监控有效控制盾构掘进参数，并优化最佳掘进参数，规范技术操作，严格把控管片粘贴和拼装质量等。

5 结论与建议

通过建立地铁盾构施工风险评价指标体系，结合OWA算子和简单关联函数法确定了指标权重，基于物元可拓理论构建了地铁盾构施工风险评价评价模型。并以青岛地铁1号线安安区间实例验证了所建模型的可行性和有效性。研究结论总结如下。

(1)采用主成分分析法对地铁盾构施工风险影响因素进行降维处理，并结合项目实际情况，建立了地铁盾构施工风险评价指标体系，确保了指标体系的科学合理性。

(2)针对指标权重，综合考虑了准则权重和次序权重的优劣，采用OWA算子法和简单关联函数法相结合的综合权重法确定了指标权重，以增加结果的准确性。

(3)针对盾构施工风险因素的模糊性、不确定性及专家评价的偏好差异性，引入三角模糊数和专家动态权重进行处理，并建立了相应的五级语义转化集，以增加评价信息的完整性和准确性。

(4)借助物元可拓理论解决风险因素评级的矛盾性，构建物元可拓综合评价模型对地铁盾构施工风险进行评价，以增强结果的准确性。该模型可为地铁盾构施工提供较为精确的评价信息，同时也可以拓展到其他领域，具有一定的借鉴意义。

地铁盾构施工风险因素众多且复杂，未来可深入研究具体风险指标值的变化对于目标的影响程度。此外，本次主要研究了地铁盾构施工风险评价问题，对盾构施工风险的应对措施研究不足，后续可对此深入研究，以推动我国地铁项目盾构法施工的发展。