基于线性自抗扰的齿轮传动涡扇发动机控制
刘云霄,胡忠志,王继强
(南京航空航天大学能源与动力学院,南京 210016)
0 引言
涡扇航空发动机是极其复杂的非线性系统,运行工况与外界环境多变,存在各种各样的干扰。目前国内还未见专门对大涵道比涡扇发动机中的各种干扰和控制的公开研究报道。可实际上发动机工作在复杂多变且恶劣的环境中,如果建模控制等研究忽略各种干扰,只是比较发动机在确定模型下的各类控制问题显然是不够的。PW 公司花费近20 年时间和10 多亿美元研发的齿轮传动涡扇(GTF)发动机相对于现役的传统涡扇发动机,油耗降低15%,维护成本降低20%,噪声降低75%,污染物排放降低50%[1-2]。中国针对GTF 发动机的建模技术研究还不多,张登稳等[3]根据已有的小型齿轮传动涡扇发动机DGEN380试验平台,简单建立了GTF发动机部件级模型,但其模型结构较为简单。建立精确实用的GTF发动机模型对研究干扰模型和控制算法非常重要。
发动机的系统干扰按干扰来源分为外部干扰和内部干扰。外部干扰包括大气湍流、电磁、发动机功率提取以及引气干扰等;内部干扰包括燃油泵、传感器等部件受环境影响的干扰、涡轮或压气机部件健康参数蜕化等。从建模原理可概括为系统内部无法建模的动态过程、未知的系统参数、外界的环境变化、传感器或执行机构的噪声等[4]。传统PID(Proportion In⁃tergration Differentiation)控制方法对干扰的抑制能力较弱。自抗扰控制(Active Disturbance Rejection Con⁃trol,,ADRC)方法可解决具有大范围复杂结构不确定系统的控制方法[5-6]。之后LI 等[7]又提出将自抗扰控制方法简化后的线性自抗扰控制(LADRC)方法,将部分控制结构线性化,解决了ADRC 参数过多且调节方法无规律可循的问题,LADRC 也可以达到较好的控制效果,不仅节省了不必要的工程上应用的时间,还利于此方法的普及与应用。
本文采用LADRC 方法实现发动机抗扰的功能,对比研究PID 与LADRC 控制器的抗干扰效果并在硬件在环(Hardware In-the-Loop,HIL)仿真平台上进行验证。
1 带有干扰的GTF发动机MBD建模
本文将传统部件级模型建模方法应用于某型GTF发动机稳态部件级模型建模中,基于流量法开展了GTF发动机稳态性能建模技术研究。
1.1 GTF发动机建模
本文研究对象为1 台大推力、双转子、混合排气、喷口面积不变的GTF发动机,主要由进气道、风扇、减速齿轮箱、高压压气机、燃烧室、高压涡轮、低压涡轮、内涵喷管和外涵喷管组成。减速齿轮箱的传动比为3.1[8]。发动机结构如图1所示。
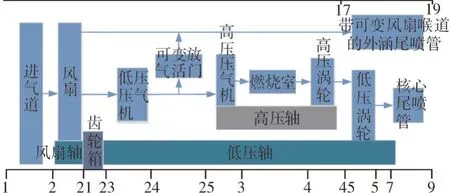
图1 GTF发动机仿真模型
1.2 基于模型的设计方法
基于模型的设计(Model Based Design,MBD)方法是利用计算机建模仿真技术,快速完成嵌入式产品等产品开发过程中核心算法的开发和验证工作。利用模型的方法和自动代码生成技术可以快速完成产品开发中的逻辑功能、处理算法;利用模型方法构造出被控对象,可以方便、快捷、大量重复地进行产品控制效果的验证工作。MBD 方法具有很多优点,如其图形化界面简单、操作简洁、软件能自动生成高质量代码、代码或模块容易封装且具有良好继承性保密性,与硬件在环平台对接良好。目前,MBD 研发方法在汽车电子领域[9]取得良好效果,未来MBD 技术在航空航天等复杂控制系统研发领域将会有广阔的应用前景[10]。
1.3 静态方程
1.3.1 风扇、压气机及涡轮模型
风扇与压气机都是气体压缩部件,涡轮是气体膨胀部件,其公式大都相同,所以在此仅介绍风扇建模。风扇的特性通过GasTurb 软件获取其通用特性图,计算时通过等换算转速线和特性曲线变量线(β线),采用差值方法求得压气机运行点数据。特性图计算时,压比Pr、换算转速Nc、换算空气质量流量Wc和压气机效率eff之间关系定义为
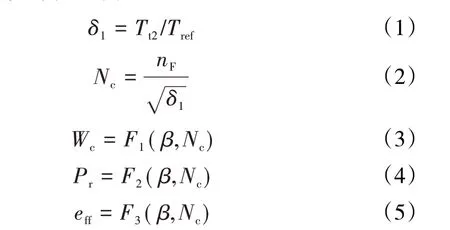
式中:δ1为折合总温;Tt2为风扇进口温度;nF为风扇转速,通常标准天气流总温Tref=288 K,总压Pref=101.325 kPa;Fi为插值函数。
1.3.2 燃烧室模型
燃烧室的功能是将高压空气喷入燃油燃烧,利用燃气的热能进入涡轮膨胀作功。
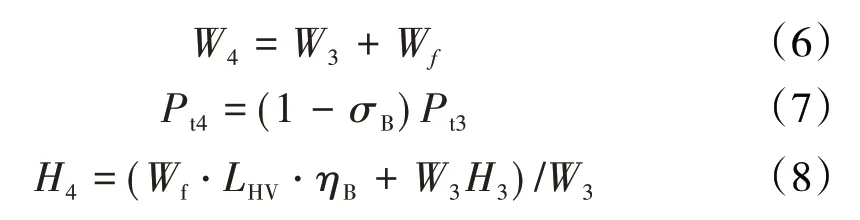
式中:W4为燃烧室出口气体质量流量,kg/s;W3为燃烧室入口气体质量流量,kg/s;Wf为燃料质量流量,kg/s;LHV为燃料低热值,kJ/kg;σB为燃烧室总压损失系数;ηB为燃烧室燃烧效率;H3为燃烧室出口总焓值。
1.3.3 尾喷管模型
涡扇发动机尾喷管的作用是将涡轮出口的燃气在尾喷管中继续膨胀,将燃气的部分热焓转变为动能,增大发动机出口气流的速度,也即增大发动机推力。GTF 发动机采用外涵道与核心机分开排气的方式提供推力,且二者均为纯收敛型喷管,所以具体气体参数计算方式不多叙述,主要是推力计算。
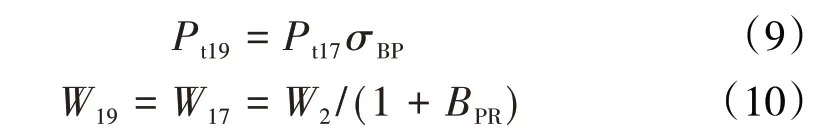
式中:Pt19和Pt17分别为19截面和17截面的总压,kPa;W19、W17、W2分别为通过19、17、2截面的流量,kg/s;BPR为涵道比;σBP为外涵总压恢复系数。
外涵道推力为
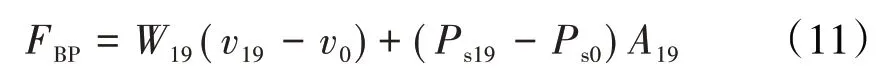
核心机推力为
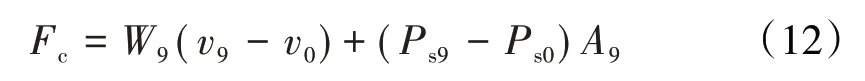
总推力为

式中:vi为i截面的气体流速,m/s;Psi为i截面的静压,kPa;Ai为i截面的面积,m2。
1.3.4 可变风扇喉道与可变放气活门模型
GTF发动机控制对象主要有燃油流量、可变放气活门(Variable Bleed Valve,VBV)和可变面积风扇喷嘴(Variable Area Fan Nozzle,VAFN)。VAFN 部件功能与尾喷管功能一样,不过核心机尾喷管是面积固定的,而外涵道的喉道面积是可以改变的。发动机通过风扇进入外涵道的气体会通过VAFN排出。VAFN通过在给定折合流量和转速的条件下保持特定的压比,使风扇在工作点有最佳的风扇性能。可变喉道风扇面积如图2所示。

图2 可变风扇喉道面积与马赫数
VBV 可以将低压压气机里的空气从出口转移到外涵道,以防止压气机失速。可变放气活门开度与马赫数关系如图3所示。
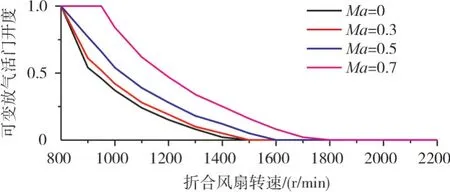
图3 可变放气活门开度与马赫数关系
相关参数计算如下
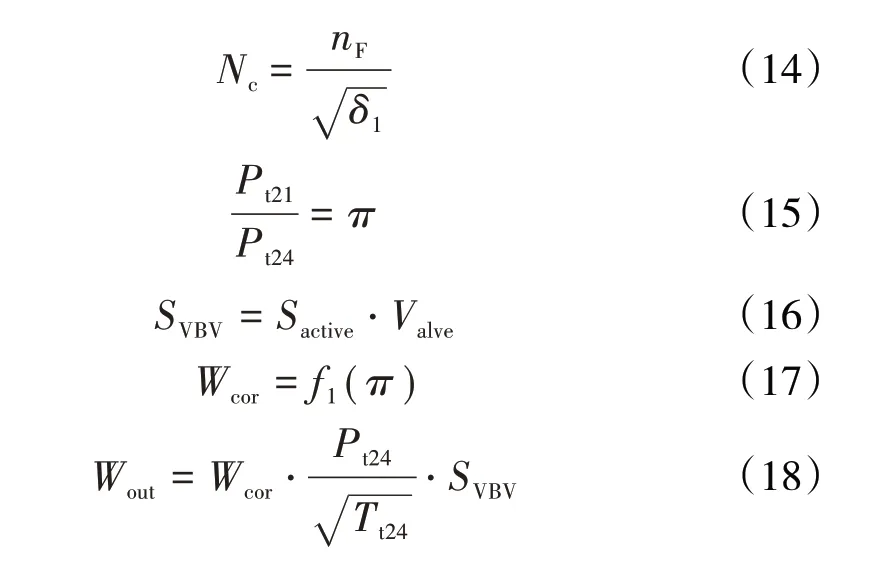
式中:π为压比;Valve为阀门的开度;Sactive为可变放气活门总面积,m2;SVBV为实际面积,m2;Wcor、Wout分别为换算流量和出口流量。
f1的换算关系如图4所示。
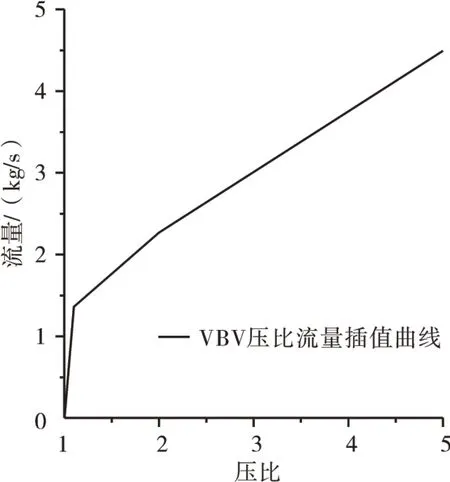
图4 VBV流量换算关系
1.3.5 转子模型
GTF发动机风扇转速与低压转速换算为

式中:nF为风扇转速,r/min;nL为低压转子转速,r/min;GR为减速齿轮箱的减速比。
齿轮箱对气体流动没有影响,主要会改变风扇轴转速和风扇传递到低压转子的扭矩。发动机处于动态时,有7组流量平衡方程。此外需要加入转子的微分方程进行加减速计算,高、低压轴的转子动力学方程为
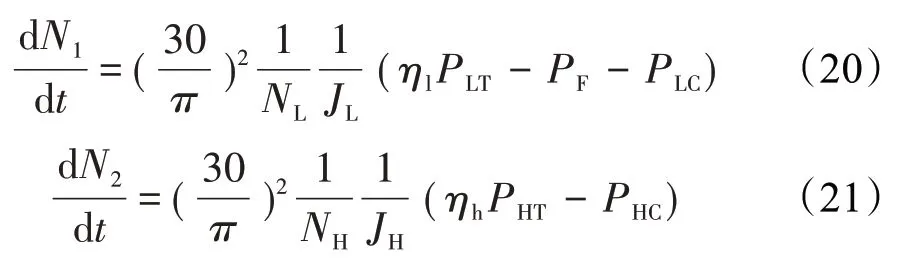
式中:JH、JL分别为高、低压轴转动惯量,kg·m2;由风扇轴、齿轮箱、低压轴耦合形成。NH、NL分别为高、低压轴转速,r/min;P为各轴的功率,kW。
1.4 稳态数据点匹配
为验证稳态模型仿真精度,选取GTF发动机若干典型稳态工况点,对比模型输出数据和试验数据。设计点参数相对误差见表1,非设计点参数相对误差见表2。
非典型呼吸道感染患者临床无特异表现,患者容易被误诊、漏诊。因此,对非典型病原体的检查显得尤为重要。采用间接免疫荧光法检测血清IgM,针对呼吸道感染非典型病原体进行检测,研究表明,运用该检测方法,9种非典型性病原体的检测灵敏度为86.2%~100.0%,特异性92.8%~100.0%,该方法方便、快捷,可广泛采用[1]。
通过对比仿真值和试验值,无论设计点还是非设计点的建模误差均小于2%,建模精度较高,证明模型具有较高的正确性和适用性。
1.5 大气湍流畸变模型
大气湍流造成进气道前气体各参数的变化,可能导致各部件内气体流动状态的不稳定,并在一定程度上导致发动机转速和推力的不稳,降低飞机的安全性和可靠性。Nastrom 等[11]开发的基于Kolmogorov 频谱模型很难在时域建立模型。冯卡尔曼[12]模型可以近似Kolmogorov 频谱模型,但由于模型分数阶次高导致在时域中也存在问题。Kopasakis等[13]总结前人经验,以典型的大气扰动的代表性分数阶形式开发出更准确的模型,通过传递函数和扰动频率研究具有代表性的大气湍流时域模型。大气湍流干扰原理如图5所示。
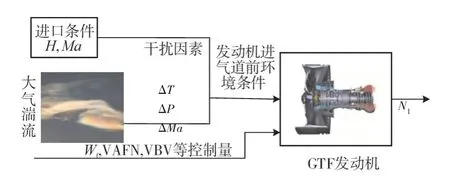
图5 大气湍流干扰原理
本文应用Kopasakis大气湍流模型计算大气扰动导致的声速、温度、压力的变化。以单位幅度正弦曲线的组合的形式来模拟时域下的大气干扰模型输入。实际数学模型如图6所示。
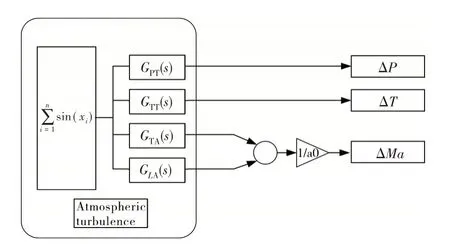
图6 大气湍流模型数学模型
图中:Ma为马赫数;a0为当地声速,m/s。
Kolmogorov 频谱表示1 个随机的大气湍流场谱密度

式中:St(k)为干扰形;αt对于每种干扰为常值;ε为涡流耗散速率,m2/s3;k为波数,cycles/m。
传递GLA、GTA、GTT、GPT可由式(22)推导出,GLA、GTA的单位是m/s,GTT的单位是K,GPT的单位是Pa。
1.6 功率提取干扰模型
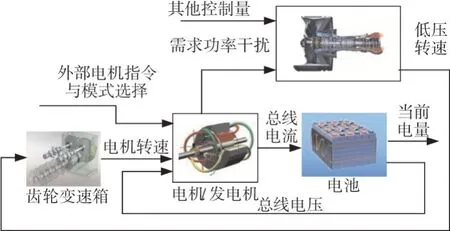
图7 GTF发动机中功率提取干扰原理
随着模式的切换,控制器会根据当前电池容量给出合理的电机指令,同时由于整个功率提取的系统的运作,发电机会从发动机中提取相应的需求功率ΔPm,这就导致了飞机在飞行过程中不可避免地被干扰。功率提取时低压轴平衡方程为

2 线性自抗扰控制设计
LADRC 控制器由ADRC 控制器简化而来,是将跟踪微分环节(Tracking Differentiation,TD)省略,将ESO(Extended State Observer)中的非线性函数部分改为线性LSEO,非线性PD 改为线性PD。采用LADRC技术不仅能保证在达到控制精度和速度要求的同时,降低调参难度,还能实时估计系统不确定扰动总和,消除扰动对输出的影响[16-17]。LADRC 的结构如图8所示。图中:B为PD 环节的控制参数;r为转速指令信号;y为低压轴转速;d为干扰信号,不需要知道其具体表达形式;u为控制量即燃油。
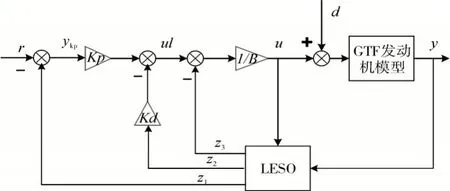
图8 线性自抗扰控制原理
GTF发动机是2阶系统
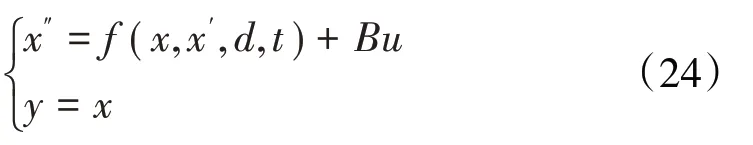
式中:x,x′,x″,y分别为系统状态量,即转速与其1、2 阶导数。
LESO的原理为
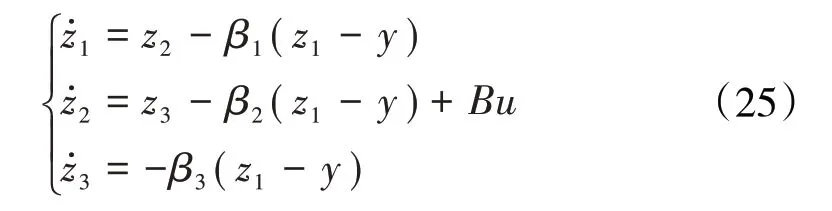
式中:β1、β2、β3为LESO 中的可调参数;z1、z2、z3分别为输出信号y、y的微分及扩张状态对系统未知干扰的估计。
LESO 估计整个系统总的未知因素,将这些作为总干扰准确地观测出来并引入控制回路中补偿,从而达到抗干扰的目的[18]。
PD环节
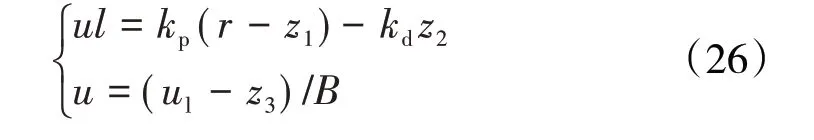
式中:kp、kd、B为PD 环节的控制参数,其作用是对扰动补偿后的系统进行校正,使其满足系统各项指标的要求。
根据参数配置方法[9,15],可以较为方便地选取上述6个可调参数。参数选取规则为
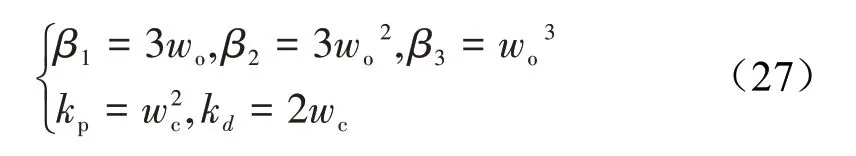
式中:wo、wc分别为观测器带宽和控制器带宽。
3 模型与控制的HIL平台集成与验证
3.1 HIL平台介绍
在当代对航空发动机控制研究中,硬件在回路平台的作用日益明显,平台功能包括发动机控制系统的验证、发动机模型深入研究与改进、先进控制算法的优化、飞机各种飞行条件以及故障等状态的模拟。仿真平台如图9所示。

图9 航空发动机控制系统硬件在环集成验证平台
平台有3 大模块。监控工作台:主要由主控计算机和综合测控计算机组成,其功能是平台监控、操作管理、故障注入等。仿真器:主要由发动机模型机、执行机构模型机、PXI 工控机、状态操纵装置、信号调理装置、负载模拟装置、适配装置等组成,主要模拟飞机在整个包线内。控制器:由EEC 以及EEC 上位机组成,功能是控制发动机状态。
3.2 仿真结果分析
3.2.1 模型一致性对比
数字仿真与HIL仿真对比如图10、11所示。PLA指令在90%、80%、70%之间不断阶跃。结果表明,在稳态时,PID 控制的转速的相对误差最大不超过0.18%,LADRC 控制的转速的相对误差最大不超过0.05%;在PLA 指令阶跃时,出现最大误差,PID 控制器是1.3%,而LADRC 控制器是0.6%。另外,从图11中可见,稳态时LADRC 控制下的转速抖动明显小于PID控制器的,说明LADRC 本身对于抑制HIL平台中各种硬件环节等不确定干扰有很好作用。
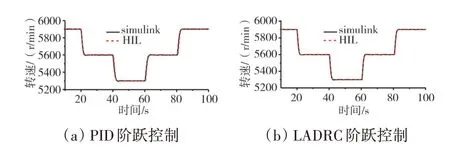
图10 闭环动态过程仿真曲线
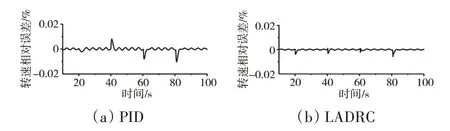
图11 转速相对误差
3.2.2 LADRC与PID控制在2类平台中的对比
大气湍流模型在不同时间段内给发动机模型带来不同的扰动输入,如图12 所示。从图12(a)中可见,在第40~50 s 给入静压扰动,压力变化为±10 kPa;从图12(b)中可见,在第60~80 s给入静温扰动,温度变化为±20 K;从图12(c)中可见,在第120~130 s给入马赫数扰动,马赫数变化为±0.05;在第180~190 s将上述各类大气干扰同时加入;从图12(d)中可见,在第150 s让发动机加载功率提取模型,在第160 s卸载功率提取模型,在这10 s 内约为310 kW(负号表示从发动机抽取功率)。功率提取主要发生在高空巡航状态下,所以此干扰只在高空状态下进行仿真。
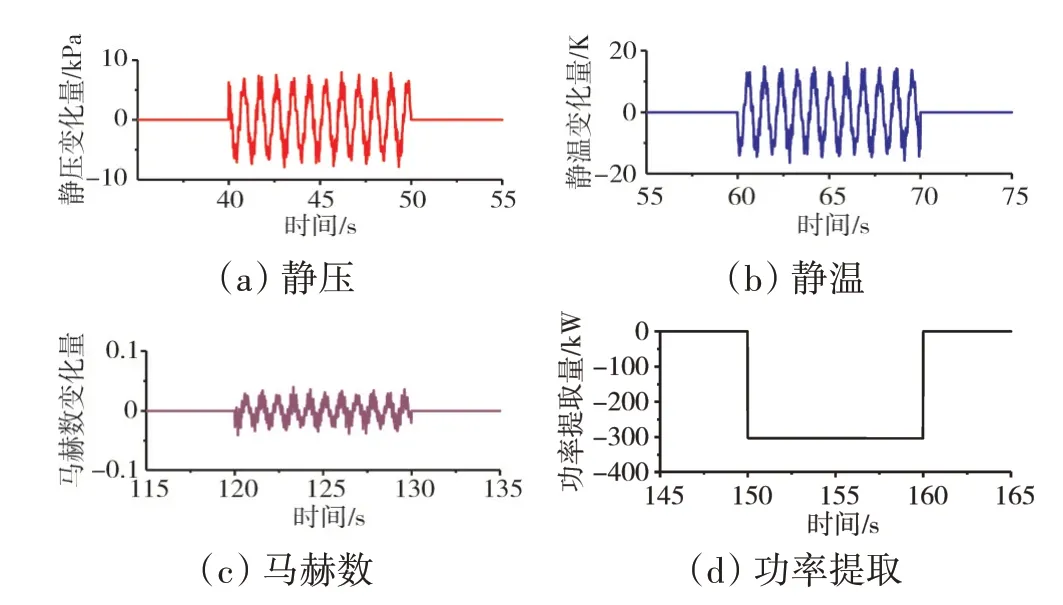
图12 各类干扰信号曲线
在地面点验证大气干扰3 个影响因素在LADRC与PID 控制中的效果。在Simulink 平台中的运行结果如图13(a)、(c)、(e)、(g)所示,在HIL 中的运行结果如图(b)、(d)、(f)、(h)所示。在这2 个平台,LADRC的转速抖动程度都要小于PID控制的。
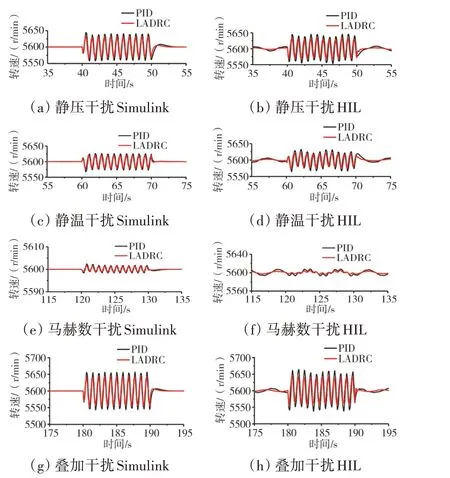
图13 H=0 m、Ma=0时的干扰响应
模型运行在高空巡航条件(H=10668 m,Ma=0.8)下模拟功率提取干扰如图14 所示。从图中可见,在巡航条件下发动机可以稳定向电力部件传递功率给电池充电,在高空巡航时同类型干扰对于发动机转速的影响比地面状态影响稍大,并且LADRC 控制器在每个平台都展现了优越的抗干扰性能。
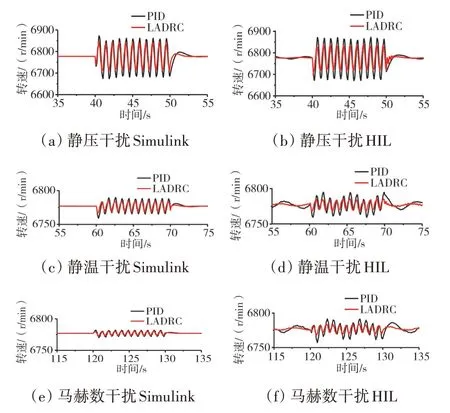
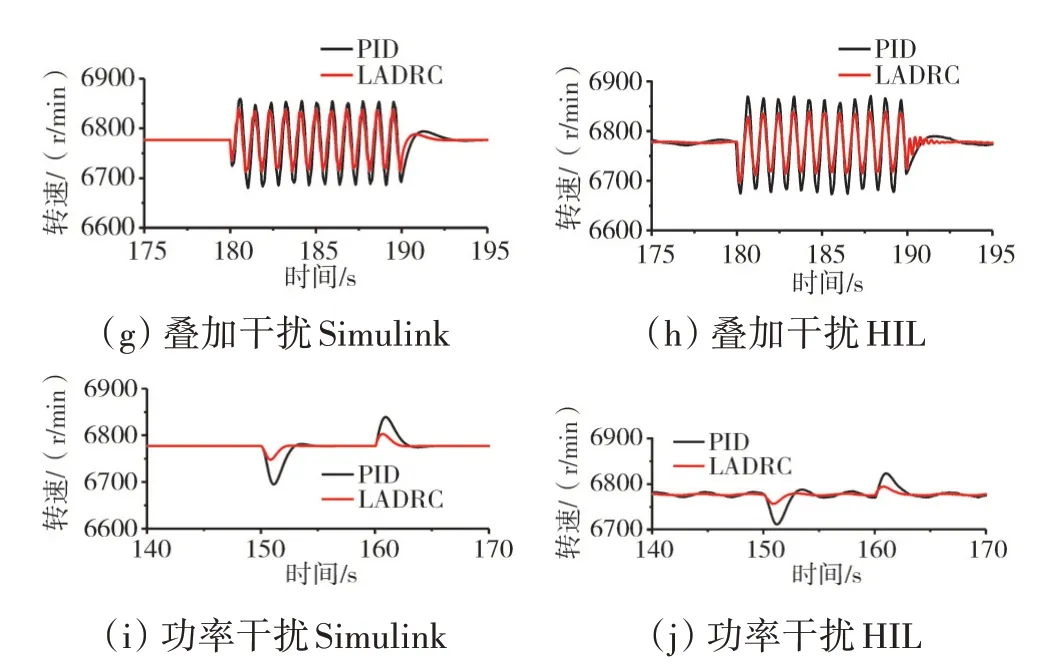
图14 H=10668 m、Ma=0.8时的干扰响应
为从数值上观察LADRC 控制比PID 控制对干扰的抑制效果,定义抗扰性能指标J,其意义是经过归一化,在一定时间内低压转速偏离期望转速的值的累计
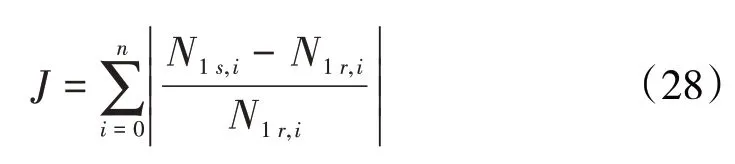
式中:N1s,i为i时刻实际低压转速;N1r,i为i时刻期望转速。
J越小意味着控制器的抗扰性能越好。抗扰性能J的结果见表3、4。
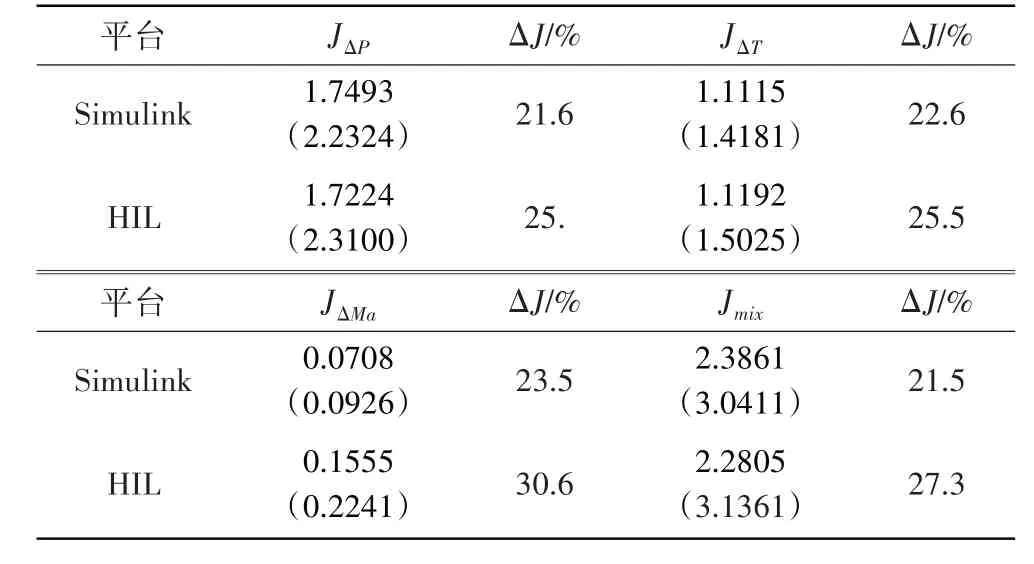
表3 地面(H=0 m、Ma=0)干扰测试对比
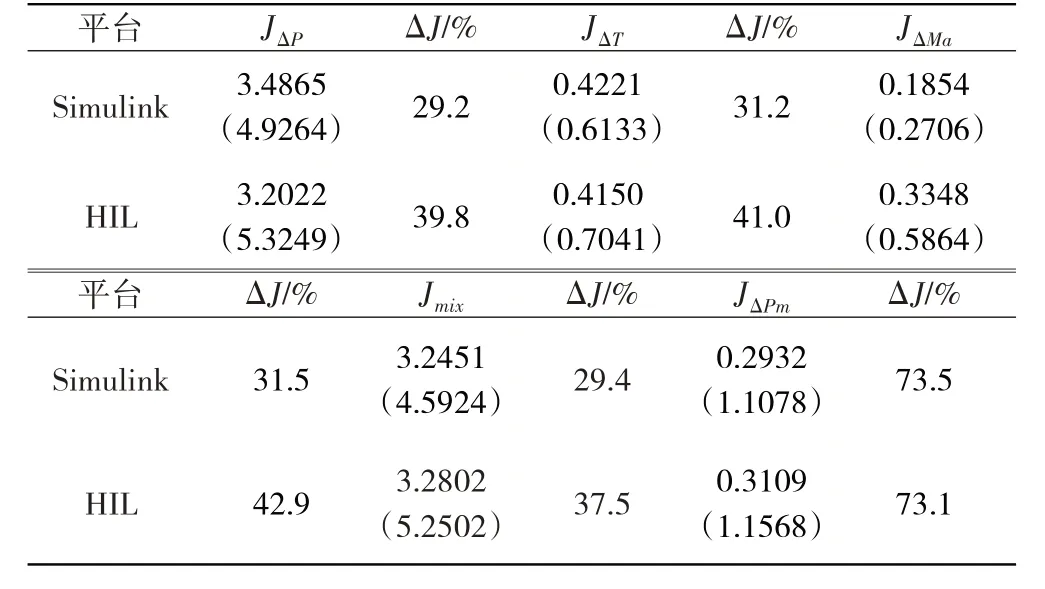
表4 高空巡航(H=10668 m、Ma=0.8)干扰测试对比
4 结论
(1)在闭环数字仿真与HIL 仿真中,无论是PID控制还是LADRC 控制,最大相对误差都在2%以内,满足模型的精确性要求;
(2)在2 个平台中,LADRC 控制对干扰的抑制效果普遍好于PID 控制,从性能指标J来看,LADRC 控制的抗扰性能比PID控制的至少提高20%以上;
(3)在2类平台中,HIL平台更接近于真实的发动机运行情况,由于硬件传递环节的噪声、电压波动、信号调理及传输延迟等不确定的因素,导致控制效果不如全数字仿真,但可以看到对于同类型干扰ΔJ%这个表示抗扰性能提升的参数,在HIL平台中的数据都大于Simulink 平台中的,说明LADRC 对于HIL 平台中各种真实存在且无法确定与建模的干扰有着比PID更好的抑制作用;
从上述结论中可见,LADRC 在航空发动机运行中抗各类干扰的有效性高。LADRC 不仅结构简单,易于调参,且能保持较好抗扰性能,保证了系统的安全工作。

