高低压转子弹性支承振动应力信号的LMD切片谱分析与时频分布
边 杰,陈亚农,卢艳辉
(1.中国航发湖南动力机械研究所,2.航空发动机振动技术重点实验室:湖南株洲 412002)
0 引言
航空发动机振动问题与转子密切相关,转子是发动机振动的主要激励源,转子的振动状态决定着航空发动机的运行状态。因此,对航空发动机转子进行振动监测,对监测信号进行频谱分析来获取转子的频谱特征是判别航空发动机运行状态的重要手段。
航空发动机转子碰摩故障是航空发动机的典型故障之一。对于双转子结构,高、低压转子的碰摩故障可通过是否出现组合频率来判断[1]。近年来,国内外学者对旋转机械转、静子碰摩问题进行了大量研究。林学森等[2]研究发现当发生转、静子碰摩时,机匣响应频谱中出现转子高倍频及其组合频率成分,高倍频成分幅值随碰摩程度加重而增大;周海伦等[3]以双转子航空发动机为研究对象,建立了双转子-滚动轴承-机匣耦合动力学模型,依据其计算分析得到双转子2 个激励频率的倍频、组合频率及其分频,可以作为航空发动机碰摩故障诊断的特征频率;陈果[4]针对航空发动机整机振动,建立了航空发动机转子-滚动轴承-机匣耦合动力学模型,其计算仿真表明:在临界转速以下,碰摩故障将产生较大的高次谐波,其中2 倍频较大,在临界转速以后,碰摩故障将产生较大的分数次谐波;晏砺堂等[5]通过理论分析、模型试验和实测结果分析发现,双转子发动机发生转、静子碰摩时,除了出现转子的基频振动外,还会出现多种倍频和分频振动以及2 转子转速频率的多种复合频率的振动;秦海勤等[6]发现在航空发动机双转子发生局部碰摩故障时,转子和机匣测点的频谱图中会出现转子的倍频和组合频率;梁智超等[7]在叶片和机匣发生轻微碰摩和严重碰摩时对转子和机匣的振动响应进行了试验测量,并使用时-频分析方法对振动信号进行了特征提取;王海飞等[8]提出了考虑多叶片-机匣耦合振动下的转、静子碰摩故障模型,通过仿真和试验验证了所提出的碰摩模型的正确性和有效性;李炳强等[9]基于弹性协调相容条件给出了新的叶片与机匣碰摩力模型,将文献结果与试验结果进行了对比,验证了碰摩模型的准确性;陈果等[10]进行了转子叶片-机匣的碰摩试验,采用频谱分析方法研究了机匣振动加速度信号的碰摩特征;太兴宇等[11]推导了叶片与机匣间的碰摩表征模型,并基于该模型分析了不同工况下叶片-机匣的耦合振动;马辉等[12]根据叶尖各节点径向位移与间隙之间的位置关系,对不同转速下叶片-机匣的碰摩过程进行数值仿真;张俊红等[13]通过碰摩试验获取了一定转速下叶片-机匣碰摩时的碰摩力和机匣上的加速度,并进行了对比分析;金业壮等[14]对航空发动机双转子系统的碰摩故障进行了动力学仿真研究,获得了轻微碰摩、较重碰摩和严重碰摩3 种状态下转子系统的时、频域振动响应;Prosvirin等[15]提出了诊断由轴不平衡和不同程度叶片碰摩引起的复合故障的方法,试验结果表明所提出的故障诊断模型对于不同的训练-测试数据均具有较好的收敛性;Chandra 等[16]利用转子启动时的振动数据,使用时频分析技术来解决转子故障识别问题。比较了短时傅里叶变换、连续小波变换和Hilbert-Huang变换3种信号处理工具的检测性能。以上针对转子碰摩故障诊断研究,多是基于实验室的模拟转子,对于实际航空发动机转子的碰摩故障诊断研究,特别是基于弹性支承振动应力信号的高、低压转子间的碰摩故障诊断研究甚少;而且,不同类型和结构的航空发动机转子间的碰摩故障特征本身存在差异。此外,以上研究多采用传统频谱分析方法,对于具有明显非平稳性的转子碰摩振动信号的故障特征提取存在其自身局限性。
鉴于此,本文采用局部均值分解[17](Local Mean Decomposition,LMD)方法对航空发动机高、低压转子弹性支承振动应力信号进行自适应分解,对分解结果进行切片谱分析和时频特征提取,并验证了所提出方法的有效性。
1 振动信号处理方法
LMD方法能自适应地将1个多分量信号分解成1组F(Production Function)分量之和。对于任意信号x(t),LMD的分解过程如下。
找出信号x(t)的所有局部极值点ni,然后分别计算均值mi和包络估计ai
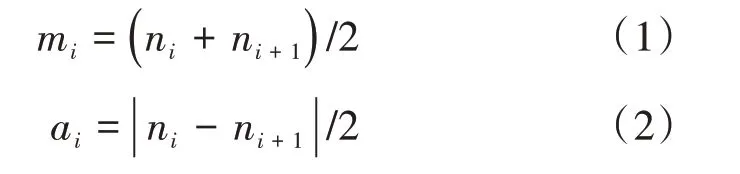
(1)使用滑移平均方法对局部均值和局部包络估计分别进行平滑处理,得到均值函数m11(t)和局部包络函数a11(t)。
(2)计算频率调制信号s11(t)。
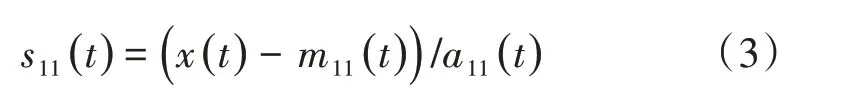
如果s11(t)不是1 个纯频率调制信号,将其作为新的原始信号,重复(1)~(3)步骤直到s1n(t),此时有包络函数
(3)将所有循环过程得到的包络估计相乘,得到瞬时幅值a1(t)。
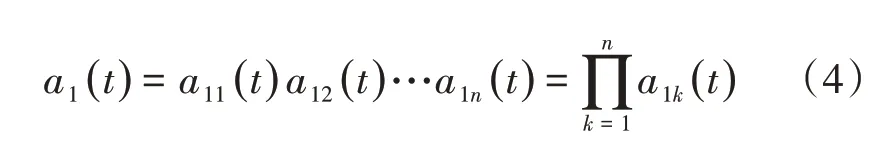
(4)可以由瞬时幅值a1(t)和纯频率调制信号s1n(t)相乘得到第1个F分量。
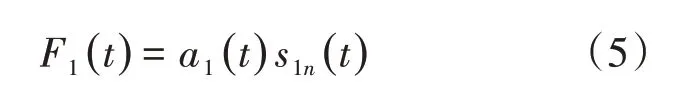
则第1 个F分量的瞬时频率f1(t)可从纯调频信号s1n(t)中得到,即
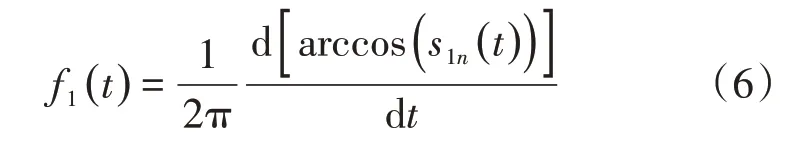
(5)从信号x(t)中分离出F1分量得到1 个新的信号。重复整个过程直到uk(t)为常数或者单调函数。至此,原始信号x(t)被重构为
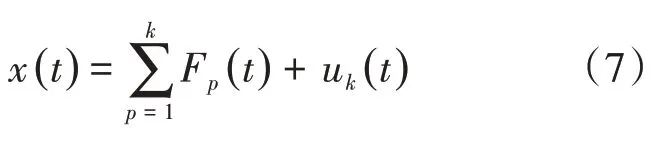
F分量切片谱定义为F分量F(t)的3阶累积量对角切片的傅里叶变换。不仅保留了3 阶累积量抑制高斯噪声的优点,同时简化了其计算过程。对于F分量F(t),其3阶累积量为c3a(τ1,τ2),对角切片为c3a(τ,τ)(τ1=τ2=τ)。定义F分量切片谱C(ω)[18]
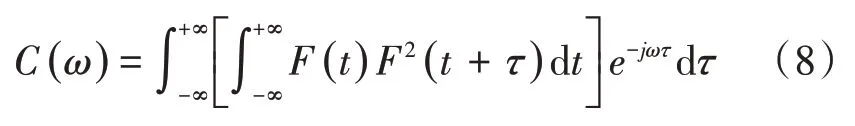
由LMD 分解得到各F分量的瞬时幅值ap(t)和瞬时频率fp(t),从而得到信号x(t)的时频曲线图,可以更好地表征信号x(t)的非平稳时变特征。
2 高、低压转子结构
某航空发动机是一种双转子结构发动机,其低、高压转子结构分别如图1、2 所示。低压转子采用0-2-1 的支承方式,其中,1 号轴承为滚珠轴承,带鼠笼弹性支承挤压油膜阻尼器,2 号和5 号轴承为滚棒轴承,且5 号轴承处有鼠笼弹性支承挤压油膜阻尼器;高压转子采用1-1-0 的支承方式,其中3 号轴承为滚珠轴承,4 号轴承为滚棒轴承,均带鼠笼弹性支承挤压油膜阻尼器。
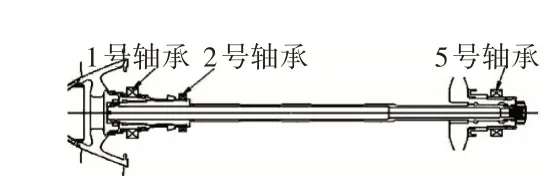
图1 低压转子结构
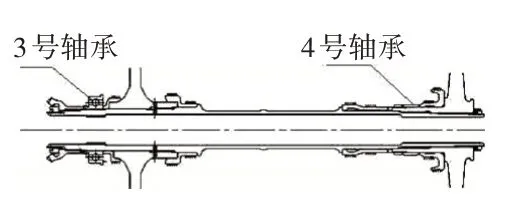
图2 高压转子结构
3 高、低压转子弹性支承振动应力信号分析
分别在低压转子的1号轴承和高压转子的3号轴承处的鼠笼弹性支承的弹条上粘贴应变片,用于监测某发动机试车过程中高、低压转子的振动情况。采用LMD 方法对所监测的弹性支承振动应力信号进行切片谱分析和时频特征提取,以辨别某发动机试车过程中高、低压转子振动信号中的频谱特征与谱线来源,为发动机高、低压转子的运行状态判别提供依据。试验中,采样频率为6000 Hz,所分析的弹性支承应力信号时长均为1 s。
3.1 发动机振动正常状态
在发动机振动正常状态下,所采集的低压转子弹性支承振动应力信号及频谱如图3(a)所示。从图中可见,在2400 Hz附近有较大峰值,在低压转子基频fL处的峰值相对较小。采用LMD 方法对低压转子弹性支承应力信号进行自适应分解,得到4 个模态分量,如图3(b)所示。由于F1分量和F2分量的峰值频率在1000 Hz 以上,而本文对应故障特征的频率主要集中在1000 Hz 以下。进一步对1000 Hz 以下的F3分量和F4分量进行切片谱分析和时频分析,结果如图3(c)、(d)所示。从图3(c)中可见,F3分量和F4分量只存在低压转子的基频fL/2、2 倍频2fL及分频fL/2 和fL/4 成分;从图3(d)中可见,低压转子的弹性支承振动应力信号所包含的1000 Hz 以下的2 个F分量的瞬时频率和瞬时幅值均随时间不断变化,表现出强的非线性和非平稳性。
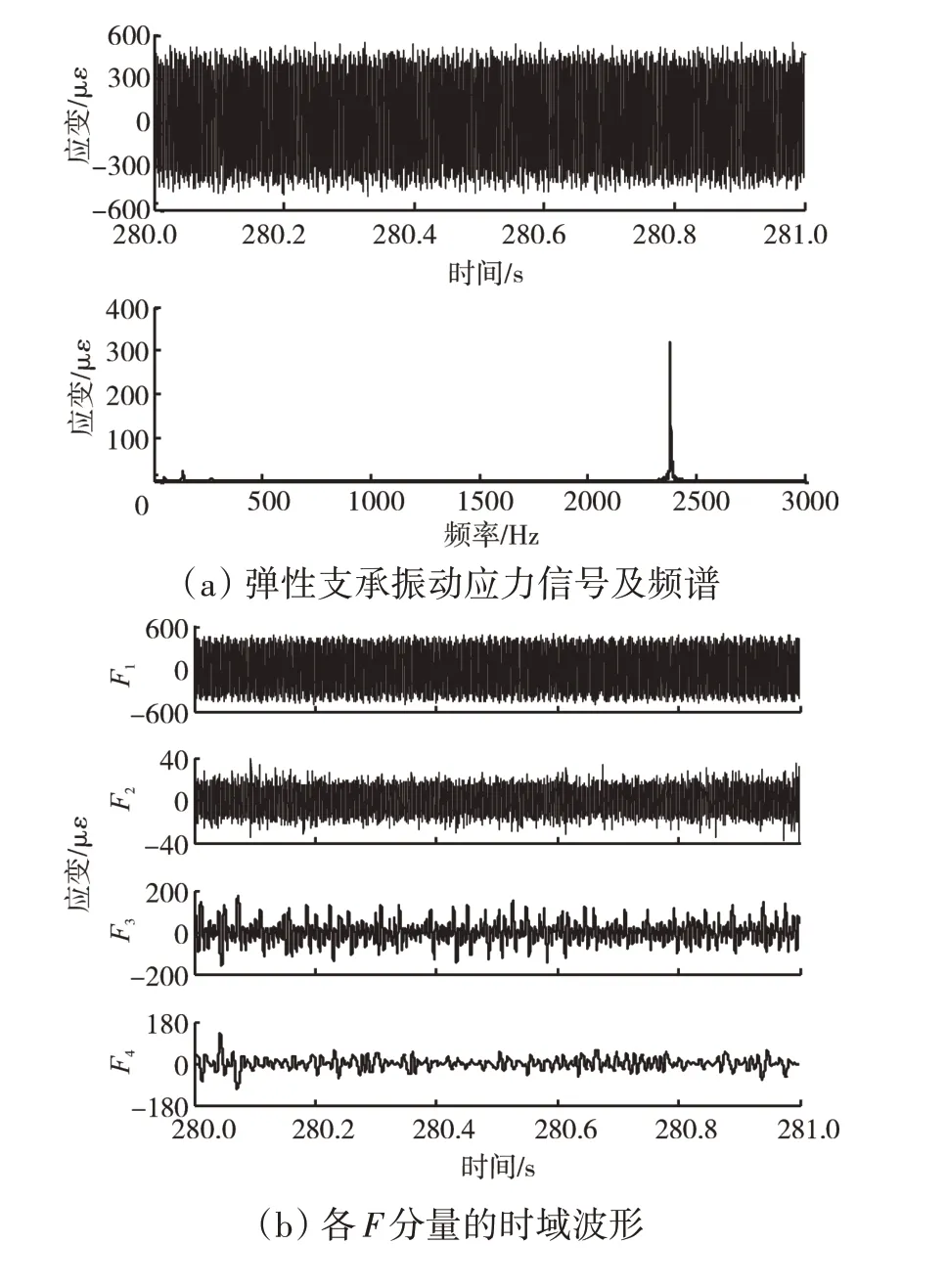
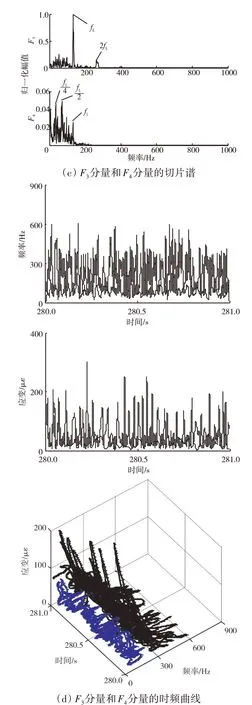
图3 振动正常状态下低压转子弹性支承振动应力信号
发动机振动正常状态下高压转子的弹性支承振动应力信号及频谱如图4(a)所示。同样,在2400 Hz附近有较大峰值,在高压转子基频fH处的峰值相对较小。采用LMD 方法将其分解成3 个模态分量,如图4(b)所示。对1000 Hz 以下的后2 个模态分量进行切片谱分析与时频分析,结果如图4(c)、(d)所示。图4(c)的切片谱中F2分量中只存在高压转子的基频fH与2倍频2fH成分。图4(d)中F2分量和F3分量的瞬时频率和瞬时幅值也同样表现出强的时变特征,围绕其各自的峰值频率上下波动。
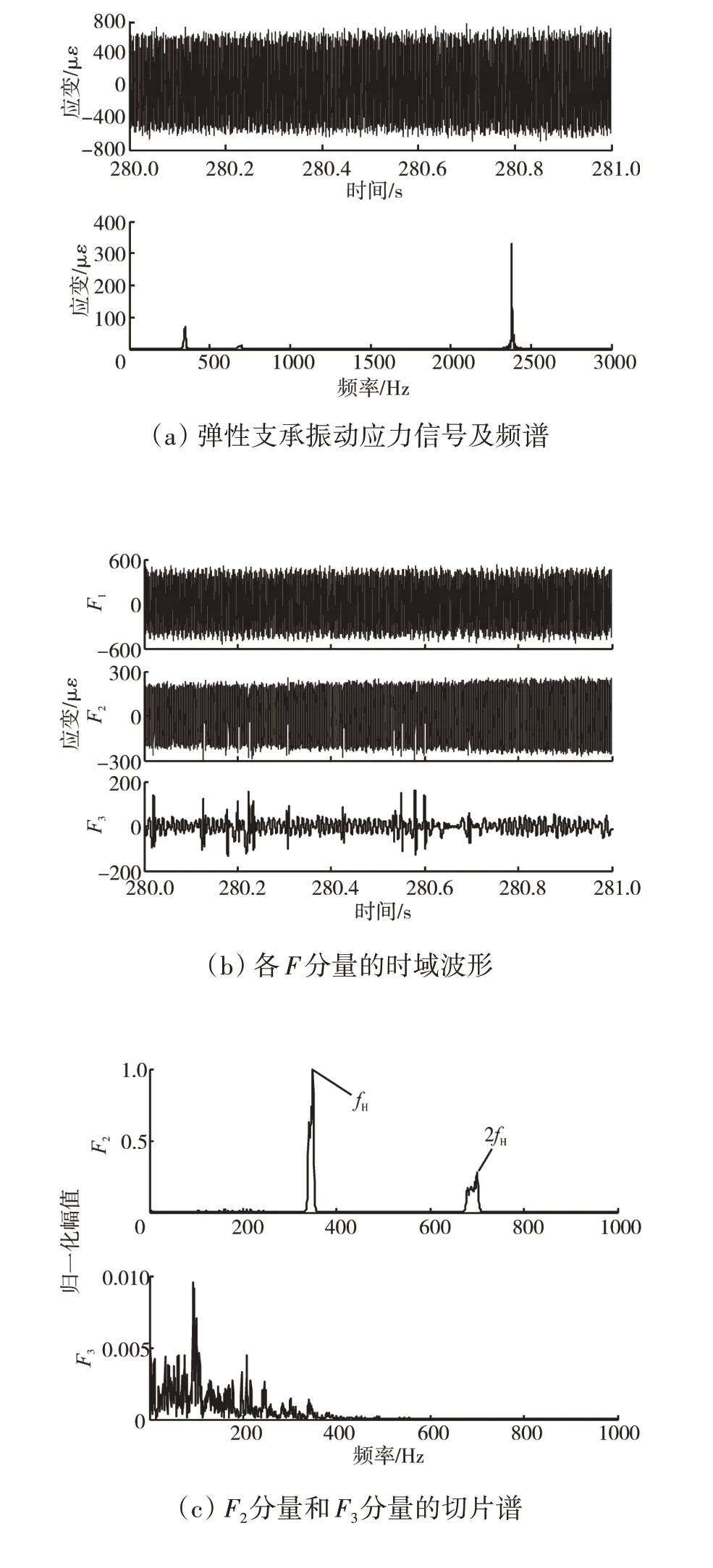
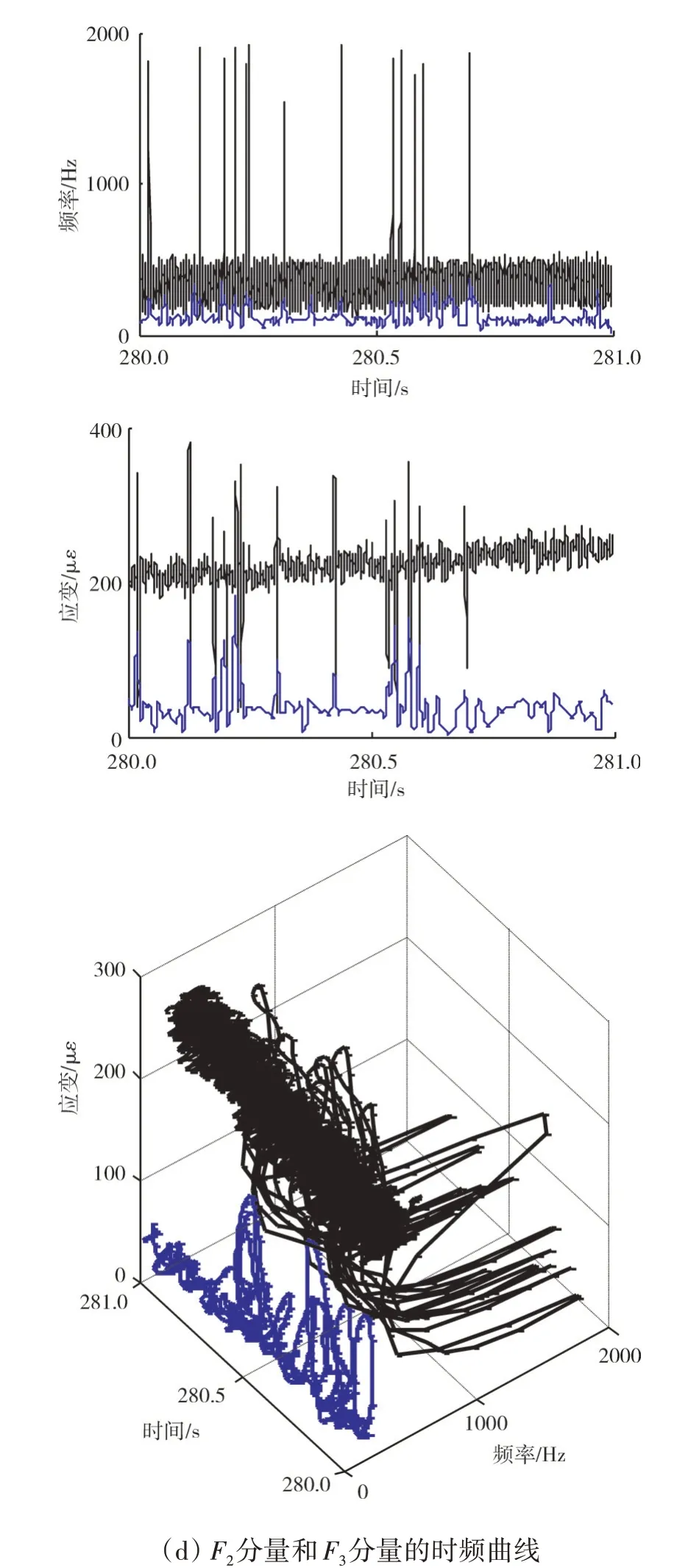
图4 振动正常状态下高压转子弹性支承振动应力信号
3.2 发动机振动异常状态
发动机振动异常时,采集的低压转子弹性支承振动应力信号及频谱如图5(a)所示。从图中可见,与图3(a)发动机正常状态时相比,发动机振动异常时,低压转子在2400 Hz 附近的峰值频率依然存在,同时在低压转子基频fL附近出现了一些幅值较小的峰值频率。采用LMD 方法对其进行自适应分解得到4 个F分量,如图5(b)所示。同样对1000 Hz 以下的后2个F分量进行切片谱分析和时频分析。与图3(c)中发动机振动正常状态时的切片谱相比,图5(c)中发动机振动异常状态时F3分量和F4分量的切片谱除了存在低压转子的基频fL及2倍频分量2fL,还存在高压转子的基频分量fH、低压转子基频及2 倍频对高压转子基频的调制频率fH-fL和fH-2fL、高压转子基频对低压转子3 倍频的调制频率3fL-fH。这些调制频率的存在,说明高压转子和低压转子之间发生了耦合振动,其频谱符合高、低压转子的碰摩故障特征。相比于图3(d)发动机正常状态时,图5(d)中F3分量和F4分量的瞬时频率和瞬时幅值则表现出更强的非线性和非平稳特征。
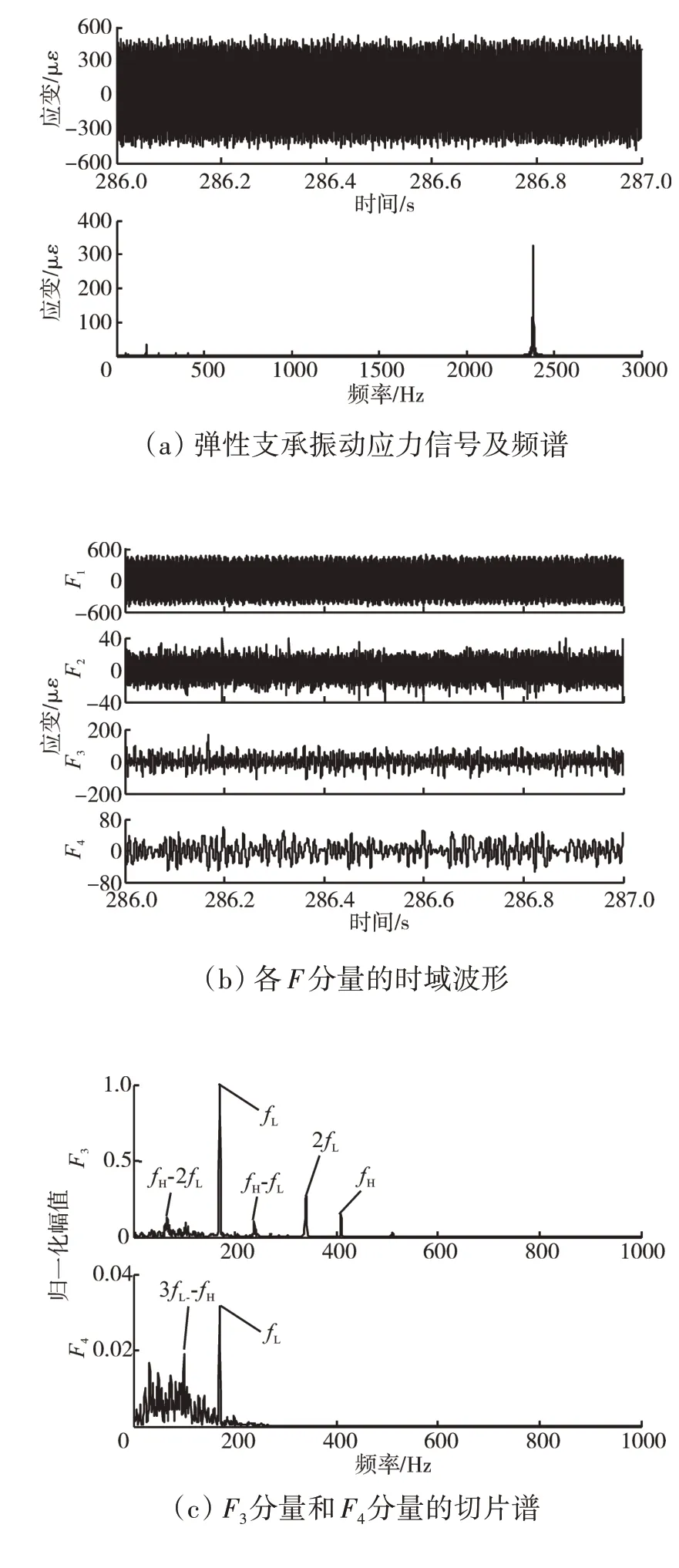
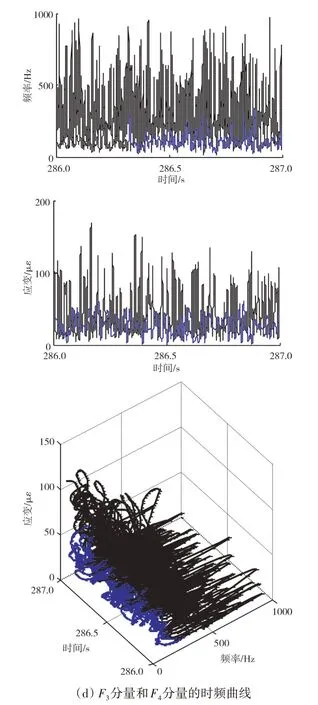
图5 振动异常状态下低压转子弹性支承振动应力信号
发动机振动异常时,采集的高压转子弹性支承振动应力信号及频谱如图6(a)所示。从图中可见,发动机振动异常时,高压转子在2400 Hz 附近以及高压转子基频fH处均有较大峰值。采用LMD 方法分解得到的发动机振动异常时高压转子弹性支承振动应力信号的3 个F分量,如图6(b)所示。其中所关心的1000 Hz 以下的2 个F分量的切片谱如图6(c)所示。从图中可见,F2分量和F3分量的切片谱除了存在高压转子的基频fH与2 倍频2fH成分,还存在低压转子基频fL与高压转子基频对低压转子3 倍频的调制频率3fL-fH成分,符合高、低压转子碰摩后的耦合振动特征。F2分量和F3分量的瞬时频率和瞬时幅值曲线如图6(d)所示。从图中可见,2个F分量均表现出时变的瞬时特征,且F3分量的时变特征更加明显。
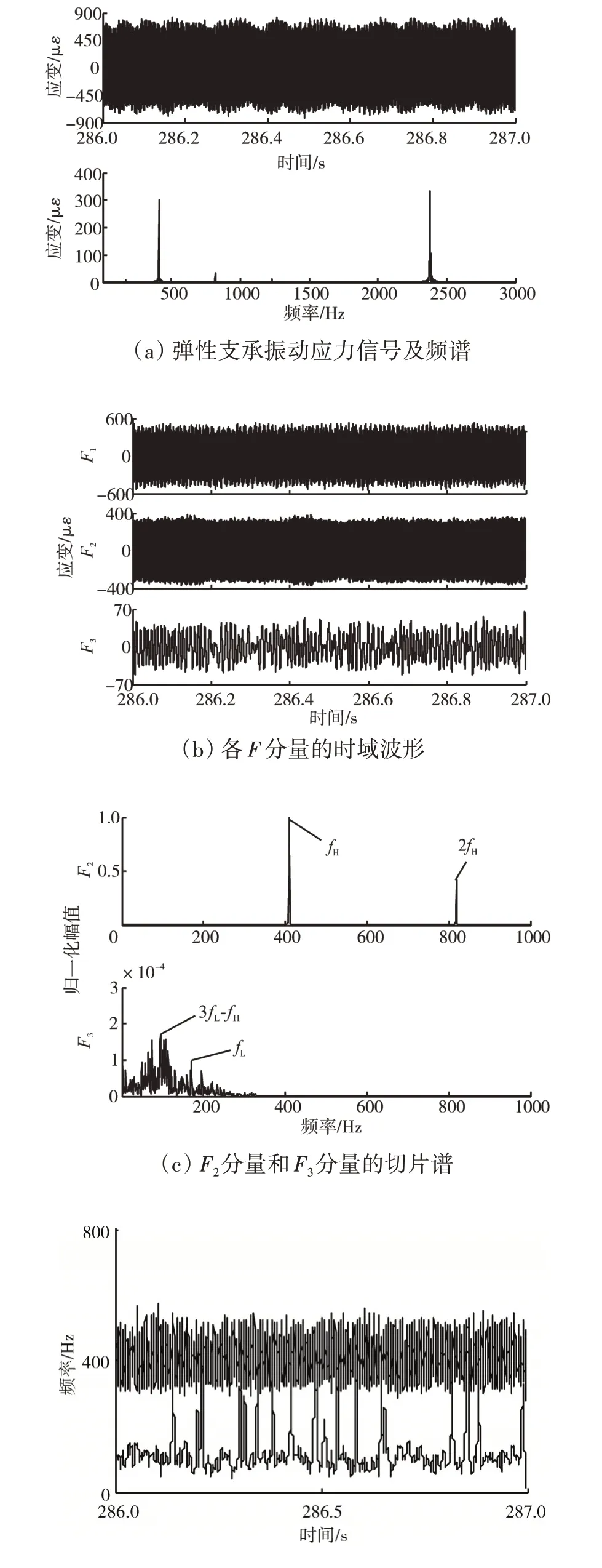
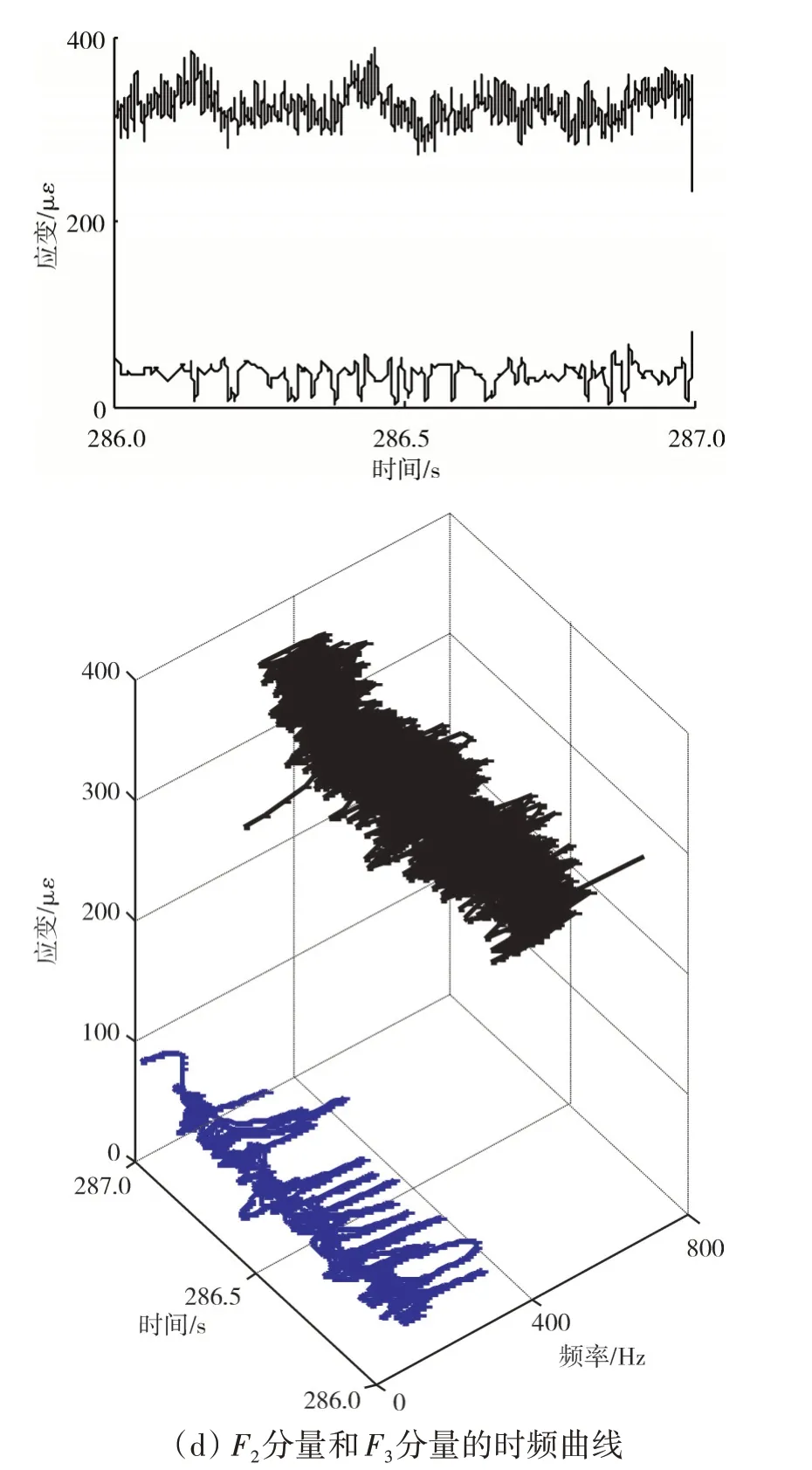
图6 振动异常状态下高压转子弹性支承振动应力信号
4 结论
(1)在发动机振动正常状态下,低压转子弹性支承振动应力信号的LMD切片谱中只存在低压转子的基频fL、2倍频2fL及分频fL/2和fL/4成分。同时其F分量的瞬时频率和瞬时幅值均随时间不断变化,表现出强的非线性和非平稳性。
(2)在发动机振动正常状态下,高压转子弹性支承振动应力信号的LMD切片谱中F2分量中只存在高压转子的基频fH与2 倍频2fH成分。其F分量的瞬时频率和瞬时幅值同样表现出强的时变特征,围绕其各自的峰值频率上下波动。
(3)在发动机振动异常状态下,低压转子弹性支承振动应力信号的LMD切片谱中除了存在低压转子的基频fL及2倍频分量2fL,还存在高压转子的基频分量fH、低压转子基频及2 倍频对高压转子基频的调制频率fH-fL和fH-2fL、高压转子基频对低压转子3倍频的调制频率3fL-fH。同时其F分量的瞬时频率和瞬时幅值则表现出更强的非线性和非平稳特征。
(4)在发动机振动异常状态下,高压转子弹性支承振动应力信号的LMD切片谱中除了存在高压转子的基频fH与2倍频2fH成分,还存在低压转子基频fL与高压转子基频对低压转子3 倍频的调制频率3fL-fH成分。其F分量均表现出时变的瞬时特征,且F3分量的时变特征更加明显。

