运用数学计数原理速解同分异构体数目判断题
鲁名峰

摘要:分析阐释分类加法计数原理和分步乘法计数原理,举例详解运用两个数学原理推理限定条件有机物同分异构体数目的方法。该方法简单易学、快捷高效,既能防止重复书写,又能避免遗漏,实践效果显著。
关键词:同分异构体; 分类加法计数原理; 分步乘法计数原理; 同分异构体数目判断
文章编号:10056629(2021)11008405
中图分类号:G633.8
文献标识码:B
同分异构体是高考热门考点。笔者统计近五年(2016~2020年)高考全国卷15套试卷中的有机化学试题获知: 有机单选题中同分异构体出现6次,频率达40%,位居高频考点序列第四;有机非选择题中同分异构体考点出现14次,频率达93%,位居高频考点序列第二。
同分异构体考点的能力要求为: 准确理解键线式表达的有机物分子的空间结构,熟练掌握有机物分类系列,严密有序地推断同分异构体数目,快速书写限定条件的同分异构体。这些应试要求对学生思维的准确性、条理性、发散性、全面性、敏捷性均提出了较高要求。同分异构体考点既能考查考生的化学学科必备知识,又能检测考生的化学学科关键能力。
高考化学答题时间分配一般是: 单项选择题每道1分钟,非选择大题每道8分钟,平均到每一空约1.5分钟,还留出10分钟的机动时间。如果在限定时间内做不出来,就意味着考生无法做完全部试卷。如果考生在考场上采用列举法逐一写出同分异构体再统计数目,最少得5分钟以上,还要特别熟练才行,显然列举法不可取。运用数学计数原理可以快速解答同分异构体的数目判断问题。
1 分类加法计数原理
1.1 数学原理
完成一件事有两类不同方案(两类不同方案中的方法互不相同),在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法。那么完成这件事共有N=m+n种不同的方法。
1.2 推论
完成一项工程有n个方案,每个方案有mi种不同方法,所有方法互不相同,每种方法可以独立完成该项工程,则完成该项工程的方法共有: N=∑ni=1mi[1]。
举例: 假设张老师5月4日从深圳去北京,可以选择飞机、高铁、快车、自驾四种方式。其中飞机可以乘坐国航、南航、川航、深航各一航班,高铁该日有四列车次,快车有五列车次,自驾可以走三种不同高速线路,如图1所示。
举例图1
则张老师从深圳去北京的方法一共有: 4+4+5+3=16种。
1.3 迁移应用——同分异构体数目判断
首先根据化学式确定有机物分子的不饱和度,由不饱和度判断属类别,每个属类别再依次按碳链异构、位置异构推断同分异构体数目,把所有类别数目相加即得总的同分异构体数。
例1 分子式为C4H7Cl的同分异构体(不考虑立体异构和顺反异构)共有几种?
解析: 有机物C4H7Cl是C4H8的一氯代烃,C4H8的不饱和度是1,故该有机物为一氯代烯烃或一氯代单环烷烃两类。
(Ⅰ) 一氯代烯烃同分异构体:
碳链异构有两类: (1)C—C—C—C和(2)CCCC。
(1) 的双键位置异构有两种: CC—C—C, C—CC—C。氯原子连在不等效碳原子上,得不同种同分异构体:C①↓C②↓C③↓C④↓和⑤↑CC↑⑥CC,共4+2=6种。
(2) 的双键位置异构只有1种CCCC,氯原子连在不等效碳原子上,得不同种同分异构体:
C⑦↓CCC⑧↓,共2种。
(Ⅱ) 一氯代单环烷烃同分异构体:
碳链异构:和,氯原子连在不等效碳原子上,得不同种同分异构体:
和,共1+3=4种。
由分類加法计数原理得同分异构体总数为: 4+2+2+1+3=12种。
例2 [2019新课标Ⅱ, T13]分子式为C4H8BrCl的有机物共有(不含立体异构)( )。
A. 8种
B. 10种
C. 12种
D. 14种
解析: C4H8BrCl的不饱和度是0,是二卤代烷烃。
碳链异构有2种,每一种碳链用定氯移溴的方法得出同分异构体数,分别为:
ClC①↓C②↓C③↓C④↓,4种;C⑤↓CCl⑥↓C⑦↓C⑧↓,4种;
ClC⑨↓CC⑩↓CB11↓,3种;CB12↓CClCC,1种。
由分类加法计数原理得同分异构体总数为: 4+4+3+1=12种。
例3[2016新课标Ⅰ卷,T38(5)]具有一种官能团的二取代芳香化合物W是E(H3COOCCOOCH3)的同分异构体,0.5mol W与足量碳酸氢钠溶液反应生成44g CO2, W共有 种(不含立体结构),其中核磁共振氢谱为三组峰的结构简式为 。
解析:0.5mol W与足量碳酸氢钠溶液反应生成44g CO2,说明W分子中含有2个—COOH,则其可能的支链情况是: —COOH、 —CH2CH2COOH;—COOH、 —CH(CH3)COOH; 2个—CH2COOH; —CH3、 —CH(COOH)2四种情况。每一种情况有邻位、间位、对位三种同分异构体,故W可能的同分异构体种类共有4×3=12种,其中核磁共振氢谱为三组峰的结构简式为:HOOCCH2CH2COOH。
2 分步乘法计数原理
2.1 数学原理
完成一件事需要两个步骤(无论第1步采用哪种方法,都不影响第2步方法的选取),做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N=m×n种不同的方法。
2.2 推论
完成一件事,需要n個步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……做第n步有mn种不同的方法。那么完成这件事共有N=m1×m2×m3×…×mn种不同的方法[2]。
举例: 做一件事(从A到D)需2步完成: A→B→D, A→B有3种办法,B→D有2种办法,如图2所示。
举例图2
则做这件事一共有3×2=6种办法。
2.3 迁移应用——同分异构体数目判断
例4 有机物甲分子式为C12H16O2,在酸性条件下水解生成乙和丙。丙遇FeCl3溶液显紫色,核磁共振氢谱有四个峰且峰面积之比为1∶2∶2∶1,甲可能的结构有( )
A. 6种
B. 8种
C. 10种
D. 12种
解析: 丙遇FeCl3溶液显紫色,则丙有酚羟基。丙的核磁共振氢谱有四个峰且峰面积之比为1∶2∶2∶1,则丙只能是苯酚。即有机物甲为羧酸苯酚酯,其基本结构为:OCOC5H11。有机物甲的同分异构体数目由两个分子碎片的异构体决定: 酚类异构体数和戊烷基C5H11的异构体数决定。苯酚的酚类同分异构体只有1种,戊烷基异构体有8种,则甲的同分异构体数目可由分步乘法计数原理计算: 1×8=8种。
例5有机物甲分子式为C11H13O2Cl的芳香族化合物,在酸性水溶液中水解后生成乙和丙两种物质,丙能使FeCl3溶液显紫色,红外光谱显示丙中含有氯原子而无烃基取代基,则有机物甲可能的结构有几种?
解析: 有机物甲在酸性水溶液中水解生成乙和丙,丙遇FeCl3溶液显紫色,则丙有酚羟基。红外光谱显示丙中含有氯原子而无烃基取代基,则丙的苯环上只有羟基和氯原子。由此得出有机物甲为氯代苯酚与五碳饱和一元羧酸生成的酯。
氯代苯酚有邻、间、对位3种同分异构体,五碳饱和一元羧酸的同分异构体数目由丁烷基决定,丁烷基有4种同分异构体。由分步乘法计数原理得有机物甲的同分异构体数为: 3×4=12种。
例6 [2013年全国卷Ⅰ, T12]分子式为C5H10O2的有机物在酸性条件下可水解为酸和醇,若不考虑立体异构,这些酸和醇重新组合可形成的酯共有( )。
A. 15种
B. 28种
C. 32种
D. 40种
解析: 由题意知该有机物为酯,水解可能的酸和醇如表1所示。
酸的同分异构体数为1+1+1+2=5;醇的同分异构体数为4+2+1+1=8。根据分步乘法计数原理,由水解产生的酸和醇重新组合的酯共有: 5×8=40种[3]。
3 综合两个数学计数原理进行推断
例7 有机物甲分子式为C9H9O2Cl的芳香族化合物,能同时满足下列条件的同分异构体可能有几种?a.苯环上连接着Cl; b.在酸性水溶液中水解后的一种产物遇FeCl3溶液显紫色。
解析: 在酸性水溶液中能水解,说明有酯基。水解后一种产物遇FeCl3溶液显紫色,说明该水解产物中含有酚羟基。结合分子式可以推断有机物甲是氯代苯酚与羧酸生成的酯。
每类酯由氯代苯酚与羧酸酯化而成,由分步乘法计数原理得同分异构体数如表2所示。
每类都可以构成酯,共有4类,由分类加法计数原理得同分异构体共有: 3+10+10+16=39种。
4 熟记分子“构件”异构体数目
记住苯环上不同个数取代基的同分异构体数目和不同数目碳原子的烷基的同分异构体数目,运用上文讲的两种数学计数原理,可以快速推断同分异构体数目。
苯环连有不同数目和类别的取代基时的异构体数如表3所示。
不同碳原子数的烷基的同分异构体数如表4所示。
其中XYZW代表苯环上四种不同的取代基,比如苯环上有XYZW四种不同的取代基时有30种同分异构体。这些同分异构体数目是通过列举法逐一写出同分异构体后统计得出或通过排列组合数学推理得出的,因篇幅所限本文不再赘述,考生没有必要也没有时间在考场上逐一书写或推理,熟记这两个表格中的内容即可快速推理[4, 5]。
例8 [2013新课标Ⅰ卷,T38(6)]F(C8H8O2)的同分异构体中,既能发生银镜反应,又能与FeCl3溶液发生显色反应的共有 种,其中核磁共振氢谱为5组峰,且峰面积比为2∶2∶2∶1∶1的为 (写结构简式)。
解析: 能发生银镜反应说明有醛基,又能与FeCl3溶液发生显色反应说明有酚羟基,故F有两类不同类型的取代基,如表5所示。
同分异构体有13种,其中峰面积之比为2∶2∶2∶1∶1的结构简式为:HOCH2CHO。
例9 [2014全国Ⅰ卷,T38]F(C8H11N)的同分异构体中含有苯环的有 种(不考虑立体异构)。其中核磁共振氢谱中有4组峰,且面积比为6∶2∶2∶1的是 (写出其中的一种结构简式)。
解析: 含苯环,抠除一个ph—,剩—C2H6N,则F为胺,有下列8种情况,见表6。
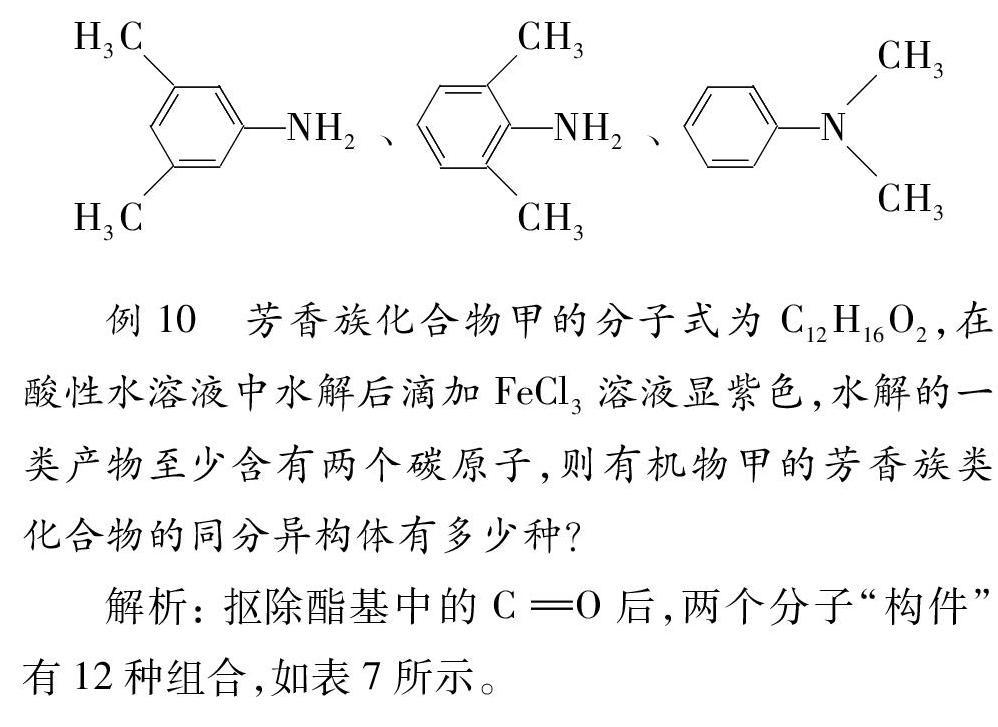
含有苯环的同分异构体有19种,其中核磁共振氢谱中有4组峰,且面积比为6∶2∶2∶1的有下列三种,任写一种即可:
H3CNH2H3C、CH3NH2CH3、NCH3CH3
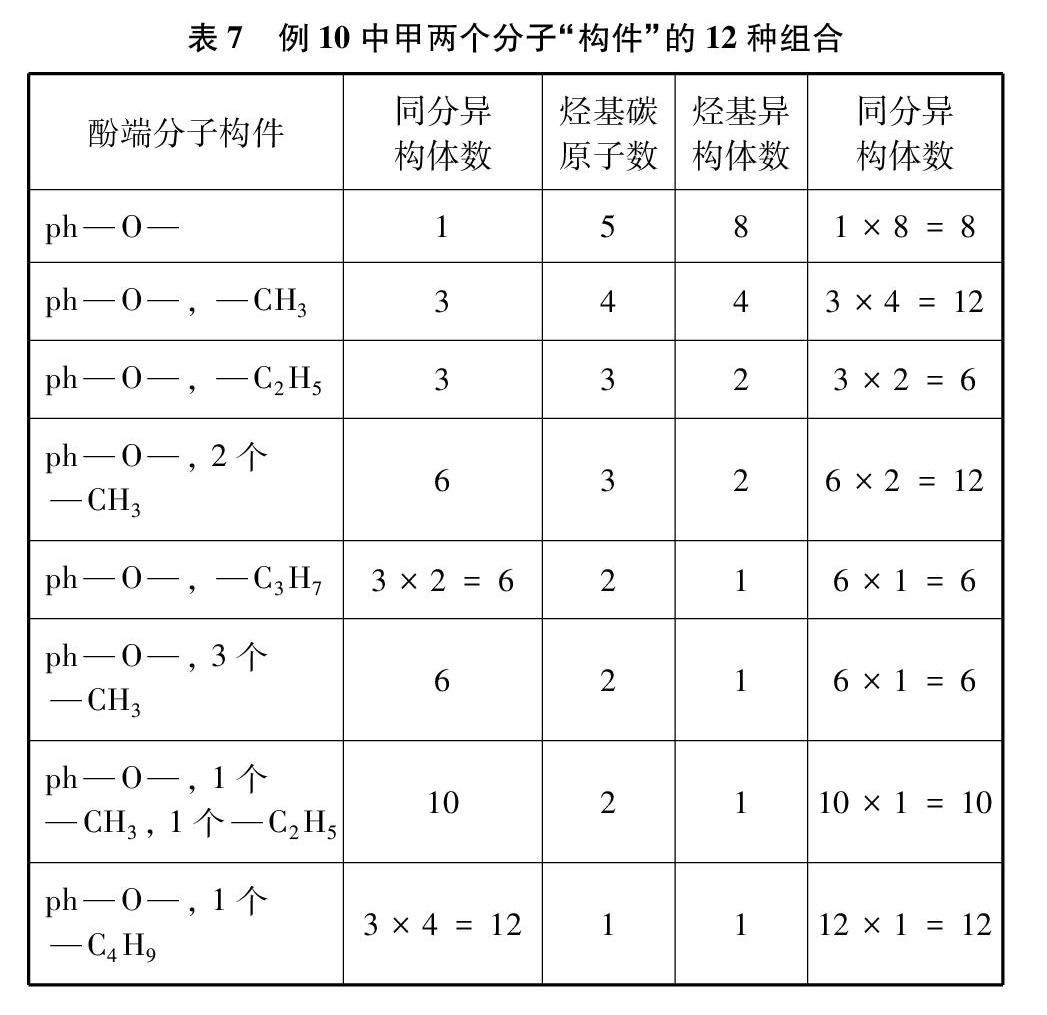
例10 芳香族化合物甲的分子式为C12H16O2,在酸性水溶液中水解后滴加FeCl3溶液显紫色,水解的一类产物至少含有两个碳原子,则有机物甲的芳香族类化合物的同分异构体有多少种?
解析: 抠除酯基中的CO后,两个分子“构件”有12种组合,如表7所示。
根据分类加法计数原理,把12种组合的同分异构体数目加起来即得符合条件的同分异构体总数——117种。
恩格斯说:“科学之所以成为科学是因为应用了数学。”化学不能排斥数学,相反,要习惯运用数学的知识、数学的观念去解决化学问题。如在定量实验中运用回归直线方程解决化学问题;在计算化学中运用热力学数据判断反应的可行性问题;在医药制造和材料合成中运用计算机程序设计有机物分子可能结构并运用数学手段筛选具备一定结构特点的有机物目标分子和可能可行的合成路线。本文运用数学计数原理解决有机物同分异构体数目判断问题,并非纯数学运算,依据题给限定条件推理有机物的可能结构对考生有机化学知识的熟练程度提出较高要求,因而运用本文述及的方法解决此类问题不会削弱试题对考生必备知识和学科能力的考查。另外,这两个数学原理虽对部分化学教师而言有些陌生,但对于参加高考的学生而言因高中数学课上刚学过,高考前又复习过,可谓轻车熟路,教学实践也不止一届证明运用数学计数原理解决同分异构体数目的判断问题是可行的。
参考文献:
[1][2]李勇. 普通高中课程标准实验教科书·数学选修2[M]. 北京: 人民教育出版社, 2009: 2~5.
[3]霍本斌. 再谈如何确定有机物同分异构体的数量[J]. 化学教学, 2013, (10): 64.
[4]周伟华. 限定条件下单苯环有机物同分异构体书写与判断[J]. 中学化学, 2018, (6): 47~48.
[5]朱建兵, 袁春仙, 王秋霞. 有限制条件的同分异构体书写策略[J]. 化学教学, 2012, (8): 62~63.

