宇称时间对称光学体系设计及光传输数值实验
展凯云,刘 冰,焦志勇
(中国石油大学(华东)理学院,山东青岛 266580)
0 引言
宇称时间(Parity-Tme,PT)对称系统中的光波传播动力学行为,由于其独特的物理性质和潜在的应用,成为近几年非线性物理中一个备受关注的课题[1]。量子力学表明,对于非厄米哈密顿量,如果系统满足宇称时间对称性,在一定的参数范围内,也可以有一个完全实数的功率谱,这就要求物理系统复势的实部和虚部分别是坐标的偶函数和奇函数,需要说明的是该物理条件是必要但不充分的[2]。实验表明,宇称时间对称系统可通过光学手段来实现[3],即通过控制光学材料的复介电常数来调控,由于复介电常数的实部和虚部分别对应于材料的折射率和损耗/增益,为了满足宇称时间对称性的要求,必须保证折射率是坐标的偶函数,而损耗/增益是坐标的奇函数。光学框架内复杂宇称时间对称势的实现为新颖光学控制方案的提供铺平了道路,获得了许多新颖的光传输特性和规律[4-8],但是该类宇称时间对称系统的实现方法较为复杂,工艺要求高,调控自由度较小,使得光束在宇称时间对称系统中传输动力学行为的研究主要停留在理论预测方面。为了减少复杂光学系统的实验难度和限制,最近几年兴起了一类新的人工网络晶格的实现技术,该类技术是利用一个耦合器连接两个可耦合的光纤环路构成,利用光纤时间复用技术,可以灵活地构造各类人工晶格,为研究周期离散结构中的光束传输动力学行为提供了灵活可调的宏观实验平台。研究者相继在该类系统中观测到了多种光束传输动力学行为,如离散衍射、泰伯效应、布洛赫振荡[9]、局域模[10]、表面态[11]等现象。另外,基于该技术,通过两次周期性的交换其损耗/增益路径也实现了宇称时间对称系统[12-14]。
本文讨论了采用光纤时间复用技术,利用耦合光纤环路设计宇称时间对称光子体系的方法,利用Matlab软件分析了系统参数对该类光学系统能带结构的影响,并数值模拟了高斯光束和周期光场在该类光学系统中的传输特性。结果表明,通过适当选择增损耗/益系数、光纤耦合系数、相位调制参数可以实现对宇称时间对称光学体系能带结构及光传输特性的有效控制,最终形成了一套宇称时间对称光学体系的设计及光传输数值模拟实验方法。
1 宇称时间对称光学系统数值实验
1.1 实验构造
时间复用技术配置图如图1(a)所示,该系统由两个长度相差为ΔL耦合光纤环路构成,它们通过耦合强度为θ的定向耦合器进行耦合。当一个初始光信号入射进入该系统,经过耦合器之后分离成两个信号,然后分别沿着长、短光纤环传播,从而实现左右位置的横向耦合,如图1(b)所示,对应于相应的空间光学网络晶格的横向离散坐标n。两光纤长度差值将产生离散化的到达时间间隔,通过监测这些环路中的往返次数m,获得时间上的独立离散化。利用电光调制器和波形发生器可以精确控制光路上的相位φn,光脉冲振幅调制的微调可以通过声光调制器来实现,从而有效控制环路中的损耗/增益因子γ。该类时间晶格在空间上的等效结构见图1(b),通过使用周期性离散的波导阵列耦合而成,每个阵列位置n上可引入调制相位φn。研究表明,通过选择合适的系统参数可实现宇称时间对称光学体系能带结构的有效控制。

图1 双光纤耦合配置图(a)和宇称时间对称系统(b)
1.2 理论模型
为了实现宇称时间对称性结构,要求势函数的虚部即增益/损耗必须满足奇对称,可以通过声光调制器调制环路的增益因子在γ 和-γ 之间交替变化,此时该类系统中光束演化可用下面的迭代方程定量表示[9,12]:

式中:、分别表示离散传播距离m,波导阵列n处,长、短光纤环路中的光电场幅值。另一方面,为了实现系统全局宇称时间对称性要求势函数实部的偶对称性,可以调控相位值满足关系:

式中:K为整数;φ0为选定的调制相位值。
为了分析该类光学系统的能带结构,引入下面的试探平面波解:

式中:β表示纵向波数,即平面波的传播常数;k为横向波数,相当于空间周期晶格的布洛赫动量。对于考虑的宇称时间对称光学体系来讲,每个原包中含有8 个独立的格点,如图1(b)中红色矩形方框所示。所以系统的光传输动力学行为需要16 个方程来描述,这些方程可用下列耦合方程来描述:
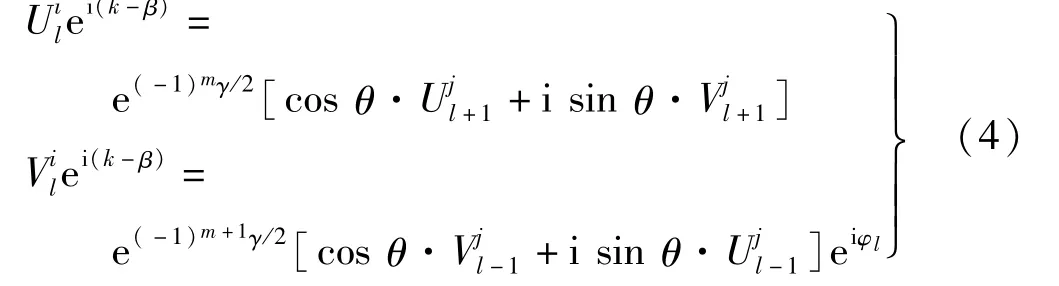
式中:l=n-1,n,n+1,n+2;i,j=m,m+1,并且i≠j。通过数值求解上述耦合方程可以得到能带结构随增益/损耗系数γ、光纤耦合系数θ、相位调制参数φ0的变化规律,从而数值阐明该类宇称时间对称光学体系的能带结构特性。
2 宇称时间对称光学体系能带结构分析
2.1 能带结构随γ的变化规律
图2 所示为θ=π/3,φ0=π/6 时,不同增益/损耗系数下的能级结构变化图。黑色和红色实线分别表示能量谱的实部和虚部。由于光学系统结构的周期性,能级结构在纵向(m)和横向(n)向上均具有周期性,其周期分别为π和π/2,所以本文只给出了第一布里渊区β∈[-π/2,π/2],k∈[-π/4,π/4]内能级结构图。显然,存在4 个能级,相对于β=0,k=0 均具有对称性。当γ值较小时,整个能带的本征值均为实数,随着γ的增大,处于正、负能量区的能级逐渐远离中心,但是处于正、负能量区域内的两条能级之间的间隔逐步减小(见图2(a)和(b))。当γPT=0.55 时,上、下两条能级在布里渊区边缘(k=-π/4,π/4)发生了简并,此时对应着宇称时间对称系统的相变点(见图2(c))。当γ >0.55,能带结构的虚部开始大于0(见图2(d)),当0.55 <γ <0.795 5 时,能带结构是部分复数的。另外,损耗/增益系数存在另外一个临界值γCI=0.795 5,当γ >γCI时,整个能带结构所有的能级值均是复数。显然,能带结构随着增益/损耗系数γ的增大的变化规律为:全部实能量谱→部分复能量谱→全部复能量谱。
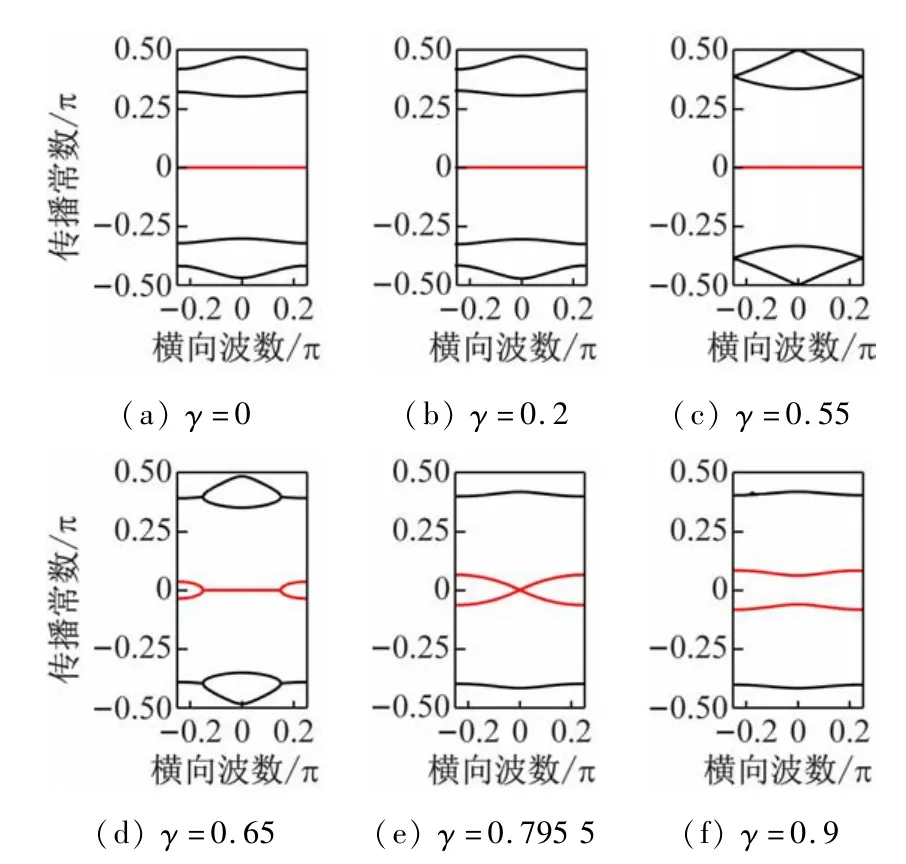
图2 θ=π/3时,不同增益/损耗系数的能带结构
通过改变系统参数进一步研究能带结构随γ的变化规律,如图3 所示。与图2 相比,固定φ0值,选取不同的耦合强度,θ=0.26π,此时能带结构变化规律与图2 情况类似,仍然存在4 个相对于β=0,k=0 均对称的能级。随着γ的增加,能带结构的变化规律仍然为:全部实能量谱→部分复能量谱→全部复能量谱,即能带结构变化过程存在3 个阶段,当γ <γPT=0.233时,整个能带谱均为实数[见图3(a),(b)],当γPT<γ <γCI=1.34 时[见图3(c),(d)],能带结构是部分复数的,而在γ >γCI范围内[见图3(e),(f)],整个能带谱均为复数。图3 与图2 的不同点在于,随着γ 的增加,简并点出现的位置不同,当θ=0.26π,γPT=0.233 时,最上端和最低端的两条能级在布里渊区中心(k=0)开始发生简并,如图3(c)所示,随后在正、负传播常数区域的两条能级才会在布里渊区边缘发生简并[见图3(d)]。
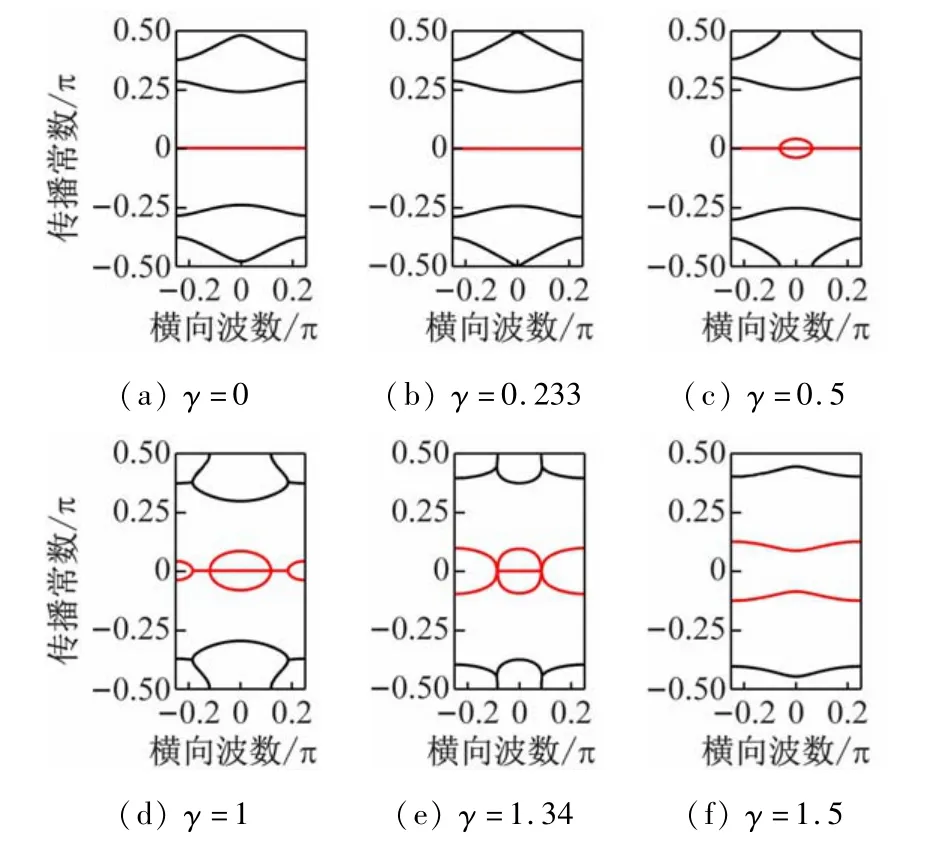
图3 当θ=0.26π时,不同增益/损耗系数的能带结构
2.2 能带结构随耦合强度θ的变化规律
下面研究宇称时间对称光学体系的能带结构随耦合强度θ的变化规律。当φ0=π/6,γ=0.5 时,不同耦合强度θ=0,0.15π,0.25π,0.347π,0.36π,0.377 6π,0.5π和0.64π的能带结构分别绘制在图4(a)~(h)中。当θ=0 时,两个光纤回路之间没有任何的耦合过程,整个系统退化为只含有长光纤环路的光纤系统,此时系统禁带宽度为0。当θ >0 时,布里渊区边缘处能级发生分裂,而布里渊区中心处能级简并程度加强,使得能量谱为部分复数[见图4(b)],当θ=0.25π时,虚部值达到最大值,之后,虚部的幅值逐步降低,当θPT1=0.334π 时,能谱的第1 相变点出现[见图4(c)],也就是说能量谱开始变为全部实数,该特性一直持续到第2 个相变点θPT1=0.347π[见图4(d)],之后,能级开始在布里渊区边缘处发生简并,相应的能量谱又变为部分复数,如图4(e)所示,当θ >θCI=0.377 6π时能带结构变为全部复数能量谱[见图4(g)]。显然在0~0.5π 范围内,能带结构随耦合强度θ的变化规律为部分复数能量谱→全部实能量谱→部分复能量谱→全部复能量谱。根据能带结构的周期性,当θ >0.5π时,能量谱会重复上述过程,如图4(h)所示,当θ=0.64π时其能带结构与θ=0.36π时的能带结构完全相同。

图4 当φ0=π/6时,不同耦合强度的能带结构
图5 为结构参数φ0=0.4π和γ=0.5 时,不同耦合强度θ的能带结构图。研究结果表明第1 个相变点发生在θPT=0.347π 处,当θ <0.347π 时能带为全实数(见图5(b))。当γPT<γ <γCI=0.360 8π时(见图5(d)),能带结构是部分复数的,而在γ >γCI范围内(见图5(e)、(f)),整个能带谱均为复数。该类情况下能带结构随耦合强度θ的变化规律为全部实能量谱→部分复能量谱→全部复能量谱。图5(g)和(h)分别为θ=0.645π和θ=0.8π时的能带图,由于其周期性,它们与θ=0.355π 和θ=0.2π 时的能带图结构完全相同。此外,不同于图4 情况,当φ0=0.4π和γ=0.5时,位于正、负能量谱区域的两条能级相对于各自的带隙中心具有对称性。

图5 当φ0=0.4π时,不同耦合强度的能带结构
2.3 能带结构随φ0 的变化规律
固定损耗/增益系数γ=0.5,图6 给出了当θ=π/3 时,不同相位调制参数φ0的能带结构图。结果表明,当θ=π/3 时,在0~π 范围内能带结构随相位调制参数φ0的变化规律为部分复能量谱→全部实能量谱→部分复能量谱。两个相变点分别为φ0PT=0.266π和φ0PT=0.834π,当φ0<0.266π和φ0>0.834π时能带为部分复能量谱(见图6(a)、(b)、(h)),另外,处于正、负能带区域的两条能级不存在水平对称轴。当0.266π <γ <0.834π时(见图6(c)~(g)),能带结构是全部实数的,而且正、负能带区域的两条能级相对于其带隙中心具有对称性。另一个显著的特点是当选择φ0=π/2 两侧两个距离相同的相位调制参数φ0时,正、负能带区域的能级分别相对于β=0.25π 和-0.25π对称,如图6(b)、(h)和图6(c)、(g)所示。

图6 θ=π/3时,不同相位调制参数对应的能带结构
图7 为当θ=0.36π,γ=0.5 时,不同相位调制参数对应的能带结构图。与图6 对比,能带结构相对于φ0=π/2 仍然具有对称性,但是不同的是,当θ=0.36π时,能带结构在整个相位φ0的变化范围内,不存在完全的实能量谱值。当φ0=0 时,能级简并发生在布里渊中心区域,随着相位参数的增加,能级开始在布里渊边缘发生简并,当φ0=0.5π,能带结构变为全复数,之后能带结构又变为部分复数,显然在整个变化区域部分复数能量谱主要来自能级在布里渊边缘处的简并带来的。

图7 θ=0.36π时,不同相位调制参数对应的能带结构
3 宇称时间对称光学系统中光传输特性
3.1 点光源光束传输特性
选取一个点光源在n=0 格点处入射该光学体系,固定增益/损耗系数、光纤耦合系数、相位调制参数其中的两个,改变第3 个体系参数,相应的光束传输特性如图8 所示,最上一行为当θ=π/3、φ0=π/6 时,不同增益/损耗系数γ=0.2、0.55 和0.6 的光束强度演化图;中间一行为当φ0=π/6、γ=0.5 时,不同耦合强度θ=0.2π、0.34π和0.36π 的光束强度演化图;第3 行为当θ=π/3、γ=0.5 时,不同相位调制参数φ0=0.1π、0.3π和0.7π的光束强度演化图。与上述能带结构讨论类似,选择其能量谱分别为全实数或者复数时的情况。由该图可知,对于特定的体系参数,当相应的能量谱为全实数时,宇称时间对称性得以维持,光束能量能够连续的色散(衍射)至相邻晶格,表现为典型的线性展宽现象,如图8(a)、(e)、(h)、(i)所示;而当系统宇称时间对称性被破坏以后,光束能量不仅分散而且随着距离呈指数增长。在数值模拟过程中,选择了很多的系统参数,研究结果表明,光束的演化规律均表现出上述特性。

图8 点光源光束传输特性
3.2 周期性光场传输特性
周期性光场在空间传输时可表现为自成像现象,即经过一定的纵向传播距离后初始光场分布会完全重现,该现象又称之为泰伯效应,相应的光场重现处的距离称之为泰伯长度或自成像距离[15]。而对于离散波导来讲,理论和实验表明,当激发的波导周期为特定值时,也可以在波导观测到离散的自成像现象[16]。下面简单阐明在本文中设计的宇称时间对称光学体系,当入射的周期性光场周期N=4 时,通过选择合适的体系参数时也会观测到自成像现象。图9 给出了周期性光场传输过程中光强演化图,白色虚线为相应的自成像位置。当γ=0.2、θ=π/3 和φ0=π/6,周期性光场的自成像效应,其泰伯长度为mT=36,而当选择γ=0.2,θ=π/3,φ0=π/2,和γ=0.4,θ=π/4,φ0=π/2,时其泰伯长度大约都为mT=75,但是传播过程中光强分布发生了明显的变化。这就表明,通过选择合适的系统参数可以观测到光场分布和泰伯长度不同的自成像现象。

图9 周期性光场传输特性
4 结语
本文分析了一种采用光纤时间复用技术,利用耦合光纤环路设计宇称时间对称光学体系的方法。利用Matlab软件,系统讨论了该系统的能带结构,通过引入增益/损耗系数、光纤耦合系数、相位调制参数3 个系统参数实现了该类系统能带结构的有效控制;数值模拟了点光源光束和周期光场在该类系统中的传输特性,结果表明,通过适当选择系统参数可观测到光场分布和泰伯长度不同的自成像现象。该类宇称时间对称光学体系实现方法具有实现方法简单、调控自由度高等特点。基于该系统,人们可以进一步研究其他的一些光学现象如布洛赫振动、光局域效应等。该文形成了一套宇称时间对称光学体系的设计及光传输数值模拟实验方法,为人们系统认识宇称时间对称体系的特性及光波传播动力学行为提供了新的方法。

