基于改进TOPSIS的驾驶行为实时安全性评估方法

刘志强，王 涛

(江苏大学 汽车与交通工程学院， 江苏 镇江 212013)

近年来，我国汽车工业快速发展，如何有效减少道路交通事故，提高道路交通安全成为一大难题。在人-车-路系统中，驾驶人是道路交通系统的主体，驾驶人的行为也在很大程度上影响了道路交通安全。因此，国内外众多学者都将研究的重点放在了驾驶人的行为研究上，探究驾驶行为与事故风险之间的关系，预测行驶中车辆的驾驶风险，有助于对个人驾驶行为的安全性进行评估，对相对安全和不安全的驾驶人进行区分[1-2]。目前，由于驾驶行为数据采集方法的多样性和道路交通智能化的发展，基于大数据和便携设备的实时驾驶行为安全性评估将成为一种趋势，能在一定程度上提高驾驶人安全意识和车辆行驶安全性。

咸化彩[3]将驾驶人视觉行为和车辆运行状态参数相结合，通过方差分析和相关性分析确定评价指标，通过模糊网络分析法对次任务驾驶安全性进行了评价。吴紫恒等[4]先利用FCM方法对驾驶行为数据进行初始聚类，接着用BP神经网络进行学习，然后用得到的分类器对驾驶行为进行实时分类，完成了驾驶行为的客观评价。

Shi等[5]先从车辆轨迹数据中提取大量驾驶行为特征，然后利用XGBoost方法构建行为特征和相应风险等级之间的关系，根据特征重要性排序筛选出关键行为特征，最后用关键特征预测行驶中车辆的风险等级，准确度达到89%。Brombacher等[6]用径向基网络对驾驶行为进行建模，结合支持向量机SVM方法实现了对正常驾驶行为和分心驾驶行为的分类。根据目前国内外学者对于驾驶行为的相关研究，实验设计方案不够完善，对驾驶行为安全性表征指标的分析和建模的研究也有所欠缺，所建立的驾驶行为安全性评价指标体系不够完整，安全性评估也不够准确[7-8]。

因此本文从驾驶人视觉感知行为、驾驶人操纵行为和车辆运行状态3个方面对可能影响驾驶安全性的因素进行分析，初步建立驾驶行为安全性评估指标体系，然后利用Pearson相关性分析确定了9个用于进行安全性评估的关键指标，接着通过层次分析法和熵值法结合对各个评估指标赋权，最后利用马氏距离和联系向量距离的独特优势改进传统的TOPSIS多属性决策方法，在评估准确性上有了较大提高，为驾驶行为安全性评估提供了新的思路。驾驶行为安全性评估流程如图1所示。

图1 驾驶行为安全性评估流程框图

1 实验设计与数据采集

由于驾驶模拟器的体验感较差，与真实道路交通条件相比，不能准确掌握驾驶人的行车状态，本文通过实车试验的方式采集安全性评估所需的各类数据。试验车辆集成了CAN总线车辆运行状态数据采集系统和驾驶人眼动信息采集系统，对相同道路交通环境下，不同驾驶人行为的安全性进行分析。所选择的试验路段为镇江市某快速公路，全程28 km，行车时间约40 min。试验车辆装备有毫米波雷达、摄像头、行车记录仪、Smart-eyes眼动仪、方向盘转角传感器、轮速传感器、GPS等(见图2)。其中工控机负责记录各类数据，并将各信号集中转换，实现数据的同步输出。本试验共招募10名驾驶员作为实验对象，其中男6人，女4人，均持有C1驾驶证，年龄在26～40岁，驾龄在5～10 a，参与实验的驾驶员均视力良好，无酒精等影响。

图2 试验车与数据采集设备

2 驾驶行为安全性评估指标体系

2.1 变换车道视觉感知行为安全性指标

在正常驾驶过程中，驾驶人所获取的道路交通信息绝大部分来自于视觉[9]。在道路交通条件相同的情况下，不同驾驶人在跟车距离、注视区域等方面都有很大差异，最终影响车辆行驶稳定性和安全性。本文利用K-means方法对通过眼动仪采集的10名驾驶人注视点数据进行聚类，将驾驶人换道过程的注视区域划分为5块，结果如图3所示(车道正前方、车道左前方、车道右前方、左后视镜和右后视镜)。

图3中，X为水平方向注视点位置，Y为竖直方向注视点位置。

图3 驾驶人注视区域划分结果

通过对驾驶人注视点位置的聚类分析，左侧换道过程与右侧换道过程的视点分布均呈现出一定的规律。因此，为研究不同驾驶人换道过程的视觉变化特征，本文对10名驾驶人在要求规范性变换车道情况下，注视不同位置的平均次数进行统计分析，结果如表1、2所示。

表1 左侧变换车道驾驶人对不同位置的平均注视次数

将直行与换道过程中驾驶人注视不同位置的平均次数进行对比，发现存在明显的差异。因此，本文选择左侧换道驾驶人注视左后视镜和车道左前方的平均次数，右侧换道注视右后视镜和车道右前方的平均次数，作为分析驾驶人变换车道视觉感知行为安全性的指标。

经过分析，本文提出利用每一位驾驶人换道过程观测不同位置的次数与样本中规范性要求下变换车道注视行为水平均值进行对比，得到驾驶人变换车道视觉感知行为安全性指标(LCTR)。

LCTR=F/A

(1)

式中：F为各驾驶人换道过程观测不同区域的总次数；A为规范性要求下变换车道注视行为水平均值(左侧换道注视左后视镜和车道左前方的平均次数，右侧换道注视右后视镜和车道右前方的平均次数)。

若LCTR=1，说明该驾驶人换道视觉行为特性与规范性要求一致，而LCTR>1或LCTR<1都说明该驾驶人换道视觉感知行为安全性降低。

2.2 前方障碍物感知安全性指标

2.2.1驾驶人前视预瞄距离

如图4所示，可利用驾驶人视线点在世界坐标系下的投影，通过三角函数关系计算得到预瞄点与驾驶人之间的距离[10]。

图4 世界坐标系下驾驶人前视预瞄距离示意图

图4中，E为驾驶人的视线源，G为驾驶人的前视预瞄点，EG为驾驶人的视线方向，df为驾驶人前视预瞄距离。

(2)

式中：GazeOrigin.y为视点位置的y方向坐标；h为地面与世界坐标系水平面的垂直距离；GazeDirection.y为世界坐标系下视线在y方向的单位分量；GazeDirection.z为世界坐标系下视线在z方向的单位分量。

2.2.2安全制动距离

目前的安全制动距离模型[11]有很多，本文采用的安全制动距离公式是：

(3)

式中：S为安全制动距离；v为自车车速;vrel为相对速度；t1为驾驶人的反应时间(取0.1 s)；t2为制动器延迟时间(取0.6 s)；a1为自车最大减速度(取6 m/s2)；a2为前方障碍物最大减速度(取8 m/s2)；d0为最小停车距离(取3 m)。

本文通过安全制动距离与驾驶人前视预瞄距离的比值(OSIA)表征驾驶人在直行过程中对前方障碍物视觉感知行为的安全性：

(4)

式中：S为安全制动距离；df为驾驶人前视预瞄距离。

若OSIA<1，说明前视预瞄距离大于安全制动距离，进行紧急制动所需距离足够，安全性较高；若OSIA>1，则说明前视预瞄距离小于安全制动距离，进行紧急制动已没有足够距离，安全性较低。

2.3 驾驶人操纵行为安全性指标

2.3.1纵向操纵行为安全性

纵向操纵行为安全性指标主要表现为制动幅值变化率(BACV),在采样时间周期T内的制动幅值变化率可以反映出一段时间周期内制动行为的急缓程度。计算式如下：

(5)

式中：b(n)为制动幅值采样样本；T为采样时间周期。

2.3.2横向操纵行为安全性

横向操纵行为安全性指标主要表现为方向盘转角熵值(SE)，方向盘转角熵值越大，说明驾驶人的横向操纵行为越不稳定，进一步影响行车安全性[12]。SE是根据方向盘转角的预测偏差出现的概率来计算的，θ(n)是t(n)时刻方向盘转角的实际值，θp(n)是根据泰勒公式展开计算得到的预测值。

具体计算式如下：

θp(n)=θ(n-1)+(θ(n-1)-θ(n-2))+

(6)

则方向盘转角的预测偏差为：

e(n)=θ(n)-θp(n)

(7)

为方便进行计算和分析，将方向盘转角预测误差值划分为9个区域(P1～P9)。其中有90%的预测误差值落在[-α，+α]，根据误差值落在各个区间的频数确定各区间的概率分布值Pi，方向盘转角熵值计算式如下：

(8)

SE反映出驾驶人在任意时刻转动方向盘角度预测误差值分布情况的不确定性，熵值越小说明驾驶人横向操纵行为安全性越高，熵值越大则说明安全性越低。

2.4 车辆运行状态安全性指标

2.4.1纵向运行状态安全性

1) 纵向速度标准差

(9)

2) 纵向加速度标准差

(10)

3) 纵向加速度变化率

急加速行为也是一种影响驾驶安全的因素，而采样时间段内纵向加速度的变化率可以反映出一段时间内加速的急缓程度。计算式如下：

(11)

式中：a(i)为纵向加速度采样样本；采样时间段长度为T。

2.4.2横向运行状态安全性

1) 方向盘转角标准差

车辆的横向运动是由于驾驶人对方向盘的操作产生的。目前，驾驶员的转向稳定性主要通过分析一段时间内方向盘转角的离散度来评估。计算式如下：

(12)

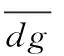
2) 横向加速度标准差

(13)

3) 横向车道保持安全性指标

在驾驶过程中，如果车辆的横向偏移量过大，会造成压线行驶，形成安全隐患，严重影响行车安全。因此，本文通过横向偏移距离均值占所在车道宽度百分比指标(LKSR)来表征驾驶人横向车道保持安全性。

(14)

式中：dl(i)为车辆中心轴到左侧车道线的距离；dr(i)为车辆中心轴到右侧车道线的距离；设dl(i)≤0,dr(i)≥0。

3 确定关键指标与指标权重

在一个评价集中，评价指标之间会存在某种联系，利用Pearson相关性分析可得到指标之间是否存在过强的关联性，如果指标间的关联性过强，会造成指标的冗余，计算量增加[13]。因此，本文通过Pearson相关性分析，保留关键指标，减少计算的复杂度。

通过相关性分析可以发现，纵向速度标准差和纵向加速度标准差的相关系数为0.289，相关性较高，又属于同一类指标，因此保留纵向速度标准差指标，去除纵向加速度标准差指标，最后得到9个用于安全性评估的关键指标：变换车道视觉感知行为安全性指标、前方障碍物感知安全性指标、制动幅值变化率、方向盘转角熵值、纵向速度标准差、纵向加速度变化率、方向盘转角标准差、横向加速度标准差和横向车道保持安全性。具体数据如表3所示。

表3 计算得到的10名驾驶人各指标数据

表3中，LCTR为变换车道视觉感知行为安全性指标、OSIA为前方障碍物视觉感知安全性指标、BACV为制动幅值变化率、SE为方向盘转角熵值、AWSTD为方向盘转角标准差、LASTD为横向加速度标准差、LKSR为横向车道保持安全性指标、VSTD为纵向速度标准差、LACR为纵向加速度变化率。

3.1 层次分析法(AHP)

在得到9个关键指标之后，需要对各个评估指标进行赋权，目前主要从主观和客观两方面对评估指标进行赋权。本文在咨询专家意见之后采用层次分析法确定主观权重。

首先，需要构造判断矩阵，一般采用9级标度来表示不同指标之间的相对重要程度。若上一层指标支配的下一层指标有n个，那这n个指标就构成一个两两比较的判断矩阵A=(aij)n×n，其中，aij表示指标i与指标j的重要性之比。

其次，在计算得到指标权重系数之后，必须进行一致性检验，当随机一致性比例CR<0.1时，认为判断矩阵具有一致性。若一致性检验通过，说明该权重系数符合要求，否则需要调整判断矩阵重新计算。

经过计算得到9个指标主观权重：

[0.143 1 0.214 7 0.119 3 0.119 3 0.053 8

0.080 7 0.134 6 0.080 7 0.053 8]

3.2 熵值法

熵值法是一种客观赋权法，根据各项指标原始数据所提供的信息量来确定指标权重[14]。熵值法确定客观权重的步骤如下：

1) 计算第j项指标下，第i个对象的特征比重：

(15)

2) 计算第j项指标的熵值：

(16)

3) 计算指标的差异性系数：

gj=1-ej

(17)

4) 确定权重：

(18)

乘法集成综合权重：

(19)

式中：pj和qj分别为通过主观赋权方法和客观赋权方法得到的指标权重。

最终得到9个评估指标的综合权重：[0.142 5 0.247 3 0.065 1 0.126 6 0.051 1 0.078 1 0.168 8 0.050 7 0.069 8]

4 TOPSIS多属性决策方法

作为一种多属性决策方法，TOPSIS的原理是通过计算各评估对象与理想化目标的相对贴近度来进行相对优劣排序，其中理想化目标包含了正理想解S+和负理想解S-。正理想解是待评估方案集中的最优解，它表示各个单一指标值都达到了方案集中的最优，而负理想解则是所有待评估方案中的最劣解[15]。

设有m个驾驶人A1,A2,…,Am，n个评估指标C1,C2,…,Cn，Xij是第i个驾驶人Ai的第j项指标值。利用TOPSIS方法进行多属性决策的原理如下：

1) 根据原始数据建立决策矩阵：

(20)

2) 由于不同指标数据的量纲存在差异，需要规范化处理，得到规范化矩阵σ：

(21)

3) 对各指标赋权，将规范化指标数据矩阵乘以权重矩阵，得到评估矩阵V：

(22)

4) 确定正理想解S+和负理想解S-：

(23)

若指标Cj为效益型指标，则：

若指标Cj为成本型指标，则：

5) 分别计算各驾驶人到正负理想解的距离：

(24)

(25)

(26)

传统的TOPSIS多属性决策方法所使用的距离计算公式是欧氏距离，不能考虑评估指标存在相关性时带来的影响，而驾驶行为安全性表征指标之间存在一定的相关性，因此会造成评估结果不准确。同时，还会出现某评估对象与正负理想解的距离都近的问题，所以也不能对评估对象的相对优劣进行客观合理的评估。考虑到传统方法的一些局限性，本文从以下两方面进行改进。

4.1 马氏距离改进原理

马氏距离是一种既不受指标之间的相关性影响，也不受指标量纲影响的距离计算方式，这种优良特性可以使改进之后的多属性决策更加科学、有效[16]。

假设第i个评估对象的指标向量为：

Xi=(Xi1,Xi2,…,Xin)

(27)

(28)

(29)

式(28)(29)分别为正负理想解所对应的空间坐标。

则第i个评估对象到正负理想解的马氏距离分别为：

(30)

(31)

式中：Σ为相关系数矩阵。

4.2 联系向量距离改进原理

定义1设集合A0和B1的联系度为(A0～B1)=a+bi+cj,其中，a为同一度，b为差异度，c为对立度，则向量(a,b,c)为集合A0和B1的联系向量。记为μ=(a,b,c)。

定义2设集合A0和Bs的联系向量为μs=(as,bs,cs)，集合A0和Bk的联系向量为μk=(ak,bk,ck)，则集合Bs和Bk的联系向量距离为：

(32)

根据集对分析思想[17]，我们把正负理想解看成是确定与不确定系统中相互对立的关系。所以需要计算各个评估对象与正负理想解的联系度_k+、_k-。

若评估指标为效益型指标，由评估对象Ak和正理想解S+组成集对H+=(Ak,S+)，则联系度计算方式如下：

(33)

k=1,2,…,m;t=1,2,…,n

(34)

同理可计算评估对象Ak与负理想解S-的联系度，由评估对象Ak与负理想解组成集对H-=(Ak,S-)，则有：

(35)

k=1,2,…,m;t=1,2,…,n

(36)

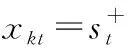
若评估指标为成本型指标，则联系度计算方式与效益型指标恰好相反。

根据前面的定义，评估对象Ak到正负理想解的联系向量距离计算式如下：

(37)

(38)

4.3 改进TOPSIS多属性决策方法

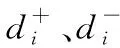
(39)

(40)

式中：α+β=1，具体数值由决策者决定，本文取α=β=0.5。

则各驾驶人与理想解的相对贴近度为：

(41)

这样计算得到新相对贴近度,克服了传统TOPSIS多属性决策方法在距离计算方式上的2个缺陷，使评估结果更加科学、合理。

最后，根据相对贴近度Ci的大小对10名驾驶人进行驾驶行为的安全等级排序，Ci值越趋近于1，说明该评估对象的驾驶行为安全等级越高。

4.4 综合评估结果分析

表4中，累计违章次数为10名驾驶人近3年的累计驾驶违章次数统计数据。

表4 驾驶行为安全等级排序结果

通过分析以上数据可以发现，10名驾驶人行为的安全等级排序为3>6>7>5>1>8>10>2>9>4。3号驾驶人的行为安全性最高，而4号驾驶人的行为安全性最低。利用Pearson相关性分析，设置显著性水平为0.05，发现传统方法得到的驾驶行为安全等级排序与累计违章次数的相关系数为0.704 6，而改进方法安全等级排序与累计违章次数的相关系数为0.920 1，说明在都通过显著性检验的情况下，改进方法的驾驶行为安全等级排序更准确，证明了本文所提出的改进方法的有效性和准确性。

5 结论

1) 本文提出了一种从3个方面评估驾驶行为安全性的方法：驾驶人视觉感知行为、驾驶人操纵行为与车辆运行状态。对可能影响驾驶安全性的各种因素进行了分析，完善了驾驶行为安全性评估指标体系。

2) 本文通过一种马氏距离和联系向量距离结合改进的TOPSIS多属性决策方法进行驾驶行为的安全性评估，利用新的相对贴近度大小进行安全等级排序，提高了评估准确性，为驾驶行为的安全性评估提供了新的思路。

3) 本文提出的改进方法中新的相对贴近度结合了马氏距离和联系向量距离的优势，克服了欧氏距离的局限性，解决了传统的TOPSIS多属性决策方法存在的不足，使改进后的多属性决策方法更加科学合理。