遗传模拟退火算法优化BP 神经网络的GPS 高程拟合

石晨阳，袁晓燕，江志成

( 重庆交通大学，重庆 400074 )

0 引 言

随着卫星导航定位技术的快速发展，GPS 技术在各类工程中应用愈加广泛[1]. GPS 技术可以测得某点的大地高，测绘工程中使用的是正常高，需要使用合适的算法求出高程异常值. 目前高程异常拟合研究方法主要有数学模型拟合法、地球重力场模型法和神经网络方法[2-4].

神经网络能够以任意精度逼近任意连续函数及平方可积函数[5-6]，在高程异常拟合中应用广泛. 魏宗海[7]认为，BP 神经网络层与层之间初始权值和阈值如果设置不合理，将会导致网络收敛速度慢和陷入局部最优解；李明飞等[8]提出用遗传算法优化BP 神经网络(GA-BP)算法进行高程遗传拟合，但是优良个体急增会导致种群失去多样性，过早收敛从而陷入局部最优. 这说明GA-BP 算法需要进行优化，跳出局部最优陷阱.

本文针对传统BP 神经网络和GA-BP 算法的不足，采用遗传模拟退火算法(SA)优化BP 神经网络算法进行高程遗传拟合，在遗传算法的种群更新中加入SA，解决了收敛速度慢、易陷入局部最优的缺陷，精度和效率得到了明显提高，且能基本满足四等水准测量精度要求.

1 基本原理与方法

1.1 BP 模型

BP 神经网络的训练模式是误差反向传播，它的输入层和输出层为一层，隐含层大于或等于一层. 各层之间的权值和阈值由初始化随机得出，通过反复训练得到最优的权值和阈值. 其具体网络结构如图1所示.

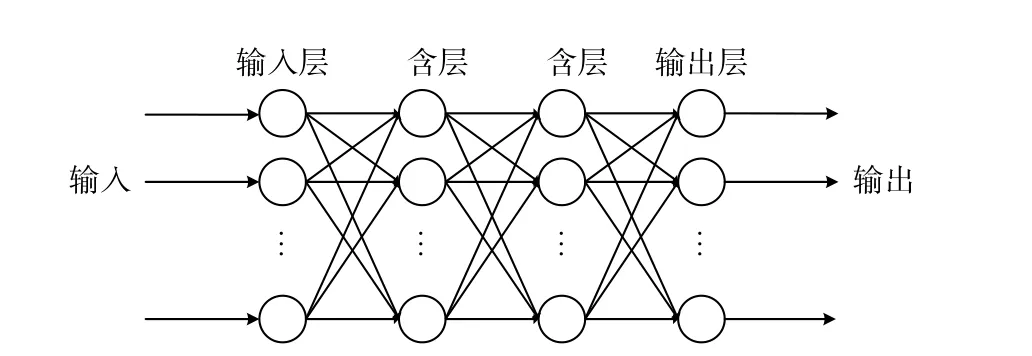
图1 BP 神经网络示意图

下面给出BP 算法步骤[9]：

1)设置各权值和阈值的初始值：wji(0)、θj(0)为小的随机数.

2)提供训练样本：输入矢量Xk，k=1，2，···，p；期望输出dk，k=1，2，···，p；对每个输入样本进行下面步骤3)～步骤5)的迭代.

6)当k每经历1～p后，判断指标是否满足精度要求

1.2 GA-BP 模型

遗传算法(GA)是模拟生物进化过程中基因的遗传、杂交和变异的一种搜索算法. 在寻优过程中，首先寻得一组可行解，保持一组解并重新组合，不断迭代更新直至得到最优解[10].

下面给出GA 算法步骤[11]：

1)确定编码方式，编码方式通常为二进制编码和实数编码.

2)确定适应度函数

4)计算适应度函数的值，如满足约束条件，则算法终止，否则返回到步骤2)继续迭代.

以平面水准坐标X、Y作为输入层，高程异常值作为输出层，以GA 算法的染色体赋值权值和阈值，进行遗传、交叉、变异操作. 当结果满足结束条件时，保留权值和阈值，再对测试集进行训练，达到最终结果.

1.3 GSA-BP 模型

SA 是一种模仿固体退火结晶过程的随机搜索算法. 在寻优过程中，最优解被接受，非最优解根据算法需要也可能被接受，这样就使得算法不易陷入局部最优. GSA-BP 算法就是将SA 算法加入到GA 算法的种群更新中，得到最优解后再进行BP 神经网络训练.

下面给出SA 算法的步骤[12]：

1)参数初始化：包括初始温度T，T需要充分大，初始解状态P，这是算法迭代的起点，每个温度T值下的迭代次数N；

2)当k=1，···，N时进行步骤3)～步骤6)的操作；

3)产生新解P′；

4)计算增量Δt′=C(P′)−C(P)，其中C(P)为评价函数；

5)若Δt′<0 则接受P′作为新的当前解，否则以概率exp(−Δt′/T)接受P′作为新的当前解；

6)如果满足终止条件则输出当前解作为最优解，算法终止，否则返回到步骤2).

GSA-BP 算法具体流程如图2 所示.

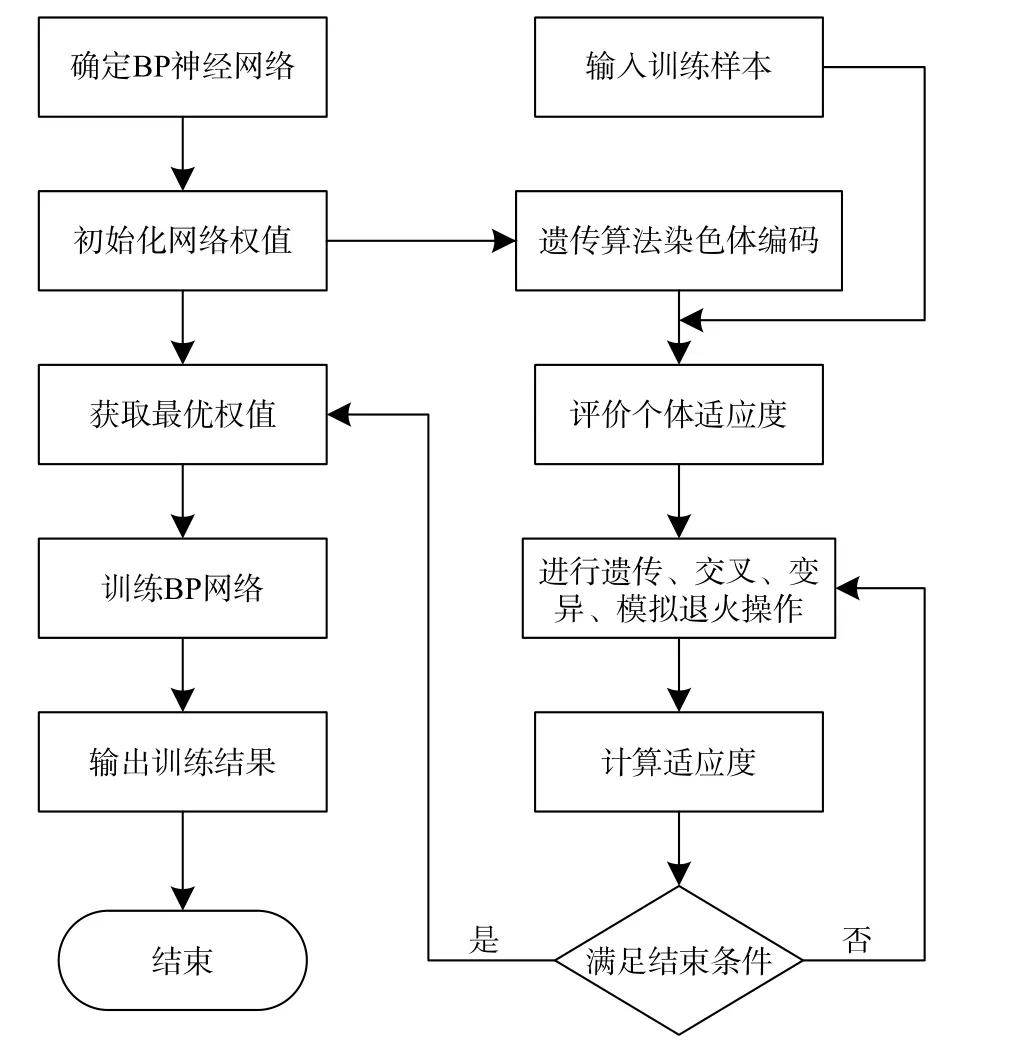
图2 GSA-BP 算法流程图

以平面水准坐标X、Y作为输入层，高程异常值作为输出层，以GA 算法的染色体赋值权值和阈值，进行遗传、交叉、变异、模拟退火操作，当结果满足误差条件时，所得权值和阈值即为最优，以此权值和阈值进行测试集训练，结果即为所得.

2 实验分析

2.1 实验数据介绍

本实验以南方某市E 级GPS 控制网数据为训练数据[13]. 实验区面积约500 km2，共计58 个GPS 点，且已全部进行了四等水准联测. 该实验区点位分布均匀，各点与最近点平均距离为2.1 km. 地形较为平坦，正常高最大值为64.7 m，最小值为9.2 m，平均值为25.7 m. 具体点位分布如图3 所示.

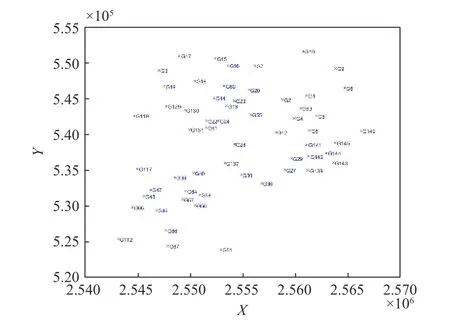
图3 某地区GPS/水准点分布图

2.2 实验结果及分析

用该实验区58 组GPS/水准数据构造21 个训练集A1，A2，···，A21，其中A1={G51，G112，G27，G58， G46， G45， G48， G12， G28， G55， G9， G20，G129，G18，G19，G17，G130，G131，G67，G143，G66，G36，G65，G139，G29，G56，G30，G57}，该28 个点均匀分布. 然后每个训练集依次加入G142，G144，G149，G64，G141，G8，G40，G137，G47，G5，G38，G4，G63，G117，G6，G1，G2，G24，G61，G22，剩下的点作测试集B1，B2，···，B21. 分别使用BP 算法、GABP 算法和GSA-BP 算法对训练集进行训练，再用测试集进行测试. 对结果进行统计分析，结果如表1、图4～5 所示.

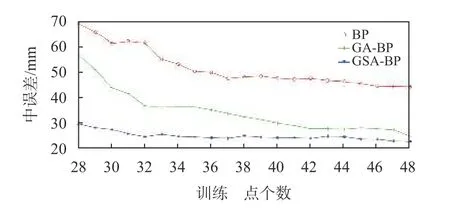
图4 测试集高程异常中误差预测结果对比图

表1 不同训练集点个数下测试结果对比表

由表1、图4～5 可知，当训练集和测试集都相同时，在进行高程异常拟合训练后，GSA-BP 算法的测试集精度比BP 算法要高约52%，比GA-BP 算法高约25%，说明GSA-BP 算法可以有效解决陷入局部最优问题，提高精度；GSA-BP 算法训练时间比BP 算法低约77%，比GA-BP 算法低约39%，说明GSABP 算法可以有效解决收敛速度慢问题.

由图5 可知，随着训练集点个数的增加，三种算法的精度都在提高，但GSA-BP 算法在训练集点个数很少时也能保持很高的精度，说明GSA-BP 算法对训练集点个数要求没有其他两种算法高；在训练集点个数为38 时，三种算法的精度都趋于稳定，精度随训练集点个数的增加变化不大，说明此时网络训练能力已经够饱和.

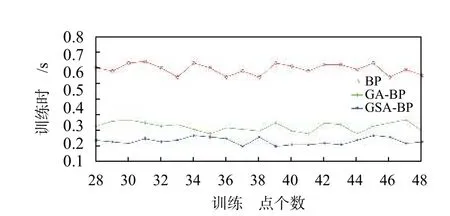
图5 测试集训练时间对比图

因此，以训练集点个数为38 进行训练为例，剩下点作为测试集. 该测试集38 个点均匀分布，点与最近点平均距离为1.9 km. 分别用三种算法进行高程异常拟合，对结果进行统计分析，并与四等水准要求进行比较，结果如表2 和图6 所示.

由表2 和图6 可知，在测试集20 个点位中，BP 算法、GA-BP 算法、GSA-BP 算法高程异常差满足四等水准限差个数分别是13、15、16. GSA-BP 算法在进行高程异常拟合时能基本满足四等水准测量精度要求.

图6 三种算法训练结果对比图

3 结 论

本文通过使用BP 算法、GA-BP 算法、GSA-BP算法进行高程异常拟合，并分别使用不同训练集点个数进行训练测试，比较三种算法的训练结果. 得到如下结论：

1) GSA-BP 算法能有效解决网络收敛速度慢、易陷入局部最优等问题，提高训练精度和效率；

2)当训练样本较少时，GSA-BP 算法也能保持一定的精度；

3) GSA-BP 算法用来进行高程异常拟合，能基本满足四等水准要求，具有可行性.