基于模糊综合评判法的宁南县滑坡易发性评价

刘福臻，王 灵，肖东升，王军朝

(西南石油大学 土木工程与测绘学院，四川 成都 610500)

滑坡易发性评价作为危险性评价和风险性评价的基础，是防灾减灾过程中不可缺少的程序。近年来，随着计算机技术和地理信息技术的快速发展，滑坡的易发性评价逐渐成为了研究热点[1]。但由于滑坡发育的复杂性，目前还没有一套完全成熟的理论能对其进行有效的防治。为此，国内外学者对滑坡的易发性评价开展了一定程度的研究。李环禹等[2]和Kayastha等[3]从因子角度出发，分别探讨了降雨因子和多因子之间的组合对滑坡易发性评价的影响。田述军等[4]和Xiaohui Sun等[5]从评价单元角度出发，论述了斜坡单元和网格单元对评价精度的影响。李文彦等[6]和Bourenane H等[7]从多个模型对比的角度出发，探讨了信息量、频率比、逻辑回归、层次分析法等模型在滑坡易发性评价中的精度表现。Nsengiyumva J B等[8]和孙德亮等[9]以机器学习为基础，探讨了黑箱模型在易发性评价中的应用。以上研究分别从不同角度对滑坡的易发性进行了探索，一定程度上促进了滑坡灾害防治学科的发展，但鲜有学者对滑坡评价因子的量化和模糊综合评价模型的隶属函数作相应的研究。

鉴于此，本文以统计学理论为基础，将历史滑坡点与评价因子的二级属性进行叠加分析，利用相对滑坡点密度作为本次实验的量化值。该方法从数据本身的结构信息出发，实现了滑坡因子二级属性的客观量化。模型上，采用模糊综合评判法作为评价模型，该模型以隶属函数为基础计算出每个评价单元在各分区的概率，通过选择其中最大值所对应的易发性分区作为评价结果，从而很好的解决了评价等级的划分问题[10]。模型的缺陷在于模糊隶属函数的建立存在较强的主观性，且现有的隶属函数都不太适合滑坡的易发性评价。基于此，本文将反距离权重的思想用于确定因子属性的隶属度，探讨该想法在评价过程中的可行性与有效性。

1 研究区概况及数据源

1.1 研究区概况

宁南县位于我国四川省凉山州东南部，是连接川、滇两地的重要通道。研究区内崇山峻岭，沟壑纵横，黑水河贯穿其南北，于宁南县葫芦口处汇入金沙江。研究区气候类型为南亚热带季风气候，具有“一山分四季，十里不同天”的立体特征[11]。复杂多变的地貌和气候特征为该地区提供了丰富的矿产资源，同时也导致了该地区地质灾害的频发。

据宁南县2019年1：5万地质灾害详查显示，全县共有482个地质灾害点。其中滑坡359个，泥石流100个，不稳定斜坡12个，崩塌11个。滑坡占据了所有灾害点的74.5%，是宁南县最主要的地质灾害。

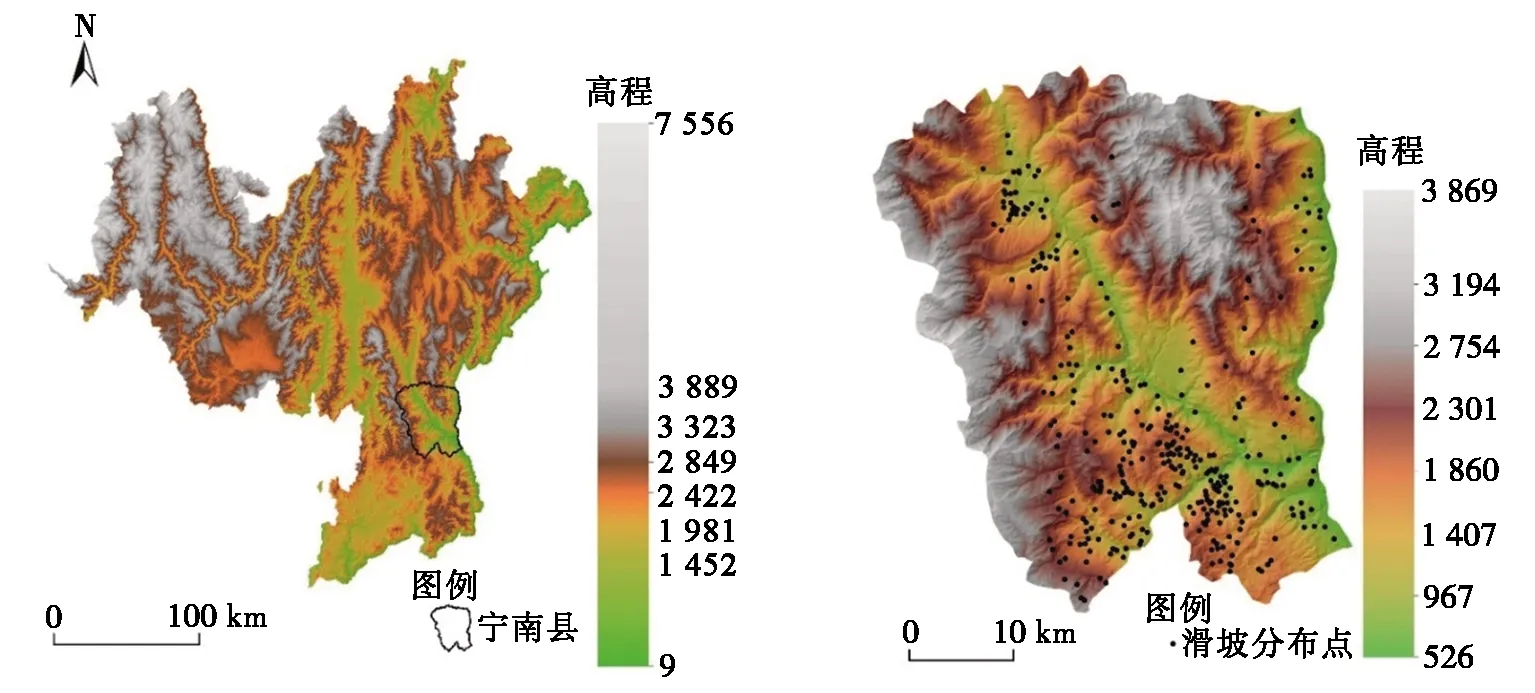
图1 研究区地理位置Fig.1 Geographical location of the study area

1.2 数据源

本文用到的数据主要有滑坡历史灾害点、宁南县DEM、宁南县土地利用覆盖、1∶25万地质图，详细内容见表1。其中滑坡灾害点主要用于和各因子的叠加分析；DEM主要用于高程、坡度、坡向、坡型和水系的提取；1∶25万地质图主要用于地层和断层的提取。将所有图层的投影坐标系设置为WGS_1984_UTM_Zone_47N，并重采样为30*30的栅格单元。

表1 数据源Table 1 Data source

2 模型介绍

2.1 因子正向化(量化)

因子正向化是指将量化的因子转换成与滑坡发生成正相关形式的过程。由于数据的多源性，原数据通常不能直接为我们所用。以连续因子中的坡度为例，宁南县的坡度范围大约为0～75°，然而有利于滑坡发育的范围并不是随着坡度的增加而变大。同理，对于类似坡向、土地利用、岩组等分类数据，都需要将之量化为能表现滑坡易发性指数的形式。因此，本文从统计学原理出发，利用历史滑坡点数据，选取相对滑坡点密度作为各因子的正向化值。相对滑坡点密度计算方法见式(1)。

(1)

式中Xi为因子X在二级属性i下的相对滑坡点密度；ni为因子X在二级属性i下的滑坡个数；si为研究区内因子X在二级属性i下的栅格个数；N为研究区总滑坡个数；S为研究区总栅格数。

2.2 熵权法

Shannon在1948年提出了熵值理论[12]，熵值是对不确定信息的一种度量，对系统或事件离散性和无序性的概述。其主要思想为：指标的变异程度越大，对应的权值也越大。在本文中体现为滑坡因子二级属性值的变异程度。也就是说，对于所有的样本而言，倘若某个因子正向化后的二级属性值都相同，则认为这个指标的权值为0，即该因子对评价系统起不到任何帮助。同理，某个正向化后的因子的属性值变异越大，则该因子对滑坡的影响也就越大[13]。具体计算过程如下：

(1)假设x表示事件X可能发生的某种情况，P(x)表示这种情况发生的概率。

我们可以定义：

I(x)=-ln(P(x)).

(2)

(2)如果事件X可能发生的情况分别为：x1,x2,x3…xm，事件X的信息熵值H(X)可用式(3)计算。

(3)

(3)最后，指标的熵权计算方法见式(4)。

(4)

式中wi为第i个因子的权重；Hi为第i个因子的信息熵；n为评价因子的类别个数。

2.3 模糊综合评判法模型

2.3.1 模糊综合评判法模型介绍

模糊综合评判模型通过对因子的属性做隶属度赋值，以此来达到评判的目的。其核心在于用隶属程度代替属于和不属于，即你有黑的可能性，也有白的可能性[14]。评价过程以隶属函数和指标权重为基准，通过唯一确定评价单元的评判等级，从而解决了指标等级划分问题。具体步骤如下：

(1)设因素集U={u1,u2,u3,…,um}，评价集V={v1,v2,v3, …,vn}。因素论域和评价论域之间的模糊关系用评价矩阵R来表示：

(5)

其中rij=μ(ui,vj)表示从因素ui的角度来判定事件评为vj的隶属度。

(2)给定出影响因子的权重。

W=(w1,w2,w3,…,wi)，其中wi为第i个因子的权重，该权重通过熵权法计算获得。

(3)利用模糊矩阵R和权重矩阵W计算评价集Z。

Z=(z1,z2,z3,…,zn)=W1×m⊙Rm×n.

(6)

(4)最后根据每个评价单元的最大隶属度b来确定评价单元的等级vi。

b=max(z1,z2,z3,…,zn).

(7)

2.3.2 隶属函数的确定

隶属函数的确立，是模糊数学及其应用在理论上和实践中的关键问题[15]。常用的隶属函数有模糊统计法和指派法[16]。然而这些常规的方法都不太适合滑坡的易发性评价。基于滑坡影响因子的复杂性，本文将反距离权重法的思想用于模糊隶属度的计算。过程如下：

(1)利用相对滑坡点密度给每个影响因子的二级属性赋值，并选出与评价等级相匹配的属性值作为相应等级的基准。

(2)对于评价集V={v1,v2,…,v5}，因子ui对应的隶属度rij=μ(ui,vj)的计算方法见式(8)。

ri1=1-|xi-xi1|
ri2=1-|xi-xi2|
ri3=1-|xi-xi3|
ri4=1-|xi-xi4|
ri5=1-|xi-xi5|.

(8)

式中xi是评价因子ui的量化值，xi1,xi2…xi5是评价集v1,v2,…,v5的基准。xi1,xi2…xi5的选择一般由ui量化后，根据从小到大的顺序而定。

3 滑坡分布特征及评价因子量化结果

3.1 坡度

由1∶5万地质灾害详查结果得知，全县76.3%的滑坡在5°到25°的平缓地带。其中5°—15°为量化的峰值。量化结果整体呈现的趋势为：随坡度的增加先变大后减小。研究表明，雨水在缓坡地段容易汇集，使得雨水的渗透作用加强，导致土石层饱和，从而增加了滑体的重量，降低了土石层的抗剪能力[17]。所以宁南县的滑坡主要聚集在平缓地带。坡度较陡的地带大部分为岩质斜坡，通常情况下岩质斜坡在抗剪力上远远超过土质斜坡，这些斜坡往往发育为崩塌，所以在坡度大于45°的研究区内没有滑坡灾害点的分布。本文将研究区坡度分为了[0，5°]、[ 5°，15°]、[ 15°，25°]、[ 25°，35°]、[ 35°，45°]、[ ≥45°]六大类，图2为滑坡坡度分布统计及其量化图。

图2 坡度统计量化结果Fig.2 Statistics and quantitative results of slope

3.2 坡向

利用ARCGIS中的坡向工具将DEM数据转化为坡向数据。宁南县的坡向分为平地、北、东北、东、东南、南、西南、西和西北9大类型。经实地调查发现，在宁南县范围内，除了平地没有滑坡外，各坡向量化的相对滑坡点密度值起伏变化不大。整体的数据走势表明坡向因子在研究区范围内对滑坡的影响较小。图3为坡向分布统计及其量化图。

图3 坡向统计量化结果Fig.3 Statistics and quantitative results of aspect

3.3 坡型曲率

通常情况下，山体的坡型特征可以这样描述：曲率大于0的地方为凸型地貌，曲率小于0的地方为凹形地貌。然而这样简单的分类方法并不能很好的展现斜坡复杂的形态。为了更为细致的突出滑坡分布特征，本文没有采用传统的凹凸型分类，而是根据坡型曲率将研究区分为了六类：[≤-1.3]、[-1.3，-0.56]、[-0.56，0]、[0，0.45]、[0.45，1.2]、[≥1.2]。图4为坡型曲率分布统计及其量化图。

图4 坡型统计量化结果Fig.4 Statistics and quantitative results of slope type

3.4 水系

宁南县沟谷地貌发育，受河流冲刷影响，河流两岸斜坡风化侵蚀严重。由统计数据可知，在研究区域内，河流缓冲距离在300～600 m之间的量化值最大。量化的整体趋势可描述为：离河道越近，发生滑坡的数量越多，相对滑坡点密度也越大。图5为水系分布统计及其量化图。

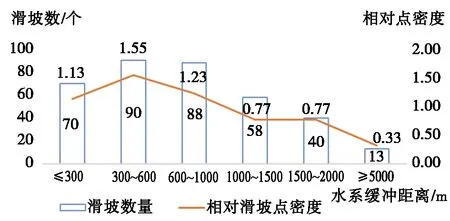
图5 水系统计量化结果Fig.5 Statistics and quantitative results of water system

3.5 岩组

根据宁南县地层分布情况，将研究区内分布的地层岩组划分为9大类，分别为：Z、Pz1、P-T、Qb-Z、T3C、J、O-S、Qal、-O。45%的滑坡点分布于P-T和J这两组地层，其中P-T类型的量化值最大，高达3.82。图6为岩组分布统计及其量化图。

图6 岩组统计量化结果Fig.6 Statistics and quantitative results of rock group

3.6 土地利用覆盖

根据国际分类标准，宁南县范围内的土地利用覆盖可分为耕地、森林、草原、灌木丛、水、防渗透表面8个类型。其中有182个滑坡发生在耕地范围内，占据了总滑坡的51%左右，而在灌木丛和防渗水面一共只有5个滑坡灾害点。由此可见，宁南县范围内土地利用覆盖因子在滑坡的发育过程中起着重大作用。图7为土地利用覆盖分布统计及其量化图。

图7 土地利用覆盖统计量化结果Fig.7 Statistics and quantitative results of land use cover

3.7 断层

断层是构造运动中最为广泛的形态之一。地区的地形地貌以及岩层的连续性通常和断层的发育有着极强的联系[18]。根据宁南县1∶25万地质图和野外调查结果显示，滑坡发育的地带通常距断层较近，而距离断层较远的区域很少发生滑坡。本文通过统计分析，将断层因子分为了七大类，分别为:[≤500 m]、[ 500 m，1 000 m]、[ 1 000 m，1 500 m]、[ 1 500 m，2 000 m]、[ 2 000 m，2 500 m]、[ 2 500 m-3 000 m]、[ ≥3 000 m]。图8为断层分布统计及其量化图。

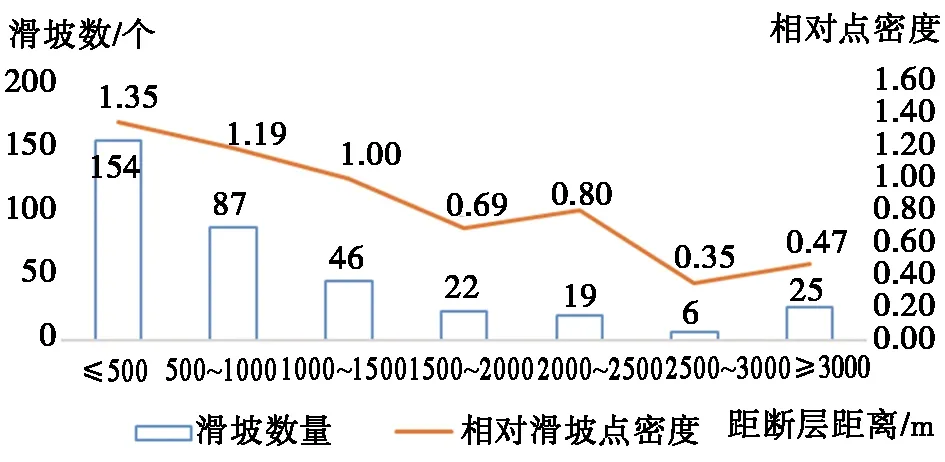
图8 断层统计量化结果Fig.8 Statistics and quantitative results of fault

3.8 高程

宁南县地貌复杂，地形起伏大，最低海拔526 m，最高海拔3 869 m。统计显示，有119个滑坡位于海拔1 094 m到1 466 m范围之间，在海拔大于2 570 m后基本没有滑坡历史点。基于此，利用自然断点法将高程分为了7大类，分别为：[526 m，1 094 m]、[1 094 m，1 466 m]、[1 466 m，1 824 m]、[1 824 m，2 190 m]、[2 190 m，2 572 m]、[2 572 m，2 987 m]、[2 987 m，3 869 m]。图9为高程分布统计及其量化图。

图9 高程统计量化结果Fig.9 Statistics and quantitative results of elevation

4 研究区易发性评价

4.1 因子相关性和权值计算

4.1.1 因子相关性计算

考虑到因子之间可能存在的相关性会使结果产生偏差，实验对量化的因子进行了相关性分析，结果表明8个因子之间的相关性都小于0.33，因子之间没有较强的相关性。计算结果中断层因子和坡型因子的相关性为0，但却没有通过显著性检验，其余因子均通过了5%的显著性检验。实验目的是想证明因子之间没有相关性，因此，可以利用所选的8个因子进行滑坡易发性评价。详细内容见表2。

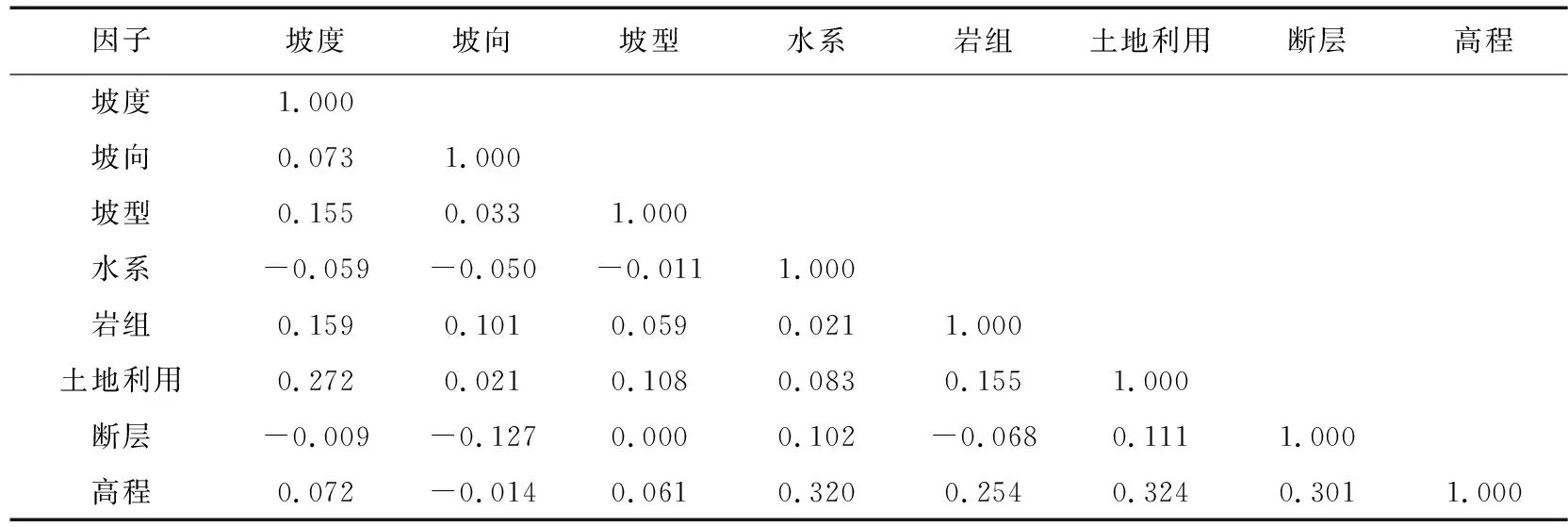
表2 因子相关性分析Table 2 Factor correlation analysis

4.1.2 熵权法计算权重

在计算因子权重之前，先将各因子的二级属性标准化，标准化计算方法见式(9)。

(9)

将标准化后的相对滑坡点密度看作概率P(x)，利用式(3)计算每个因子的信息熵。例如，坡度的信息熵值计算方法见式(10)。

(10)

最后计算得出坡度、坡向、坡型、水系、岩组、土地利用、断层、高程的信息熵分别为0.814 3、0.929 8、0.869 2、0.949 3、0.861 0、0.788 3、0.956 0、0.770 8。

再利用计算的信息熵代入式(4)，计算得出每个因子的权值，结果见表3。

表3 因子统计计算结果Table 3 Calculation results of factor statistics

从计算结果中我们可以分析得出，在南江县范围内，高程和土地利用类型对滑坡的影响程度最大，而断层的影响相对较小。

4.2 模糊综合评价

4.2.1 反距离权重法计算隶属度

由于滑坡发育的复杂性，传统的隶属函数不能凸显滑坡因子属性在各易发性级别的隶属度，基于此，本文将反距离权重法的思想用于模糊隶属度的计算。

以坡度因子为例，具体步骤如下：

(1)利用量化模型给坡度二级属性赋值，其中[0，5°]、[ 5°，15°]、[ 15°，25°]、[ 25°，35°]、[ 35°，45°]、[ ≥45°]的属性值分别为0.981 930 058、1.615 744 912、1.396 320 587、0.638 616 124、0.232 246 663、0。

(2)从量化模型的函数表达式得知，量化的值越大，发生滑坡的概率也越大。量化结果显示坡度在[ 5°，15°]这一范围内的量化值最大，从而推断出[ 5°，15°]这一范围属于高易发区的隶属度也最大。在坡度[ ≥45°]这一范围内量化的属性值为0，相应的这一范围内发生滑坡的概率小，属于不易发区的概率也就大。本文将易发区分为了五大类，分别为不易发、低易发、中易发、高易发、和极高易发。由于属性值1.616是坡度中最大的量化值，则选取该值作为极高易发区的一个基准，量化值离1.616越近，隶属高易发区的值也越大，离1.615 7越远，隶属高易发区的值也就越小。计算方法见式(11)。

ri5=1-|xi-1.616|.

(11)

其中xi为滑坡二级因子的量化值，ri5为xi所对应的二级因子隶属极高易发区的隶属度。

同理，针对另外4个易发分区，根据量化值大小选取相应的基准。坡度上，本文选择了0.232、0.639、0.982、1.396、1.616分别作为不易发、低易发、中易发、高易发、和极高易发的基准。相应的隶属结果如表4。

表4 坡度隶属度计算结果Table 4 Calculation results of slope membership

从表中我们可以得出，量化值越大的属性，对应的栅格隶属于高易发的可能性越大；量化值偏小的属性，对应的栅格隶属于低易发的可能性越大。以上信息说明该方法符合滑坡易发的基本情况，且利用反距离权重法能够很好的过度各属性在各分区上的隶属值，避免了人为干涉对数据造成的影响，同时也保留了数据本身的离散度等基本信息。实验证明，该方法能够更科学、更客观的对研究区进行易发区分区制图。值得注意的是，由于某些因子在量化时最大值和最小值差距太大(岩层因子)，导致在使用反距离权重法赋隶属度时出现不合理的情况，基于此，实验选择将这些异变的隶属度根据实际情况进行了微调，从而使计算的结果更加符合实际情况。表5为具体的计算结果。

表5 各因子隶属度计算结果Table 5 Calculation results of membership degree of each factor

4.2.2 模糊评价分区结果

通过上述步骤获取了权重矩阵W和模糊矩阵R，再由式(12)计算评价集结果。

Z=(z1,z2,z3,z4,z5)=W1×8⊙R8×5.

(12)

对于每一个栅格，通过式(12)计算后会获取5个值，取其最大值所对应的评价分区作为最终结果，计算方法见式(13)。

b=max(z1,z2,z3,z4,z5).

(13)

利用arcgis平台，本文将研究区的栅格分别赋值为1、2、3、4、5表示对应的不易发、低易发、中易发、高易发、和极高易发区域，结果如图10。

图10 宁南县滑坡易发分区图Fig.10 Zoning map of landslide susceptibility in Ningnan County

将所得分区图与滑坡历史点位图层进行叠加分析，结果显示落在不易发、低易发、中易发、高易发和极高易发的滑坡点个数分别为2、18、22、144、173。采用相对滑坡比来验证模型可行性。计算方法见式(14)。

(14)

其中ni为易发性分区i下的滑坡个数；si为易发性分区i的栅格个数；N为研究区总滑坡个数；S为研究区总栅格数。结果如表6。

表6 分区统计结果Table 6 District statistics results

5 结论

(1) 将各因子的统计特征量化为相对滑坡点密度，以此为基础，使用熵权法计算获得了各评价因子的权值，结果显示高程和土地利用是研究区主要的滑坡易发性影响因子。

(2) 将反距离权重法的思想用于模糊隶属度的计算。实验证明该方法能够很好的过度因子二级属性在各分区上的模糊隶属值，同时能够更科学，精确的对研究区进行易发性分区制图。

(3) 宁南县滑坡易发性分区图中，从不易发区到极高易发区所占的比例分别为18.7%、25.8%、11.3%、31.4%、和12.7%。其中高易发区和极高易发区多位于宁南县东南侧和黑河水系两侧。将易发性分区图与历史灾害点图层进行叠加分析，结果显示有88.3%的滑坡分布于极高易发区和高易发区，从低易发到极高易发的相对滑坡比分别为0.03、0.19、0.54、1.28和3.78。说明该模型计算结果与实际情况高度相似，反距离权重法的思想在模糊隶属度的计算上具有较高的适用性。