圆端形钢管混凝土柱的抗震性能分析

程 毅

(湖北省招标股份有限公司，武汉 430071)

圆端形钢管混凝土柱是指在截面形状为圆端形的空钢管中浇筑混凝土而制成的组合柱。由于钢管对混凝土的环向约束作用，有效限制了混凝土的侧向变形，充分发挥了混凝土的抗压性能，因此，钢管混凝土柱具有承载能力高、延性性能好、施工简便等优点，被广泛使用于桥梁工程，如琼海九曲江大桥、苏州市斜港桥以及武汉市黄陂区后湖斜拉桥的双肢桥塔等工程[1]。圆端形钢管混凝土柱相比于圆形截面而言，具有更大的横向刚度，有利于提高桥梁横桥向的刚度及稳定性；相比于矩形截面而言，对内部混凝土的约束作用更强，有利于减小水流对柱体的冲击作用。

现有研究多关注于圆端形钢管混凝土柱的静力性能，王二磊[2]对圆端形钢管混凝土短柱进行了轴压及偏压试验，结果表明圆端形钢管混凝土具有较好的竖向承载能力，而偏心率是影响圆端形钢管混凝土偏心受压性能的主要因素。李培鹏等[3]基于Python语言进行参数化建模，通过有限元分析探究了不同混凝土材料模型的适用性，分析了高宽比对圆端形钢管混凝土短柱的约束性能和承载能力的影响。李宁波等[4]对圆钢管混凝土柱进行了往复荷载下的滞回分析，将计算结果与试验结果进行对比得知两者的滞回曲线吻合较好，验证了模型的正确性。邢新等[5]对带肋薄壁方钢管混凝土柱进行了试验和有限元研究，研究表明带肋可以有限提高柱的承载力和延性，但会增大轴压比，降低钢管混凝土柱的延性和耗能能力，对抗震不利。

综上所述，现有研究较少关注圆端形钢管混凝土柱的抗震性能，主要集中于圆形或方形钢管混凝土柱，而对圆端形钢管混凝土柱滞回性能的研究鲜见报道。为此，采用ABAQUS软件对圆端形钢管混凝土柱的滞回性能进行有限元分析，研究圆端形钢管混凝土柱的滞回性能及相关参数对其的影响。

1 有限元模型的建立

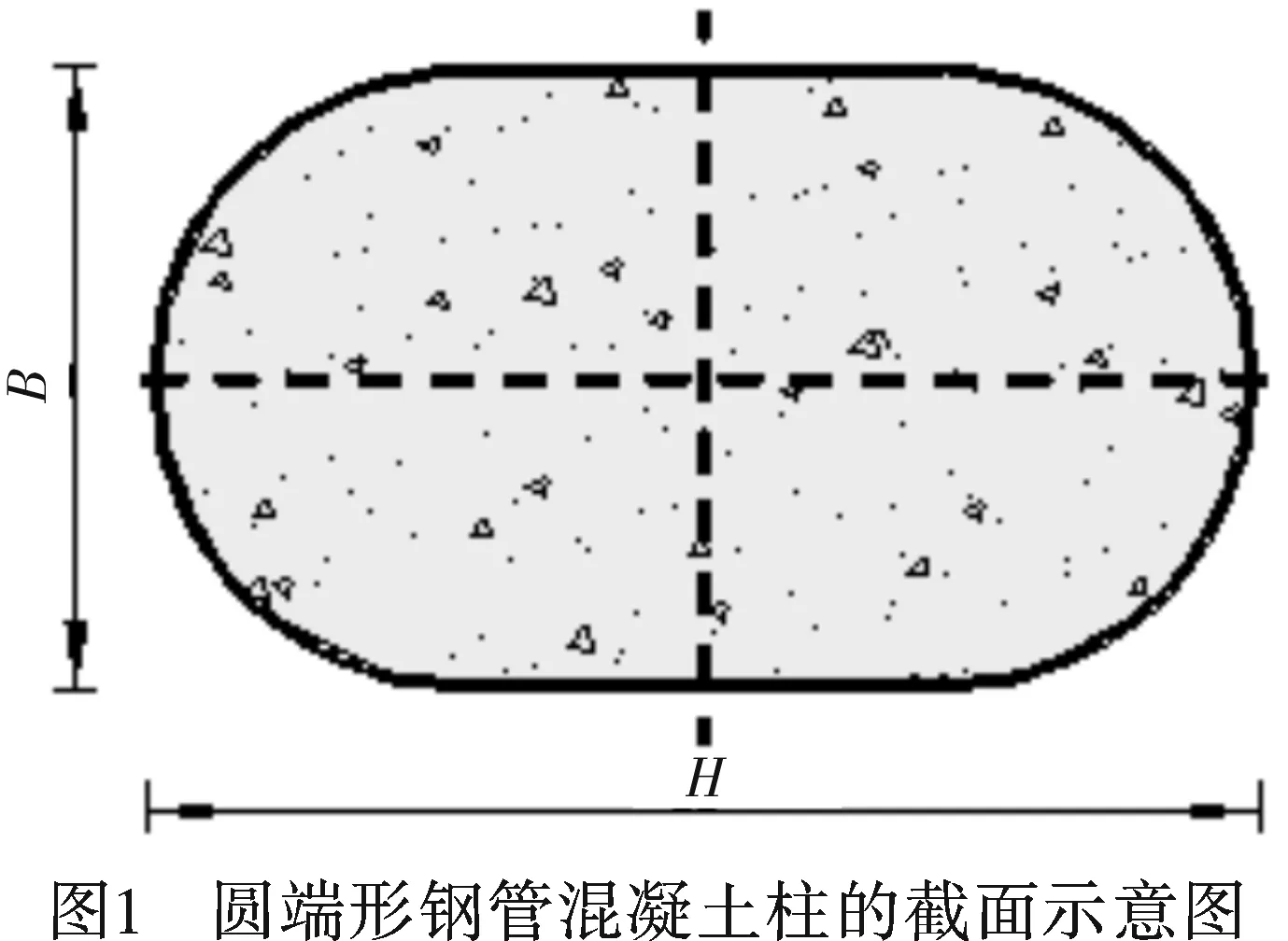
利用ABAQUS软件建立了三个轴压比不同的圆端形钢管混凝土柱的有限元模型，其截面形状如图1所示，其中B为截面宽度，H为截面长度，试件基本参数如表1所示。

表1 试件基本参数

该有限元模型采用单元一共分为两类，一类是八节点减缩积分格式的三维实体单元(C3D8R)，该类单元可用于模拟产生较大的网格扭曲，适合进行大应变分析，在此主要用于核心混凝土和上下端板的创建；第二类单元为四节点缩减积分格式的壳单元(S4R)，在此主要用于对钢管的创建。

钢材采用双线性随动强化模型，考虑包兴格效应的影响。钢材本构分为弹性阶段和强化阶段，在弹性阶段，钢材的弹性模量和泊松比分别取206 GPa和0.25，后期强化阶段的弹性模量取为弹性阶段的0.01倍[6]。混凝土采用混凝土塑性损伤模型，基于拉、压各向同性塑性的连续线性损伤模型，可较好地模拟混凝土在单轴、双轴等复杂状态下的工作性能。其中塑性参数中膨胀角取30，流动势偏量取0.1，双轴受压与单轴受压极限强度比取为1.16，不变量应力比取为0.667，混凝土的黏性系数修正为0.000 5，增加结构的刚度，提高软化阶段的收敛效率[7]。混凝土塑性损伤模型的受拉应力-应变关系采用沈聚敏[8]提出的混凝土受拉本构模型。混凝土受压本构采用韩林海[6]提出的核心混凝土本构模型计算，基于大量圆形、方矩形钢管混凝土短试件轴压试验数据，深入探究了混凝土强度和约束系数对应力-应变曲线的影响，提出了圆形和方矩形钢管混凝土中混凝土的本构关系模型。

混凝土塑性损伤模型将损伤指标引入混凝土模型，对混凝土的弹性刚度矩阵加以折减，以模拟混凝土的卸载刚度随损伤增加而降低的行为；同时通过引入刚度修复因子来模拟混凝土裂缝在受压闭合时刚度的恢复效应。受压恢复系数取0.2，受拉恢复系数取0。往复荷载下混凝土受拉损伤因子dt、受压损伤因子dc的计算分别如式(1)、式(2)所示[9]。

(1)

(2)

式中，dt和dc分别为受拉损伤因子和受压损伤因子；Ec为混凝土初始弹性模量；σt和σc分别为拉应力和压应力；εt和εc分别为拉应变和压应变；σt0和σc0分别为初始拉应力和初始压应力。

钢管与混凝土的界面模型由法向的接触和切向的黏结滑移组成，选择“硬”接触作为钢管与核心混凝土的法向接触行为。采用库仑摩擦模型来模拟钢管与核心混凝土界面切向力的传递：界面可以传递剪应力，直到剪应力达到临界值，界面之间产生相对滑动，摩擦系数μ取0.5[10]。端板与核心混凝土的接触采用Tie，其中刚度大的端板为主面，核心混凝土作为从面；端板与钢管的接触采用壳与实体耦合的形式。

圆端形钢管混凝土柱的底端采用固定约束，柱顶释放其截面横向和构件纵向的平动约束，柱顶施加轴向荷载和水平往复荷载。对水平往复荷载，采用荷载-位移联合控制方式进行加载。柱顶需施加竖向集中力，在施加荷载区域建立参考点，并将这个参考点与加载区域建立一个耦合约束，集中力施加在参考点上，ABAQUS 会自动默认为该集中力均匀的分布在加载区域；水平荷载利用 ABAQUS 中 amplitude命令进行反复加载，试件屈服前采用荷载控制并分级加载，每级荷载循环一次；试件屈服后采用位移控制，取屈服时试件位移值的0.25 倍为级差控制加载，每级荷载循环两次，直到试件破坏。

2 计算结果分析

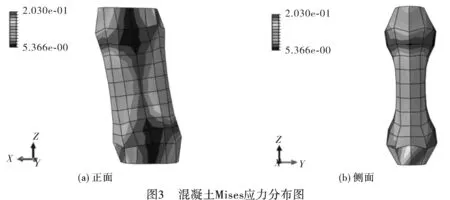
以轴压比为0.6的模型B为例，在位移加载最后一个循环时，钢管Mises应力分布云图和混凝土Mises应力分布云图分别如图2和图3所示。由图可知，钢管在上下端部Mises应力最大，且产生较大的局部屈曲变形，此时由于钢管的局部鼓曲，钢管对混凝土的约束作用也会削弱，导致混凝土在构件上下端也会产生较大的鼓曲，使端部混凝土被压碎。同时，截面平直段的变形比两侧圆弧段严重，表明钢管平直段对混凝土的约束效应弱于圆弧段对混凝土的约束效应，所以在圆端形钢管混凝土柱的设计方面要引起注意。

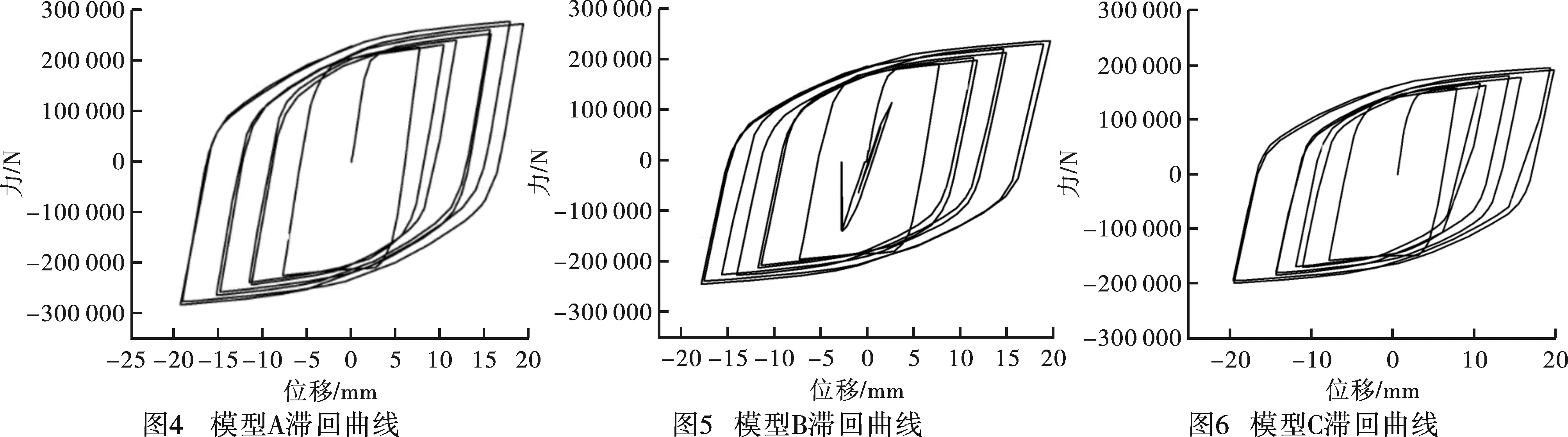
通过控制变量方法研究轴压比对圆端形钢管混凝土柱抗震性能的影响，图4、图5、图6分别表示轴压比为0.4、0.6、0.8的圆端形钢管混凝土柱在横向水平荷载作用下荷载作用点处的水平力-位移滞回曲线。由图可知，随着轴压比的增大圆端形钢管混凝土柱的侧向刚度在减小，抗震性能随之变差。

3 结 语

圆端形钢管混凝土柱在往复荷载下破坏主要发生在构件的上下端部，此处钢管和核心混凝土会产生严重的鼓曲破坏，钢管局部屈曲，混凝土被压碎。截面平直段的鼓曲变形比圆弧段更加严重，表明了圆形钢管比矩形钢管对于核心混凝土的约束作用更强。通过荷载-位移滞回曲线可知轴压比会降低圆端形钢管混凝土柱的横向刚度，减小水平承载力，对于抗震耗能起着不利作用。