超簇加权的集成聚类算法
薛红艳,钱雪忠,周世兵
江南大学 人工智能与计算机学院,江苏 无锡 214122
集成聚类通过对基聚类实施组合策略以得到更好的结果,在发现奇异聚类、处理噪声和集成来自多个分布式源的聚类上具有较好的优势[1]。现有集成聚类算法的研究主要集中在两方面:一是如何生成性能好且有差异性的基聚类[2-5];二是如何设计一致性函数,如共协矩阵[6-9]、图分割[8]等方法得到集成聚类结果。
目前,大多数集成聚类算法仍存在三个局限性。第一,由于K-means 算法实现简单,计算复杂度不高且执行速度快,故大多集成聚类算法均使用Kmeans 方法生成基聚类[8-9]。但对于结构复杂尤其是边界不易区分、非球形分布或高维数据的数据集,使用K-means 算法无法产生较好的聚类结果,而质量较低的基聚类会影响共协矩阵的聚类结构,降低集成聚类的性能[8,10-11]。第二,大多数集成聚类算法忽视了基聚类多样性的不同,平等地对待每个基聚类[12]。第三,现有的集成聚类算法通常将数据对象作为生成共协矩阵的基本操作单元[8,11-12],当样本数目或集成规模较大时,计算负担明显增加。针对该问题,有研究者提出以相交簇作为操作单元[13-14]来降低算法的复杂度,但随着集成规模的增长,相交簇的数目显著增加,复杂度随之增加。
鉴于以上三个问题,本文提出了超簇加权的集成聚类算法(ensemble clustering algorithm based on weighted super cluster,ECWSC)。该算法首先提出一种新的生成基聚类的算法,即基于地标点的谱聚类算法。在对数据集使用基于地标点的谱聚类算法得到基聚类后,以信息熵为依据计算基聚类的不确定性,赋予基聚类相应的权重,并使用加权的方式得到基于超簇的共协矩阵。最后对共协矩阵使用层次聚类[4]算法进行聚类,得到最终结果。
1 基本技术
1.1 聚类集成
聚类集成主要分为两个步骤:生成基聚类和集成基聚类。假设数据集X={x1,x2,…,xN}是包含N个数据对象的样本集,对X执行M次聚类算法得到M个基聚类,将其标记为基聚类集合Π={π1,π2,…,πM}。其中,表示第m个基聚类,表示πm中第i个类簇,nm表示πm中类簇的总数。以为例,n1表示对数据集X执行一次聚类算法所得类簇的数目,是基聚类π1中的第一个类簇。将基聚类集合Π中所有的类簇用集合C={C1,C2,…,Cnc} 表示,则nc=n1+n2+…+nM,Ci是基聚类集合中的第i个类簇。若Cj∈πm且xi∈Cj,则Clsm(xi)=Cj。
集成基聚类的方法有共协矩阵[6-9]、图分割[8]等方法。本文主要使用共协矩阵进行集成。
1.2 基于相交簇的共协矩阵组合策略
得到基聚类集合后,大多集成聚类算法通过计算两两样本出现在同一个类簇中的次数,得到基于样本的共协矩阵[15-17]。但随着样本数目的增加,算法的复杂度显著提升。
为改进上述问题,有学者提出使用相交簇作为操作单元[13-14]。相交簇集合IO={IO1,IO2,…,IONˉ}是类簇相交的集合,IOi表示相交簇集合中第i个相交簇,Nˉ表示在基聚类集合中相交簇的总数。相交簇两两互不相交,且相交簇的集合即为样本的集合。∀xi,xj∈IO,∀πm∈Π,Clsm(xi)=Clsm(xj)且∀xi∈IO,xj∉IO,∃πm∈Π,Clsm(xi)≠Clsm(xj)。如图1 所示,样本x1与x2在3 个基聚类中均聚类到一个簇中,故Clsm(x1)=Clsm(x2)。基于相交簇的共协矩阵可表示为:

其中,Aij表示相交簇IOi和相交簇IOj出现在同一类簇中的次数与集成规模M的比值。若相交簇IOi与相交簇IOj在第m个基聚类中聚类在同一个类簇中,则=1,否则=0。
如图1(a)~(c)所示,基聚类集合Π由3 个基聚类组成,分别为π1、π2和π3。其中基聚类π1、π2均有4 个类簇,π3有3 个类簇,通过对基聚类叠加处理,生成了图1(e)所示的7 个相交簇,在以簇为操作单元的共协矩阵中,元素A13=2/3。
1.3 超簇
超簇[18]是使用碎片整理策略对相交簇处理后得到的类簇。在相交簇集合IO的基础上,先定义阈值λ(λ>0)判断类簇IOi是否为碎片对象,若IOi中数据样本的数目低于λ,则称IOi为碎片对象,需要对其使用碎片整理策略进行碎片整理。碎片整理策略是通过计算相交簇与相交簇之间的相似度,迭代地将每个碎片对象合并到与之相似度最高的类簇中,从而得到超簇集合。相交簇IOi与IOj之间的相似度计算如下:

Fig.1 Demo of generating super cluster图1 超簇生成的演示
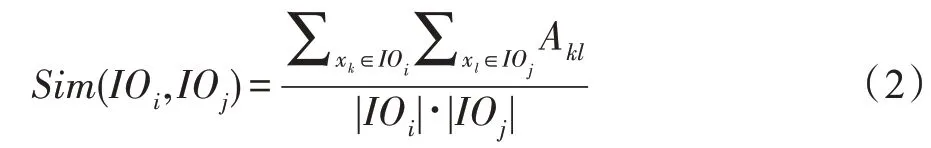
其中,Akl=,nkl表示xk和xl在M次基聚类中出现在同一个簇的次数。如图1(f),当λ=1 时,使用碎片整理策略对相交簇进行整理,得到5 个超簇。
1.4 相关工作对比
大多数集成聚类算法使用K-means 算法生成基聚类[8-9],但用K-means 算法生成的基聚类效果不太理想。针对该问题,本文提出基于地标点的谱聚类算法生成基聚类。该算法先从数据集中随机选取部分候选点,对候选点使用谱聚类算法得到候选点的聚类结果,最后将样本点映射到最近邻地表点上,得到最终的基聚类结果,使用该方法可以提高基聚类的质量。
对生成的基聚类进行集成时,集成聚类算法通常以样本作为操作单元[15-17]得到共协矩阵,当样本数目较多时,算法的复杂度显著提高。针对该问题,有研究者提出使用相交簇[13-14]来降低共协矩阵的规模,但相交簇的数目会随着集成规模的增长而显著增加,共协矩阵规模仍较高。为解决上述问题,本文使用超簇作为操作单元,并根据基聚类的不确定性对基聚类赋予对应的权重,得到基于超簇加权的共协矩阵。至此,超簇加权的集成聚类算法得以提出。
2 超簇加权的集成聚类算法
针对大多数集成聚类算法使用聚类效果较差的K-means 算法生成基聚类,使用共协矩阵对基聚类进行集成时,忽略了基聚类多样性的不同,平等地对待基聚类,且以样本为操作单元生成共协矩阵,导致算法效果差,复杂度高。本章对所提超簇加权的集成聚类算法进行详细介绍。
2.1 基于地标点采样的谱聚类算法
当前,很多集成聚类算法使用K-means 算法生成基聚类,但该算法在初始化聚类中心时易受初始值的影响。虽然谱聚类算法的准确度比较高,但也具有较高的时间和空间复杂度。文献[19-23]均采用候选点或类似方法来提升谱聚类算法的扩展性,但在复杂度或准确率方面表现欠佳。本节提出使用随机与K-means 结合的方法选取地标点,再对地标点使用谱聚类算法得到其聚类结果,通过将样本映射到与之最近邻的地标点上得到基聚类的结果。
地标点的选取方法如下:先从包含N个样本的数据集中选出P′个候选点。由于较大的非球形簇可以视为由多个较小的球形簇构成,且K-means 算法在球形簇上表现佳、速度快,故对P′个候选点使用Kmeans 方法得到P个地标点。地标点是对候选点使用K-means 算法得到的K个中心点,其稀疏线性组合可视为原始数据集。如图2 所示,从图(a)所示的数据集中随机选取P′个候选点得到图(b),再对图(b)中的候选点使用K-means 聚类方法,得到P个地标点。
从数据集中随机选取P′个候选点时,较大的P′通常会包含较多类别的样本,但增加了选取地标点的复杂度。P′太小,则无法包含所有类别的样本,对基聚类的质量会有一定的影响。但单个基聚类的质量对集成聚类的结果有引导但不起决定作用。为降低随机选点对基聚类质量的影响,在集成基聚类时,若单个基聚类的质量较低,对应的权重会有相应的变化。此外,在对相交簇使用碎片整理策略生成超簇,构建共协矩阵时,会进一步对不稳定的碎片对象进行处理,故对集成聚类的结果不会产生较大的影响。
地标点的聚类结果对数据集中样本点的聚类结果有引导作用。在得到地标点的聚类结果后,通过将样本映射到与之最近邻的地标点上可得到基聚类的结果。由于谱聚类算法的复杂度与样本数目呈正相关,但对数据分布的适应性更强,选出地标点后,聚类的样本数目降低,且地标点比小簇中候选点的分布更复杂,故对地标点采用谱聚类算法可以间接提高基聚类的质量。
在得到P个地标点的聚类结果后,将所有的样本点映射到与之距离最近的地标点上,可以得到全部样本点的聚类结果,即基聚类的聚类结果。一些学者提出通过计算N个样本点与P个地标点之间的距离,来获得距离样本点最近的地标点[19-23]。为降低算法的时间和空间复杂度,本文提出通过计算样本点与之最近邻地标点簇的方式来获得与样本点距离最近的地标点。
如图3 所示,首先使用K-means 方法对图(a)中的地标点进行一次聚类,得到7 个地标点类簇。然后计算样本点xi与每个地标点簇中心的距离,选择与样本点最近邻的地标点簇,如图(d)所示。再分别计算样本点与最近邻地标点簇中地标点之间的距离,从中选择与样本点距离最近的地标点,如图(f)所示。将数据集中所有的样本点映射到与其最近的地标点上,最终可得到基聚类的聚类结果。
2.2 基于类簇不确定性的权重分配
得到基聚类成员后,有部分集成聚类算法根据聚类指标值从基聚类集合中筛选出质量较高的基聚类成员进行集成聚类[24]。使用指标值对基聚类筛选,增加了算法的计算负担。针对上述问题,本文提出用类簇的不确定性来衡量基聚类的质量,对基聚类赋予相应的权重。
为评估每个基聚类的不确定性,先计算基聚类中类簇的不确定性。在基聚类集合Π中,类簇Cm i相对于基聚类集合Π的不确定性为:

Fig.2 Selection of landmark points图2 地标点的选取

Fig.3 Nearest landmark point of sample point图3 样本点的最近邻地标点

用基聚类的平均熵表示基聚类不确定性,给定基聚类集合Π,基聚类成员πm的不确定性为:

其中,nm表示基聚类πm中类簇的数目。

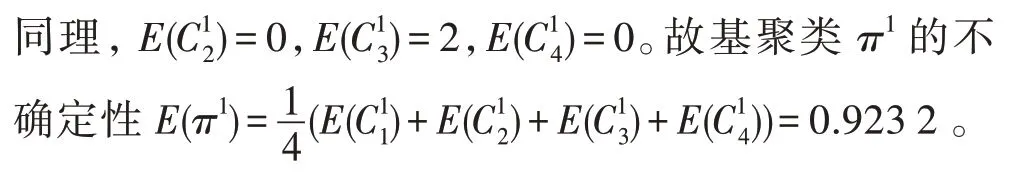
有研究者发现,效果更好而多样性低的基聚类集成效果低于多样性高的基聚类集合[24]。基聚类的不确定性越高,则该基聚类所包含的信息量越大。为更好地满足基聚类好而不同的要求,对该基聚类赋予更高的权重。通过对基聚类的不确定性进行归一化处理得到相应的权重,权重范围为[0,1]。至此,基聚类πm的权重W(πm)可表示如下:

2.3 基于权重超簇的共协矩阵
大多集成聚类算法使用共协矩阵得到样本之间的相似度时,平等地对待每个基聚类[3-4],忽略了基聚类多样性的不同。鉴于此,一些学者对该方法进行了改进,例如使用样本加权策略[25]来改进共协矩阵。为降低以样本或相交簇为操作单元计算共协矩阵带来的计算负担,本文以超簇为操作单元并引入权重的策略。将基聚类生成相交簇后使用碎片整理策略得到的超簇标记为Z={z1,z2,…,zN*},N*表示超簇的数目。则基于加权超簇的共协矩阵WECA可表示如下:

2.4 超簇加权的集成聚类算法步骤
超簇加权的集成聚类算法流程简单描述如下:
输入:数据集X,候选点数P′,地标点的个数P(N>>P′>>P),聚类数K,碎片对象的阈值λ,基聚类的数目M。
输出:集成聚类结果C。
步骤1从数据集X中选取P′个候选点,使用Kmeans 的方法将P′个候选点聚类成P个簇,P个簇的中心点即为地标点。
步骤2将数据集中的每个样本点分配到与其点距离最近的地标点。
步骤3对P个地标点使用谱聚类的方法,生成K个簇,得到P个地标点的聚类结果。
步骤4将数据集中的样本点映射到地标点上,得到全部样本点的聚类结果。
步骤5重复M次步骤1、2、3 和4,得到基聚类集合Π。
步骤6根据式(4)和式(5)计算基聚类的权重W。
步骤7根据式(2)对步骤5 中生成的相交簇使用碎片化策略处理,得到超簇Z。
步骤8根据式(6)以超簇Z为操作单元,W为基聚类权重,生成WECA矩阵。
步骤9在WECA矩阵上执行层次聚类算法[26]得到最终结果C。
3 实验验证
为验证超簇加权的集成聚类算法的有效性和优良性能,本章从人工数据集和真实数据集两方面对所提集成算法进行验证,本文实验的环境为Intel Core i7-8565U CPU@1.80 GHz 1.99 GHz,Windows10,Matlab2019a等。
3.1 基于人造数据集的验证
本节在表1 所示的4 组人造数据集上进行实验验证。Smile2 数据集是由2 个团状簇、1 个环状簇和1个流行簇组成,2d-4c-2 数据集由4 个团状簇组成,Dartboard1 数据集由4 个环状簇组成,Banana 数据集则是由2 个流行簇组成。概率轨迹累积(probability trajectory accumulation,PTA)算法[14]是基于相交簇的集成聚类算法,本节使用PTA 算法与所提ECWSC 算法进行对比。

Table 1 Artificial datasets表1 人工数据集
为保证实验的公平,图4 和图5 中集成规模M的值均设置为10,均采用不同的颜色来区分聚类的结果,同一类簇中的样本用同一颜色表示。在PTA 与ECWSC 算法中,数据集Smile2、2d-4c-2 和Dartboard1的类簇数目均设置为4,Banana 数据集的类簇数目设置为2。图5 中红色的点表示集成规模M为10 时,使用ECWSC 算法生成第10 个基聚类成员时选择的地标点。数据集Smile2、2d-4c-2 和Banana 地标点的数目均设置为300,Dartboard1 地标点的数目设置为600。
从图4 可见,PTA 算法在4 个人工数据集上均无法得到正确的聚类结果。图5 中,ECWSC 算法将Smile2、2d-4c-2、Dartboard1 数据集聚为4类,将Banana数据集聚为2 类,且都得到了正确的聚类结果。
3.2 基于真实数据集的验证
为进一步验证ECWSC 算法的性能,本节将ECWSC 算法在表2中的7个真实数据集上,与6 种实验方法进行对比。对比实验分别为PTA、概率轨迹图划分(probability trajectory based graph partitioning,PTGP)[14]、局部加权证据累积(locally weighted evidence accumulation,LWEA)[9]、局部加权图划分(locally weighted graph partitioning,LWGP)[9]、传播聚类相似性(propagating cluster-wise similarities,ECPCS-HC)[15]、证据累积聚类(evidence accumulation clustering,EAC)[6]。
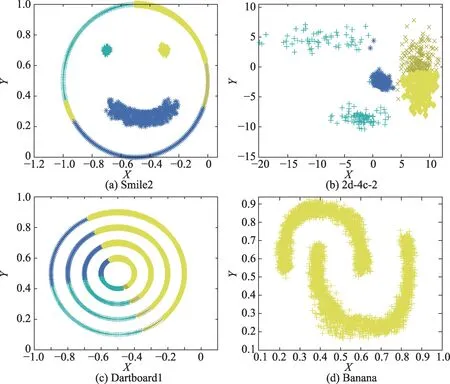
Fig.4 Clustering result of PTA on artificial datasets图4 PTA 算法在人工数据集聚类表现
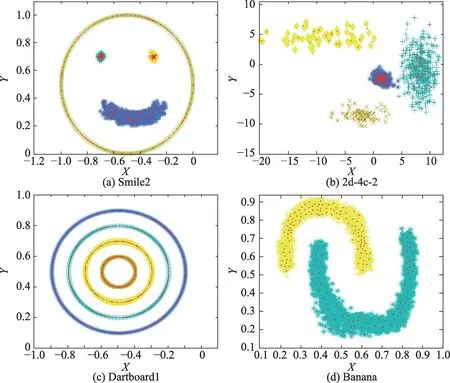
Fig.5 Clustering result of ECWSC on artificial datasets图5 ECWSC 算法在人工数据集聚类表现
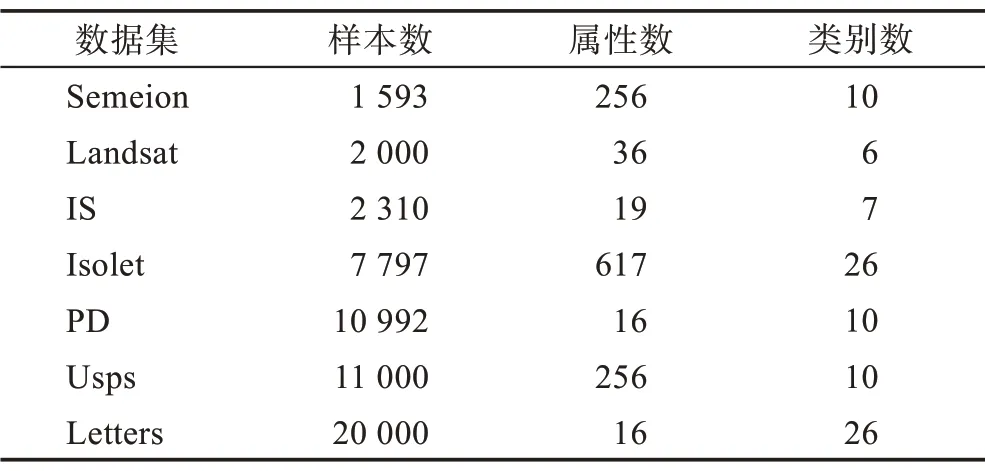
Table 2 Real datasets表2 真实数据集
真实数据集分别是Semeion、Landsat、IS(image segmentation)、Isolet、PD(pen digit)、Usps、Letters。其中,Letters、Usps 数据集来自文献[5],其他来自UCI数据集,数据集的详细信息可见表2。
实验采用标准化互信息(normalized mutual information,NMI)和调整兰德系数(adjusted Rand index,ARI)两个指标对聚类结果进行评价。NMI 从信息论的角度评估两个类之间的相似性,取值范围为[0,1],ARI 指标则可以衡量两个数据分布的吻合程度,取值范围为[-1,1]。二者的结果均为越接近1,效果越好。
当P过大时,对地标点使用谱聚类算法会增加生成基聚类的复杂度,P过小时,地标点将无法包含所有类别的样本。当数据集的样本非常多或非常少时,可以适当地减少或者增加P值的设置,为保证实验的公平,且考虑到本文的数据集样本数均在103~105之间,故本实验在使用基于地标点采样的谱聚类算法生成基聚类时,地标点参数P设置为1 000。为减少参数的设置,随机候选点的数目P′=10P,当P′的值超出数据集的样本数时,P′默认设置为样本数的大小。碎片对象λ的阈值大小参照文献[18]的设置,阈值的大小为5。6 个对比实验均使用随机Kmeans 算法生成基聚类,其范围为[1,K],聚类数目K值的大小与数据集的类别数目一致,集成规模的尺寸M=20。实验结果如表3 所示,表中数据是运行20次所得结果的平均值和标准差,均采用百分数的形式表示,表中每个数据集对应效果最好的两个算法的数据均已加粗显示。
相比于将样本视为操作单元的LWEA、LWGP、EAC 算法和将相交簇视为操作单元PTA、PTGP、HC算法,ECWSC 算法将随机选点与K-means 选点的方法相结合来选取地标点,并使用基于地标点的谱聚类算法生成基聚类。在此基础上,使用信息熵的方法计算基聚类中类簇的不确定性,并赋予基聚类相应的权重,再使用加权的方式得到基于超簇的共协矩阵。从实验结果可知,ECWSC 在多个数据集上的标准方差低于对比实验,这表明相比于对比算法,ECWSC 算法的稳定性较好。
从表3 的实验结果可见,在Letters 数据集上,LWEA 与LWGP 算法在对样本实施加权策略时,算法运行超出内存无法得到聚类结果,故将其指标值用“N/A”标记。与使用样本为操作单元相比,ECWSC算法使用了超簇作为操作单元,在构建共协矩阵时,复杂度显著降低,故仍可以运行出较好的结果。这表明ECWSC 算法在空间复杂度上占据了一定的优势。此外,从数据集在算法上的表现可知,ECWSC算法相比于其他几个对比实验,在NMI 和ARI 指标上值均有显著提升。其中,ECWSC 算法相比于对比实验,NMI 的值提高了5%~25%,ARI 的值则提高了3%~25%。提升最为显著的是Usps 数据集,其NMI指标值提高了24.25%,ARI 指标值提升了24.14%,这表明使用超簇加权的集成聚类算法相比于其他算法在准确度上有一定的优势。
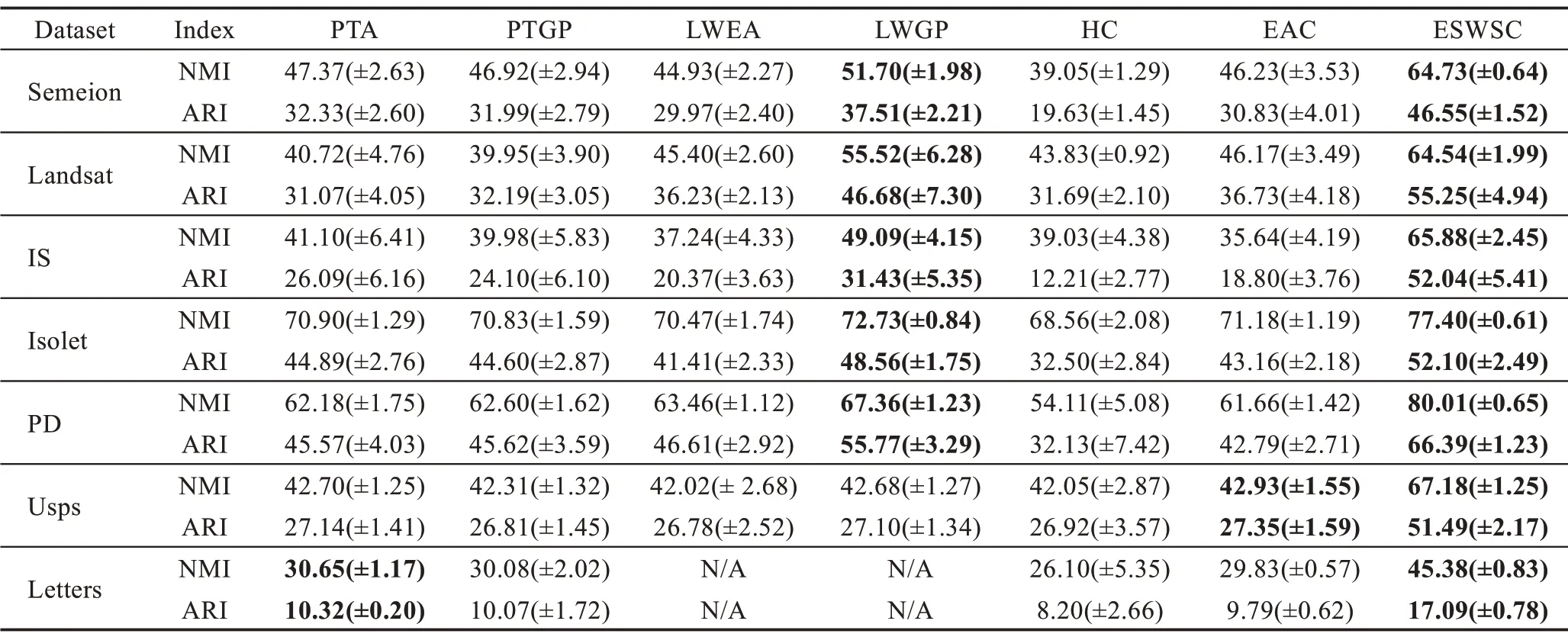
Table 3 Performance of different algorithms on datasets(M=20)表3 不同算法在数据集上的表现(M=20)%
为验证ECWSC 算法在时间复杂度上相比于其他算法有所改进,将上述的7 个算法在表2 所示7 个数据集上运行的时间进行对比。集成规模M为20时,执行20 次算法所用时间的平均值作为运行该算法所用时间,实验结果如图6 所示。图中的横坐标表示不同的集成聚类算法,纵坐标表示该算法在当前数据集上运行的时间。在柱状图中,同一数据集在不同算法上运行的时间使用同一个颜色的矩形表示。由于LWEA 算法和LWGP 算法在Letters 数据集上运行超出内存,无法得到聚类结果,故其运行时间未在图中标记。
将数据集在7 个算法上运行的时间进行分析。以Semeion 在7 个算法上运行时间为例,ECWSC 算法在Semeion 数据集上的平均运行时间是0.01 s,6 个对比实验中,平均运行时间最低的算法为LWGP 算法,运行时间为1.2 s,其运行效率远低于本文算法。从图6 可见,当样本数目较多时,本文算法的运行时间远低于其他6 个对比实验。此外,当Letters 数据集在对比实验上运行超出内存而无法得到聚类结果时,本文算法依旧可以得到较好的聚类效果。当数据集中样本数目增长时,6 个对比算法的运行时间会显著提高,但ECWSC 算法的运行时间增长仍比较缓慢。
从7 个算法在真实数据集上运行的时间和算法准确度的表现可知,本文所提的ECWSC 算法在生成基聚类时,采用基于地标点的谱聚类算法降低了生成基聚类的复杂度。在集成基聚类时,使用超簇作为操作单元且对基聚类赋予相应的权重,降低了共协矩阵的规模。相比于其他算法,上述方式均降低了算法的复杂度,在运行时间上有一定的优势。
4 集成规模与集成结果
本章评估ECWSC 算法与其他集成聚类算法在不同集成规模M下的表现,以获取集成规模M与集成聚类结果之间的关系,从表2 中选取4 个真实数据集,分别是Semeion、IS、Isolet、PD 数据集进行实验。其中,对比实验仍选取以样本为操作单元的LWEA、LWGP、EAC 算法和以相交簇为操作单元的PTA、PTGP、HC 算法。算法集成规模M的值均由10 增长为50,步长设置为10。与上章实验一致,ECWSC 算法地标点参数P设置为1 000,随机候选点的数目P′=10P,碎片对象λ大小为5。
为降低实验结果的偶然性,所有的实验值均采用运行20 次所求NMI、ARI 的平均值。其中,图7 和图8 中的横坐标均表示集成规模的变化,图7 中的纵坐标表示算法结果NMI 的值随集成规模M的变化。图8 中的纵坐标表示算法结果ARI 的值随集成规模M的变化,其中红色的线表示超簇加权的ECWSC 算法集成聚类结果。
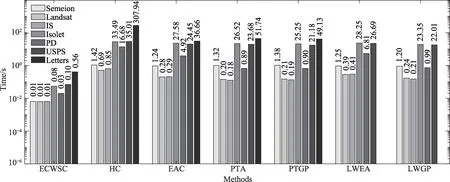
Fig.6 Time cost of 7 methods on different datasets图6 不同数据集上7 种算法的时间成本

Fig.7 NMI values for different methods under different M图7 不同集成方法在不同M 下的NMI值

Fig.8 ARI values for different methods under different M图8 不同集成方法在不同M 下的ARI值
从图7 和图8 的实验结果可见,对于同一集成规模M,无论是NMI 或是ARI 的比较,ECWSC 算法在Semeion、IS、Isolet、PD 数据集上的运行效果均高于几个对比实验,其NMI 和ARI 的值相比于对比实验提高0.05~0.30。从图7 和图8 可见,随着集成规模M的变化,对比实验的结果均有较为显著的提高或降低,而ECWSC 算法的运行效果仍较稳定。
5 结束语
本文提出了超簇加权的集成聚类算法。该算法提出基于地标点的谱聚类算法生成基聚类,在此基础上计算基聚类的不确定性,赋予基聚类相应权重,并使用加权的方式得到基于超簇的共协矩阵,最后使用层次聚类算法对超簇进行聚类。通过多组对比实验证明超簇加权的集成聚类方法能够有效提升聚类集成的聚类效果。在后续的工作中会进一步考虑自动确定聚类数目,并将所提聚类算法用于实际应用中,如将图像分割技术与本文算法相结合。

