融合区域与朋友影响的下一兴趣点推荐

张奥雅，石美惠，申德荣，寇 月，聂铁铮

东北大学 计算机科学与工程学院，沈阳 110819

随着基于位置的社交网络（location-based social network，LBSN）如Foursquare、Gowalla 的流行，用户可以利用手机等移动设备来搜索兴趣点，并在社交平台上发布其签到的兴趣点，与朋友分享该兴趣点的体验与感受。大量的签到兴趣点信息收集在LBSN 中，兴趣点推荐是利用这些签到信息，根据用户历史的移动行为来预测用户的偏好，并向其推荐一组未访问的兴趣点。

近年来，兴趣点推荐越来越受到人们的关注，而下一兴趣点推荐成为兴趣点推荐的一个新的研究热点。下一兴趣点推荐是根据用户历史访问的兴趣点，同时结合用户当前所访问的兴趣点信息，向用户推荐下一时刻可能访问的兴趣点。与传统的兴趣点推荐不同，下一兴趣点推荐考虑了用户签到兴趣点的连续性以及用户签到兴趣点之间的时序关系。一些较为成熟的下一兴趣点推荐模型，如基于协同过滤的推荐模型[1]和基于马尔可夫链的推荐模型[2]，只能捕获相邻兴趣点之间的关系，使推荐的兴趣点只与最近签到的兴趣点有关，忽略了用户与兴趣点的集体依赖。目前较为流行的基于深度学习的下一兴趣点推荐模型[3-4]，考虑的影响因素比较单一，例如文献[3]仅对时间演化进行建模，文献[4]采用GRU（gated recurrent unit）模型，只考虑了时间、空间上的连续性。针对下一兴趣点推荐已有很多研究成果，但仍然难以取得满意的推荐性能。

用户在不同时间签到的兴趣点是不断变化的，最近的一些研究尝试利用影响用户签入的信息来提高推荐的准确性。虽然用户在连续时间内更倾向于访问距离较近的兴趣点，但并不是相邻的兴趣点之间的距离越近越好，如用户在不同时间跨区域访问兴趣点。因此，需要捕获某时刻兴趣点的粗粒度信息，将某一时刻的区域信息嵌入到兴趣点中能更加准确地为用户推荐下一兴趣点。例如，随着城市不断扩大，许多用户工作地点与家距离较远，导致用户的工作区域与生活区域不相同，仅仅依靠两个兴趣点之间的距离而不考虑区域这种粗粒度信息来进行推荐，会导致推荐的兴趣点只停留在工作区域或生活区域，这可能与用户在不同时间段跨区域活动的需求不相符。因此，在对下一兴趣点推荐时，应该将每个时间段内用户所在的区域信息作为一个考虑因素。

众所周知，LBSN 是一个可以提供位置信息的社交网络，它可以让用户随时随地获取经纬度信息并与好友进行分享。因此，用户下一签到的兴趣点可能会受到用户在LBSN 中的朋友（或称为社交影响）的影响，朋友访问兴趣点信息可以在一定程度上弥补用户访问兴趣点的数据稀疏这一问题。已有研究通过结合朋友评价信息来提升推荐准确性，例如文献[5]通过朋友的评论信息对用户进行推荐，但仅有少量用户对兴趣点产生评价。因此，这些研究仍存在数据稀疏性的问题。

可见，下一兴趣点推荐还存在一定局限性。为此，本文采用残差网络模型研究不同签入特征对用户签到兴趣点的影响。一是将某一时刻兴趣点的区域信息作为影响因素之一融入到用户签到兴趣点序列中，进一步改善数据稀疏问题，提高推荐准确性。同时采用残差网络模型处理区域与用户访问的兴趣点序列，使用残差网络中跳跃连接来不断优化模型，可有效降低训练模型的参数误差，进而提升兴趣点推荐的准确性。二是考虑社交网络中朋友签到兴趣点对用户的影响。已有研究大多是构建位置信息和社交信息的异构网络，通过提取朋友评论信息来辅助用户推荐，但仍存在一定局限性。本文融合朋友签到的兴趣点与用户签到的兴趣点，可以有效扩大用户兴趣点的推荐范围，更好地解决数据稀疏问题。本文的主要贡献如下：

（1）提出一种融合区域与朋友影响的下一兴趣点推荐模型。引入不同时间段内签到兴趣点所属的区域，将某一时刻的兴趣点和某一时刻的区域相结合，不仅可以改善数据稀疏问题，也可提升下一兴趣点推荐的准确性。同时将可信任的朋友签到的兴趣点与用户签到的兴趣点进行融合，进一步提高用户下一兴趣点推荐的准确性。

（2）提出一种残差连接的结构对兴趣点序列进行训练。通过跳跃连接构建残差块，改善梯度消失和网络退化的问题，提升模型的准确性。

（3）通过对比实验，证明本文提出的模型的准确性明显优于其他推荐模型。

1 相关工作

1.1 基于传统算法的下一兴趣点推荐

传统的下一兴趣点推荐算法主要包括协同过滤推荐、基于马尔可夫链的兴趣点推荐。

协同过滤（collaborative filtering）是比较成熟的兴趣点推荐算法。已有的基于模型的协同过滤算法[1]，是从用户签到兴趣点信息中分析用户对兴趣点的偏好。然而，协同过滤算法将用户访问的兴趣点都考虑在一个整体中，忽略了访问兴趣点之间的作用。

基于马尔可夫链的兴趣点推荐算法是传统下一兴趣点推荐算法中最常见的方法之一。基于马尔可夫链的推荐算法主要分为基于加性马尔可夫链的算法和基于隐马尔可夫链嵌入的算法。Zhang 等人[2]提出采用加性马尔可夫链算法，考虑了序列对兴趣点推荐的影响，通过挖掘序列模式将兴趣点序列转化成动态位置转换图，从而预测用户访问兴趣点的概率。而Feng 等人[6]提出使用马尔可夫链将兴趣点嵌入到欧几里德空间中，根据兴趣点之间的欧几里德距离计算兴趣点之间的转移概率。基于马尔可夫链的下一兴趣点推荐系统的缺点是显而易见的，因为马尔可夫链的属性是假定当前的交互仅依赖于一个或几个最近的交互，所以它们只能捕获相邻的兴趣点之间的关系，而忽略了之前访问的兴趣点对其产生的影响。这说明它只能捕获兴趣点与兴趣点之间的依赖，而忽略了用户与兴趣点交互的集体依赖。

1.2 基于深度学习的下一兴趣点推荐

大多数对下一兴趣点推荐的研究主要采用深度学习的模型建立用户与兴趣点之间的关系。最常用的是递归神经网络（recursive neural network，RNN），它不规定访问兴趣点的数量。例如，Mikolov 等人[7]提出使用递归连接，考虑访问兴趣点之间的影响；Liu等人[8]采用RNN，通过用户历史访问兴趣点序列来预测下一个可能访问的兴趣点。然而，仅仅使用RNN捕获历史访问兴趣点之间的关系是困难的，因此除了基本RNN 外，目前比较流行的是使用RNN 的变形,即LSTM（long short-term memory）、GRU。例如，Xu等人[9]通过忘记门、输入门、输出门来捕获长短期记忆。基于RNN 的方法还处于早期阶段，没有强调历史访问信息对用户当前访问兴趣点的影响，为此Wang 等人[10]使用基于门控电流单位的RNN（GRU），捕获序列中的长期依赖性。

1.3 基于社交和区域化的下一兴趣点推荐

最近，下一兴趣点推荐问题也考虑了其他影响因素，如基于社交关系的朋友推荐和基于区域化的推荐。其中兴趣点推荐可以让用户签到一个兴趣点时能够满足其特定的需求。然而在LBSN 中，用户访问的兴趣点数据是比较稀疏的，无法准确地获取从未签到过的兴趣点。为了使数据更加准确，Ye等人[11]提出通过社交关系来提高兴趣点推荐方法的准确性。目前已有的兴趣点推荐模型大多采用不同的显性社会关系。例如，Xu 等人[12]提出的模型是采用LBSN 进行推荐；Zhao 等人[5]提出使用异构网络对兴趣点进行推荐，将基于社区的社交网络与基于地理位置的社交网络相结合。考虑到朋友之间的隐性关系也对用户有很大的影响，Pan 等人[13]提出隐性朋友和显性朋友对用户访问兴趣点的影响。

最近的许多研究表明，用户签到兴趣点和兴趣点之间的距离存在密切的联系，因此大多数下一兴趣点推荐模型主要通过利用地理影响来提高推荐的准确性。例如，Xiong 等人[14]将区域聚集成环形，但这种方法很难发现区域的中心兴趣点。考虑到用户访问的兴趣点可能受到邻近区域影响，Feng 等人[15]使用建立二叉树的方法将一个兴趣点分配给多个区域，通过个人兴趣和人群偏好等因素，结合区域信息对用户签到兴趣点进行推荐。

不同于已有模型，本文提出结合朋友访问的兴趣点以及兴趣点所属区域对用户的影响，将区域信息嵌入到用户签到兴趣点序列中，采用残差网络进行训练。同时将朋友访问的兴趣点与其进行融合，以提高对下一兴趣点推荐的准确性。

2 问题描述与相关定义

本章首先将兴趣点推荐问题形式化，然后介绍重要的定义和符号。

问题描述：给定一个包含朋友关系的基于地理位置的社交网络的数据集（Foursquare、Gowalla），其中包含兴趣点（point of interest，POI）的位置和所有相关用户的社交信息。POI预测的目标是给目标用户u推荐可能访问的POI列表。

为了便于理解，表1 描述了本文使用的重要符号。同时为了便于描述本文提出的方法，这里先给出一些相关定义。

定义1（朋友）在社交网络中，每个用户可有多个朋友，而每个用户还可能有多种角色，用户与朋友之间的联系代表他们之间的交流。本文中朋友由F表示。

Table 1 Notations used in this paper表1 本文中的符号

定义2（区域）区域是指根据用户访问的地理位置，按照一定的范围进行聚类。本文认为一个区域内的兴趣点有很高的密度，但是区域与区域之间的关系比较稀疏。本文中区域由R表示。

定义3（兴趣点）兴趣点是用户访问一个地点的唯一标识（例如公园、健身房等）。在本文提出的模型中兴趣点由两个特征表示，即兴趣点编号和兴趣点的地理位置（由经度、纬度表示）。本文中兴趣点由P表示。

概念1（残差网络）如图1 所示，残差网络是堆积层结构，identityx代表恒等映射输入向量x。当输入为x时，其学习到的特征记为H(x)，可以学习到残差F(x)=H(x)-x。其实原始的学习特征是F(x)+x，当残差为0 时，此时堆积层做了恒等映射，至少网络性能不会下降。而实际上残差不会为0，因此残差网络直接将输入信息绕道传到输出，以保证信息的完整性。采用残差网络在反向传播过程中，梯度连乘，不会造成梯度消失[16]。

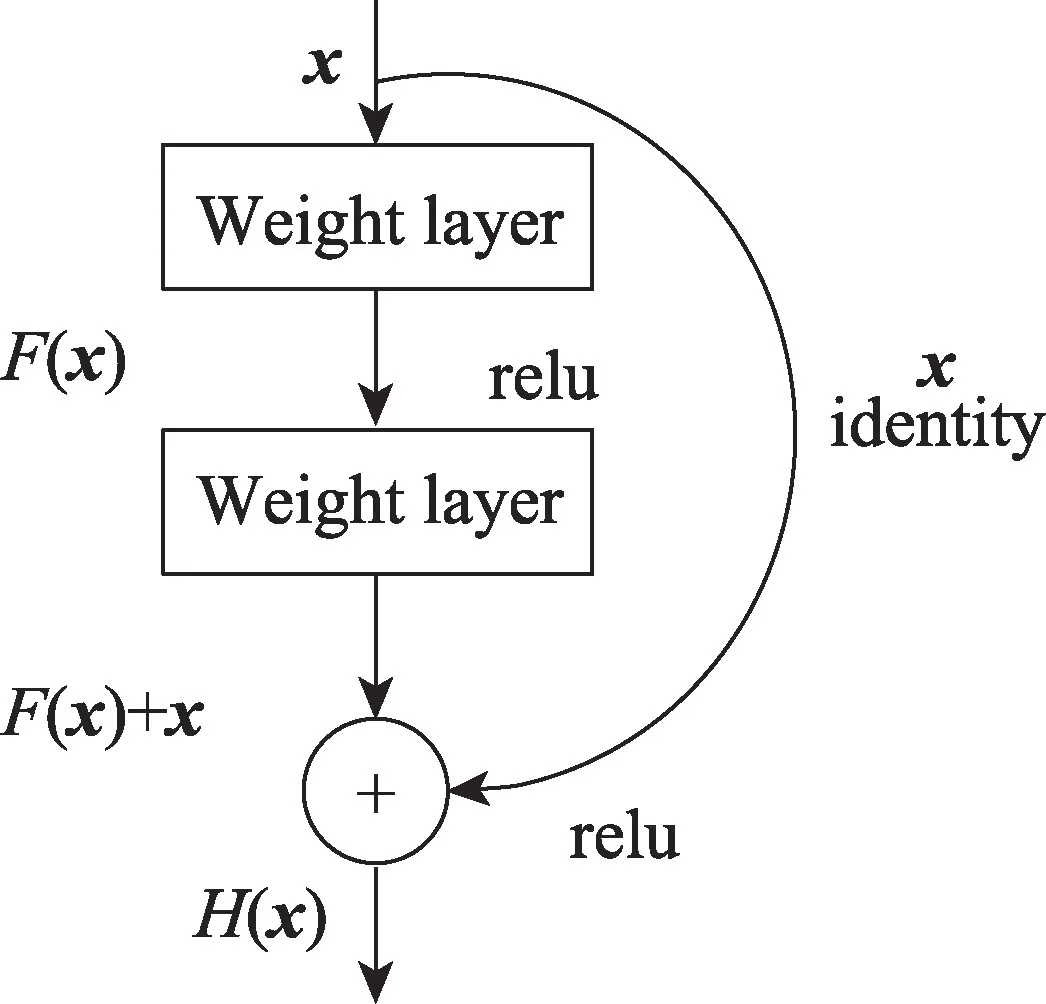
Fig.1 Residual block of residual network图1 残差网络的残差块

在深度神经网络训练中，随着网络层次的增加，理论上可以取得更好的结果。但是实验却发现残差网络中的一个新的思想[17]，通过冗余层完成恒等映射，保证输入向量经过恒等层时保持不变。残差网络在网络训练时自己可以判断哪些是恒等层。

3 融合区域与朋友影响的下一兴趣点推荐

下一兴趣点推荐与一般的推荐任务（如商品、电影、新闻推荐）不同，因为下一兴趣点推荐具有高度的时空依赖性，所以人们在现实生活中更倾向于访问时空距离较近的，如近期访问过的且距离较近的电影院、餐馆等。这说明用户更倾向于访问自己熟悉的且距离自己较近的兴趣点。然而用户对兴趣点的选择是一个复杂的过程，往往受到众多因素的影响，其中社交因素和地理因素是最重要的两个因素。地理因素显著影响用户的移动行为，可以有效地提高推荐质量，而社交关系可以通过朋友签到的兴趣点弥补数据稀疏性。

本文主要通过将不同的影响因素与用户签到序列相结合，以提高推荐的准确性。本文认为用户签到下一兴趣点不仅与其自身相关，朋友相互之间的影响、区域的变化也是其选择的考虑因素。因此，从社交网络中朋友关系以及在不同时间段内用户所在的区域入手，提出融合朋友与区域信息的下一兴趣点推荐模型。如图2 所示，融合朋友与区域信息的下一兴趣点推荐模型主要由残差网络训练区域与用户签到兴趣点序列、朋友访问中心兴趣点、融合朋友与区域影响的下一兴趣点推荐三部分组成。基于前人的研究结果，根据用户签到兴趣点的特征以及用户签到序列来选择合适的主题模型，对用户下一签到的兴趣点进行推荐。

3.1 残差网络训练区域与用户签到兴趣点序列

残差网络训练区域与用户签到兴趣点序列，主要由用户访问兴趣点所属区域以及将区域与兴趣点嵌入到残差网络中两部分组成。接下来，将分别介绍这两部分。

3.1.1 用户访问兴趣点的区域

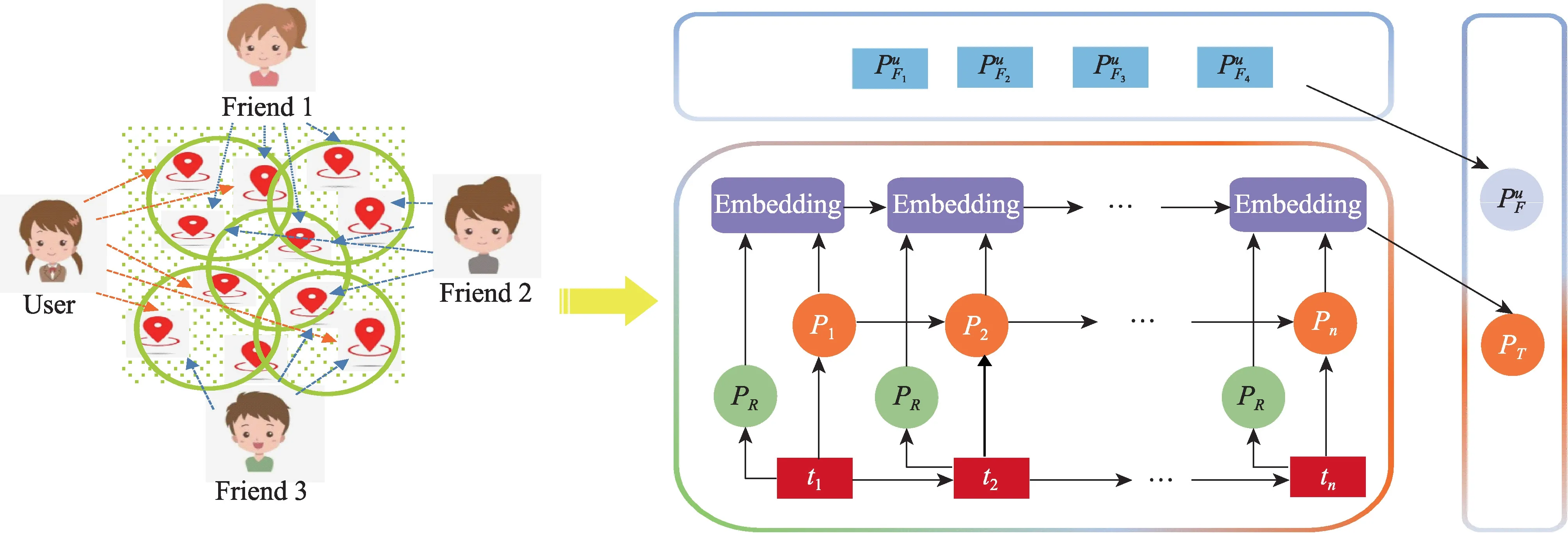
Fig.2 Next POI recommendation model which integrates influence of regions and friends图2 结合朋友与区域信息的下一兴趣点推荐模型

用户访问的兴趣点不仅与兴趣点之间的距离有关，与区域也是有关的，因此区域也应该作为兴趣点推荐时考虑的因素之一。目前大多数的工作虽然考虑到了用户在连续访问不同兴趣点时距离的影响，但也仅仅停留在相邻两个兴趣点的距离计算上。因为用户在不同时间段访问的区域不同，所以确定用户属于哪一区域并根据区域进行推荐可以提高准确性。该方法假设大多数人的日常生活是有规律的，并且他们的偏好在一定时期内很少改变，因此日常活动的范围将局限于几个相对较小的区域。如图3所示为用户访问兴趣点的区域（R1、R2、R3）划分，用户在短时间内访问的兴趣点主要集中在同一区域。

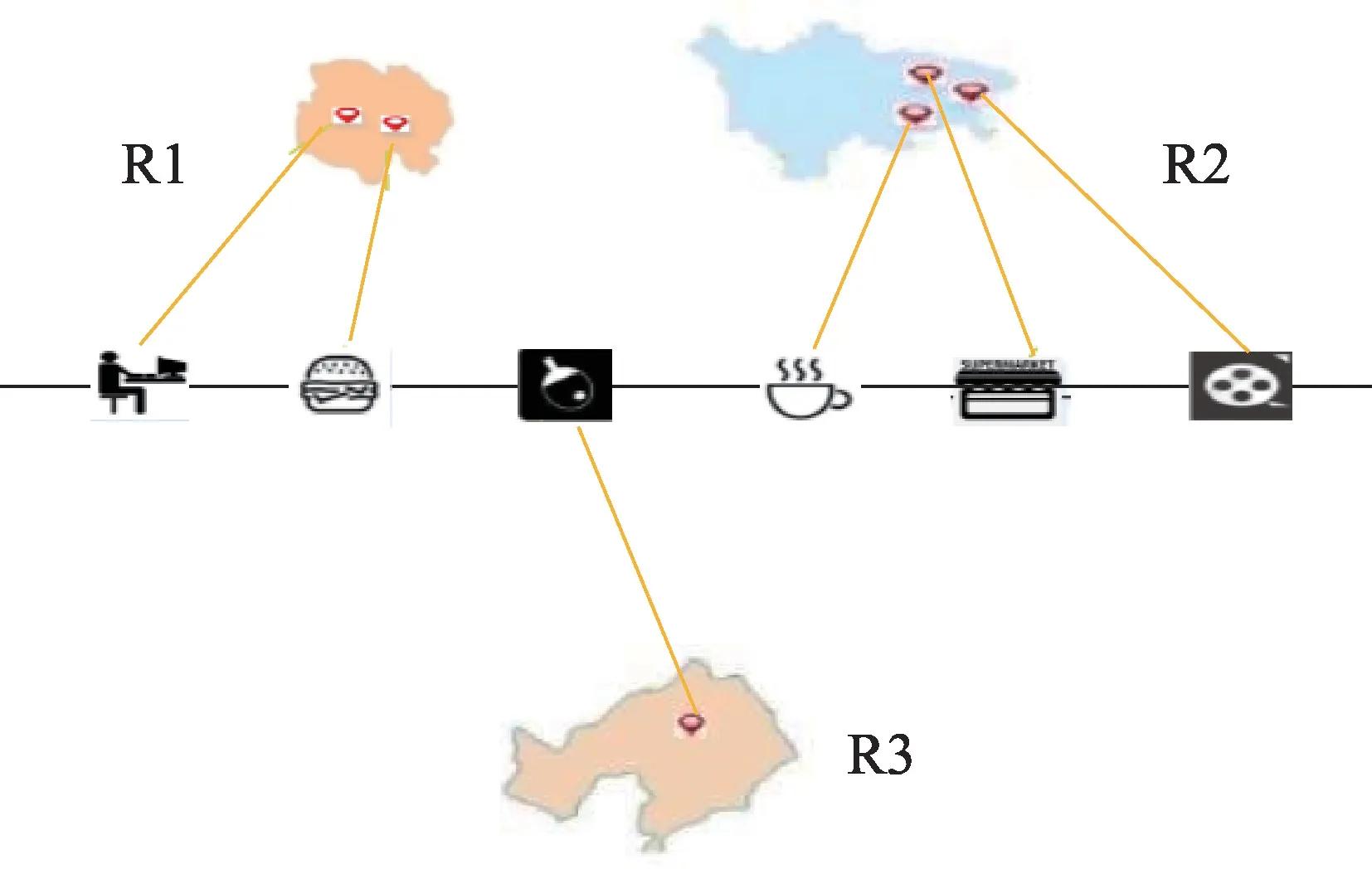
Fig.3 Region division of user check-ins图3 用户访问兴趣点的区域划分

区域是影响用户访问的兴趣点序列和用户偏好的一个重要因素，而现有的基于频率的softmax 结构不能捕捉到兴趣点所属的区域。因此本文采用聚类算法，将用户历史访问的兴趣点进行聚类，划分出区域。区域划分算法见算法1。

算法1区域划分

输入：用户访问的兴趣点。

输出：区域R，n代表区域的个数。

1.创建K个作为起始区域的中心兴趣点xj（随机选择）

2.当任意的区域R分配结果发生改变时

3. 访问数据集中的

4. 对每个区域R的中心兴趣点xj

5.dist=xj-

6. 将兴趣点分配到距其最近的区域R

7. 对每一个区域R

8. 求出均值并将其更新为区域的中心兴趣点xj

通过欧几里德距离算法，计算用户历史访问的兴趣点属于哪一区域，根据每个区域的中心点，计算用户在该时刻签到的兴趣点与每个区域的中心兴趣点的距离。选取距离最小的为该兴趣点所属的区域。兴趣点与区域中心点的距离计算公式如下：

其中，代表用户u在某一时刻访问的兴趣点，xj代表区域的中心兴趣点。

3.1.2 区域与兴趣点嵌入残差网络

本部分研究的目的是综合考虑用户下一签到兴趣点受到上一兴趣点以及区域的影响因素。首先寻找目标用户的连续签到序列，然后根据目标用户的连续签到序列和用户访问兴趣点的区域，共同构建区域与用户访问兴趣点嵌入的模式序列，并采用残差网络进行训练。例如，采用残差网络训练模型时将一个用户访问的n个兴趣点以及嵌入的区域构建一组序列，具体使用残差连接对序列进行训练，过程如图4 所示，其中圆点代表区域与用户访问兴趣点的嵌入序列，虚线块代表构建的残差块。

Fig.4 Residual connection based check-in sequence图4 基于残差连接的签到序列

残差网络方法是在用户访问的兴趣点序列上增加跳跃连接，每两层增加一个捷径，构成一个残差块，如图4 所示，由3 个残差块连接在一起构成一个残差网络。在处理用户访问兴趣点的时候，不仅与自身兴趣点有关，还与上一兴趣点甚至更早的兴趣点有关，因此需要用残差网络处理梯度消失问题。主要采取的算法是该用户在这一时刻签到的兴趣点以及区域H(x)=x，即输入是x，经过该冗余层后，输出仍然为x（如图4 中的第一个虚线块所示）。但要想学习H(x)=x恒等映射时的这层参数是比较困难的。残差网络能够采用跳跃连接避免去学习该层恒等映射的参数，让H(x)=F(x)+x，这里F(x)称作残差项，学习F(x)比学习H(x)简单，因为一般每层网络中的参数初始化偏向于0，这样更新该网络层的参数来学习H(x)=x，该冗余层学习F(x)=0 的更新参数能够更快收敛。一个残差单元的公式如下：

其中，y和x均为残差块所在层的输入与输出向量，函数F(x,wi)为训练残差映射所学习到的每个残差块。

采用残差网络训练区域与用户签到兴趣点构建的序列公式如下：

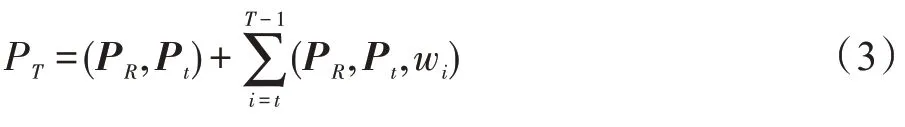
其中，PT代表用户推荐的下一时刻的访问兴趣点，PR代表区域向量，Pt代表用户某一时刻访问的兴趣点向量。

3.2 朋友访问中心兴趣点

本文考虑到朋友对用户访问兴趣点是有影响的，因此将用户的多个朋友访问多个兴趣点进行向量融合，即计算多个朋友在多个时间访问兴趣点的中心点。由于朋友访问兴趣点可能存在偶然性，如出差这种情况，会导致数据比较分散，求出的朋友访问的中心点不准确。因此本文设定一个阈值，只考虑一定范围内朋友访问的兴趣点。多个朋友访问兴趣点融合公式如下：

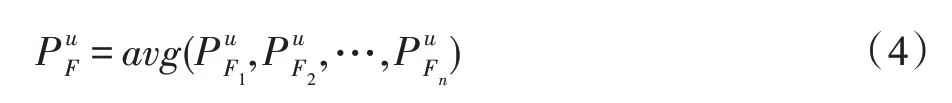
其中，代表用户u所有朋友访问兴趣点的中心兴趣点，代表用户u的一个朋友访问的兴趣点，通过数据预处理得到其朋友访问的兴趣点。

3.3 融合朋友与区域影响的下一兴趣点推荐

为了捕捉用户u访问兴趣点的区域和朋友影响，将残差网络处理区域与用户访问兴趣点序列的输出和朋友访问中心兴趣点向量连接在一起。如图5 所示，采用残差网络将区域向量嵌入到用户历史签到兴趣点序列中，与朋友访问兴趣点向量进行拼接。

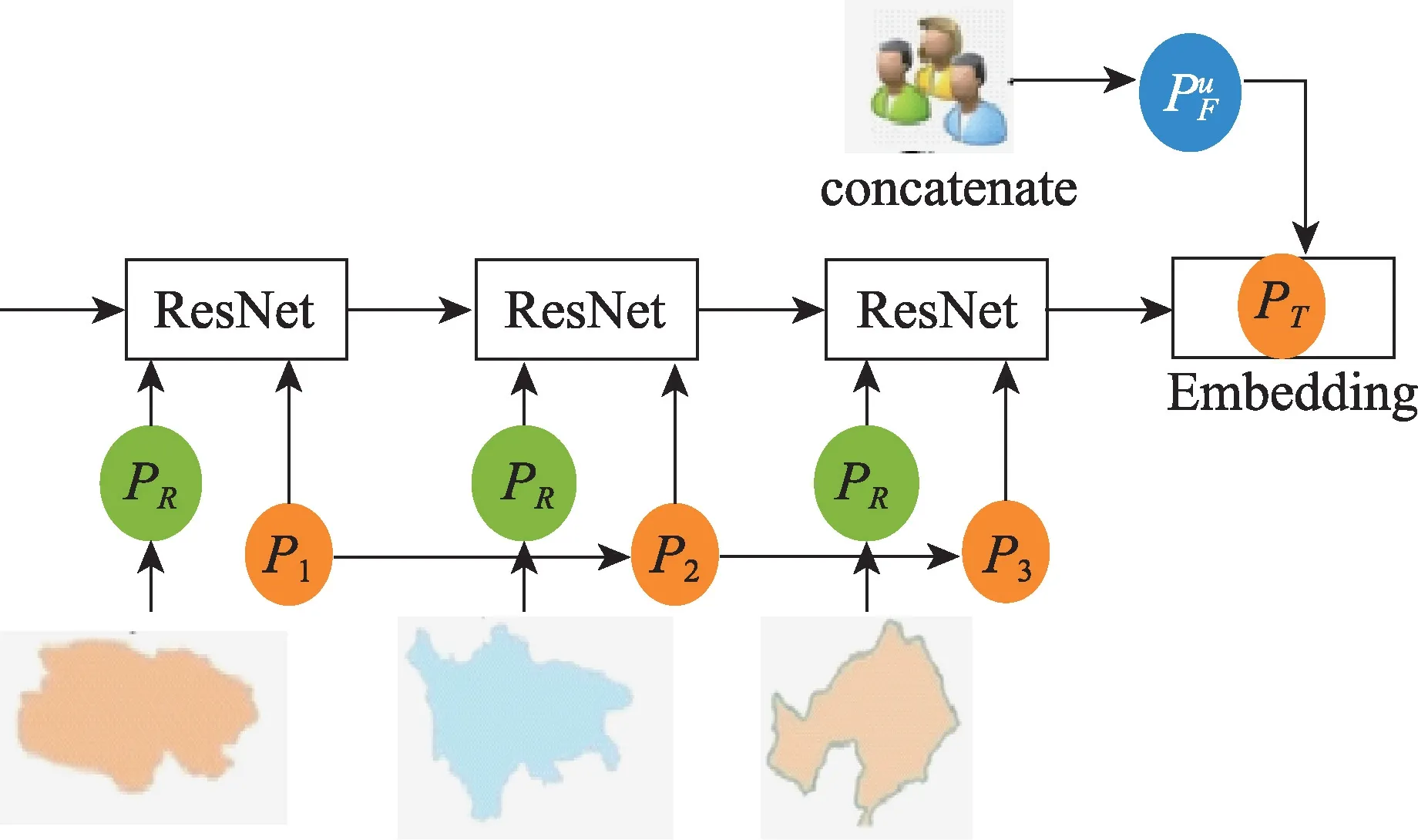
Fig.5 Next POI recommendation:fusing region factor and friends'information图5 融合区域、朋友信息的下一兴趣点推荐

融合朋友与区域影响的兴趣点推荐公式如下：

其中，w′和b′分别是输出层的权重矩阵和偏差项。PT代表融合区域后用户推荐的下一时刻的访问兴趣点，代表用户u所有朋友访问兴趣点的中心兴趣点，代表融合朋友与区域影响的下一兴趣点推荐。

4 实验与分析

本章展示了所提出的融合区域与朋友影响的下一兴趣点推荐模型的实验结果，通过与最新工作比较来评估本文提出的模型（Proposed）的有效性。

4.1 实验数据集

本文在两个数据集上进行实验以验证模型的可行性，其中所使用的数据集为兴趣点推荐研究常用的数据集，分别为Foursquare、Gowalla 数据集，在这两个数据集上进行预处理，具体见表2。

Table 2 Statistics of datasets表2 数据集统计

Foursquare 数据集：Foursquare 社交网络可以提供许多基于位置的信息，例如兴趣点登记。该数据集来自美国加利福尼亚州旧金山地区的4 163 名用户，包括身份、姓名、登记时间和经纬度信息。

Gowalla 数据集：Gowalla 是一个典型的LBSN，用户可以随时共享其位置信息。签到数据由签到时间、地点、用户ID 和用户的社会关系构成。数据收集了用户在2009 年2 月至2010 年10 月期间6 442 890次签到信息。

4.2 对比实验

为了验证本文提出的推荐模型的可行性，设置了一些对比实验，所要对比的流行算法如下：

LORE[2]：提出采用挖掘序列模式的模型。将用户访问的兴趣点表示为动态位置转换图，并采用马尔可夫链预测用户访问兴趣点的概率，同时将地理影响和社会影响融合到一个统一的推荐框架中。

PRME[6]：提出一种个性化的等级度量嵌入方法。采用度量嵌入的方法进行推荐，结合了兴趣点序列、用户偏好和地理影响。

RNN[8]：提出距离偏好对下一个POI 的影响。将用户的顺序偏好和连续兴趣点之间的距离通过RNN模型进行训练，通过融合空间偏好和顺序偏好对下一兴趣点进行推荐。

POI2Vec[15]：提出结合地理因素影响的潜在表示模型。考虑用户的个人偏好和签到兴趣点序列顺序的影响，给潜在的用户推荐兴趣点。

FPMC[18]：提出一个矩阵分解和马尔可夫链相结合的模型。每一个用户对应一个转移矩阵，同时引入个性化排序的框架来处理签到数据。

Proposed：本文提出的融合区域与朋友关系的用户下一兴趣点推荐模型，采用残差网络模型将用户签到兴趣点的信息与兴趣点所属区域信息进行嵌入训练，避免网络退化。通过融合朋友信息，缓解数据稀疏性，提高推荐的准确性。

4.3 评价标准

本文研究的关键问题是如何准确地给目标用户推荐下一时刻访问的兴趣点。本文使用准确率（Precision）、召回率（Recall）来检查和验证融合区域与朋友影响的用户访问兴趣点模型的有效性，其定义如下所示，分别为：

4.4 结果与分析

4.4.1 本文模型的测试结果

本实验在两个数据集上测试本文模型的准确率、召回率得分，表3 展示了本文模型在Top5、Top10、Top15、Top20、Top25 时的准确率、召回率的实验结果。实验中，通过80%、10%、10%划分数据集，并进行反复实验。采用的残差网络一共24 层，每一层卷积核数量为24，卷积核大小为8。

4.4.2 与基线模型对比与分析

本实验选取当基线模型具有自己最佳表现时采用的参数值，分别在Foursquare 和Gowalla 数据集上，测试了本文模型和基线模型的推荐准确率和召回率，对比结果见图6、图7 和图8、图9。

测试结果如下：

（1）从图6 和图8 中可以看到，FPMC 的各项推荐表现都是最差的，并且图7、图9 也显示FPMC 的召回率得分也是最差的。这是因为FPMC 方法只关注于从用户的签到历史数据中挖掘用户的偏好信息，而没有考虑任何用户签到兴趣点的影响因素。

（2）PRME 和POI2Vec 这两种模型的实验结果都略好于FPMC 方法。这是因为这两种方法分别结合了地理信息和个人偏好信息。其中PRME 将个人偏好和地理影响嵌入到基于成对排序度量框架中。而POI2Vec 结合兴趣点地理坐标构建二叉树的方法，将兴趣点分到不同的区域中，在每个区域的兴趣点上构建一个二叉树。通过这两种方法验证了影响因素对兴趣点推荐是有效的。

Table 3 Accuracy and recall of proposed model表3 本文模型的准确率、召回率

Fig.7 Comparison of recall on Foursquare图7 在Foursquare数据集上的召回率对比

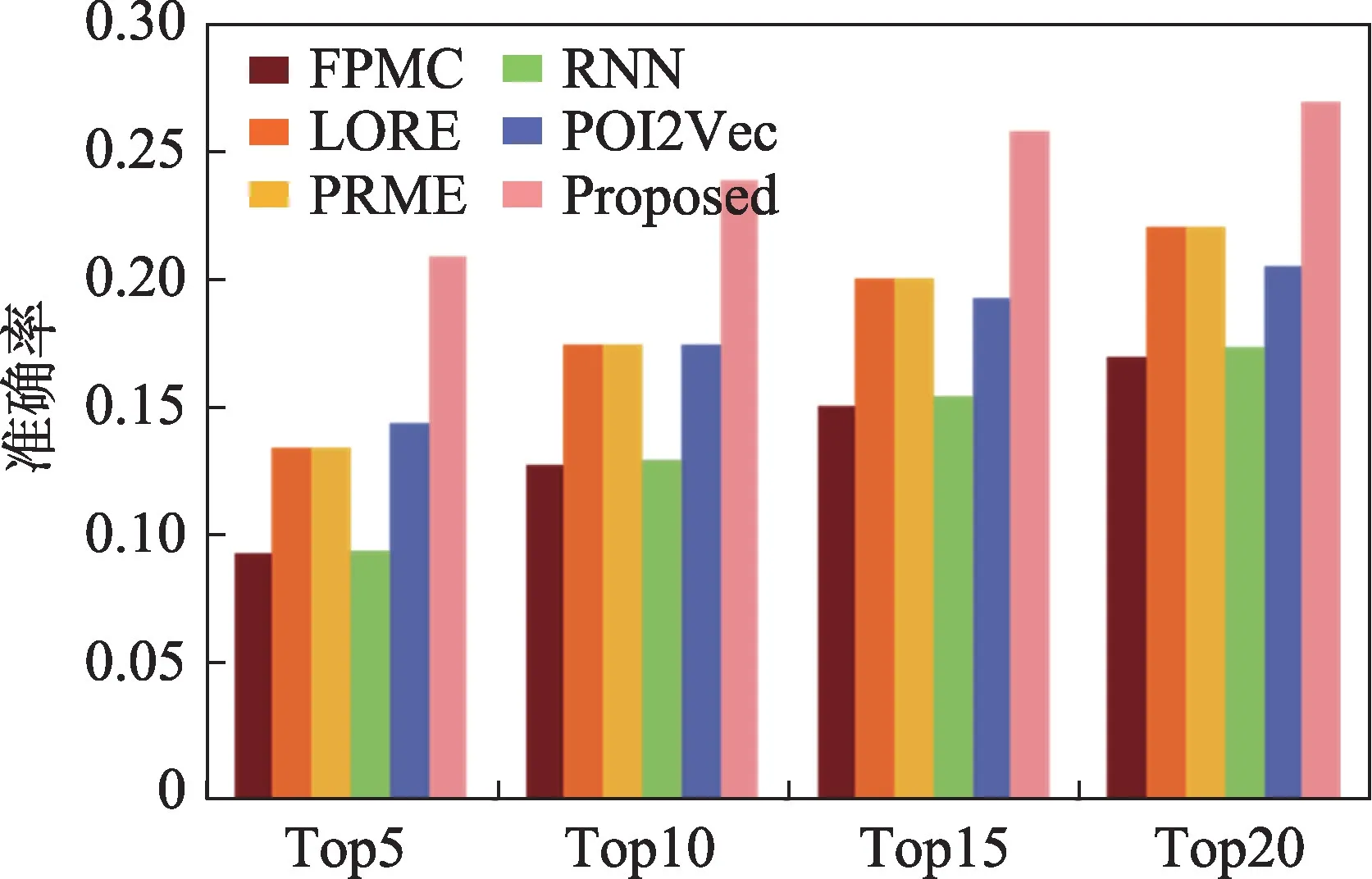
Fig.8 Comparison of accuracy on Gowalla图8 在Gowalla 数据集上的准确率对比

（3）LORE 表现出了较好的推荐性能。LORE 采用马尔可夫链给用户推荐一个最可能访问的兴趣点，并将访问兴趣点之间的顺序、地理影响和社交关系融合到一个统一的推荐框架中。LORE 的实验数据表明社交关系对下一个兴趣点推荐起到重要作用，同时也说明了马尔可夫链对下一个兴趣点推荐的有效性。但LORE 在推荐下一个兴趣点时没有将待推荐的兴趣点限制在一个局部区域内，这也是限制其推荐性能的一个因素。

（4）RNN 通过对给定的兴趣点顺序依赖性和空间偏好建模来推荐下一个可能访问的兴趣点。从表3中可以观察到RNN 对下一兴趣点推荐的准确率较低，这说明随着连续访问兴趣点的数量增多，采用深度学习框架存在梯度消失和退化的问题。

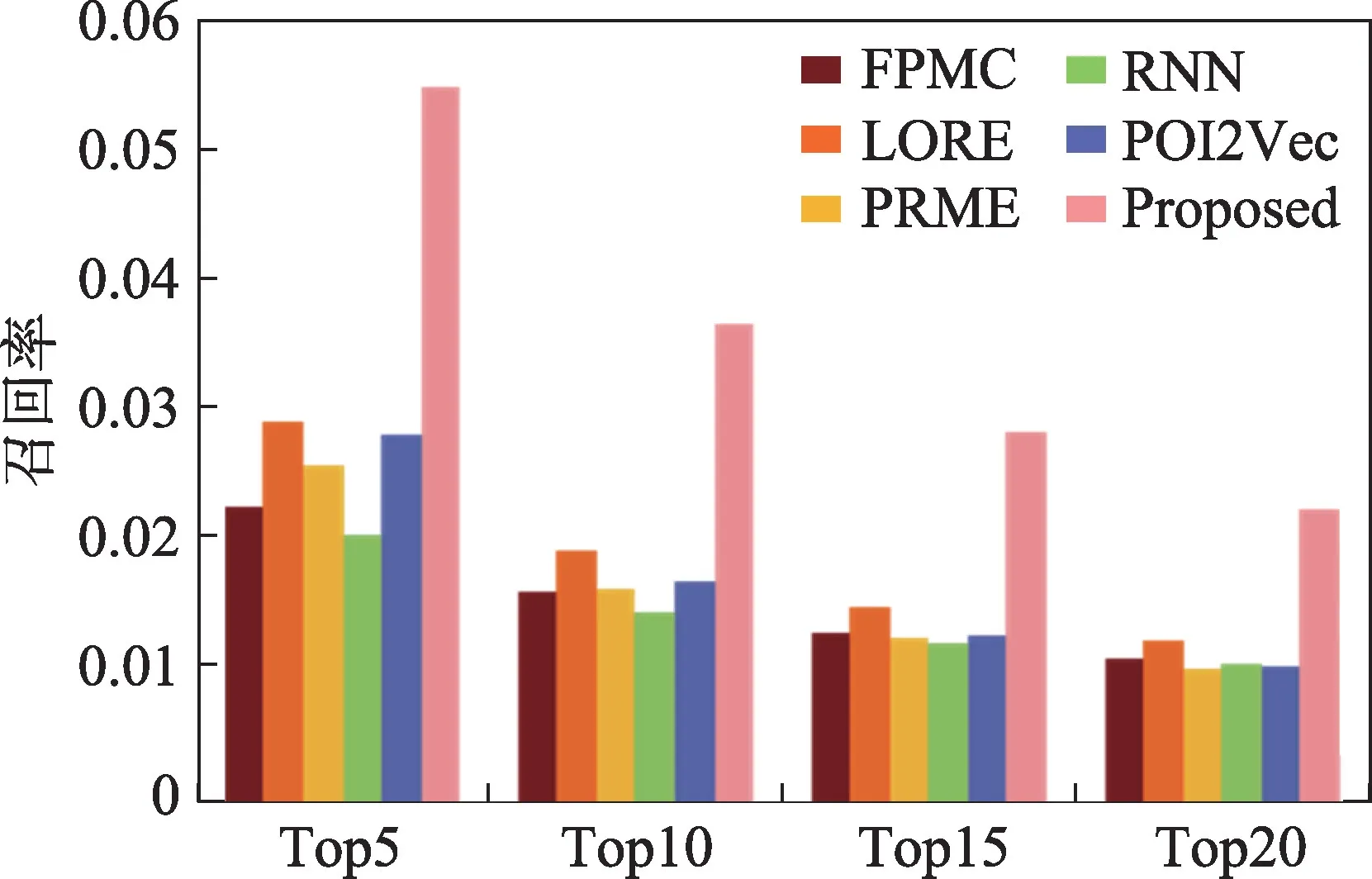
Fig.9 Comparison of recall on Gowalla图9 在Gowalla 数据集上的召回率对比

总体上，本文模型在准确率、召回率得分方面的性能始终优于基线模型，主要是将区域与朋友影响有效地集成到统一的推荐过程当中，并考虑访问兴趣点的先后顺序。通过综合兴趣点所属区域，将区域信息与用户签到兴趣点序列进行嵌入，捕获粗粒度信息动态地预测用户的偏好。同时将朋友签到兴趣点与嵌入区域的用户签到兴趣点进行融合，克服了签到数据稀疏的问题。同时本文采用了残差网络，通过增加跳跃连接层构成残差块[17]，将输入信息绕道传到输出，保证信息的完整性。同时在反向传播过程中，梯度连乘，不会造成梯度消失[16]，因此它不会像RNN 随着网路层次的加深，而发生准确率下降的问题。

4.4.3 不同用户序列窗口长度的影响

用户序列窗口长度是融合区域和朋友影响的用户访问兴趣点模型的重要因素，本文在两个数据集上设置不同长度的用户序列窗口进行实验。表4 说明了在用户序列不同长度窗口下评估本文推荐模型的准确性。在Foursquare 数据集上，可以观察到，当用户序列长度为25，取Top20 时，模型获得了最佳的预测性能。在Gowalla 数据集上，当用户序列长度为10，取Top20 时，模型获得了最佳的预测性能。同时观察到，即使用户序列的长度不是最佳的，本文模型的性能也优于最先进的模型。

Table 4 Influence of window length of check-in sequence on model accuracy表4 访问序列的窗口长度对模型准确性的影响

4.4.4 本文方法中不同因素的影响

本文在用户签到兴趣点序列中嵌入了区域信息和朋友签到兴趣点信息，为了评估这两种嵌入信息的性能，本小节将本文模型和只考虑区域信息或只考虑朋友信息的模型在用户序列窗口长度为10，取Top5时的性能进行了比较。如图10 所示，在Foursquare数据集上，本文模型分别与只考虑区域信息的模型和只考虑朋友信息的模型进行比较，本文模型在准确度上分别提高了0.131 和0.074。在Gowalla数据集上，本文模型在准确度上分别提高了0.083 和0.042。可见，融合区域或朋友信息都提高了推荐的准确性。

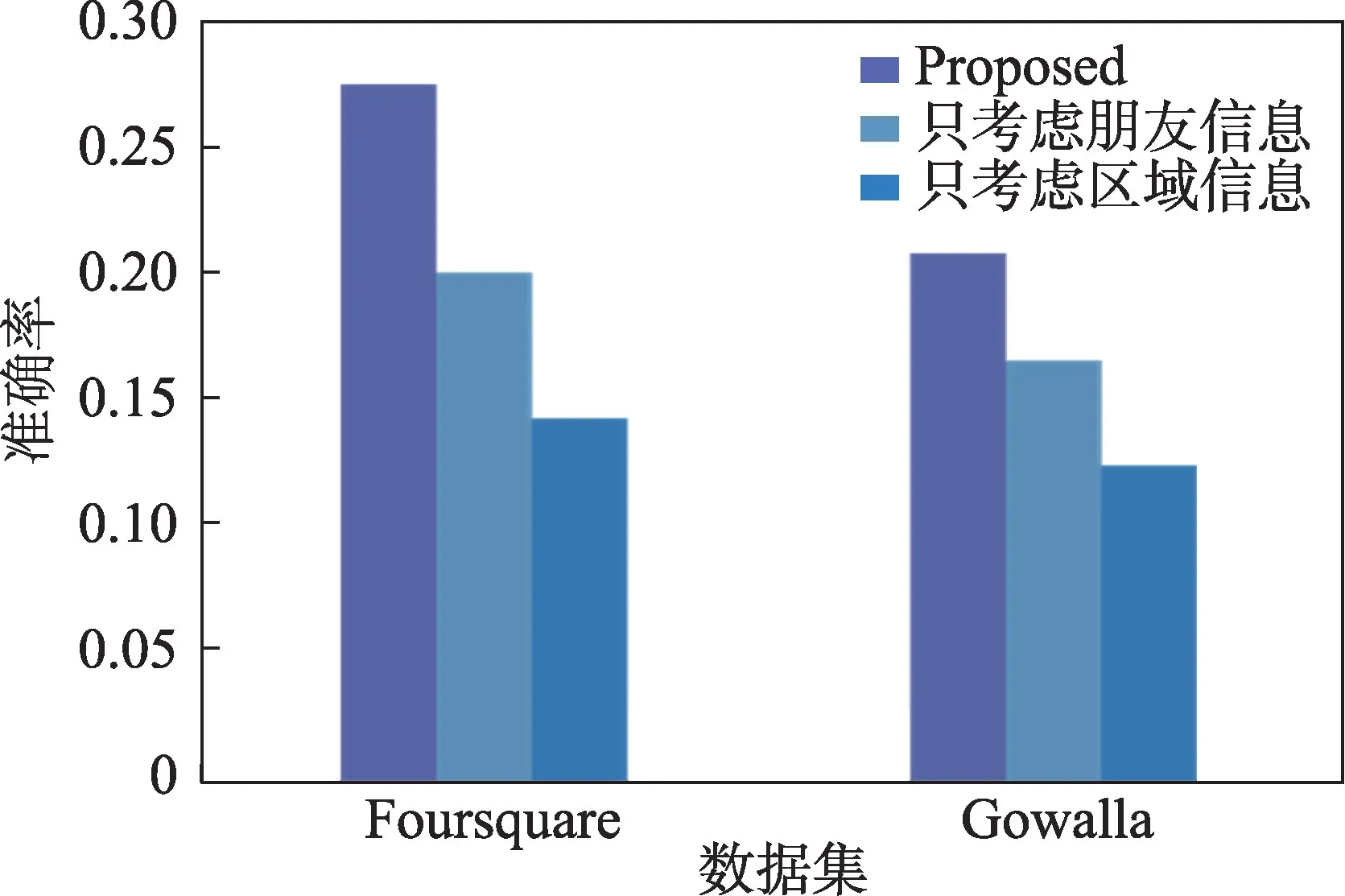
Fig.10 Influence of different factors on performance of proposed model图10 不同的因素对本文模型性能的影响

5 结束语

本文提出了融合区域与朋友影响的用户访问兴趣点的推荐模型。该模型充分利用了残差网络避免网络退化的问题来进行序列推荐。利用区域影响因素捕获粗粒度信息，同时利用朋友访问兴趣点的信息避免数据的稀疏性。在两个真实数据集上的实验结果表明，本文提出的模型在推荐准确性上明显优于其他对比模型。接下来，会进一步围绕上述两种影响因素对用户签到兴趣点的影响进行研究，争取获得更深层次的发现。