基于模型预测控制的无人机时空协同航迹规划

顾海艳，陈 亮，王多点

1.江苏警官学院 计算机信息与网络安全系，南京 210031

2.陆军工程大学 野战工程学院，南京 210007

3.军事交通学院 汽车士官学校，安徽 蚌埠 233011

4.陆军研究院，北京 100089

近几十年，有关多无人机技术的研究迅猛发展。其中，多无人机协同航迹规划是无人机执行任务的关键技术之一。多无人机协同航迹规划研究无人机航迹之间的协同关系，包括空间协同和时间协同[1]。空间协同即避碰问题，要求无人机能够发现并消除碰撞冲突。时间协同，要求所有的无人机在执行任务时满足一定的时序约束或时间窗约束。

空间协同的方法主要有两类：一类是几何算法[2-3]，通过分析成对无人机几何空间的相对运动关系，提供被动式避碰策略。几何法是解决碰撞问题最直观的方法，然而几何法只能有效消解成对无人机间的冲突，不适用于多无人机协同避碰。另一类是将避碰问题转化为最小安全间隔约束条件下的航迹规划问题进行求解。求解的算法主要有人工势场法[4-5]、线性规划法[6-7]和模型预测控制（Model Predictive Control，MPC）[8-9]等方法。其中，人工势场法是集中式算法，只适用于固定障碍物的情况，并不适合分布式或动态障碍物的情况[10]；线性规划法也是集中式算法，并且随着飞机数量的增加，计算量呈几何指数上升；基于滚动优化思想的MPC能够显式地考虑各种变量的约束，并滚动实施控制输入，天然具有实时分布式控制的特点，因此该方法在无人机避碰问题中得到广泛应用[11-12]。文献[13]采用模型预测控制方法将编队重构避碰问题转化为滚动优化问题，并采用微分进化方法求解。文献[14]提出了一种改进的基于分布式的非线性MPC方法，设计的冲突消解算法不仅能够计算每个无人机的控制量，并能确保无后续冲突。文献[15]基于模型预测控制方法提出了一种实时机间避碰的多无人机协同航迹规划方案。然而，以上研究仅考虑了无人机空间协同。

时序协同是时间协同的重点研究内容，而同时到达则是时序协同中最具研究价值的方向之一。文献[16-17]研究了基于协调变量和协调函数的多无人机协同航迹规划算法，但该方法本质上是集中控制方法，存在信息交互大、计算复杂和鲁棒性差的缺点。文献[18]基于一致性理论的分布式控制结构，设计了结合航迹规划与轨迹控制的策略以实现多无人机同时到达的目的。文献[19]针对复杂网络，提出了基于合作博弈的最优一致算法解决多无人机在任务区域的集结问题。文献[20]提出一种基于精英保持策略的分布式协同粒子群优化算法解决多无人机编队集结问题。然而，以上文献仅考虑了时间协同。

综合以上分析可见，虽然模型预测控制在无人机避碰问题中应用广泛，但同时实现空间协同和时间协同的方法却鲜见于文献。本文针对多无人机时空协同问题，提出了基于模型预测控制的无人机在线协同航迹规划的方法。为了达到同时满足多无人机空间协同和时间协同的目的，改进了碰撞冲突消解规则，设计了时间冲突消解规则，并采用优先级的方法实现空间协同和时间协同的解耦。仿真实验验证了本文方法能够有效实现多无人机时空协同。

1 问题描述

假设某次任务中，要求NV(NV＞1)架无人机对任务区内NT(NT≥1)个目标发起攻击。为使攻击的发起具有突然性，要求无人机同时到达目标。同时，需要确保无人机在飞行过程中避免碰撞的发生。此外，规划航迹还需要尽可能地降低能耗，以增加无人机执行任务的有效时间。无人机具备以下三种基本能力：感知、通讯和计算能力。感知能力是指无人机可通过机载传感器获知当前自身状态。通讯能力是指无人机间可实现全域通信，获取彼此信息。计算能力是指无人机可规划航迹。

2 基于MPC的多无人机协同航迹规划方法

2.1 求解框架

基于MPC的多无人机分布式时空协同航迹规划框架如图1所示。该结构运行于无人机平台上，平台由3个部分组成：MPC控制器、空间协同模块和时间协同模块。无人机在每一个通讯周期对外广播自身预测的航迹信息和最早/最晚到达时间。同时，无人机接收其他无人机预测航迹信息和预测最早/最晚到达时间。无人机平台的状态由机载感应设备获取。无人机平台在每一个采样时刻基于接收的预测航迹信息、预测最早/最晚到达时间和自身状态，在线规划航迹。

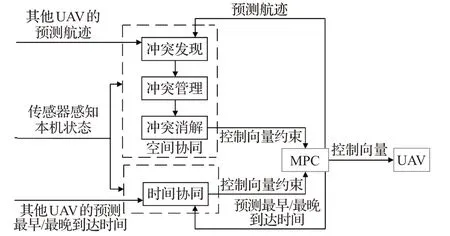
图1 基于MPC多无人机分布式时空协同航迹规划框架Fig.1 Structure of space-time cooperative path planning for multi-UAV based on MPC

MPC控制器根据本机和其他无人机状态、目标信息和控制向量约束等输入，对当前时刻的优化问题进行求解，输出控制时域内的控制向量，并应用控制向量的第一项对无人机进行控制操作。同时，无人机预测下一时刻的航迹和最早/最晚到达时间。

空间协同模块负责发现、管理和消除碰撞冲突。该模块按照功能属性又分为3个子模块[8]：冲突发现、冲突管理和冲突消解。冲突发现模块接收其他无人机的预测航迹，并与自身MPC控制器输出的本机预测航迹进行分析，生成预测冲突集合。冲突管理模块根据无人机获取的本机状态和预测冲突集合，对预测冲突集内的冲突进行管理和排序，并确定当前需要处理的冲突。冲突消解模块利用建立的碰撞消解规则，生成包括航向角和飞行速度在内的控制向量约束，并将其发送给MPC控制器。

时间协同模块负责无人机间的时间协同。该模块接收其他无人机预测的最早/最晚到达时间，结合无人机自身预测的最早/最晚到达时间，利用建立的时间冲突消解规则，生成飞行速度约束，并将其发送给MPC控制器。

2.2 MPC控制器

MPC是一种在线优化的控制策略。在每个采样时刻，它根据当前状态、参考信息和预测信息，通过求解一个优化问题，得到一个控制序列，并将该控制序列的第一个控制量作用于被控制对象。在下一个采样时刻，重复以上过程，从而形成闭环控制。MPC结构如图2所示[15]。

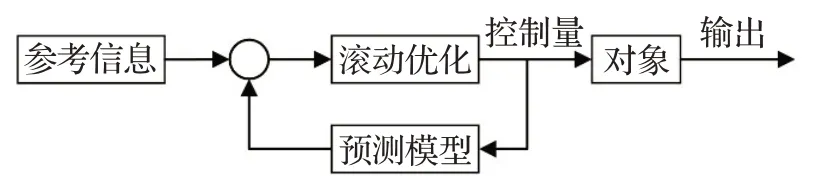
图2 MPC原理图Fig.2 MPC schematic diagram

由于每一架无人机具备独立的感知、通信和计算能力，因此在时空协同过程中，无人机可分别规划各自航迹，故采用分布式的结构进行控制。基于MPC框架的无人机时空协同航迹规划需要解决两个关键问题：预测模型和滚动优化。

2.2.1 运动模型

记无人机编队集合V={i|i=1,2,…,NV}，其中NV代表无人机的数目；并记Ui为第i架无人机。假设所有无人机均在水平面飞行，并将无人机视作平面内的一个质点。那么，其质点运动模型可表示如下[15]：

其中，xi(t)=[xi(t),yi(t),φi(t)]T表示Ui的状态向量，[xi(t),yi(t)]T∈R2表示Ui的位置，φi(t)∈[0,2π)表示Ui的航向角（以正北方向为零，逆时针方向正）。ui(t)=[vi(t),ωi(t)]T表示Ui的控制向量，vi(t)∈R表示Ui的速度，ωi(t)∈R表示Ui角速度。

对公式（1）进行离散化处理：设采样周期为δ，在第k个采样时刻，无人机的状态量和控制量的离散值记为。在采样时间周期内，和和，则无人机的离散化运动方程可表示为[15]：

以向量的形式重写公式（2）：

其中，yi(k+1)表示无人机输出向量，矩阵Aik、Bik和Cik分别为：

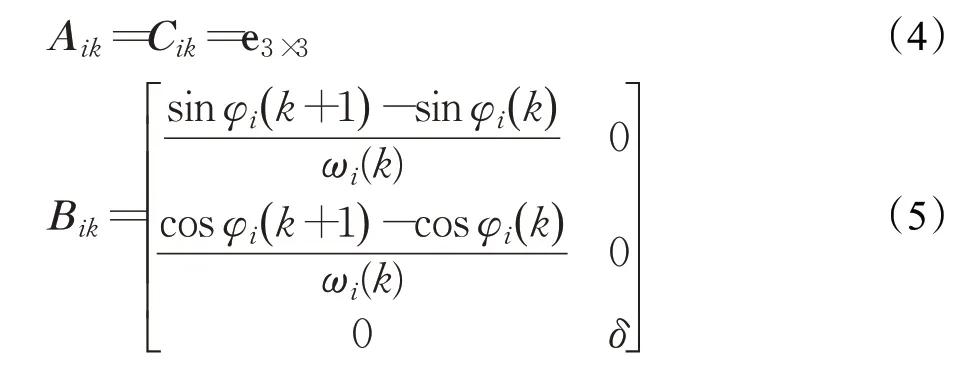
2.2.2 模型预测

（1）状态预测

假设不考虑干扰和测量噪声对无人机的影响，控制时域和预测时域分别设置为Nc和Np，并且满足Nc≤Np。由公式（2）和公式（3）可得到总的模型预测方程（公式（6））和输出预测方程（公式（7））[15]：

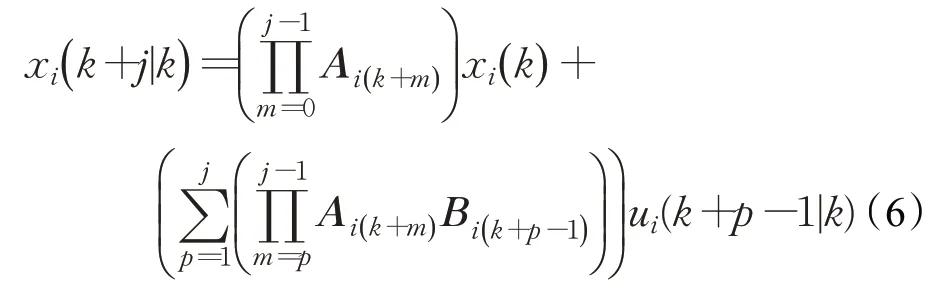
其中，j=1,2,…,Np。当Nc＜j≤Np，ui(k+j-1|k)=ui(k+Nc-1|k)。

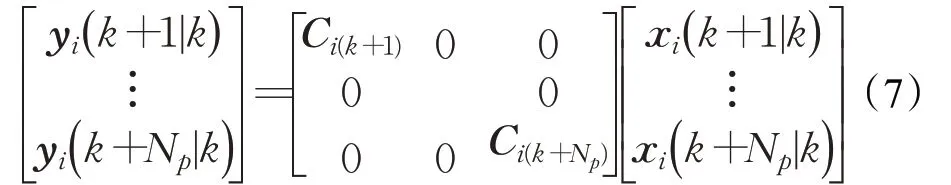
（2）最早/最晚到达时间预测

假设在第k个采样时刻，Ui距离目标的预测距离为Li(k)。Li(k)可按照下式估计：

2.2.3 滚动优化

滚动优化的关键是建立优化问题模型。在时空协同过程中，规划航迹除了满足时空协同的要求外，还需要尽可能地降低无人机能耗，缩短飞行距离，以增加无人机执行任务的有效时间。

（1）目标函数

在第k个采样时刻，Ui到目标的距离可表示为：

在一个时间周期内，Ui最大飞行距离可表示为：，其中表示Ui最大飞行速度。由公式（6）可计算Ui新位置xi(k+Nc|k)，新位置到目标的距离可表示为：

显然，d2越小Ui越接近目标。对d2进行归一化处理，得到如下目标函数：

（2）约束条件

①无人机性能约束

②时空冲突消解控制约束

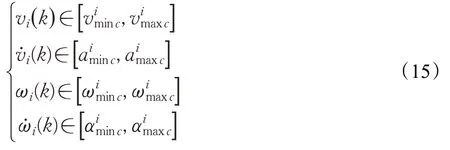
③空间协同距离约束

空间协同距离约束要求无人机在执行任务的过程中，任意时刻任意2架无人机之间的距离必须大于安全距离ds。假设为Ui第k步预测的t时刻的自身位置，为Ui接收到邻居Uj第k步预测的t时刻的位置，t∈(tk,tk+Npδ]，则有距离约束：

④时间协同约束

本文研究同时到达约束，对于Ui，同时到达约束可表示为：

其中，O(Ui)表示与Ui同时到达目标的无人机的序号集合。ts为满足同时到达目标要求的最大允许时间偏差。

2.3 空间协同模块

空间协同模块由冲突发现模块、冲突管理模块和冲突消解模块三个子模块组成。

2.3.1 冲突发现

冲突发现的目的是生成冲突集合，算法1给出了生成冲突集的过程。ds和de分别表示最小间隔距离（安全距离）和信息交互距离。第2～6行生成Ui的邻居集合：对于Ui，在每个采样时刻tk，当Ui与Uj之间的距离小于或等于de时，序号j加入到Ui的邻居集合Vi(tk)。第7～14行生成冲突集合：对于Ui，如果Ui与Uj(j∈Vi(tk))在预测航迹上的距离小于或等于ds，表示存在一个潜在冲突。潜在冲突是一个二元组，由入侵无人机序号和冲突时间共同组成。

算法1生成Ui的冲突集

Input：最小间隔距离ds；交互距离de；无人机序号集合V；离散化采样时间间隔δ；预测时域Np

Output：冲突集Ci(tk)

2.3.2 冲突管理

在预测时域内，当前无人机可能与多架无人机存在碰撞冲突。为了保证冲突处理的一致性，采用多碰撞优先级排序思想[8]对冲突进行管理。算法2实现了该过程。第2、3行，对冲突集Ci(tk)按照冲突发生时间升序排序。第4行，冲突集Ci(tk)中第一个元素作为待处理冲突，并标记待处理冲突的入侵无人机序号。第6～14行，按照速度大小和无人机编号的先后关系确定Ui与Up之间的leader-follower关系。

算法2确定leader无人机和follower无人机

Input：冲突集Ci(tk)，无人机速度v

Output：leadi和followeri

2.3.3 冲突消解

按照无人机的航向关系，冲突可分为两种：相向冲突和同向冲突。相向冲突是指2架无人机相向而行发生的冲突，如图3所示。同向冲突是指2架无人机同向飞行，后面的无人机由于速度较快，迫近前面的无人机，从而产生的冲突，如图4所示。

图4 同向冲突Fig.4 Chasing collision conflict diagram

为了消解两架无人机之间的冲突，文献[8]提出了航向规则和速度规则。然而，文献[8]仅提出了相向冲突的消解规则，没有给出同向冲突的消解规则。当使用文献[8]中规则解决同向冲突时，规则不能发挥有效作用，甚至可能导致碰撞的发生。本文在实验中，将用实例进一步说明此种情况。针对以上存在的问题，补充了以下同向冲突消解规则。设φL和φF分别代表leader和follower的航向角，0≤φL＜2π，0≤φF＜2π。Δφ表示leader的航向到follower航向的顺时针角度，0≤Δφ＜2π。

对于相向冲突：

（1）当0≤Δφ≤π，增加φL和φF；

（2）当π＜Δφ＜2π，减小φL和φF。

对于同向冲突：

（1）当0≤Δφ≤π，减小φL，增加φF；

（2）当π＜Δφ＜2π，增加φL，减小φF。

ΔφF和ΔφL分别表示leader无人机和follower无人机的航向角控制增量。图5和图6分别图解了相向冲突和同向冲突的航向角规则。图中的虚线箭头表示发生冲突的leader无人机和follower无人机的初始航向，实线表示按照冲突消解规则调整后的航向。

图5 消解相向冲突的航向规则Fig.5 Heading rules for opposite conflict

图6 消解同向冲突的航向规则Fig.6 Heading rules for chasing conflict

速度规则：增加leader无人机的速度，减小follower无人机的速度。

2.4 时间协同模块

记无人机编队中需要满足同时到达目标约束的无人机的集合为O。记，TL=。其中，和表示Ui预计最早和最晚到达目标时间。取TA=(TE+TL)2，TA表示集合O中的无人机期望到达时间。那么Ui在tk时刻的期望飞行速度为：。Li(k)为公式（8）计算得到的预测距离。那么，可建立以下时间冲突消解规则：

2.5 空间协同与时间协同解耦

由于空间协同和时间协同都需要调整无人机的控制向量，两个问题耦合在一起，相互影响，不方便处理。考虑到无人机飞行过程中避碰的重要性和偶发性，提出优先级的方法对空间协同和时间协同进行解耦。规定空间协同的优先级高于时间协同优先级，也就是说，无人机在需要同时处理空间协同和时间协同时，优先处理空间协同，直到不存在潜在碰撞时，再处理时间协同。

综合以上分析，给出基于DMPC思想的无人机时空协同航迹规划流程图，如图7。

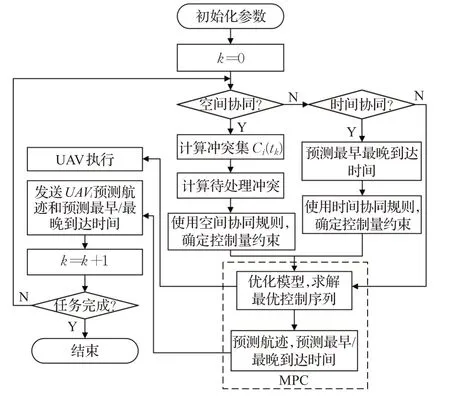
图7 多无人机时空协同航迹规划流程图Fig.7 Structure of space-time cooperative path planningfor multi-UAV

在采样时刻tk，Ui通过信息交互获取其他无人机预测信息，通过机内传感器获取当前状态信息xi(tk)，判断当前是否需要进行空间协同。若需要，利用空间协同单元确定Ui控制量（角速度和飞行速度）约束。若不需要，接着判断是否需要进行时间协同。若需要，利用时间协同单元确定Ui控制量（飞行速度）约束。然后，将xi(tk)、控制量约束、Ui的性能约束输入到MPC控制器，MPC调用DDECS算法[21]求解优化问题，生成Ui的控制序列ui(tk)。接着，对Ui应用ui(tk)中的第一项。更新状态信息xi(tk+1)，并基于xi(tk+1)和ui(tk)，对未来的航迹和最早/最晚到达时间进行预测。最后，将预测的航迹和预测的最早/最晚到达时间发送给其他无人机。重复以上过程，直至任务结束。

3 仿真实验

假设任务空域范围为50 km×50 km，无人机的最小速度为200 m/s，最大速度为300 m/s，最大角速度为10（°）/s，冲突发现距离de=8 km，安全飞行半径为ds=2 km，预测时域为20 s。无人机航迹规划的采样时间间隔δ=1 s。攻击发起距离设置1 km。最大允许时间偏差ts=5 s。DDECS算法的种群规模设置为20，最大函数评价次数设置为2 000，其他参数参考文献[21]。仿真实验环境：Intel Core i7-7500U 2.70 GHz、8 GB内存和64 bit Microsoft Windows 10。为了验证本文方法的有效性，选择3个无人机航迹规划场景进行仿真实验。

3.1 编码方式

本文采用无人机航向角的变化角度进行编码[22]。如图8所示，每个基因位上的αi(i=1,2,…,n)表示单位时长无人机航向角的变化值，因此采用实数编码方式。无人机以恒定的速度V飞行，按照规划的航向角完成机动，形成航迹S。具体来说，假设点是航迹S的起点，此时无人机的航向角为θ0。第一个基因位α1表示在单位时间Δt内，无人机的航向角改变了α1。那么无人机飞行Δt时长后的位置可以按照下式近似计算：

重复以上过程，可得到航迹上各点的坐标位置。

图8 编码方式示意图Fig.8 Schematic diagram of coding

3.2 2架无人机（相向冲突）航迹规划

2架无人机相向飞行，无人机的初始条件和仿真参数见表1。实验中，MPC单次循环最大耗时336 ms，平均耗时199 ms，可以满足δ=1 s条件下实时性要求。时空协同航迹规划仿真结果如图9（a）所示。

表1 实验1的初始条件和参数Table 1 Initial conditions and simulation parametersof experiment 1

依据初始条件，检测到潜在冲突（无人机1、2，11 s）。2架无人机按照航向角规则和速度规则，迅速调整航向角和飞行速度。图9（c）和9（d）展示了航向角和飞行速度的变化情况。图9（b）展示了2架无人机飞行过程中的相对距离。可以看出：在第26 s，2架无人机距离最小，相距2.26 km，满足空间协同的要求。2架无人机到达目标的时间均为107 s，时间差距小于5 s，满足时间协同的要求。而文献[8]规划得到的到达目标的时间分别是106和125，时间差距为19 s，大于5 s，不满足时间协同的要求。

图9 2架无人机（相向冲突）航迹规划仿真结果Fig.9 Path planning simulation results of 2 UAVs（opposite conflict）

3.3 2架无人机（同向冲突）航迹规划

2架无人机向同一方向飞行，无人机的初始条件和仿真参数见表2。实验中，MPC的单次循环最大耗时179 ms，平均耗时151 ms，可以满足δ=1 s条件下实时性要求。时空协同航迹规划仿真结果如图10（a）所示。

依据初始条件，检测到潜在冲突（无人机1、2，3 s）。2架无人机按照航向角规则和速度规则，调整航向角和速度。图10（c）和10（d）展示了航向角和飞行速度的变化情况。图10（b）展示了2架无人机飞行过程中的相对距离。可以看出：在第47 s，2架无人机距离最小，相距2.30 km，满足空间协同的要求。2架无人机到达目标的时间均为70 s，时间差距小于5 s，满足时间协同的要求。

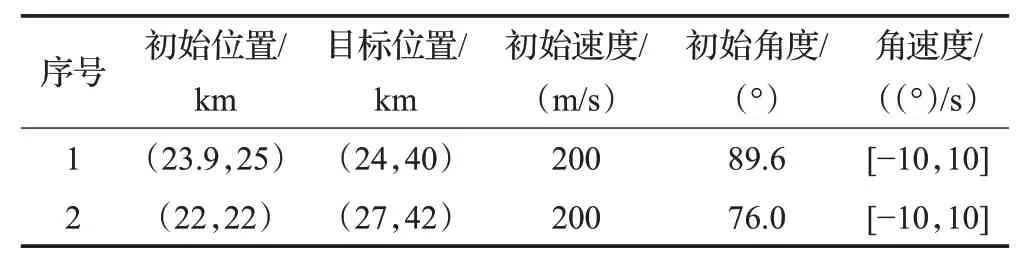
表2 实验2的初始条件和参数Table 2 Initial conditions and simulation parameters of experiment 2

本问题中的冲突属于同向冲突，若采用文献[8]中的方法，2架无人机将会相伴飞行，无法消解冲突（如图11所示）。并且在第11 s，无人机间的距离为1.97 km，将会发生碰撞。

3.4 4架无人机航迹规划

4架无人机同时执行任务，无人机的初始条件和仿真参数见表3。实验中，MPC单次循环最大耗时692 ms，平均耗时为530 ms，满足δ=1 s条件下实时性要求。时空协同航迹规划仿真结果如图12（a）所示。

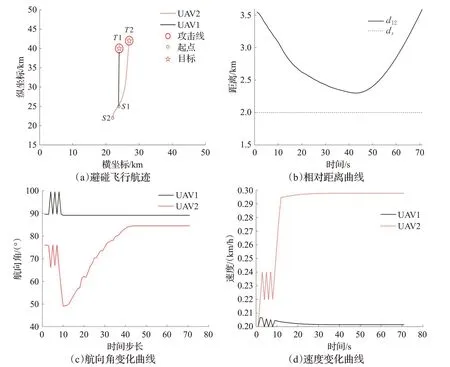
图10 2架无人机（同向冲突）航迹规划仿真结果Fig.10 Path Planning simulation results of 2 UAVs（chasing conflict）

图11 采用文献[8]冲突消解规则的仿真结果Fig.11 Simulation results with conflict resolution rules in Ref[8]

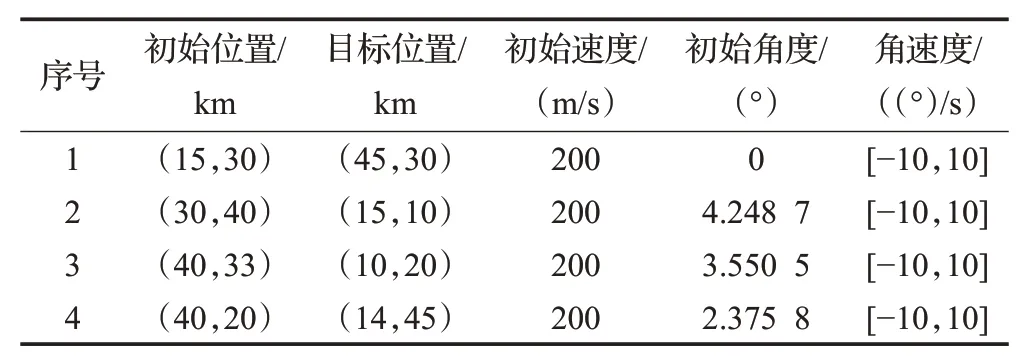
表3 实验3的初始条件和参数Table 3 Initial conditions and simulation parameters of experiment 3

依据初始的条件，检测到潜在冲突（无人机3、4，19 s）、（无人机1、2，26 s）和（无人机1、4，45 s）共3组。运用规则，调整航向角和速度。图12（c）和图12（d）展示了航向角和飞行速度的变化情况。图12（b）展示任意2架无人机的相对距离。可以看出：在第42 s，无人机1与无人机2间距离最小，距离2.33 km，满足空间协同的要求。4架无人机到达目标的时间均为136 s，最大时间差距小于5 s，满足时间协同的要求。文献[8]规划得到的到达时间分别为T1=134 s，T2=167 s，T3=162 s和T4=176 s，最大时间差距42 s，远大于5 s，不满足时间协同的要求。

4 结束语

本文提出了一种基于DMPC的同时处理空间协同和时间协同的在线航迹规划问题的方法。设计了由MPC控制器、空间协同模块和时间协同模块组成的多无人机分布式时空协同航迹规划框架结构。该算法的优点主要有三点：（1）通过对空间协同问题和同时到达问题设定不同的优先级，实现两种问题的解耦，从而可同时处理避碰问题和同时到达问题；（2）分析了以往航向规则的不足，提出了同向冲突的解决规则；（3）设计了时间冲突消解规则。最后，通过实验验证了本文提出的算法的有效性。未来，一方面将研究通信时延和时变通信拓扑条件下的多无人机协同航迹规划；另一方面，将研究多个优化目标的多无人机协同航迹规划问题。

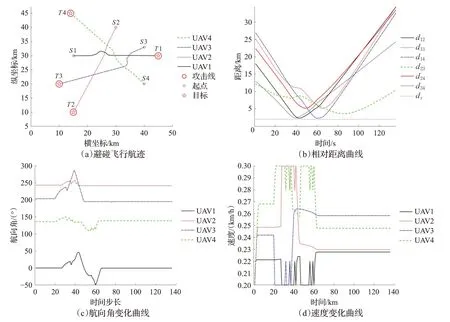
图12 4架无人机时空协同航迹规划仿真结果Fig.12 Path planningsimulation results of 4 UAVs