深度强化学习算法求解作业车间调度问题

李宝帅，叶春明

上海理工大学 管理学院，上海 200093

作业车间调度问题是常见的调度问题之一，其目标是在一定约束条件下对工件和机器按时间进行分配并安排加工次序，使得加工性能指标达到最优。针对作业车间调度问题的求解，有精确算法与近似求解算法可用于求解。精确算法如分支定界法、线性规划法等，但其局限性是在大规模调度问题上无法适用。近似求解算法可分为启发式算法与元启发式算法，可在短时间内获得调度问题的较优解。张腾飞等[1]利用改变初始解的生成方式、对染色体进行分段编码以及使用交叉算子等措施对遗传算法进行改进，并在标准算例上验证了改进遗传算法在柔性车间调度问题上的高效性；刘洪铭等[2]通过对粒子群算法中惯性系数、参数因子以及初始群生成方式进行改进，求解以机器加工时间最短为目标的车间调度问题。启发式方法，即调度规则也适用于解决调度问题，Panwalkar等[3]对调度规则进行了研究，系统总结了共113种调度规则，并对每条调度规则进行了相应描述；Mouelhi-Chibani等[4]利用小规模问题训练神经网络，根据系统状态实时选择两种调度规则进行调度，实验结果证明优于单一静态的调度规则选取方法。

强化学习算法拥有自决策的特点，可根据生产状态进行策略调整。Riedmiller等[5]首先利用强化学习对车间调度问题进行研究，利用强化学习方法，每个智能体对应每个机器，使用Q-learning算法学习车间中的调度策略以减少总拖延时间，在单一案例和多重案例上验证了算法有效性和泛化性；Aydin等[6]提出一种基于强化学习的动态调度系统，通过改进Q-learning算法，训练智能体根据车间状态变化选择当前最优的调度规则，在仿真系统中与单一调度规则进行对比，体现了算法优越性；Wang等[7]针对车间调度问题，利用Q-learning训练一个单机调度系统，选择三个调度规则来最小平均延误时间；Wang[8]基于强化学习方法，提出一种聚类与自适应调度策略的加权Q-learning来解决动态调度问题；张东阳等[9]针对置换流水车间调度问题，利用Q-learning算法引入状态变量与动作变量，将调度问题映射到强化学习问题中，算法在标准算例上表现优异。

但长期以来，强化学习的应用受限于问题规模解决问题本质上的低维度性，无法解决大规模问题与高维度问题，深度神经网络的融入解决了这一难题。Mnih等[10-11]提出了深度Q网络（Deep Q Network，DQN），使用神经网络拟合值函数，设置独立的目标网络以及经验回放机制，用于多款游戏的训练，并在多个游戏中击败了专业人类玩家。此后深度强化学习算法快速发展，同样应用于车间调度领域，肖鹏飞等[12]利用改进的DQN算法，通过定义状态空间、动作空间和奖惩函数，把调度问题转换为多阶段决策问题，将机器实时加工状态作为数据特征作为输入，输出最优生产周期对应的调度规则组合，解决以最大完成时间为目标的非置换流水车间调度问题，在标准问题上验证了有效性；Liu等[13]提出一种异步更新和深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG）的并行算法解决作业车间调度问题，采用多个智能体，将状态空间表示为三矩阵形式，设置调度规则集为动作空间，对调度问题进行了转换与研究；Luo[14]利用深度双Q网络[15]（Double DQN）算法研究了柔性车间调度问题，将柔性车间调度问题视为马尔可夫决策过程，设计七个状态特征表示生产状态，提出了六种复合调度规则作为动作空间，与Q-learning算法、多个调度规则在实例问题上进行对比，体现了算法的优越性与通用性；Yang等[16]利用DQN及DDQN算法以总延误为目标，研究了新作业到达下的动态置换流水作业调度问题，分别设计五种状态特征作为状态空间，五个调度规则作为动作空间，与元启发式算法在调度问题上进行对比，验证了算法的优越性。

综上所述，已有将DQN及其变体应用于调度问题的研究，本文利用DQN的改进版本，即DDQN与竞争网络架构的DQN算法[17]（Dueling DQN）结合而成的D3QN（Double Deep Q-Learning Network with Dueling Architecture）解决作业车间调度问题。D3QN算法对DQN进行改进，算法使用两个Q网络进行学习，实现动作选择与动作状态值函数的解耦，解决了DQN过高的值函数估计[18]，并且利用竞争网络模型代替DQN算法中的网络模型，可以解决奖励偏见问题，学习到更真实的价值函数。本文创新点在于通过定义状态空间、动作空间和奖惩函数将调度问题转化为一系列序列决策过程，利用D3QN算法对车间调度问题进行研究。在标准算例上与智能优化算法的实验结果对比验证了算法的有效性，同时算法原理上基于神经网络与强化学习，也适用于解决动态调度问题。

1 基本原理

1.1 强化学习

强化学习（Reinforcement Learning，RL）是机器学习的重要分支之一[19]。RL的本质是互动学习，目标是使智能体在与环境的交互过程中获得最大的累计奖励值，从而学得对自身动作的最优控制。RL的数学基础理论基于马尔可夫决策过程（Markov Decision Processes，MDP）。

1.1.1 马尔可夫决策过程

马尔可夫性质（Markov Property）指的是系统的下一个状态只与目前状态有关，而与之前的所有状态都不相关。如果一个系统具有马尔可夫性质，则可根据当前状态与动作预测未来状态和奖励[20]，马尔可夫性质使得马尔可夫决策过程易于表示，满足马尔可夫性质的RL任务称为MDP[21]，具体而言，一个马尔可夫决策过程可由一个四元组组成，即MDP=(S,A,Psa,R)。S为状态空间集合，A为动作空间集合，Psa为状态转移概率，表示在当前状态下执行动作后转移到另一个状态的概率，R为奖励函数。

1.1.2 强化学习求解

在RL中，智能体从环境中不断采样，最终目标是学习到一个最优动作策略π*，即在任意时间步中执行动作a所得到的累计奖励R最大。在实际应用中，通常用折扣未来奖励累计奖励G1来表示时间步t内的未来累计奖励，即：

其中γ是折扣因子。状态值函数v(s)是表示在状态s下执行动作a得到的奖励期望：

动作值函数q(s,a)是评估当前智能体在状态s下选择动作a的好坏程度：

最优值函数是在每一个状态上，其值大于其他值函数在该状态的值的值函数，即：

值函数的贝尔曼方程为：

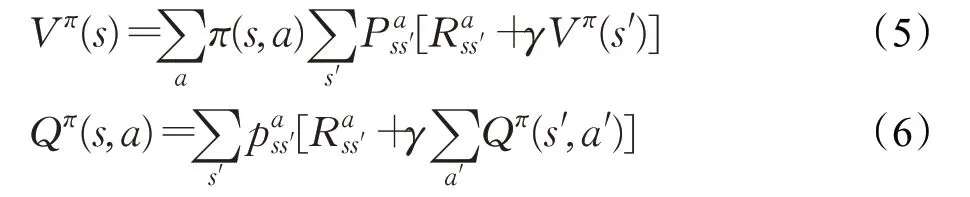
基于式（3）、（4）、（5），可以得到最优贝尔曼方程：

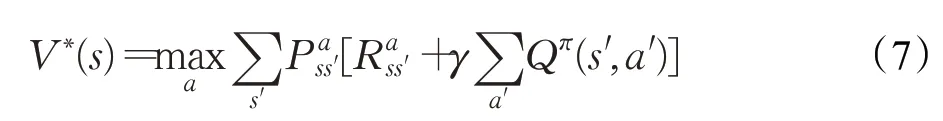
1.2 深度学习

深度学习是一种有监督的学习方法，使用神经网络对原始数据特征进行多步特征转换，不断对原始数据中的特征进行表征，最终得到可表示数据本质特征的高维抽象特征[22]。目前，深度学习采用的模型主要是神经网络模型。

1.2.1 深度神经网络

深度学习的核心是深度神经网络，神经网络可看作非线性模型，其基本组成单位时具有非线性激活函数的神经元，通过大量神经元的连接，神经网络成为非线性的模型。如图1所示是神经元与多层前馈神经网络结构示意图。

图1 神经元与多层前馈神经网络结构图Fig.1 Neuron and multi-layer feedforward neural network structure

神经元由连接、求和节点和激活函数构成，其实现了对输入数据的非线性变化。多层前馈神经网络一般由多个网络层组成，每层网络层都由多个神经元构成。深度学习首先通过对有标签数据的训练得到网络模型，之后进入预测阶段，新数据输入网络模型，最后得到新数据的预测结果。

1.2.2 神经网络优化方法

神经网络优化目标是找到更好的局部最小值及提高优化效率，其改善方法可分为以下几类：

（1）使用更有效的优化算法来提高梯度下降的效率和稳定性，如使用学习率衰减、周期学习率调整等自适应调整学习率方法；使用动量法、Adam算法对梯度估计进行修正。

（2）改进参数初始化方法。参数设置在神经网络中非常关键，可使用随机初始化方法，如正交初始化方法、基于方差缩放的初始化方法来提高神经网络的训练效果。

（3）修改神经网络模型，比如使用逐层归一化，Relu激活函数以及残差链接等。

2 深度强化学习方法

2.1 调度问题的转换

利用深度强化学习方法研究车间调度问题，首先需进行车间调度问题向马尔可夫决策过程的转化，使得调度问题可以得到较好的表示与解决，首先需要适当定义车间调度问题中的状态空间、动作空间与奖惩函数。

2.1.1 状态空间

状态空间是调度过程中所有状态的集合，为了充分表示调度过程中的状态变化，状态空间的表示应该遵循以下原则：

状态特征可描述调度环境的主要特征和变化；状态特征的选择应该与调度目标相关，否则会造成特征冗余；不同调度问题的所有状态都用一个共同的特征集来表示；状态特征是对状态属性的数值表示，状态特征应易于计算与表示。

本文采用文献[23]的方法，将状态特征表示为三个矩阵的形式，第一个矩阵为各工件每个工序的处理时间所组成的矩阵，第二个矩阵为当前时间步长的调度结果组成的矩阵，第三个矩阵为机器利用率组成的矩阵。以一个3×3的调度例子说明，如图2所示为前三个工序的调度过程与状态空间矩阵的转化，在初始状态，处理时间矩阵里面每个值都是工序的加工时间，调度结果矩阵与机器利用率矩阵都为零，当前三个工序加工完成时，处理时间矩阵中已完成的工序转换为零，调度结果矩阵转换已完成的工序，机器利用率矩阵也进行相应的转换。

图2 状态空间矩阵转化情况图Fig.2 State space matrix transformation

2.1.2 动作空间

动作空间为智能体在当前状态下可采取动作的集合。在调度问题中，智能体执行的动作是根据调度规则选择优先加工的作业，动作空间的选取为启发式行为，为避免单一规则的短视性，选择多个与最大完工时间相关的调度规则作为动作空间。为了更好地确定调度规则，选取的调度规则要尽可能多样化，调度规则本身可以与调度目标相关，也可以不相关，选择多样化的调度规则来充分发挥智能体从经验中学习的能力。本文共选取了20个调度规则，如表1所示。

表1 调度规则Table 1 Scheduling rules

应用基于矩阵形式的状态空间与以调度规则为动作空间的调度转化方法，适应深度强化学习算法要求，根据生产状态的变化选取调度规则，可以充分发挥算法的自主决策与优化能力。相较于元启发式算法传统的两段式编码解码方法，更能体现机器与加工工件在加工过程中的变化，更贴近实际生产状态的变化。

2.1.3 奖励函数

奖励函数选取适当与否与深度强化学习效果相关，短期奖励可以看作是每个动作的短期回报，也代表该动作对调度方案的短期影响。累计奖励反应的是每个动作产生的奖励总和，深度强化学习的最终目标就是最大化累计奖励。

本文的调度目标是最小最大完工时间，这一目标可通过最大加工机器利用率来进行转换，因此使用平均机器利用率来表示机器加工的利用率，平均机器利用率可以表示为：

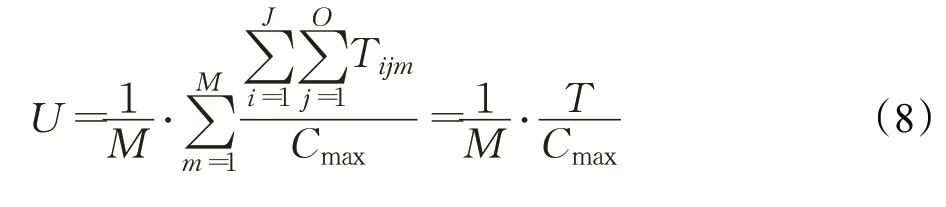
U为平均机器利用率，M为机器数，Cmax为最大完工时间，Tijm是机器加工工件某工序所需时间。令R=U，则奖励函数可以表示为：

2.2 D3QN算法

D3QN算法以DQN算法为基础，结合了Double DQN与Dueling DQN。Double DQN可解决DQN过高的值函数估计问题，由于DQN算法在根据下一时间步的状态选择动作的过程中可能会选择过高的估计值，从而导致过高的值函数估计，因此Double DQN在计算目标Q值时使用两个不同的网络模型参数，使得动作的选择和动作的状态值估计解耦，进而可避免过高的值函数估计。Dueling DQN对DQN网络架构进行修改，大幅提升了学习效果，如图3所示，Dueling DQN对于DQN的改进在于全连接层，将全连接层改为两个流，一条输出关于价值的函数，另一条输出关于动作的优势函数的值，二者结合成价值函数，智能体可学习到在没有动作影响下更真实的价值函数。

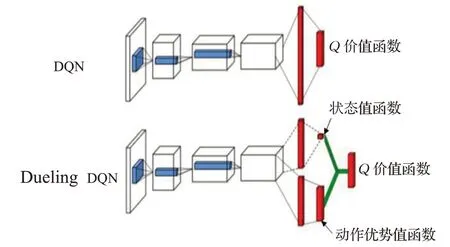
图3 Dueling DQN与DQN网络架构对比图Fig.3 Dueling DQN versus DQN network architecture

2.2.1 探索与利用

探索的目的是找到更多有关环境的信息，而利用的目的是利用已知的环境信息来最大限度地提高奖励。在算法尝试次数有限的前提下，探索和利用两者本身是矛盾的，增加探索的次数就会降低利用的次数，反之亦然，因此必须平衡探索与利用的次数，以达到最大累计奖励。本文使用ε-贪婪算法来实现智能体的探索与利用，ε-贪婪算法的数学表达式为：

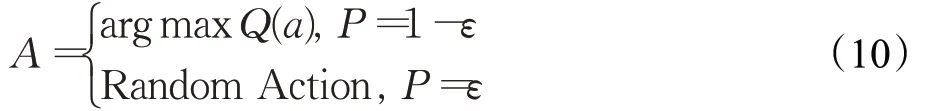
P=ε表示算法以ε的概率选择动作空间的动作，P=1-ε表示算法以1-ε的概率选择当前时间步内价值最大的动作作为下个时间步要执行的动作。

2.2.2 算法流程与实施

本文利用结合DDQN与Dueling DQN算法的D3QN算法应用于作业车间调度问题，D3QN算法框架如下：

（1）初始化复用池D的容量为N；初始化动作值函数Q，设置随机权重θ；初始化目标动作值网络Q̑，权重参数为θ-=θ。

（2）forepisode=1，Mdo；初始化序列以及第一个对状态的预处理序列。

（3）fort=1，Tdo；以ε的概率随机选择一个动作at否则选择。

（4）在调度环境中执行动作at并安排优先级最高的工件，将完成的工序从第一个矩阵中删除并加入到第二个矩阵中。

（5）观察奖励ri和下一个状态st+1；下一个状态st+1=st,at,xi+1，下一个预处理序列ϕt+1=ϕ(st+1)。

（6）存储样本于经验复用池D中，随机抽取小批量样本(ϕj,aj,rj,ϕj+1)。

（7）计算每个样本的TD目标差，在(yt-Q(ϕj,aj;θ))2上执行梯度下降；每隔c步重设Q̑=Q。

算法共有两个循环，算法开始阶段，将一个调度实例的工序处理时间矩阵、调度结果矩阵以及机器利用率矩阵组成的三通道矩阵输入卷积神经网络，输出是单个动作的预测Q值。在episode开始时，调度方案被重置，获得初始状态s0，在t≤T时，智能体观察当前状态，根据ε-贪婪策略执行一个动作，在动作执行以后，具有最高优先级的工件进行处理，完成的工序会从工件工序处理时间矩阵中删除，剩余的工序仍然保存在当前时间步长处理结果矩阵中。之后智能体得到奖励r1并观察下一个状态st+1，并将序列(ϕt,at,rt,ϕt+1)存入经验复用池。当经验复用池中存储了足够多的样本后，从其中随机取出小批量样本，计算每个样本的TD差，之后对θ执行梯度下降法求解，每隔c步重设Q̑=Q。算法流程如图4所示。

3 实例验证

3.1 模型与参数设置

本文应用算法为Dueling Double DQN（D3QN），基于Python语言与Tensorflow2.0框架实现，配置Intel Core i5-9300H CPU＠2.40 GHz，RAM 16 GB。在D3QN中，第一层为状态空间输入层，之后连接三个卷积层，在进行卷积操作后，将提取的特征分流竞争网络层，竞争网络层包括两个支路，价值网络和优势动作网络，二者都是完全连接的，价值网络只有一个输出，动作优势网络的输出与动作空间一样多，二者最终汇合到一起得Q值，卷积层激活函数选用Relu，算法模型结构如图5所示。

参数设置对于算法的表现具有较大影响，但参数范围较广，难以确定合适参数，因此遵循一般的设置原则。部分参数设置如表2所示。

图4 算法流程图Fig.4 Algorithm process

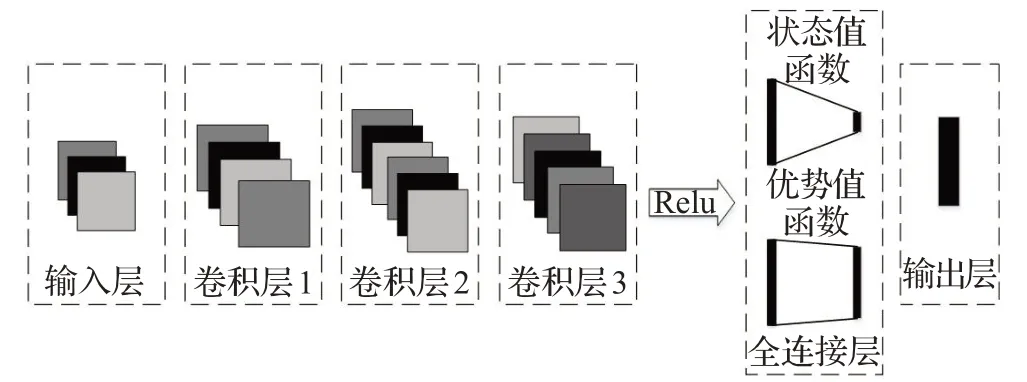
图5 算法模型结构图Fig.5 Algorithm model structure

表2 D3QN模型部分参数设置Table 2 Some parameter settings for D3QN model

3.2 算例实验与分析

为验证算法的有效性，对算法进行实例验证，选取的实例来源于已公开的FT、LA、SWV[23]基准测试实例。

本文选取最大完工时间为评价指标，算法的动作空间为调度规则，因此选用两个单一调度规则以及标准遗传算法、粒子群算法与本算法进行比较，算例实验对比情况如表3所示，其中最优调度结果以粗体显示。

表3 实验结果对比Table 3 Comparison of experimental results

分析表3可知，D3QN在标准算例上的表现明显优于单一调度规则，相较于标准遗传算法和粒子群算法，在小规模问题的表现上具有一定优势，虽在部分问题上也并未取得最优解，但在大规模问题的表现上明显较好。在面对大规模问题时，D3QN虽未在调度问题上取得最优解，但所求解的质量下降较为缓慢，且这一趋势会随着问题规模的增大而更为明显，这表明算法本身的适应度较好。由于算法使用Python语言及Tensorflow框架，算法时间对比并未列出，基于神经网络的算法在经过训练之后可以在较短时间内输出调度结果。图6、图7所示是D3QN对比粒子群算法、遗传算法在ft10与swv06算例上完工时间随迭代次数变化对比图。

图6 ft10最大完工时间迭代对比图Fig.6 ft10 maximum completion time iteration

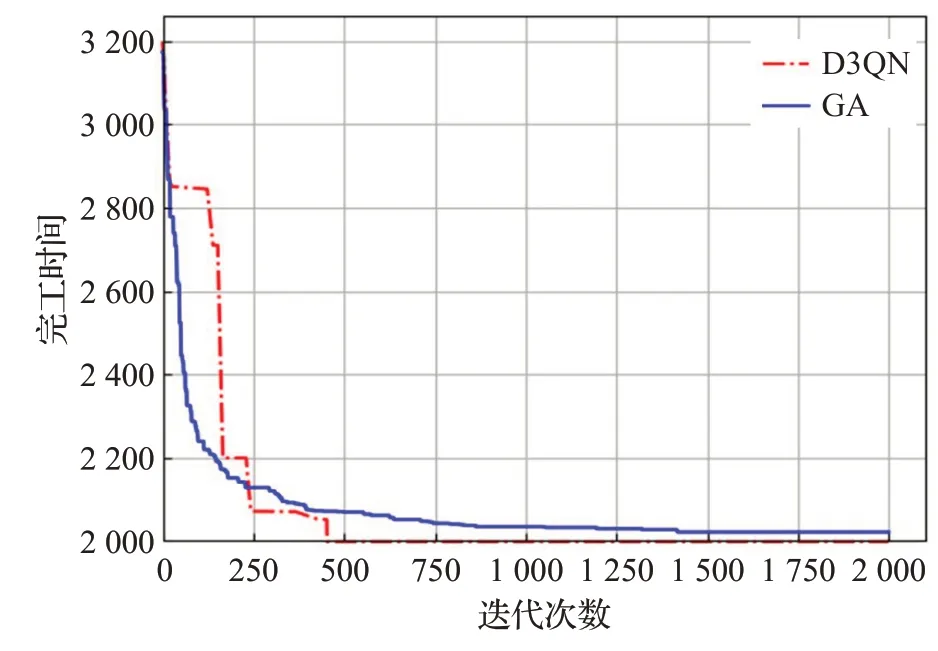
图7 swv06最大完工时间迭代对比图Fig.7 swv06 maximum completion time iteration

分析图6、图7可了解D3QN算法相较于PSO、GA在前期完工时间迭代下降较为缓慢，但在后期迭代过程中则会得到算例的较优值。

4 结束语

本文利用D3QN对作业车间调度问题进行研究，将调度问题转化为一个序列决策问题，用多通道图像来表示每个时间步的调度状态，使用启发式规则及组合作为动作空间，设置奖励函数，在标准算例的验证下，算法的调度效果优于单一调度规则与智能优化算法，总体上取得了较为可观的调度结果。

进一步的研究工作可以集中在以下几个方面，奖励函数的设置利用了两个连续时间步的机器利用率之差，将进一步研究更有效的设置方法来达到更好的效果；使用的D3QN算法模型本质上是基于价值的DRL方法，为进一步提升算法性能可考虑基于策略的DRL方法，例如AC、AC3等；研究问题集中于单一的作业车间调度问题，可进一步研究算法在多目标车间调度问题、动态调度问题其他复杂调度问题上的应用效果。