求解多目标路径优化问题的涟漪扩散算法

胡小兵，陈树念，张盈斐，谷升豪

1.中国民航大学 电子信息与自动化学院，天津 300300

2.中国民航大学 经济与管理学院，天津 300300

3.中国民航大学 中欧航空工程师学院，天津 300300

Pareto前沿是解决多目标优化问题（Multi-Objective Optimization Problem，MOOPs）的关键概念，它与一组Pareto最优解[1-4]相关。现有的MOOPs方法大多只能找到部分或近似的Pareto前沿，无法得出完整的Pareto前沿。现有的MOOPs方法主要分为三类：重构单目标函数法（Aggregate Objective Function，AOF）、约束目标函数法（Constrained Objective Function，COF）和Pareto标准评级法（Pareto-Compliant Ranking，PCR）。AOF和COF均是通过求解单目标优化问题（Single-Objective Optimization Problem，SOOP），得到原多目标优化问题的解[2，5-9]。其中AOF是将所有原始目标整合成一个单一的目标函数，而在COF中，只有一个目标函数被优化，而其他目标函数都被当作约束条件[10-12]。PCR是通过基于种群进化的各种进化算法（如遗传算法、粒子群算法和蚁群算法）和Pareto非占优解，生成一个候选解集，得到多个Pareto非占优解[13-20]。尽管这些方法被广泛应用于解决各种MOOPs，但通常很难判断它们是否找到了完整的Pareto前沿[11]并且很难证明所得到的离散MOOPs的近似Pareto前沿是否就是理论上的完整Pareto前沿[4]。

文献[21]介绍了一种在理论和实践上都能保证找到离散MOOPs的完整Pareto前沿的确定性方法，即涟漪扩散算法（Ripple-Spreading Algorithm，RSA）。简单来说，文献[21]中的RSA有两个重要步骤：第一步，找出MOOP的每个单目标函数的前k个单目标最优解，假设给定的MOOP有NObj个目标函数，那么就有NObj×k个单目标最优解；第二步，比较这NObj×k个单目标最优解，找出其中所有的Pareto非占优解，这些解将确定完整的Pareto前沿。该方法被成功应用于新产品开发项目管理[22]和灾害风险科学[23]中的一些多目标优化问题（MOOPs）的求解。

对于多目标路径优化问题（Multi-Objective Path Optimization Problem，MOPOP），已有研究证明，利用标号设置和标号校正等方法均能找到完整的Pareto前沿[24-27]。一般而言，这些方法都是针对单目标路径优化问题的Dijkstra算法和A*算法的拓展[25]。如文献[28-30]所示，RSA作为一种新型的、受自然启发的、基于多智体的确定性算法，在解决一些复杂的路径优化问题时，相对于传统的Dijkstra算法和A*算法有一定的优势。例如，当考虑具有时间窗或时变路径的路网时，RSA比Dijkstra算法和A*算法表现出更大的灵活性和更高的计算效率[29-30]。

文献[21]中求解MOPOP的方法的基本思想与RSA的涟漪扩散优化原理无关，文献[21]中所使用的RSA本身是一种单目标路径优化问题的求解方法。对于具有NObj个目标函数的MOOP，文献[21]中的RSA至少需要运行NObj次，本文在文献[28]所述的涟漪扩散优化原理的基础上，开发一种可以直接求解MOPOP的完整Pareto前沿的RSA。在这个新的RSA中，无需计算前k个单目标最优解，只需运行一次就可以得到一对多问题中每个MOPOP完整的Pareto前沿，并且具有理论最优性保障。假设路网有NN个节点，如果将文献[21]的方法应用于一对多问题的MOPOPs，需要将文献[21]的方法应用(NN-1)次，即文献[21]中的RSA需要运行至少(NN-1)×NObj次。而新的RSA只需运行一次，就可以解决同样的一对多问题中的所有MOPOPs。

1 MOPOPs的问题描述

假设一个路网G(V,E)由节点集V和链接集E组成。这个路网可以表示为一个NN×NN的邻接矩阵A，矩阵A(i,j)=1(i=1,2,…,NN;j=1,2,…,NN)表示从节点i到节点j的有向链接，当A(i,j)=0时表示不存在链接。假设A(i,i)=0，即不允许存在自连接链接。待优化的目标函数的个数为NObj，则Ck(i,j)(k=1,2,…,NObj)表示与链接A(i,j)相关的、用于计算第k个目标函数值的链接成本。

在一对一MOPOP中，一对起始点和终点表示为[S,D]，找出从S到D的所有Pareto最优路径方法如下：假设候选路径表示为整数向量p(i)=j，即节点j是路径p上第i个节点（i=1,2,…,NP；j=1,2,…,NN，NP表示节点个数，包含起始点和终点），p(1)=S，p(NP)=D。由于本研究中不允许出现循环路径，所以一个节点在一条路径中最多只能出现一次，即：

当i≠j(i=1,2,…,NP;j=1,2,…,NP)，

对于给定的路径p，根据每个目标函数计算从起始点到终点的总成本为：

其中fk是MOPOP的第k个目标函数。

则一对一MOPOP可表述为如下最小化问题：

其中p满足约束条件式（1），并且：

ΩP是连通[S,D]的所有的可能路径的集合。

上述问题的Pareto最优路径p*具有以下特点：不存在任何p可以使得：

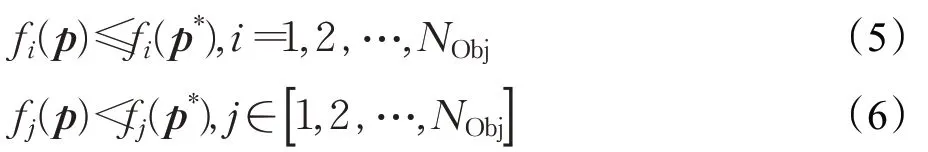
即路径p*不被任何其他路径p所Pareto占优。这样一个p*在目标函数空间里的投影叫做Pareto点。对于上述一对一MOPOP，通常存在一组Pareto最优路径，该集合在目标函数空间中的投影就称为Pareto前沿。

目前的大多数方法只能找到MOPOP部分或近似的Pareto前沿，无法确定完整的Pareto前沿。由图1可见，在双目标路径优化问题中，完整的Pareto前沿与部分、近似的Pareto前沿往往存在差异，如果给决策者提供一个部分、近似Pareto前沿，决策者将无从知晓是否还存在其他的Pareto最优方案（在图1中，用AOF/COF方法得到的部分Pareto前沿遗漏了最佳的折中解决方案），甚至无法确定提供解决方案的点确实为Pareto最优（在图1中，PCR方法得到的近似Pareto前沿实际上有4个假的Pareto点）。因此，使用部分或近似的Pareto前沿意味着决策者可能无法得到最想要的解决方案。显然，如果计算出完整的Pareto前沿，那么决策者在面对MOPOP时，就可以得到最全面的信息进行决策支持。

图1 近似Pareto前沿和完整Pareto前沿Fig.1 Examples of partial，approximated and completePareto fronts

一对多问题的MOPOP的数学描述可看作是NN-1个一对一MOPOP的总和，即对于给定的起始点S，以路网中的另外NN-1个节点中的任一节点作为终点，构造一个一对一MOPOP。因此，在一个一对多的MOPOP中，总共有NN-1个一对一的MOPOP。对每个一对一的MOPOP都要找出相应的完整Pareto前沿。因此，求解一对多的MOPOP需要计算NN-1个完整Pareto前沿。

2 求解MOPOP的RSA

2.1 RSA的基本思想

自然界中的涟漪扩散现象反映了一个优化原理：涟漪以相同的速度向四周扩散，总是最先到达最近的节点。这个简单的优化原理可以很容易地应用于有效求解路径优化问题（Path Optimization Problem，POP）。现有的路径优化方法大多是集中式、自上而下、基于逻辑的搜索算法，而RSA却是一种离散式、自下而上、基于多智体的仿真模型。一般而言，多智体模型具有以下显著特点：各个智体按某种规则各自独立行为，单个智体的行为一般不需要全局性的信息支持；所有智体各自独立的微观行为合在一起就自下而上地涌现出了模型和算法的某种宏观特性。在RSA中，各个涟漪和节点就是智体；每个涟漪的扩散行为和终止行为，以及每个节点的涟漪激活行为，都由特定规则决定，且各个智体的行为彼此独立（例如，两个涟漪可以同时扩散，但是这两个涟漪的扩散状态完全独立）；涟漪行为和节点行为不需要全局性的信息；各自独立的涟漪行为和节点行为最后涌现出RSA的宏观最优性保证（即无需全局信息的智体微观行为最后却能产生全局最优性的路径）。

RSA模拟了路网中的一次涟漪接力赛。涟漪从起始点开始扩散，当扩散到某一节点时，在一定条件下，该节点可能会触发新的涟漪；当涟漪到达其起始点的所有相邻节点时，涟漪将消失；所有存在的涟漪不断扩散，在空间上更远的节点处触发更多的涟漪；当满足终止条件时，接力赛结束。RSA由于是一种基于智体的模型，根据特定问题设计微观智体行为（即节点如何产生涟漪）和宏观终止条件（即涟漪接力赛何时结束），就可以有效地解决各种POPs以及任何可转化为POP的问题[28]。

2.2 针对MOPOP的RSA设计

2.2.1 一对一MOPOP的RSA设计

首先，为了找到第1章中定义的一对一MOPOP的可以保证理论最优性的完整Pareto前沿，定义了RSA新的微观智体行为和宏观终止条件。在针对MOPOP的RSA中，微观智体行为定义是：当某节点处刚到达的涟漪不被该节点处任何先前的Pareto非占优涟漪（Pareto Non-Dominated Ripples，PNDR）所Pareto占优时（公式（5）和公式（6）的条件），且涟漪接力赛没有结束，那么该节点将会触发新的涟漪。

基于一对给定的[S,D]的MOPOP的RSA，即一对一的MOPOP，描述如下：将涟漪r从起始点S到达节点n的NObj个路径成本与节点n上的每个PNDR的NObj个路径成本进行对比，如果涟漪r相对该节点上之前的PNDRs是Pareto非占优的，那么涟漪r就成为节点n上的一个新的PNDR。假设涟漪r∈ΩPNDR(n)（ΩPNDR(n)是在节点n上的PNDRs），Fi(r,n)表示基于第i(i=1,2,…,NObj)个目标函数的涟漪T(r)（T(r)表示产生涟漪r的涟漪）从S到达节点n的路径成本。则求解一对一MOPOP的完整Pareto前沿的RSA的步骤如下：

步骤1为同时保证最优性和高效性[28]，假设第h个目标函数在所有NObj个目标函数中具有最大值min(Ch(i,j))/max(Ch(i,j))，则设置涟漪扩散速度为：

步骤2令ΩPNDR(n)=∅,1≤n≤NN。在起始点S处产生第一个涟漪，并将当前涟漪数NR设置为NR=1。设E(NR)=S（E(r)表示在节点E(r)处产生涟漪r），R(NR)=0（R(r)表示涟漪r的半径），SR(NR)=1（SR(r)=0/1表示涟漪r处于非激活状态/激活状态），T(NR)=0（第一个涟漪为自触发）。让ΩPNDR(S)={NR}，并设置Fi(NR,S)=0，i=1,2,…,NObj。设置当前仿真时间t=0。

步骤3如果r=1,2,…,NR，都有SR(r)=0，即不会产生新的涟漪，或者如果对于任意SR(r)=1(1≤r≤NR)，涟漪r的当前路径成本已经被终点D已有的PNDRs的路径成本所Pareto占优，则转到步骤7。否则，转到步骤4。

步骤4令t=t+1。对于每一个涟漪r，即若SR(r)=1(1≤r≤NR)，则涟漪r的半径增加v，即：

步骤5对于任意节点n，如果至少存在一个1≤r≤NR，使 得SR(r)=1，而 且A(E(r),n)=1，R(r)≥Ch(E(r),n)，即涟漪r是一个到达节点n的涟漪。那么，先将所有到达节点n的涟漪（如果到达涟漪的数目超过1个）进行对比，再将到达涟漪与节点n上的当前PNDRs进行对比，找出其中的PNDR。节点n的每个到达涟漪（即涟漪r）将在节点n触发一个新的PNDR：令NR=NR+1；设E(NR)=n，T(NR)=r，R(NR)=R(r)-Ch(E(r),n)。当n≠D时，设SR(NR)=1；否则设SR(NR)=0，即在终点上触发的新涟漪不会扩散；ΩPNDR(n)=ΩPNDR(n)+{NR}；涟漪r从起始点S到达节点n的路径成本记录为Fi(NR,n)(i=1,2,…,NObj)。

步骤6对于扩散中的涟漪r（即SR(r)=1），对任意满足A(E(r),n)=1的节点n，如果都满足以下条件：

则令SR(r)=0，即涟漪消失。转到步骤3。

步骤7对终点D上的每个PNDR，即如果r∈ΩPNDR(D),1≤r≤NR。则[F1(r,D),F2(r,D),…,FnObj(r,D)]就是一个Pareto点，涟漪r从S到D的旅行路径就是一个Pareto最优解。D上的所有PNDRs就确定了完整的Pareto前沿和所有的Pareto最优路径。

图2给出了一个RSA求解一对一MOPOP的示例。RSA的涟漪接力赛从S处的涟漪R1开始，在时刻1到2的时段内，R1依次到达节点2、1、3，R1为节点2、1、3上的第一个PNDR，并在节点上触发新的涟漪（即R2、R3和R4）。然后R1消失，因为它已经到达了S的所有相邻节点。

在时刻2到3的时段内，R2到达终点D，成为D处的第一个PNDR，所以路径S-2-D为一条Pareto最优路径。R3到达节点2，将R3到达节点2时的目标函数值和R1到达节点2时的目标函数值进行对比，由于R3不被R1占优，因此R3成为节点2处的第二个PNDR，并在节点2处触发新的涟漪R5。虽然R2在时刻2到3的时段内到达节点1，但是R2被R1占优（R1是节点1的第一个PNDR），因此R2不能在节点1触发新的涟漪。

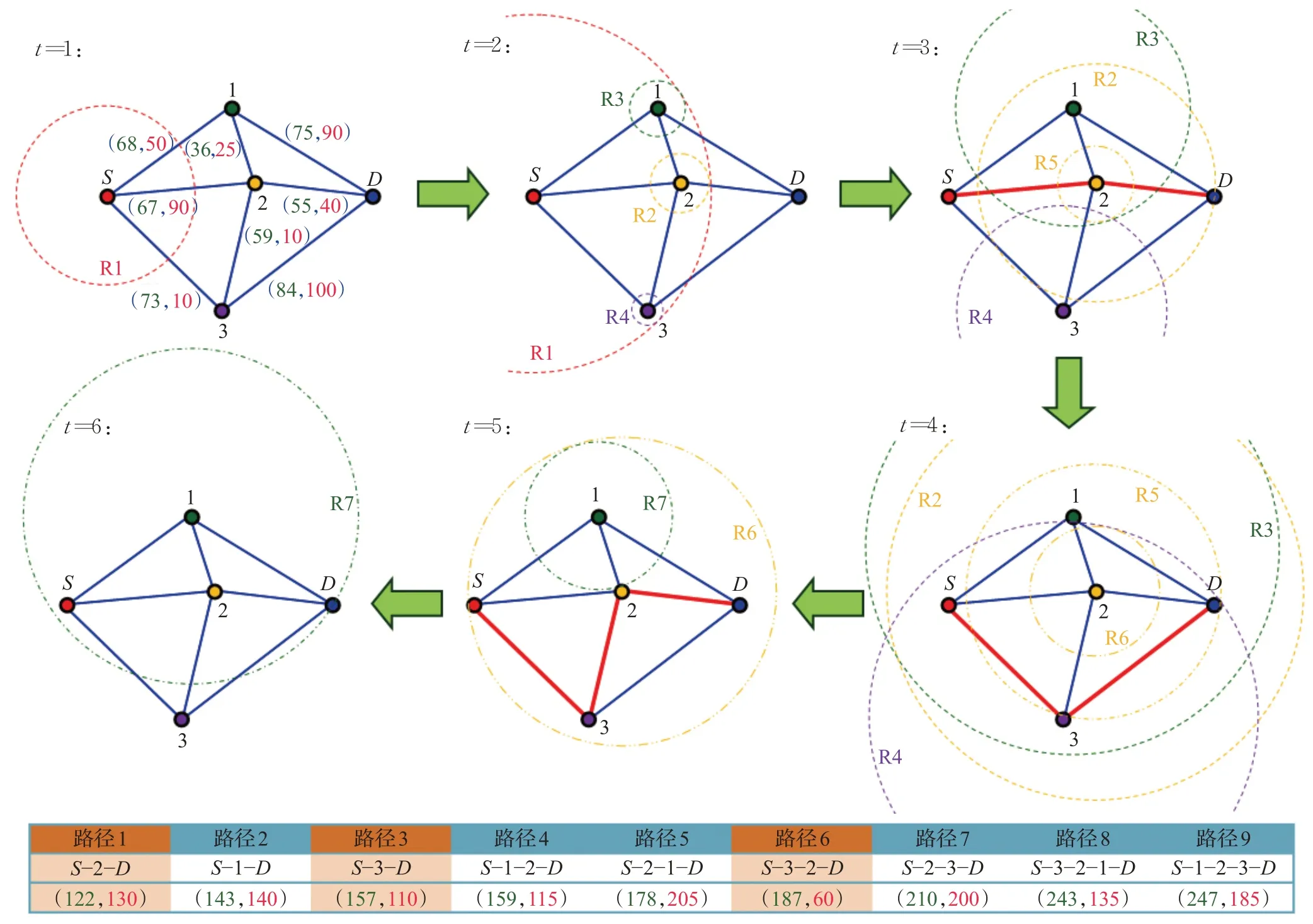
图2 RSA确定一对一MOPOP的完整Pareto前沿的示例Fig.2 Illustration about how complete Pareto front is identified for one-to-one MOPOP by RSA

在时刻3到4的时段内，R3先到达D，但由于R3被R2（D处的第一个PNDR）占优，所以R3没有确定新的Pareto最优路径；R4跟随R3到达D，成为D处的第二个PNDR，因此确定路径S-3-D为另一条Pareto最优路径；R5跟随R4到达D，但被R4占优；R4也到达节点2，由于在节点2上R4不被任何之前的PNDR占优（即R1、R3），所以R4成为节点2的第三个PNDR，并在节点2处触发涟漪R6；R2到达节点3，但被节点3的第一个PNDR（即R1）占优。

在时刻4到5的时段内，R6到达D，因为R6在节点D处不被之前的PNDR占优（即R2和R4），所以路径S-3-2-D被确定为新的Pareto最优路径；R6也到达节点1，成为节点1的第二个PNDR，并在节点1触发R7。

在时刻6，R7到达D点，但由于R7被D处已有的PNDRs占优，所以R7没有找到任何新的Pareto最优路径，R7涟漪消失。此时已没有活跃涟漪，所以涟漪接力赛结束。

这时，根据终点D的所有PNDRs（即R2、R4和R6）所对应的路径，就可确定出完整的Pareto前沿。

2.2.2 一对多的MOPOP的RSA设计

在针对一对一MOPOP的RSA基础上，只需修改RSA中的微观智体行为（即不存在终点，每个PNDR总是会在节点触发一个新的涟漪）就可以将其扩展用于求解一对多的MOPOP。在一对多的MOPOP中，对于给定起始点S，需要为路网中其他(NN-1)个节点中的每个节点均找到完整的Pareto前沿。如图3所示，本小节给出了针对一对多MOPOP的RSA的步骤细节。

步骤1、步骤2与针对一对一MOPOP的RSA的步骤1、步骤2相同。

步骤3如果r=1,2,…,NR，都有SR(r)=0，即不会产生新的涟漪，则转到步骤7；否则，转到步骤4。

步骤4与针对一对一MOPOP的RSA的步骤4相同。

步骤5对于任意节点n，如果至少存在一个1≤r≤NR，使得SR(r)=1，且A(E(r),n)=1，R(r)≥Ch(E(r),n)，即涟漪r是一个到达节点n的涟漪，那么，将节点n上所有的到达涟漪（如果到达涟漪1的数目超过1个）进行比较，并把到达涟漪也与节点n上当前的PNDRs进行比较，找出其中的PNDR。节点n的每个到达涟漪（即涟漪r）将在节点n触发一个新的PNDR：令NR=NR+1；设E(NR)=n，T(NR)=r，R(NR)=R(r)-Ch(E(r),n)；设SR(NR)=1；ΩPNDR(n)=ΩPNDR(n)+{NR}；涟漪r从起始点S到达节点n的路径成本记录为Fi(NR,n)(i=1,2,…,NObj)。

图3 RSA确定一对多MOPOP的完整Pareto前沿的示例Fig.3 Illustration about how complete Pareto front is identified for one-to-all MOPOP by RSA

步骤6与针对一对一MOPOP的RSA的步骤6相同。

步骤7如果涟漪r∈ΩPNDR(n)，1≤r≤NR，则[F1(r,n),F2(r,n),…,FnObj(r,n)]表示节点n的一个Pareto点，涟漪r从起始点S到节点n的旅行路径为一个Pareto最优解。这样，每一个非起点的节点n上的所有PNDRs确定了该节点的完整的Pareto前沿和所有的Pareto最优路径。

通过修改RSA，还可以扩展到其他一些更复杂的MOPOPs。许多传统的路径优化方法（如Dijkstra算法和A*算法）都是集中式的、全局信息和基于逻辑规则的算法，对全局信息的需求往往意味着针对具体问题的定制化修改是困难的，而RSA是一个分散的、基于多智体的仿真模型。每个节点只需要通过其到达涟漪的信息来决定其自身产生和传播新涟漪的行为。RSA通过简单地修改节点的行为，可以很容易地应用于各种路径问题（包括一些传统方法可能难以解决的问题）。例如，当涉及到具有时间窗口或随时间动态变化的路网时，Dijkstra算法和A*算法甚至在单目标优化问题上也会遇到困难，通常需要进行繁琐的修改。而RSA只要简单地引入节点的涟漪等待和联合触发行为，就可以处理与时间窗口和时变路网相关的路径优化问题[29-31]。同理，通过对本文的RSA进行简单修改就可以应用求解于时间窗口和时变路网相关的MOPOPs。

3 理论分析

对于求解MOPOP的RSA的最优性和复杂性，有如下理论保证。

引理1假设涟漪到达一个节点，如果这个涟漪不是该节点的PNDR，那么任何从S到D包含这个涟漪的路径都不是Pareto最优路径。

证明假设p1为到达节点n的某个涟漪所经过的包含NL1个节点的路径，p2为节点n处一个PNDR涟漪所经过的包含NL2个节点的路径，可得出p1(1)=p2(1)=S，p1(NL1)=p2(NL2)。根据Pareto最优定义，如果经过p1的涟漪不是节点n的PNDR，则可得出fk(p1)≥fk(p2)(k=1,2,…,NObj)，fh(p1)＞fh(p2)(h∈[1,2,…,NObj])。

任何包含p1并连接S和D的路径可以表示为p4=p1+p3。然后，构建一条新的路径p5=p2+p3，显然它也连接S和D。根据目标函数的计算公式（2）以及Ck(i,j)的非负性，可得到fk(p4)=fk(p1+p3)≥fk(p2+p3)=fk(p5)(k=1,2,…,NObj)和fh(p4)=fh(p1+p3)＞fh(p2+p3)=fh(p5)。这意味着p5＞p4。所以，任何包含p1的路径都不是连接S和D的Pareto最优路径。

引理2假设一条路径p*是连接S和D的Pareto最优路径，那么当涟漪接力赛结束时，必然在D处存在一个被触发的涟漪，并且该涟漪的旅行路径就是这条路径p*。

证明假设引理2为假，即p*中必有一个节点p*(i)（1＜i≤NL*，NL*表示p*中的节点数），经过旅行路径p*(1),p*(2),…,p*(i-1)到达节点p*(i)的涟漪不是该节点的PNDR。那么，根据引理1，由于p*包含了路径[p*(1),p*(2),…,p*(i-1)]，所以不是Pareto最优的。因此，引理2必为真。

引理1说明PNDRs在中间节点上排除了从S到D的Pareto最优路径上所有的无关涟漪，这大大提高了计算效率，且所有在节点D上触发的涟漪都对应着Pareto最优路径，这是最优性的必要条件。引理2保证当涟漪接力赛结束时，连接S和D的每条Pareto最优路径都在D处触发了相应的涟漪，这是最优性的充分条件。因此，在引理1和引理2的基础上，可得到关于本文所提出的RSA的最优性的如下定理。

定理1在针对MOPOP的RSA中，当涟漪接力赛结束时，完整的Pareto前沿是由在D点触发的所有涟漪决定的。

这里讨论的针对一对多MOPOP的RSA的复杂性，可看作是针对一对一MOPOP的RSA的复杂性的上界。

定理2在一个具有NN个节点、NL条路径和给定起始点S的路网中，假定(NN-1)个节点中的每个节点的完整Pareto前沿平均具有NPP个Pareto点，那么对于具有NObj个目标函数的一对多MOPOP，相应的RSA的计算复杂度约为O(NObj×NL×NPP2)。

证明根据定理1，可知在涟漪接力赛中平均每个节点（S以外的节点）都有NPP个PNDRs并触发NPP个涟漪。RSA主要分为三个基本的计算步骤：（1）通过恒定的涟漪扩散速度增加涟漪的半径；（2）判断涟漪是否到达相邻节点；（3）判断到达涟漪是否被节点上已有的PNDR所占优。假设每个节点平均有2×NL/NN链接，涟漪经过一条路径平均需要NATU个时间单位。那么，在该涟漪消失之前平均需要(2×NATU+NObj+NObj×NPP)×2×NL/NN次计算。由于起始点S只会产生一个涟漪，而其他(NN-1)个节点平均会产生NPP个涟漪，因此，当所有的涟漪都消失时，即涟漪接力赛结束），需要进行(1+(NN-1)×NPP)×(2×NATU+NObj+NObj×NPP)×2×NL/NN次计算。通常情况下，NPP＞＞NObj并且NObj×NPP≫2×NATU，所以，RSA的计算复杂度大约为O(NObj×NL×NPP2)。

文献[21]中的方法求解一对多MOPOP时，对每一个非起点的节点都要进行一次一对一MOPOP求解，总共需要运行(NN-1)次。每次求解一对一MOPOP平均需要运行大约NObj×k2/2次某种求解前k条单目标最短路径的算法；假定用文献[29]中的求解前k条单目标最短路径的算法求解，则单次运行的复杂度为O(NATU×NL×k)。通常k具有与NPP相似的数量级，因为NPP条Pareto最优路径是从NObj×k条单目标最短路径中通过比较筛选得出的。所以，文献[21]的方法求解一对多MOPOP的复杂度约为O(NN×NObj×NATU×NL×NPP3)。显然，相较文献[21]的方法而言，本文所提出的新的RSA的计算复杂度大大降低了，尤其是在NN和NPP都很大的大规模网络问题中。

表1 平均比较实验结果Table I Average comparative experimental results

4 算法测试分析

4.1 比较算法

本文第3章给出了针对MOPOP的RSA的最优性的理论证明，在这一章还将给出实验证明。为此，将新的RSA与文献[21]的方法、NSGA-II[16]和AOF[4]进行对比。其中AOF方法采用不同的权重组合将NObj个优化目标整合成一个单一目标函数，然后应用Dijkstra算法求解单目标最短路径，不同权重组合下，Dijkstra算法一般会输出不同的路径，AOF基于这些不同的路径生成Pareto前沿。

4.2 测试方案与性能指标

本实验中采用了文献[21]的设置，在测试中使用节点总数NN=[25,36,49]、节点平均链接数NAL=[4,6]和优化目标数NObj=[2,3]来调整实验的规模，对每一组[NN,NAL,NObj]值，随机生成100个路网。实验结果如表1和图4所示。在图4中，上边的子图是实验中的一个路网(NN=49,NAL=4,NObj=2)，以及用于示例的两条Pareto最优路径（对于目标函数f1，红色单点划线标识的为最佳路径；而对于目标函数f2，红色双点划线则为最佳路径）；下边的子图给出了四种不同方法计算出的Pareto前沿。

图4 当NN=49时，用不同方法求解所得Pareto前沿Fig.4 Example of solutions by different methods(NN=49)

4.3 测试结果与分析

从表1、图4可以看出：

（1）在所有实验中，本文提出的新的RSA和文献[21]中的方法具有完全相同的NPPF（找到Pareto点的个数）和RFCPF值（找到完整Pareto前沿的比率，即在路网中某种方法找到的完整Pareto前沿的次数与节点数的比值）。由于文献[21]中的方法在为MOPOP寻找完整的Pareto前沿时具有理论最优性保障，所以表1和图4可以作为新的RSA最优性的实验证明。

（2）在平均计算时间（秒）（Computational Time，CT）方面，新的RSA算法与AOF方法有相似的CTs，而AOF方法在大多数测试中计算效率是高于NSGA-II和文献[21]中的方法的。

（3）表1和图4清晰地表明，NSGA-II或AOF方法往往无法找到完整的Pareto前沿。在RFCPF方面，AOF方法由于不能找到位于Pareto前沿非凸部分的Pareto点，所以表现是最糟糕的。虽然有时AOF方法找到的Pareto点的个数多于NSGA-II，但由于绝大多数Pareto前沿都是非凸的（即使构成前沿的Pareto点很少），所以NSGAII找到完整Pareto前沿的可能性反而高于AOF方法。

（4）如图4所示，NSGA-II通常很难找到真正的Pareto点，即NSGA-II得到的相当一部分解通常不是Pareto最优的。由于NSGA-II本质上是随机搜索算法，对于单目标优化问题也无法保证理论上的最优性，因此在求解多目标优化问题上效果更加糟糕。

（5）就NPPF和RFCPF而言，问题规模(NN,NAL,NObj)对新的RSA和文献[21]中的方法没有影响，因为这两种方法都有理论保证找到完整的Pareto前沿。但随着问题规模变大，AOF和NSGA-II的求解效果会变差。

（6）就CT而言，问题规模对所有4种方法都有显著影响，都会引起CT增加。不过新的RSA与AOF方法的CTs随问题规模变化较慢，而文献[21]方法和NSGA-II的CTs随问题规模增加很快。

4.4 一个复杂的一对多MOPOP算例

4.1 节中实验的问题规模很小，即所有的实验都只是一对一的双目标路径优化问题，最大的路网只有NN=49个节点，最复杂的Pareto前沿只有30多个Pareto点。本节求解了一个NN=400的三目标一对多MOOP，其中节点1为起始点。在NN=400的一对多MOPOP问题中，总共需求解399个Pareto前沿。本文提出的新的RSA只需在路网上进行一次涟漪接力赛，就可以找到全部399个完整的Pareto前沿，而无需像NSGA-II、AOF和文献[27]中的方法，必须运行399次，才能解决这个一对多MOPOP问题。新的RSA的计算结果显示，在这399个完整Pareto前沿中，最复杂的一个Pareto前沿具有2 463个Pareto点（当节点360是终点时）。

本实验中只比较了NSGA-II和AOF方法，而没有采用文献[21]中的方法，因为文献[21]中的方法在求解这个一对多MOPOP问题时，会因为问题规模太大而耗尽计算机内存，从而导致宕机。

图5的顶部子图给出了在路网中选择不同节点作为终点（节点1始终为起始点）时，不同方法找到的Pareto点的个数。可以看出，当一个完整Pareto前沿具有很多Pareto点时，NSGA-II和AOF方法通常只找到很小比例的真正Pareto点。图5左下的子图比较了在节点360为终点时（即最复杂的情况下），AOF方法与RSA所找出的Pareto点的差异，右下的子图比较了RSA和NSGA-II在相同的条件下找出的Pareto点的差异。实际上，在节点360为终点的情况下，NSGA-II没有找到任何真正的Pareto点。

在计算效率方面，本文所提出的RSA运行一次找到399个Pareto前沿只需大约500 s。文献[21]中的方法在运行数天后只会宕机。NSGA-II通常耗费数小时，但最终会产生许多假的Pareto点。AOF方法耗时约400 s，但如图5所示，它只找到了很小比例的真正的Pareto点。

5 结束语

现有的RSA只针对SOOP，如文献[21-23]求解MOOP所使用的RSA只能求解前k个单目标最优解。本文首次提出了一种真正针对MOPOP的RSA算法，仅通过一次涟漪接力赛就可以计算出完整的Pareto前沿。新的RSA是基于多智体的自下向上的仿真模型，通过提出PNDR的概念并由之定义微观智体的涟漪激发和扩散行为，在涟漪接力赛的宏观层面上就可以表现出完整的Pareto前沿。新的RSA具有求解出完整Pareto前沿的理论保障，因此可作为研究MOOP的基准方法来衡量其他离散MOOP方法（如遗传算法和粒子群算法）性能。未来的工作可以放在分布式并行RSA的设计上，并将其应用于可转换为MOPOP的各种实际多目标优化问题的求解。例如在针对突发事件的应急资源配置的问题中对应急路径的规划，以应急路径的时效性（即行程时间）和可靠性（即行程时间可靠度）为双目标建立模型，对最优路径进行搜索。在多目标无人机路径规划问题中，以路径长度和路径受威胁程度为优化目标，建立无人机路径规划的双目标优化模型，求解从起始点到目的地路径的Pareto前沿。然后就本文中的RSA在找到Pareto点的个数、找到完整Pareto前沿的比率和平均计算时间三个方面的测试结果与其他算法的性能进行比较，以验证新方法的有效性和高效性。

图5 当NN=400时的一对多MOPOPFig.5 Example of one-to-all MOPOP(NN=400)