线性宽象限相依*下折现累积理赔尾概率的一致渐近估计

钱 欢，彭 千

（1.安徽大学数学科学学院，安徽合肥230601；2.安徽农业大学理学院，安徽合肥230036）

在保险和金融领域，对折现累积理赔过程的研究具有重要意义，其尾概率估计可直接用于计算公司的破产概率。假定理赔额{Xi,i≥1}和理赔时间间隔{θi,i≥1}均为独立同分布的随机变量序列，在不同条件下，文献[1-2]得到了折现累积理赔或保险公司破产概率的一致渐近估计。随后，假定{Xi,i≥1}满足某种相依结构，或{Xi,i≥1}与{θi,i≥1}之间满足某种相依结构，文献[3-4]研究了公司有限时间破产概率的一致渐近估计。本文旨在研究{Xi,i≥1}满足线性宽象限相依*（LWQD*）时，公司折现累积理赔尾概率的一致渐近估计。

1 预备知识

考虑一个更新风险模型，理赔额{Xi,i≥1}与理赔时间间隔{θi,i≥1}均为随机变量序列。定义理赔到达时间,n≥1，约定几乎处处有0=τ0＜τ1＜τ2＜…，则到t时刻为止，理赔次数的更新计数，t≥0。当0＜t＜∞时，过程为Nt=sup{n≥1,τn≤t},t≥0，其均值函数为E(Nt)＜∞；当t=0时，E(N0)=0。通过上述均值函数来定义Λ={t＞0,E(Nt)＞0}={t＞0,P(τ1≤t)＞0}。令常数利息率r≥0，则到t时刻为止的折现累积理赔过程为

约定当Nt=0时，上述求和的值恒为0。

定义1[5]设{Xn,n≥1}为一列随机变量，若存在一列正常数序列{gn,n≥1}，使得对所有的n≥2，x,y∈(-∞,∞)，以及任意正常数序列{an,n≥1}，有

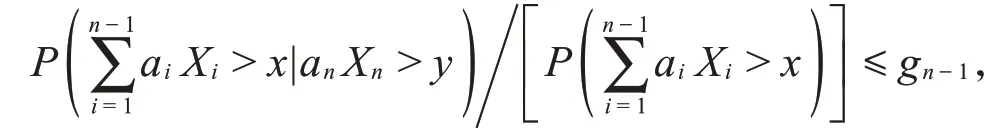
则称{Xn,n≥1}满足线性宽象限相依*，其中{gn,n≥1}称为控制系数。

不妨设对任意的n≥1，有gn≥1；若不然，则存在一列大于1的常数序列使上式仍然成立[5]。假定理赔额{Xi,i≥1}为一列LWQD*非负同分布随机变量，且理赔额的分布属于强次指数族，通过构造LWQD*随机变量加权和Kesten型不等式，证明折现累积理赔尾概率的一致渐近估计式，扩展了文献[6]的结果。

定义2[7]设X是一个随机变量，x是任意实数，函数F(x)=P(X≤x),-∞＜x＜∞称为X的分布函数，记其尾分布为Fˉ(x)=1-F(x)。对于任意的分布函数，本文所有的极限关系均指x→∞。对于两个正值函数f(·)和g(·)，有

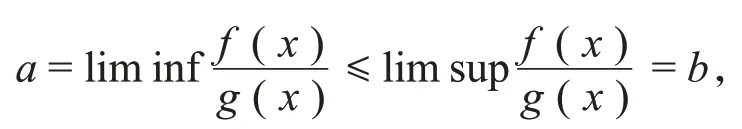
当a=b=1时，记作f(x)～g(x)；当b=0时，记 作f(x)=o(g(x))；当0＜a≤b＜∞时，记 作；当b≤1时，记作f(x)≲g(x)；当a≥1时，记作f(x)≳g(x)。对于两个实数m和n，记m∨n=max{m,n}。另外，IA表示事件A的示性函数。

定义3[8]如果非负随机变量X具有有限均值，且满足，则称非负随机变量X（或其分布函数F）属于强次指数族（S*族），记作X∈S*（或F∈S*）。

定义4[8]如果对于y∈(-∞,∞)，有，则称实值随机变量X（或其分布函数F）属于长尾族（ℒ族），记作X∈ℒ（或F∈ℒ）。

注1由文献[8]可知，长尾分布族具有如下基本性质：

若F∈ℒ，则ℋ(F)={h取值于[0,∞):h(x)↑∞,↓0,且。易证，对于任意的h(x)∈ℋ(F)和任意固定的K＞0，有。

引理1[9]若F∈ℒ，a、b为任意固定常数且0＜a≤b＜∞，则对任意的h(x)∈ℋ(F)，对c∈[a,b]一致地有。

引理2[6]若F∈S*，a、b为任意固定常数，且0＜a≤b＜∞，则对任意的h(x)∈ℋ(F)，ε＞0，以及充分大的x，对c∈[a,b]一致地有

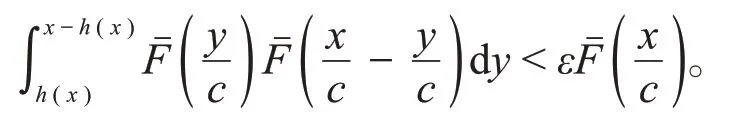
引理3[6]如果{Xi,i≥1}为一列LWQD*非负随机变量，共同分布F∈S*，a、b为任意固定常数且0＜a≤b＜∞，则对n≥1，i≥1以及充分大的x，对ci∈[a,b]一致地有

引理4若{Xi,i≥1}为一列LWQD*非负随机变量，共同分布F∈S*，控制系数为{gi,i≥1}，令a、b为任意固定常数，且0＜a≤b＜∞，则对任意的ε＞0，存在一个仅依赖于ε、F、a、b，而与n无关的非负常数K，使得对所有的x≥0和n≥1，对(c1,c2,c3,…,cn)∈[a,b]n一致地有

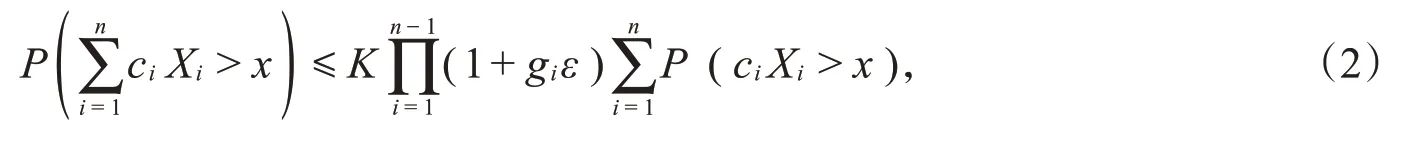
证明为了方便，定义。当x为整数时，利用数学归纳法可证明式（2）。当n=1时，式（2）显然成立。假设式（2）对n成立，下面证明对n+1也成立。记

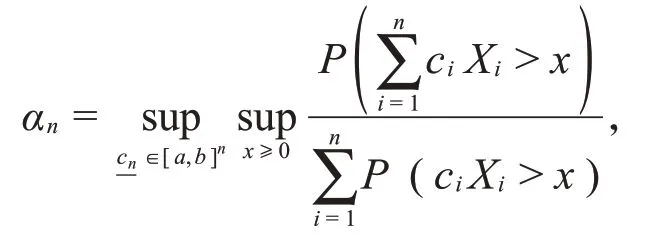
由于F∈S*⊆ℒ，由注1可知，存在h(x)∈ℋ(F)，于是

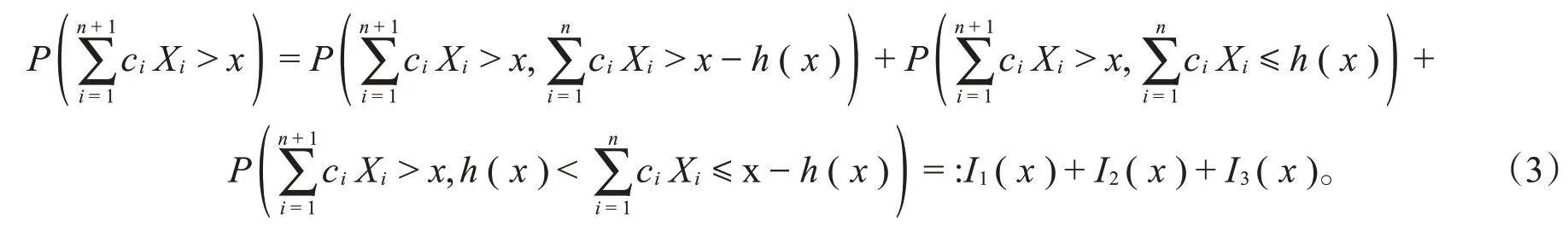
由引理1可知，存在充分大的A＞0，使得当x＞A时，对-cn∈[a,b]n一致地有

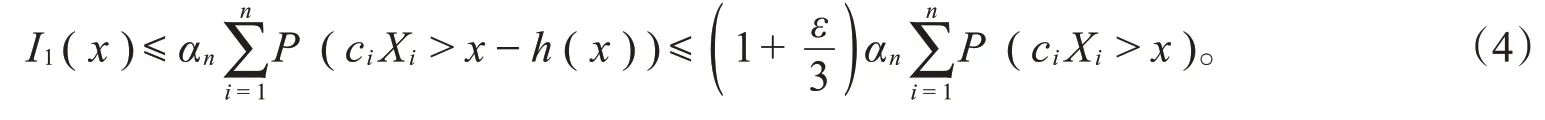
同理，

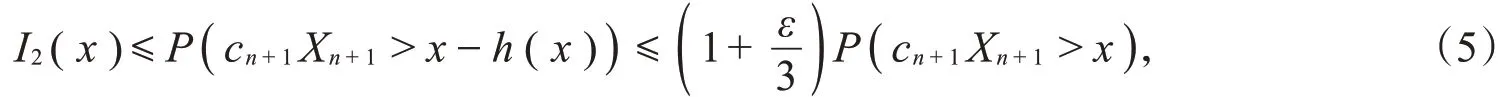
由于[h(x)]≤h(x)，故，因此只需考虑h(x)取整数值情形即可。由LWQD*和αn的定义可知

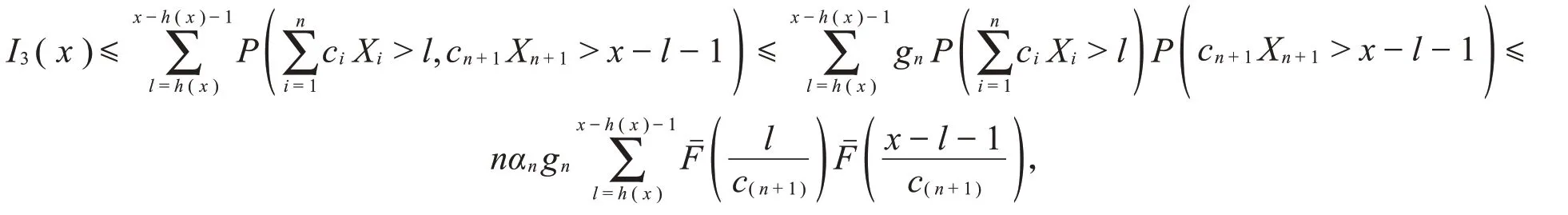
故由F∈S*⊆ℒ以及引理2可知，对上述充分大的A＞0，当x＞A时，对一致地有

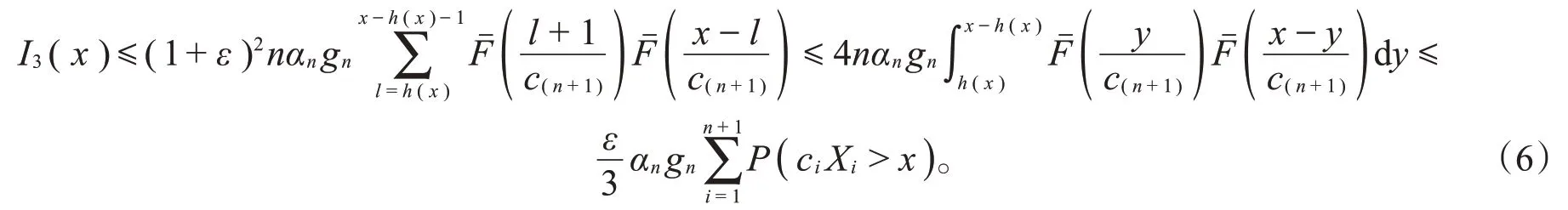
将式（4）～（6）代入式（3），得当x＞A时，对一致地有

另一方面，当0≤x≤A时，对一致地有

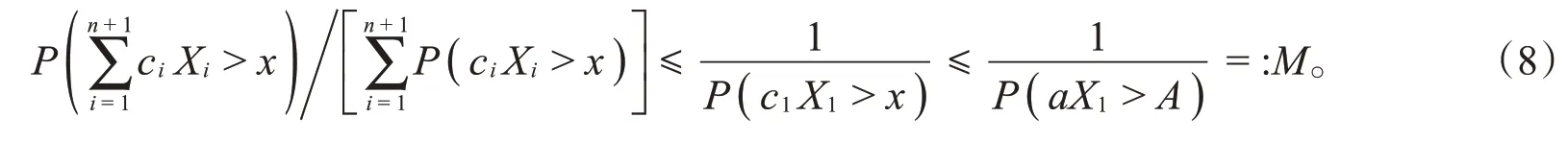
由归纳假设，存在一仅依赖于ε、F、a、b，而与n无关的非负常数，使。结合式（7）和（8）有

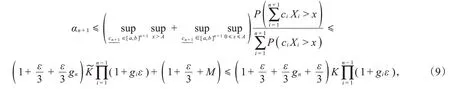
其中，K=∨(3/ε)(1+ε/3+M)。由式（9）和gn≥1得，故式（2）对n+1成立。

当x为非负整数时，记[x]为x取整数。由非增，x-1≤[x]≤x以及F∈S*⊆ℒ可知，

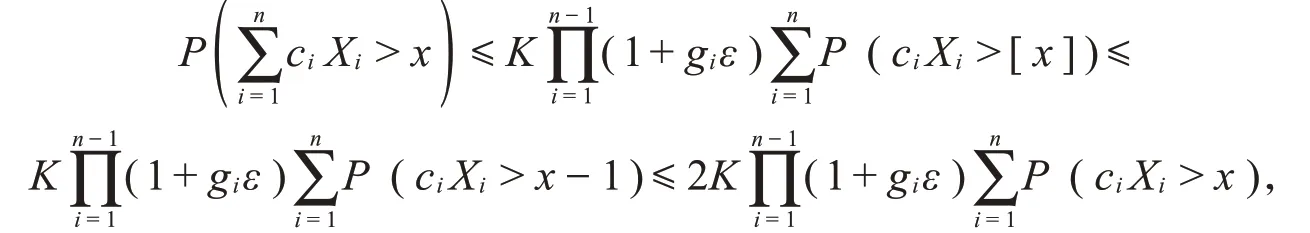
最后一步只对x充分大时成立。若x非充分大，则类似于式（8）中方法可证明结论成立。

2 主要定理及其证明

定理对于上述非标准更新风险模型，考虑折现累积理赔过程（1），若F∈S*，且存在ε＞0，有

则对任意的t∈Λ一致地有

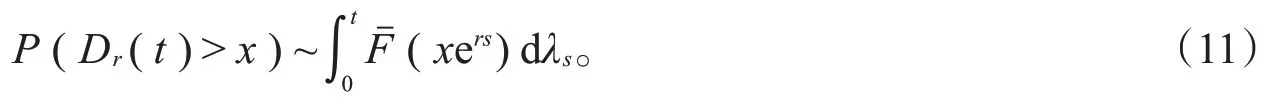
证明为了方便，定义，对任意正整数N，有

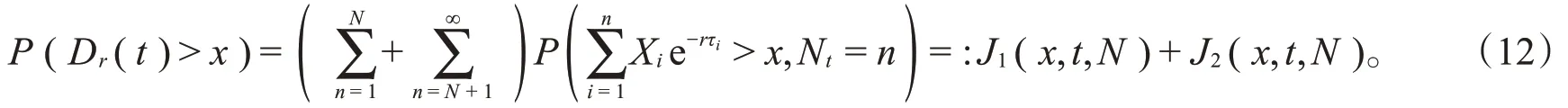
对于J1(x,t,N)，以τ1,τ2,τ3,…,τn+1作为条件事件，由X1,X2,X3,…,Xn+1与τ1,τ2,τ3,…,τn+1相互独立以及引理3可知，

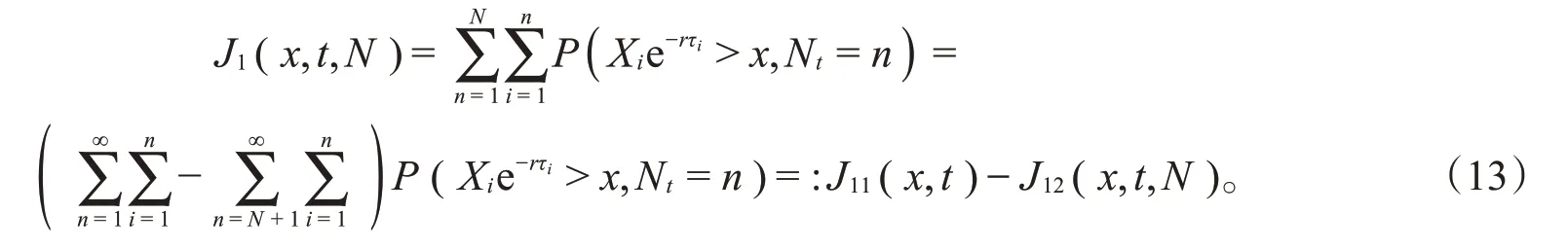
对J11(x,t)交换求和顺序，并由知，对任意的t∈Λ一致地有

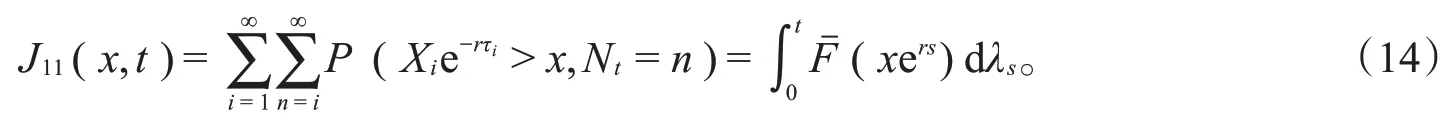
由于几乎处处有0＜τ1＜τ2＜…，所以对任意的t∈Λ一致地有

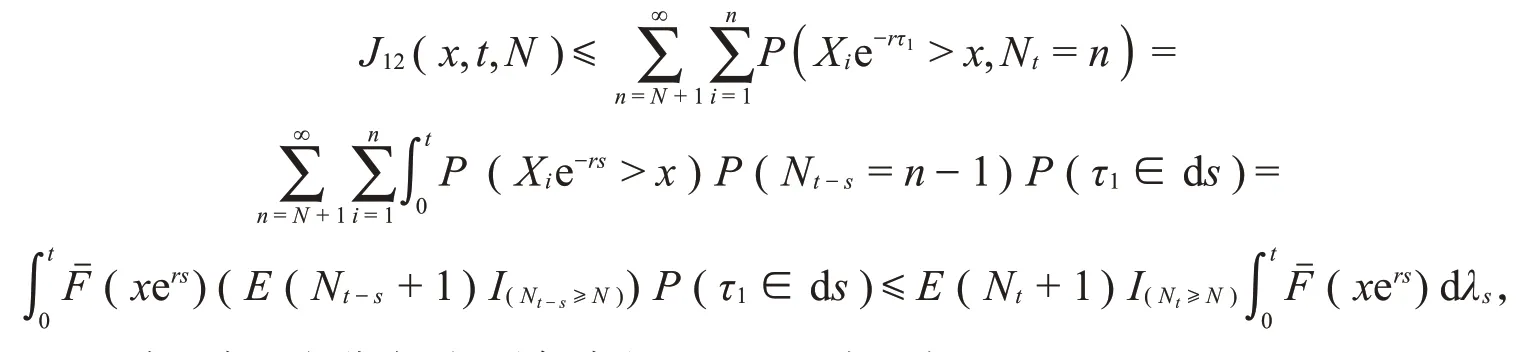
故由E(Nt)＜∞可知，当N充分大时，对任意的t∈Λ一致地有

将式（14）（15）代入式（13），由δ的任意性，即得对任意的t∈Λ一致地有

对于J2(x,t,N)，以τ1,τ2,τ3,…,τn+1作为条件事件，由X1,X2,X3,…,Xn+1与τ1,τ2,τ3,…,τn+1相互独立以及引理4知，对任意的t∈Λ一致地有

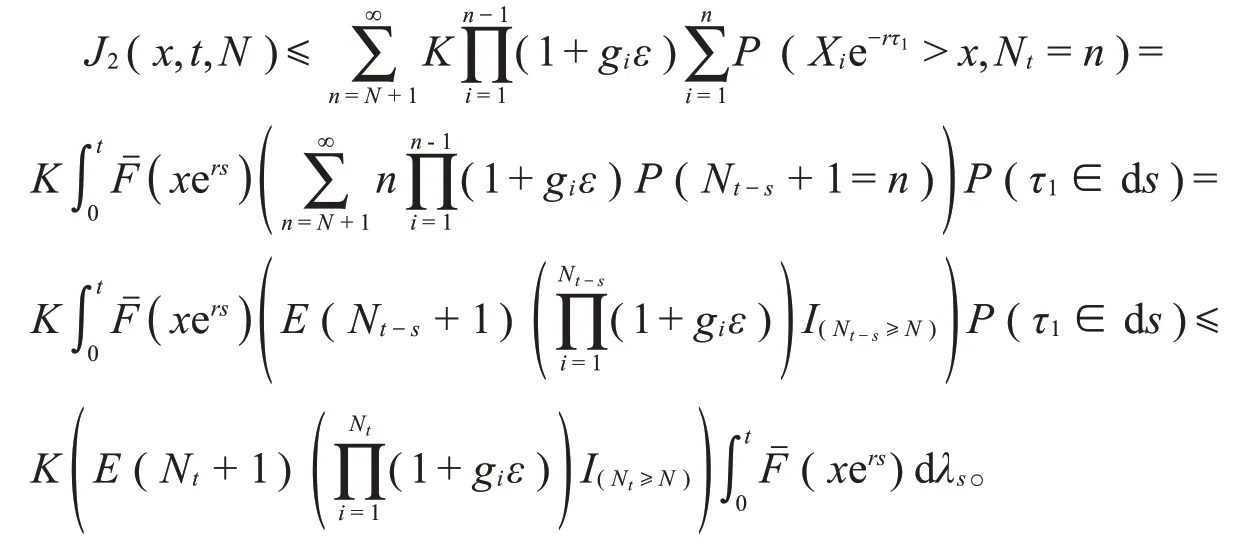
将式（16）（17）代入式（12），由δ的任意性，即得式（11）。

注2若对于控制系数{gi,i≥1}存在充分大的常数C，使得||gi≤C,i≥1，则条件（10）自然成立[10]。

3 结论

本文主要研究了保险公司的理赔额在满足线性宽象限相依*的情况下，折现累积理赔尾概率的一致渐近估计。研究改善了理赔额独立同分布这种过于理想化的情况，并且这类相依结构是比较宽泛的，在该相依结构下，构造了随机加权和Kesten型不等式解决了相关问题，为类似课题的研究提供了思路。不足之处是没有考虑理赔额和理赔时间间隔之间存在相依结构，理赔额服从的分布没有推广到更大的分布族，今后需继续深入研究。