一种面向嵌入式平台的脑电信号注意力检测方法

刘文政，纪博伦，赵 靖,*，张 伟，吴正平

(1.燕山大学 电气工程学院，河北 秦皇岛 066004；2.三江学院 创新创业学院，江苏 南京 210012)

0 引言

注意力是指人内心对某种事物集中能力的描述，它包含信息的获取、解码和调整控制等一系列复杂的处理过程，是人类进行学习活动的前提。通过对脑电信号的获取和解码实现对注意力水平的检测，这一技术在教育和医疗康复等领域都有着广泛的应用[1]。在教育领域，检测多动症患儿的注意力指数来进行神经反馈训练，可以有效改善患儿的注意力水平；在医疗康复领域，检测患者的注意力水平帮助运动障碍患者恢复一定的自主行为能力，提高生活品质。

脑机接口(brain-computer interface,BCI)作为一种不依赖于人的外周神经和肌肉直接通过脑电活动来传递思维信息的人-机交互技术，可以解析出被试者大脑活动信号中携带的注意力信息[2]。由于脑电(electroencephalogram,EEG)信号具有非侵入、成本低、方便易用、时间分辨率高的优点，因此常被用于注意力检测的脑机接口研究[3]。在当前研究中，对注意力的检测通常是通过采集前额叶的EEG信号，提取其中的alpha频段(8～13 Hz)和beta频段(13～30 Hz)的能量作为特征进行分类[4]。NeuroSky公司开发了一款高集成度的脑电传感模块(TinkGear ASIC Module,TGAM)模块，其中集成了一种注意力计量算法(Attention Meter Method,AMM)，可以输出被试者的“eSense专注度”指数来表征被试者的注意力强度[5]。该模块基于嵌入式平台进行设计和实现，具有体积小、功耗低、佩戴方便的优点，在娱乐和教育领域的注意力检测产品中得到了广泛应用[6-8]。但是受到AMM算法检测精度较低的影响，此类系统容易频繁输出错误结果而使被试者产生受挫感，从而降低被试者使用产品的积极性。

为提高注意力的检测精度，Liu等人[9]提出一种α+β+δ+θ+R算法，通过提取脑电信号中多个频段的能量特征并进行融合分类，提高了对注意力水平的分类精度。本课题组在前期研究中[10]提出了一种优化复杂网络算法(Optimized Complex Network Method,OCNM)，通过对单通道脑电数据进行相空间重构，并采用C-C算法[11]和Cao算法[12]优化重构节点间的网络参数，得到表征注意力水平的复杂网络模型后，提取该网络的平均度和平均聚类系数进行分类。交叉验证的结果表明，该算法的分类精度显著高于AMM算法和α+β+δ+θ+R算法。

OCNM算法虽然能够取得更高的检测精度，但是由于对存储容量和计算资源的需求量大，无法用在资源有限的嵌入式平台上，这极大地限制了该算法在娱乐和教育类产品中的应用潜力[13]。为此，本文针对嵌入式平台资源有限和OCNM算法计算量大之间的矛盾，从对OCNM算法的范式简化和参数优选出发，提出了一种面向嵌入式平台的改进OCNM算法，通过上位机的离线试验和STM32平台的在线试验，验证了该算法用于嵌入式平台注意力检测的有效性。

1 基于OCNM的注意力检测方法

1.1 OCNM算法

OCNM算法是在复杂网络分析的基础上，通过相空间重构将单通道脑电信号转换成复杂网络结构，进而提取专注和放松状态下的网络特征度量，实现对注意力水平的检测。其中，相空间重构部分采用延迟坐标嵌入法将一维时间序列通过延迟得到多维时间序列[14]。对一维脑电数据x进行相空间重构，得到如下形式的相空间矢量矩阵

(1)

式中,m为嵌入维数，τ为延迟时间，M为相空间重构后矢量点的个数。N为有效数据的长度，定义N=M+(m-1)τ。将每个相空间矢量Xi(i=1,2,…,M)视为网络中的节点，计算任意两个相空间矢量之间的欧式距离dij，并根据如下规则构造复杂网络的邻接矩阵

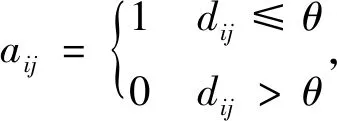
(2)

其中，θ为确定两点之间连接关系的阈值参数。对于构建好的复杂网络，提取平均度K和平均聚类系数C作为网络的特征，通过线性判别分析(Linear Discriminant Analysis,LDA)分类器进行分类。

在OCNM算法中，复杂网络是基于延迟时间τ、嵌入维数m和阈值θ三个参数进行构建的，因此这些参数的选取对网络结构和注意力检测的精度影响很大。本文分别采用C-C算法和Cao算法来优化τ和m，搜索满足网络连通性的最小阈值作为θ。

1.2 基于C-C算法的延迟时间优化

延迟时间τ的优化能够有消除相空间重构后维与维之间的相关性。本文使用目前确定延迟时间的常用方法C-C算法来确定最佳延迟时间。C-C算法通过嵌入时间序列的关联积分函数来确定最佳延迟时间，反映了时间序列相关性的变化规律。嵌入时间序列的关联积分函数为

C(m,N,r,t)=

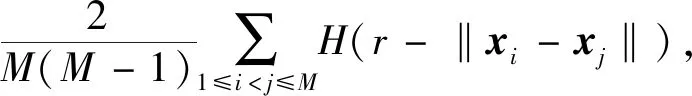
(3)

式中，M为相空间重构后矢量点的个数，H为阶跃函数，r>0为参考半径，xi为相空间重构后的矢量。将xi分解成τ个互不相关的时间序列：

S(m,N,r,t)=

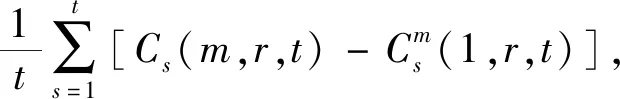
(4)

定义S(m,r,t)关于r的变化量：

ΔS(m,t)=max{S(m,rj,t)}-

min{S(m,rj,t)},

(5)

最优延迟时间τ就是S(m,r,N,t)的过零点和ΔS(m,t)的最小值。

1.3 基于Cao法的最小嵌入维数优化

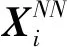
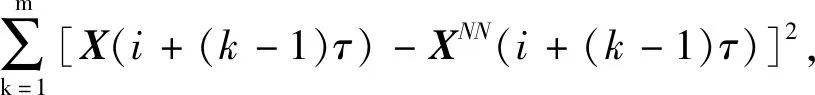
(6)

当m→m+1时，

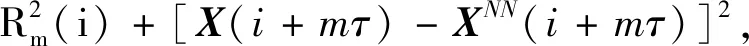
(7)

式中,定义相空间中的点由于维数增加1而引起的两个最近邻向量点间的距离的变化值

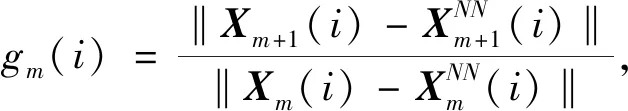
(8)

定义gm(i)的均值为

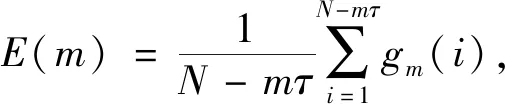
(9)

当嵌入维数从m变化到m+1时，E(m)的变化量为E(m+1)/E(m)。对于有限维系统，E(m)将随着维数的增加达到饱和，即变化量逐渐趋向于1。当E(m)的变化稳定后，便可以确定一个使相轨迹充分展开的最小的嵌入维数。

1.4 训练范式

为对OCNM算法进行参数优化和分类器训练，需要采集专注和放松两种状态下的多组脑电数据，用于估计复杂网络参数和训练分类器模型，然后提供给在线试验使用,其训练范式流程如图1所示。为此，在OCNM方法中采用了如下的训练范式。整个试验过程在安静的试验室中进行并由两部分组成，被试者按要求进行专注和放松两种认知任务：

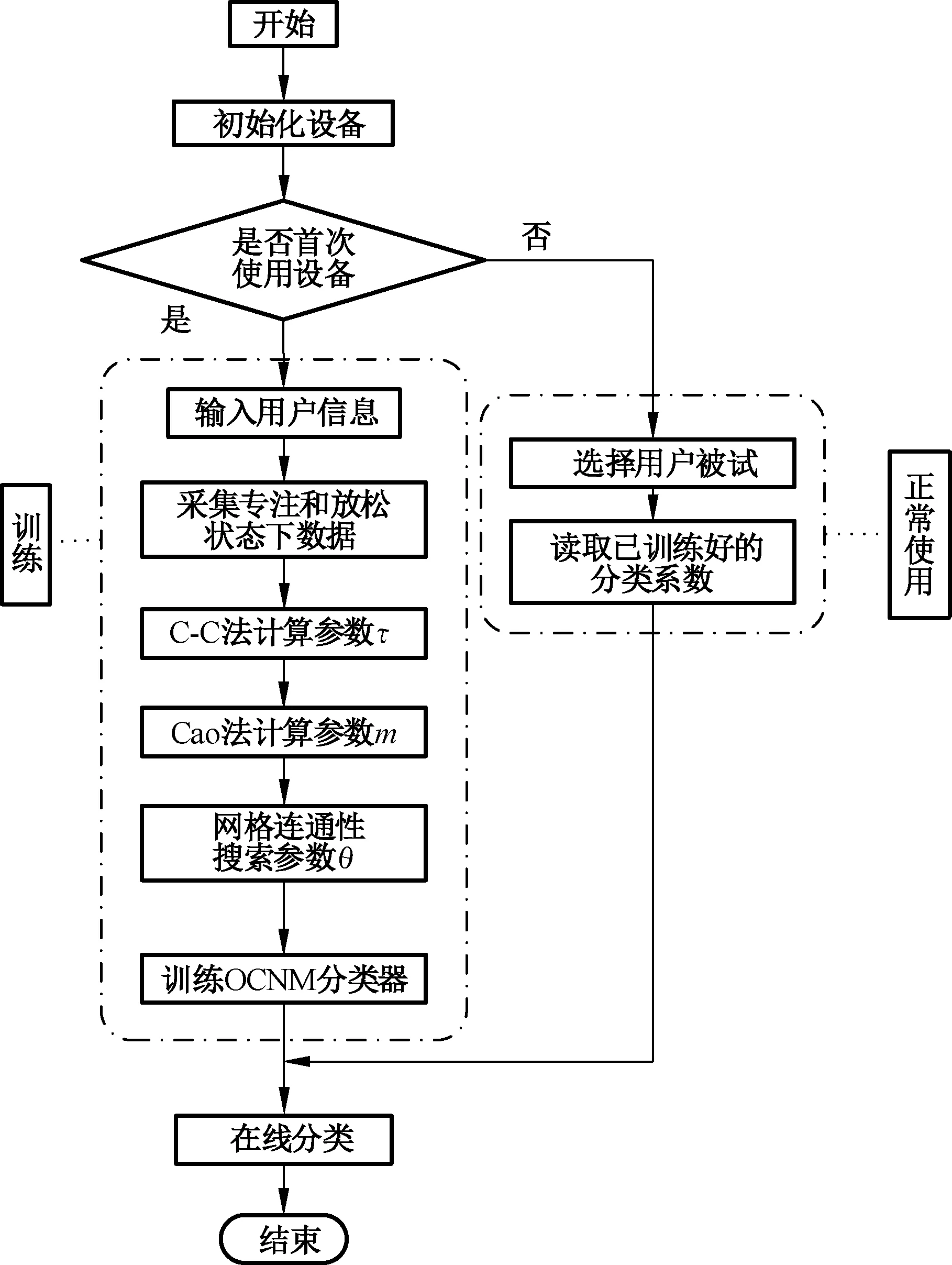
图1 OCNM法训练范式流程图Fig.1 Flowchart of training paradigm for ONCM method

1)放松任务：被试者背靠在椅子上观看蓝天白云图像，从而进入放松状态。

2)专注任务：被试者背靠在椅子上，按要求进行2位数乘法的心算任务，从而进入专注状态。

被试者需要进行40组试验，每组试验包括7 s的放松任务和小于15 s的专注任务，两种任务交替进行，共采集40组专注状态和40组放松状态的脑电数据用于参数训练[15]。

2 面向嵌入式平台的改进OCNM算法

2.1 范式简化

在注意力检测参数的训练过程中，为提取和统计专注和放松两种状态下脑电数据的差异性特征，因此需要多次重复试验的数据支持。为减小多次数据采集所需的试验时间和存储空间，本文对OCNM算法的试验范式进行了简化。

在OCNM算法的离线训练中，被试者需要进行总计40组试验，每组试验包括7 s的放松任务和小于15 s的专注任务，因此共需约880 s来采集专注和放松状态的训练数据，在512 Hz采样率下的训练数据大小为1 760 kB。由于在现有技术中，对于注意力检测参数的训练过程尚未有约定或最优的试验范式，往往是根据具体的认知任务和应用需求进行设计和调整。为了减少被试者训练所需的任务时间和训练数据量，本文针对专注和放松状态脑电信号的缓变特性，在训练范式上进行如下改进：被试者共开展2次30 s的专注试验和1次60 s的放松试验，将采集记录的连续数据分割为1 s长度的数据段，以得到120段脑电数据用于参数训练[16]。范式简化后的训练试验的时长总计为132 s，在512 Hz采样率下的训练数据大小为264 kB，在保证训练数据足够的前提下极大地缩短了试验时间以及减小了数据容量。进行范式简化后的训练数据采集流程如图2。

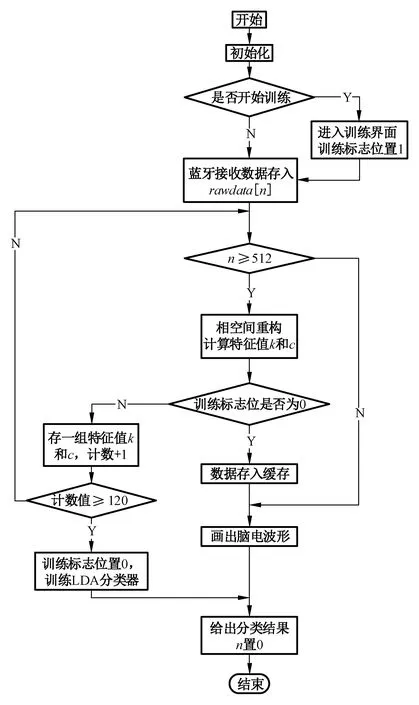
图2 OCNM法训练分类器流程图Fig.2 Flowchart of training classifier for ONCM method

首先记录试验者专注状态下脑电数据：试验者有4 s的休息时间，接着提示试验者准备开始专注试验，有2 s的准备时间，屏幕上出现三角提示箭头，2 s之后在箭头下方出现一道3位数的乘法运算题，试验者集中注意力计算题目，同时记录30 s专注状态下的试验数据(注：在记录15 s专注数据之后屏幕上的乘法题目会刷新，保证无论试验者计算速度快慢，试验者都处于专注状态，记录达到30 s数据之后系统会自动退出)，然后会有4 s的调整休息时间，此时不记录试验数据，之后再次开始重复上一专注试验过程；总共记录专注状态下2次30 s的脑电数据。

然后记录试验者放松状态下脑电数据：试验者有4 s的休息时间，接着提示试验者准备开始放松试验，有2 s的准备时间，试验者按指示注视空白屏幕并进入放松状态，同时记录60 s放松状态下的试验数据；总共记录放松状态下的1次60 s长度的脑电数据。至此采集训练数据部分结束。

2.2 参数优化

在OCNM算法中，需要对嵌入维数m、延迟时间τ、阈值θ三个参数进行优化和估计，所采用的C-C算法、Cao算法以及全连接搜索法的计算量大，运算过程复杂，尚无法在嵌入式平台上实现。为此，本文对上述参数对注意力检测精度的影响进行统计分析，通过网格搜索方法选取最优经验参数值来简化参数计算的过程。具体实施方法如下：

1)采用简化后的训练范式，对6名被试者分别采集专注和放松状态下的FPz通道脑电数据，预处理后建立离线数据集用于参数的优选。

2)在m=6∶1∶10、τ=5∶1∶10、θ=50∶25∶125范围内计算每种参数组合下的OCNM分类准确率。理论上参数选取的范围是不固定的，采用大范围随机选取参数组合进行准确率验证的方法效率极低，而且容易漏掉最优参数组合。在前期研究中发现，同一被试者的准确率随参数的不同而存在显著性差异，不同被试者的最优参数存在个体差异性，对多名被试者的统计表明最优经验参数值在这一范围内。

3)分别测试6名被试者在各个参数组合下的分类准确率。按照循环结构依次选取各个参数，在每个参数组合下进行相空间重构、计算特征值、进行LDA分类、10×10折交叉验证计算被试者的分类准确率数值，记为Xi(m,τ,θ)∈RNC*NS。其中，NC表示通道，NS表示采样点，i表示被试者编号。此时为了尽可能地平衡不同被试者之间的个体差异性，选择出一个符合大多数被试者的最优参数，利用下式计算这一组参数值的平均准确率

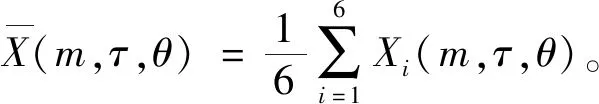
(10)

4)通过网格搜索选取平均准确率最大的参数组合，作为最优经验参数值以开展后续的试验验证。

3 试验验证

3.1 硬件系统

为验证本文所提出的改进OCNM算法，选用Sichiray公司基于TGAM模块开发的脑波头带设备采集脑电信号，通过hc-05蓝牙传输给搭载STM32F407单片机的嵌入式平台进行解码，将改进OCNM算法移植到该平台上进行验证。

1)嵌入式平台

嵌入式平台使用STM32F407系列单片机作为控制芯片。该芯片配备32位高性能的ARM Cortex-M4处理器内核，时钟高达168 MHz，具有1 024 K的FLASH、192 K的SRAM存储器容量，提供睡眠、待机和停止3个低功耗模式，在不需CPU运行时节省功耗。在10×10 mm的封装内，具有114个可耐5 V的IO口，拥有大量通信接口，支持SWD和JTAG调试。不仅支持浮点运算，还具有多种DSP指令集，可以直接使用函数库进行多种复杂运算，例如求模、滤波和矩阵处理。

该平台使用14寸TFT-LCD液晶屏幕来显示被试者的脑电波形，使用hc-05蓝牙来连接脑波头带与STM32F407单片机。提前使用USB转TTL串口把hc-05蓝牙配置成与脑波头带相匹配的模式，hc-05作为无线通信模块插入单片机IO口，自动搜索并连接Sichiray脑波头带实现数据传输。

2)Sichiray脑波头带

Sichiray脑波头带使用干电极测量技术，以512 Hz的采样率和较高的信噪比采集脑电信号，该设备在前额正面FPz位置布设了干电极脑电传感器，可以采集前额区域的原始脑电信号并通过蓝牙传输到嵌入式平台进行处理，同时设备中集成了注意力检测中常用的AMM算法，方便进行两种算法的对比验证。

3.2 验证流程

试验在无电磁屏蔽的安静实验室环境中进行的，共6名被试者参与了本试验。所有被试者都坐在舒适的扶手椅上，并通过液晶屏幕接受试验指导。试验过程分为离线、在线两个阶段[17]。

在离线试验阶段，采集6名被试者脑电数据并选取最优经验参数。根据屏幕提示，被试者分别进行相应的专注和放松任务，采集并存储两种状态下前额FPz通道的脑电数据，即作为专注和放松状态下两部分数据。分别针对各个参数的选取以及不同的参数组合，采用10×10折交叉验证计算系统的分类平均准确率，分析不同参数组合对系统分类性能的影响，并为改进OCNM算法选取在线参数。

在在线试验阶段，使用集成了改进OCNM算法的嵌入式平台，对6名被试者的在线分类结果进行测试。在线系统首先采集被试者的训练数据，并传输到嵌入式平台上进行分类器的训练；在测试阶段实时采集被试者的脑电信号，每隔1 s进行一次注意力分类，并将分类结果显示在液晶屏上。记专注状态为E1，放松状态为E2，在线准确率的统计方法为：试验过程中由实验人员给出随机口令，当随机口令为“专注”时，被试者进行相应的专注任务如计算三位数的心算乘法；当随机口令为“放松”时，被试者进入相应放松状态如观看空白图纸。在给出口令后的4 s内，若显示屏上的注意力分类结果与期望的状态变化一致，如E2→E1→E2或E1→E2→E1，则记本次分类结果正确，否则记本次分类结果错误；被试者 需进行30次试验并统计分类结果，计算在线分类的平均准确率。

4 试验结果分析

4.1 范式简化对系统分类性能的影响

考虑到训练数据量对分类性能的影响，本文首先对不同训练数据量下OCNM算法的分类性能进行了离线分析，在10×10折交叉验证中，对随机排序后的72组训练数据，分别选取前N组用于OCNM分类器的训练。当N取不同值时OCNM算法的分类准确率如图3所示。从图中可知，当N=15时，OCNM算法取得最低的平均准确率66.97%；随着训练数据量的增大，平均准确率也有所升高，当N=65时，取得最高的平均准确率72.71%；当N≥40时，训练数据量的增大已经不再显著提高平均准确率，反而会延长训练时间并增大数据存储负担。

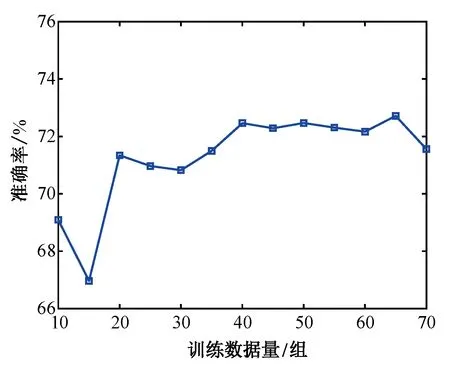
图3 不同训练数据量下的分类准确率曲线Fig.3 Classification accuracy with different amounts of training data

表1展示了不同训练数据量下简化范式所需的存储数据容量和训练时间。在传统范式中，每组训练试验包括7 s的放松任务和15 s的专注任务，两者之间不需要额外的休息时间；在简化范式中，被试者分别进行专注实验和放松实验，考虑到被试者注意力的持续时间有限，每轮专注实验最多30 s，包含30组训练数据，每轮专注实验之前有6 s时间用于休息和准备。由表中可知，随着训练数据量的增加，传统范式和简化范式所需的存储容量都随之增大，但是简化范式所需的存储容量和训练时间都要远低于传统范式。

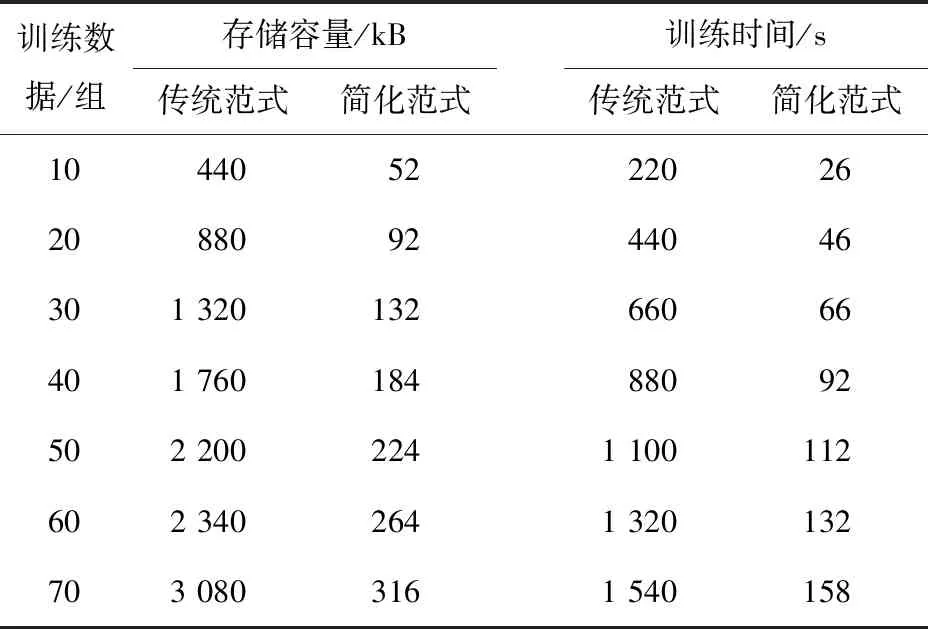
表1 在不同训练数据量下的存储容量和训练时间Tab.1 Storage capacity and training time with different amounts of training data

4.2 参数的选择对系统分类性能的影响

在m=6∶1∶10、τ=5∶1∶10、θ=50∶25∶125不同参数组合下的注意力检测精度数据库中，按照网格搜索循环选取一组被试者平均准确率最高的m,τ,θ的参数组合值(m=8,τ=10,θ=100)。在已知平均准确率最高的参数组合的情况下，依次固定其中两个参数值，相应改变另一个参数值，得到6名被试者在相应参数值 变化下的分类准确率曲线，如图4所示，其中6名被试者分别编号为Subj1、Subj2、Subj3、Subj4、Subj5、Subj6，average表示6名被试者在相应参数值变化下的分类准确率。

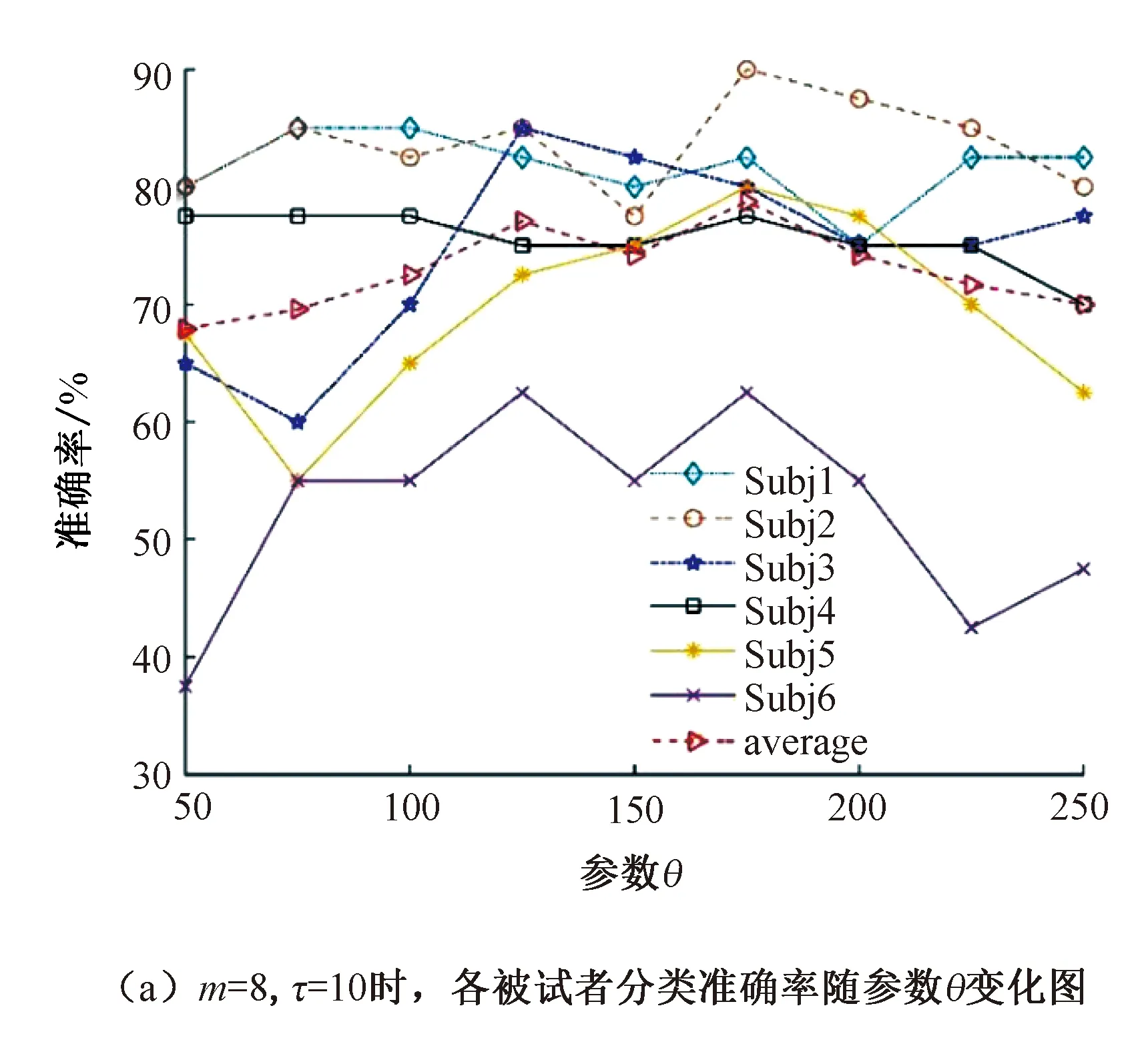
图4 参数变化下的分类准确率曲线Fig.4 Classification accuracy with parameter changes

m=8、τ=10时，在阈值θ变化的过程中，6名被试者的平均准确率最高达到78.75%，最低值是67.92%，平均值达到72.87%；在所有被试者中，随着阈值θ的变化，Subj2达到最高的分类准确率90.00%，Subj6达到最低的分类准确率37.50%。

m=8、θ=100时，在参数τ变化过程中，6名被试者的平均准确率最高达到74.58%，最低值是71.25%，平均值达到72.64%；在所有被试者中，随着阈值τ的变化，Subj1达到最高的分类准确率85.00%，Subj6达到最低的分类准确率52.50%。

τ=10、θ=100时，在参数m变化过程中，6名被试者的平均准确率最高达到76.25%，最低值是70.83%，平均值达到73.00%；在所有被试者中，随着阈值m的变化，Subj1达到最高的分类准确率87.50%，Subj6达到最低的分类准确率55.00%。

分析每个参数组合的最高和最低准确率可以得出：不同的参数会明显引起分类准确率差异。

对6名被试者而言，Subj1在m=6、τ=10、θ=100时最高准确率为87.50%，在m=8、τ=10、θ=200时最低准确率为75.00%；Subj2在m=8、τ=10、θ=175时最高准确率为90.00%，在m=8、τ=8、θ=100时最低准确率为75.00%；Subj3在m=8、τ=10、θ=125时最高准确率为85.00%，在m=8、τ=10、θ=75时最低准确率为60.00%；Subj4在m=9、τ=10、θ=100时最高准确率为80.00%，在m=8、τ=10、θ=250时最低准确率为70.00%；Subj5在m=8、τ=10、θ=175时最高准确率为80.00%，在m=8、τ=10、θ=75时最低准确率为55.00%；Subj6在m=6、τ=10、θ=100时最高准确率为65.00%，在m=8、τ=10、θ=50时最低准确率为37.50%。由此可见，不同被试者的最优准确率参数组合存在差异性。

图4的试验结果显示，当被试者按照传统OCNM算法选取最优参数后，6名被试者的平均准确率为75.80%，而采用本文所述的改进OCNM算法得到平均准确率为72.50%，略低于传统OCNM算法，能够满足在线注意力检测应用的需要。但是对于被试者，使用传统OCNM算法计算一组最优参数大约花费10.76 s(验证平台为搭载i3-7100处理器的笔记本电脑，主频3.9 GHz，内存4 GB，操作系统64位，参数计算的时间包括：计算τ平均7.03 s，计算m平均3.39 s，计算θ平均0.34 s)，而改进OCNM算法的注意力检测过程耗时小于1 s，可以有效降低参数优化所需的时间和计算资源。

4.3 参数的组合对系统分类性能的影响

在已知平均准确率最高的参数组合下固定其中一个参数值，相应改变另两个参数值，得到6名被试者在相应该参数值变化下的三维分类准确率曲线，如图5所示。

由图5进行数据分析可以得出：

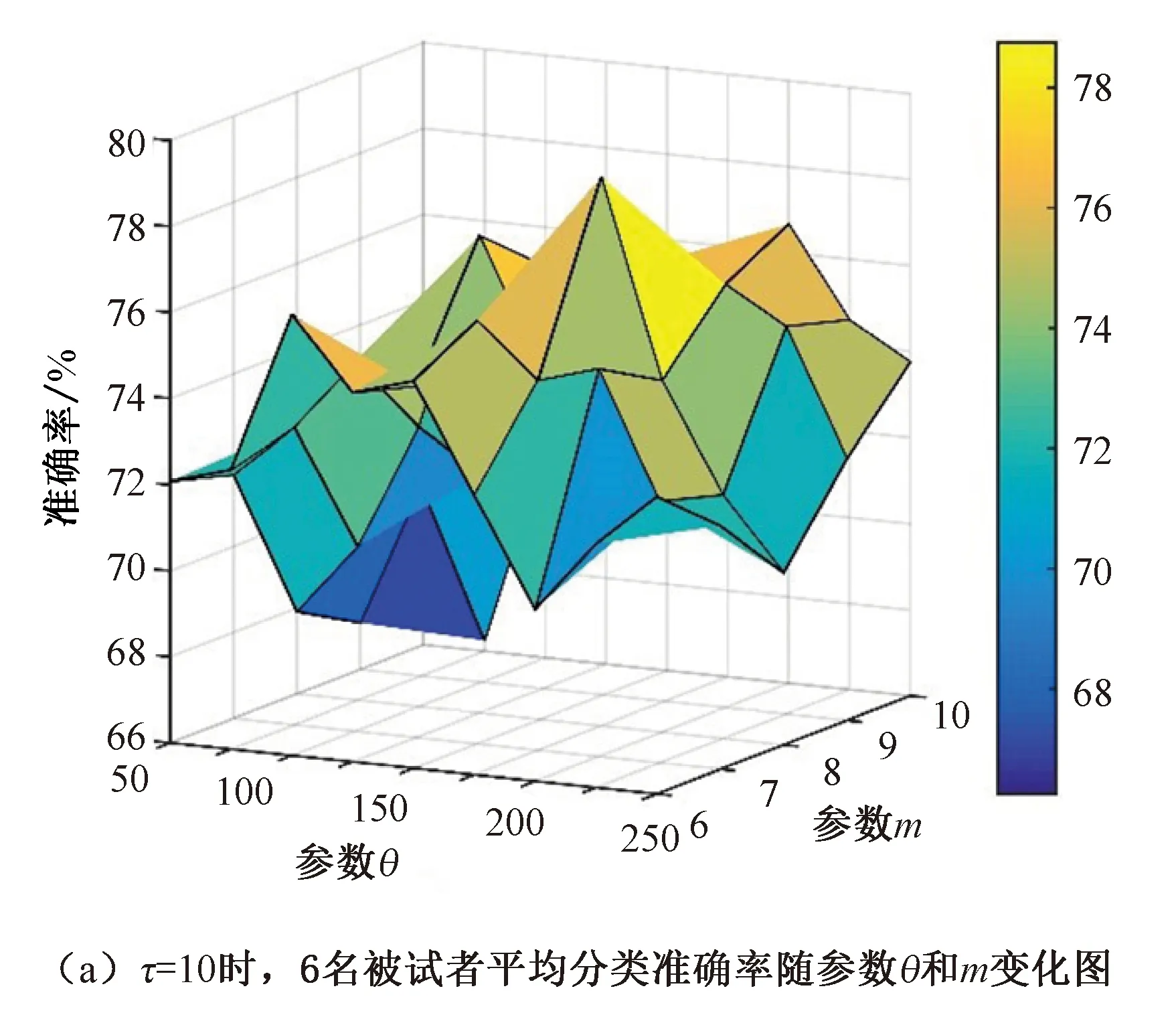
图5 不同参数组合下的分类准确率曲线图Fig.5 Classification accuracy with different parameter combinations

当τ=10时，在参数θ和参数m变化的过程中，在6名被试者中当m=8、θ=175时，最高准确率达到78.75%，当m=10、θ=75时，最低准确率为66.25%。

当m=8时，在参数θ和参数τ变化的过程中，在6名被试者中当τ=9/10、θ=175时，最高准确率达到78.75%，当τ=5、θ=75时，最低准确率为67.08%。

当θ=100时，在参数τ和参数m变化的过程中，在6名被试者中当τ=7、m=6时，最高准确率达到77.50%，当τ=6、m=10时，最低准确率为67.08%。

当选取最优参数组合m=8、τ=10、θ=100时6名被试者的平均准确率达到72.50%，不同参数组合下系统的平均分类准确率不同，选取最优参数值组合符合大多数被试者的分类性能要求，能降低因个体间差异性不同而影响整体准确率。

4.3 基于嵌入式平台的在线验证

表2给出了6名被试者分别使用AMM算法和改进OCNM算法取得的在线试验结果。结果显示在线试验中改进OCNM算法的平均准确率达到了77.78%，相比AMM算法提高了7.20%。

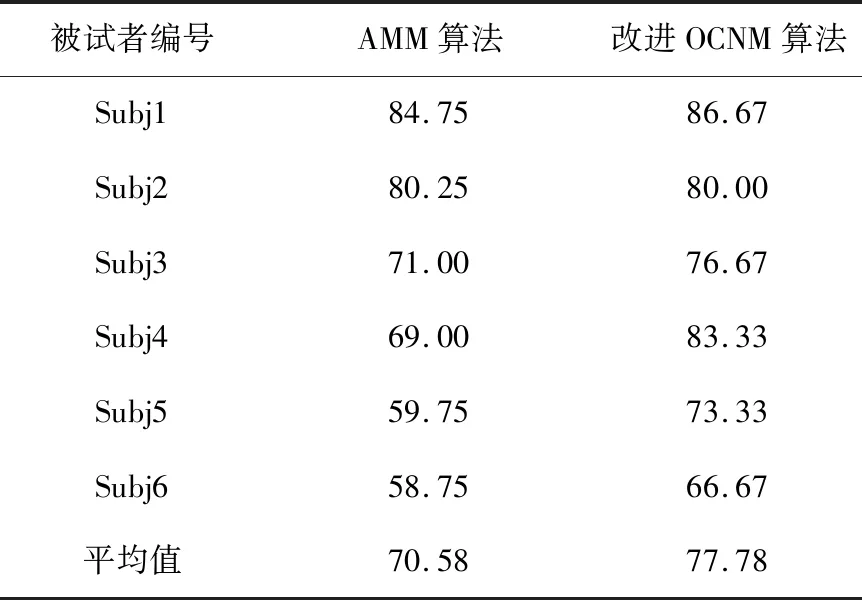
表2 在线试验中不同算法的平均分类准确率Tab.2 Average classification accuracy of different algorithms in online tests %

对于被试者Subj2，两种算法取得了相近的平均准确率(分别为80.00%和80.25%)，而除该被试者外，其余所有被试者使用改进OCNM算法都取得的了更高的平均准确率；尤其对于被试者Subj4和Subj5，改进OCNM算法的平均准确率相比AMM算法分别提高了14.33%和13.58%。

需要注意的是，相比离线试验中取得72.50%的平均准确率，改进OCNM算法在在线试验中取得了更高的平均准确率。一个可能的原因是离线试验截取的是固定时间窗内的脑电数据，这段时间内被试者如果注意力状态出现波动就会输出错误的分类结果。而在在线试验中，被试者可以根据反馈结果调整脑电信号的状态，只要在给出指令后的4 s内输出所要求的状态变化即为分类正确，因而具有更高的平均准确率。

5 结论

针对嵌入式平台存储空间小、计算资源有限的问题，本文提出了一种面向嵌入式平台的脑电信号注意力检测方法，通过范式简化和参数优选，对前期研究中提出的OCNM算法进行了改进。离线试验的结果表明，改进后的OCNM算法将参数计算所需的时间由10.76 s缩短到1 s以内，将被试者的训练时间从880 s缩短到132 s，将训练数据大小从1 760 kB减少到264 kB，而平均准确率相比改进前只是略有降低(从75.80%降低到72.50%)，由此可见，改进OCNM算法在保持较高准确率的同时有效降低了对数据大小和运算时间的要求。本文将该算法在基于STM32F407单片机的嵌入式平台上进行了实现和验证，在线试验的结果表明，相比于当前教育娱乐产品常用的AMM算法，改进OCNM算法在6名被试者上取得了更高的平均准确率。上述试验验证了本文提出的改进OCNM算法不仅能够在资源受限的嵌入式平台上运行，而且仍具有较高的注意力检测精度，故有望用于教育和娱乐领域的相关产品以提升用户体验。