考虑用户行为的电动汽车充电电价制定策略
任丽娜,李相学
(燕山大学 电气工程学院,河北 秦皇岛 066004)
0 引言
电动汽车(Electric Vehicle,EV)接入电网无序充电会加重电网负荷高峰时的负担,对电网运行造成不利影响[1-2]。分时充电电价能够引导车主改变其充电行为,对电动汽车充电进行调度进而减少无序充电带来的不利影响[3]。同时用户自身状态,如用户需电量和电池状态,这些也是用户充电行为的重要参考因素,用户一般会依据自身对电量的需求程度参与电价调度。因此需要分析电价与用户自身状态的关系,进而制定合理的电价策略引导用户充电行为。
目前大量研究将电动汽车调度问题转变为目标优化问题。文献[4]利用蒙特卡洛法对电动汽车在有序和无序充电状态下的充电模型进行仿真,同时设计电网经济性模型并对模型进行优化;文献[5]使用蒙特卡洛仿真建立了电动汽车充放电模型,使用了不同的电价销售方式模拟电网运行,以上文献对电动汽车充电时间的选取只有在傍晚时刻,应在研究中考虑白天充电的情况。文献[6]基于离散吸引力模型建立了多种类型电动汽车充放电需求响应模型,利用遗传算法解出最优电价,但是需求电价模型对每个用户的差异性没有体现。文献[7]针对用户剩余电量和停驶时间等因素进行模糊推理分析并对充电功率进行建模,但不涉及对用户充电行为进行调度。文献[8]设计了针对电网和用户的双层优化模型,但是没有考虑到用户充电行为具有随机性。文献[9]利用电动汽车有序充放电方案改良电网中光伏利用率和负荷波动;文献[10]以实现电网经济性和环保性运行为优化目标设计了电动汽车充放电策略,但以上文献没有分析用户个体的用电行为。文献[11]和[12]研究了在含有电动汽车接入下的电网系统中,如何通过对多个成本函数求和以达到电网总投资最小的规划问题,但是没有综合考虑用户利益影响。
区别于以往在电价调度中使用的电量电价对应关系,本文建立用户充电量与电价和电池状态的对应关系,使得用户可以在考虑到自身电量状态的情况下接受电价调度。本文以通勤用电动汽车为研究对象,通过模糊推理建立用户充电量和电价与剩余电量的关系模型,同时结合影响电动汽车充电总功率的有效因素:充电开始时刻、电池荷电状态和日充电次数,构建电动汽车充电功率模型。以改变电价的方式调控用户在各时刻的充电过程从而控制总体充电量。建立以电网负荷波动最小和用户充电满意度最高为目标的优化模型,使用改进飞蛾火焰算法对电价数值进行寻优,并通过算例验证了模型的可行性。
1 电动汽车充电功率模型
1.1 用户出行规律模型
电动汽车用户使用电动汽车作为上下班通勤的交通工具,根据文献[13]对私人通勤用电动汽车出行情况的统计数据显示,车主上班抵达工作地点和下班后回到家中的具体时间均满足正态分布,其概率密度函数为
f(t)=
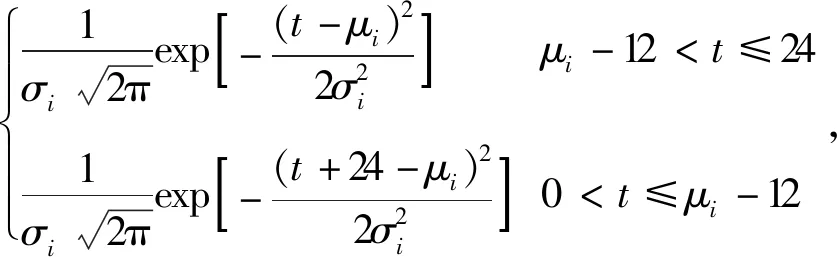
(1)
式中,μi和σi分别表示i时段的期望和标准差;μ1=8.32,σ1=0.85;μ2=19.55,σ2=2.06;i=1表示抵达工作地,i=2表示回到家中;t为时间(h)。
私人电动汽车平均每天出行行驶距离的概率分布密度函数满足如下的对数正态分布,即
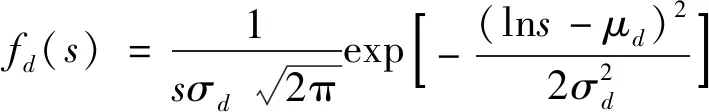
(2)
式中,μd和σd分别表示期望和标准差;μd=3.2;σd=0.88;s为行驶里程(km)。
以上数据显示用户每日通勤出行规律。在抵达工作地或者抵达住宅后,用户可以根据自身情况进行充电[14]。
1.2 电动汽车充电模型
电动汽车的电池荷电状态(State of Charge,SOC)为当前电池电量与电池总容量的比值,是车主决定出行路途距离的重要参考[15],电动汽车电池的荷电状态变化情况表达式为
St=S0-dt/Dmax,
(3)
式中,St为t时刻SOC状态;S0为行程开始时状态;dt为行程开始到时刻的行驶里程;Dmax为电动汽车支持的最大行驶里程(km)。
在到达充电地点后,用户自由选择充电时间。电动汽车用户i的充电时间为
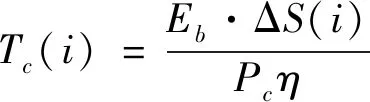
(4)
式中,Tc(i)为用户i的充电时间;Eb为电动汽车电池容量;ΔS(i)为用户i的电动汽车SOC在充电过程中的变化量;Pc为充电桩输入功率(kW);η为充电效率。
结合1.1节中提出的开始充电时间与行驶距离等因素,区域内电动汽车总体充电电量和可以表示为
(5)
式中,PEV为电动汽车总体充电功率;N为区域内电动汽车总数量。
2 基于模糊推理的充电电量模型
2.1 电价设定方式
用户充电电价由电网设定实施,常用种类有固定电价、分时电价、尖峰电价、实时电价等,本文主要考虑分时电价和实时电价两种方式。峰谷分时电价根据一天内不同时刻的负荷差异性,将一天时间划分为峰平谷3个时段,并分别制定对应电价促使用户进行时段选择,合理调配使用方式,改善电网负荷波动;实时电价则是根据时间变化随时对应变化,从而使得用户可以随时进行选择。
传统的工业分时电价设定方式为:以原有固定电价为平时段电价,峰谷时段电价对应上下调整对应比例[16](通常为50%)。此方案具有一定可行性但效果并非最优,本文设定新的实时电价模型对电网系统进行优化,其中实时电价模型公式为
(6)
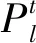
以上实时电价的设定基于分时电价,通过优化变化比例lc,使得电价跟随时间以及固定负载状态对应变化,用户可以在不同时段内获得更多的充电选择。电价变化趋势与固定负载变化趋势相同,例如用户在负载的某高峰时刻因对应的电价较高选择减少充电量,即可达到对总功率曲线进行削峰填谷的目的。
2.2 充电概率模型
在用户到达指定地点允许进行充电时,其充电选择受到多种因素影响,如停驶时间、电价时段、剩余电量、个人心态等。基于本文设定电动汽车作为通勤手段的前提条件下,假设用户在通勤结束后剩余停驶时间充足,即用户充电选择只受到电价和剩余电量的影响。
用户充电行为调整受到主观意愿的影响,且意愿具有不确定性难以量化分析,可采用模糊推理分析用户行为。模糊推理是一种通过分析不精确的前提集合得出对应的结论,进而通过合适的规则去模糊得到问题准确解的方法[7]。本文使用模糊推理对用户充电概率进行模拟,决定用户充电概率的两个因素分别是价格因素和剩余电量。
1)剩余电量
电动汽车的剩余电量是决定用户充电行为的重要影响因素,用户在停驶时的电量应足够下一次出行所需耗电,且此时电量越充足,用户对充电的需求度越小;电量越低,用户充电需求度越大。通过对SOC进行评价作为输入,可以判断用户进行充电的可能性。
2)价格因素
用户充电行为也会受到价格因素的影响,用户做出选择的时刻会处于分时电价对应的某一时段中,分时电价的设定使得用户会对当前时段电价和各不同时段电价进行对比从而做出选择,因此设定Rp表示用户对各时段电价对比后选择的结果,通过与各时段电价相对比,可确定价格因素对用户的影响,其表达式为
Rp=(Cd-Cmin)/(Cmax-Cmin)
,
(7)
式中,Cd为决定时刻电价;Cmax为一天内最高电价;Cmin为一天内最低电价。
将价格因素与剩余电量作为输入,利用模糊推理建立用户的充电概率模型。首先对两个输入进行评价,将剩余电量分为低(Ⅰ级)、中(Ⅱ级)、高(Ⅲ级)三个等级,将价格因素分为低(Ⅰ级)、中(Ⅱ级)、高(Ⅲ级)三个等级,将模糊集排序并选取对应的隶属度函数。根据模糊推理的输出结果,将用户的充电概率分为低(Ⅰ级)、较低(Ⅱ级)、中(Ⅲ级)、较高(Ⅳ级)、高(Ⅴ级)五个等级,并制定模糊推理规则。其中隶属度函数图如图1所示。
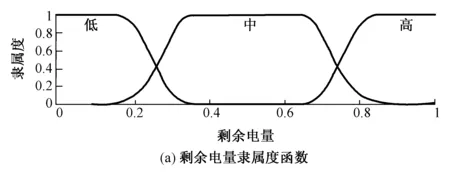
图1 模糊推理系统的各隶属度函数Fig.1 Membership function of fuzzy reasoning system
2.3 充电电量计算
根据不同用户的充电概率,计算其充电电量的期望值,最终将充电电量在时间轴上叠加,即可得到充电电量曲线,具体步骤如下:
1)根据1.1中提出的出行调查数据分析,模拟用户停驶进行充电决策的时间,确定此时电价和用户剩余电量。
2)不同的用户根据自己的电量状态和价格因素进行充电决策,得出概率并与最大充电量相乘计算其对应的充电电量期望。
3)区域内所有用户进行叠加,得到总体充电电量曲线。
3 目标函数及约束条件
3.1 目标函数
电价引导的目的是降低电网波动从而减少其带来的不利影响。本文用负荷方差表示电网的负荷波动情况,同时考虑电动汽车用户的经济性,建立电动汽车充电的电价引导模型[17]。
首先为了使电网的功率波动稳定,选取负荷方差最小为目标函数,以一天24小时进行计算:
,
(8)
,
(9)
,
(10)
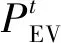
作为电网运行的参与者,还需要考虑用户参与的利益问题[18],首先以用户充电花费节省率最大为目标:
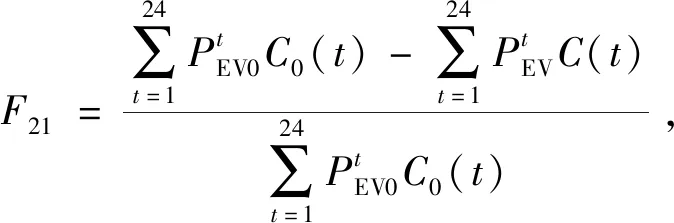
(11)
式中,C(t)表示调度后t时段的充电电价;C0(t)表示调度前t时段的充电电价。
用户为了减少充电花费会减少充电时间,进而导致充电电量的不足,最终影响用户对电动汽车的使用,因此还应考虑用户对电动汽车充电电量的满意度,选择充电电量增加率最大为目标:

(12)
结合以上两者,用户总体充电满意度模型为
F2=μF21+λF22,
(13)
式中,μ和λ表示两个目标的对应权重。
为了解决以上多个优化问题,使用加权系数法将多个目标转化为单目标优化求解,本文设定电网和用户处于平等地位,所以两个目标函数所占比重相等,即求取的总目标函数为
minF=min(F1/2-F2/2)。
(14)
3.2 约束条件
合理的电价制定必须综合考虑参与者双方的各因素影响。具体的约束条件如下:
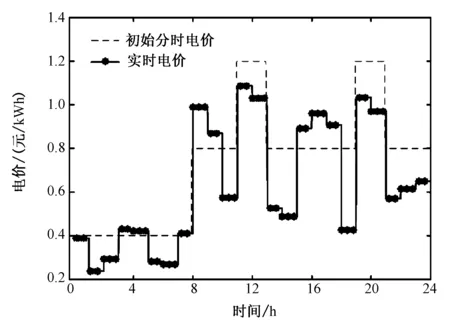
1)实施新电价后,考虑到用户利益和电网收入,电动汽车用户总的充电费用应小于原来的充电费用同时高于下限值:
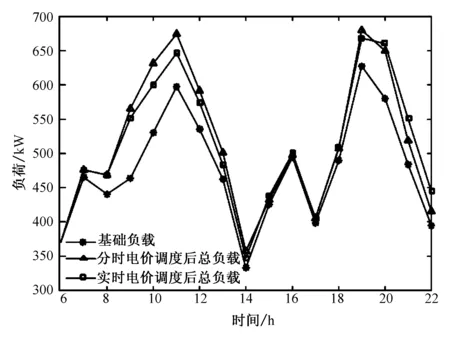
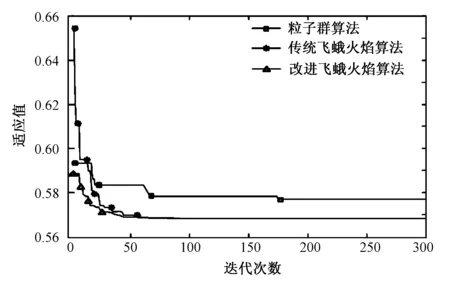
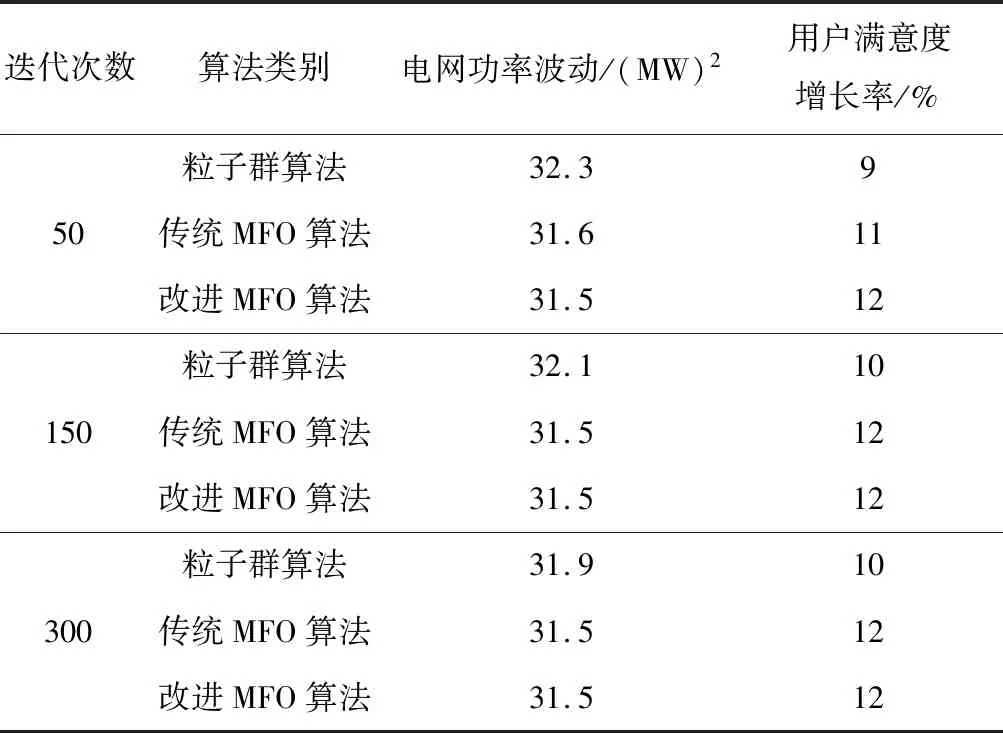
Fc min (15) 式中,Fc为调整后用户总充电费用,Fc0为调整前的用户总充电费用,Fcmin为设定的费用下限值。 2)考虑社会因素影响和峰谷电价的具体设定,电价应指定在约束条件内: Cd,min (16) 式中,Cd,min为设定的电价下限值;Cd,max为设定的电价上限值。 3)调整后负荷曲线的峰谷值应比调整前的范围小,避免出现新的波谷或波峰出现: (17) (18) 4)用户每次充电之后的剩余电量应足够下一次出行消耗: Se>dn/Dmax, (19) 式中,Se为充电结束后SOC状态,dn为下一次出行距离。 1)概述 2015年提出的飞蛾火焰优化算法(Moth-Flame Optimization,MFO)是通过模拟飞蛾寻找火焰时螺旋飞行的运动方式设计的优化算法[19],具有寻优性能好、调节参数少等优点,具备火光位置与飞蛾位置都是最优解候选的双重种群寻优方式,同时飞蛾螺旋形的运动方式增强了搜索速度与准确性,适用于解决本文提出的优化问题。 2)算法数学描述 ① 种群位置初始化:首先对飞蛾的初始位置进行定义,假设n为总飞蛾数,d为空间维数,用矩阵M表示飞蛾群体形成的集合,矩阵其中的每个元素mij表示第i只飞蛾在第j维空间中的位置。定义矩阵O表示飞蛾的适应值集合,其中的每个元素oij表示第i只飞蛾在第j维空间位置对应的适应值。因为火焰位置也为候选解,需要对其进行初始化且原理同上。 ② 位置更新公式:当飞蛾运动进行寻优时,有捕光、弃光两种位置更新方式: 捕光行为:当第i只飞蛾Mi在空间中运动时,会搜索到距离自己最近的火光Fi,并以螺旋运动的方式朝着目标前进,位置更新如下 S(Mi,Fj)=Diebtcos(2πt)+Fj, (20) Di=|Fj-Mi|, (21) 式中,S(Mi,Fj)为第i只飞蛾所在位置;Di表示第i只飞蛾Mi与第j个火光Fi之间的距离;b是螺旋线塑形常数;t为[-1,1]的随机数。 弃光行为:在迭代过程中,飞蛾会逐渐放弃无用火光以加快收敛速度,火焰数量表达式为 (22) 式中,l代表当前的迭代次数;N代表火焰的最大数量;T代表最大迭代次数;round代表对括号内数值取整。 3)算法改进 在飞蛾优化算法中,由于飞蛾螺旋形运动的特征,导致算法的局部搜索能力增强,全局搜索能力减弱,因此在本优化问题中对算法进行如下改动: ① 为了增加算法的全局搜索能力,种群粒子的初始位置由粒子群算法优化得来[20]。粒子群算法作为被广泛应用的智能优化算法,具有全局搜索能力强的优势[21],因此使用粒子群算法初步优化确定种群的初始位置,从而改善初始种群质量,弥补算法搜索中对全局搜索的不足之处。 ② 火焰自衰减是算法为了加快寻优速度的设定,目的是随着算法进行逐渐减少候选的数量。加入火焰衰减自适应系数w,根据所求适应值的变化改变火焰衰减的速度,可以随着算法进行加快衰减,其中w的公式为 w=wmin+(f(i)-fmin)·(wmax-wmin)/(favg-fmin) (23) 式中,wmin和wmax为火焰衰减系数的最小和最大值,分别设定为0.5和1;f(i)为当前迭代次数对应的适应值;fmin为种群适应值的最小值;favg为种群适应值的平均值。 当迭代得到的适应值越接近当前种群的最小值,寻优结果就越接近全局最优,此时火焰衰减速度加快,增加全局寻优速度。改良后的火焰自衰减公式为 (24) ③ 在本文设定的电价调度问题背景下,会出现不合适的电价设定使得调度后的部分数据不符合实际情况,因此应在算法中对优化参数进行约束,一般性飞蛾火焰算法不涉及约束条件的设定,本文考虑约束条件影响,当出现任意时刻不符合实际的情况发生(如电动汽车充电量小于零)时,此时对应的适应度函数值f(c)为 f(c)=f0(c)+E, (25) 式中,E为惩罚因子,通过设定较大的E值使得该组不合适的自变量值在优化过程中被舍去;f0(c)为原适应度函数值。 使用改进飞蛾火焰算法对电价引导模型进行求解的过程如图2所示。 图2 基于优化MFO算法的模型求解流程图Fig.2 Flowchart of model solution using improved MFO algorithm 为验证本文优化模型,以拥有50辆电动汽车的某区域为例,分析该区域在有固定负载和电动汽车接入状态下的电网运行情况,使用本文模型对各时段的充电电价进行优化,同时综合电网运行稳定性和用户利益,对最终电价的制定方法进行分析。 5.1.1参数设定 在仿真中,确定每日11~13、19~21时为峰时段;1~7时为谷时段;其余时段为平时段。其中电价时段设置和固定负载参考文献[22]。为定量分析电动汽车充电工作对电网负荷曲线的影响,设定电动汽车满足以下条件[5-6]: 1)电动汽车型号参考日产LEAF,其参数为车载电池容量Eb=24 kWh,Dmax=160 km,充电功率Pc=3.5 kW,充电效率η=0.9。 2)第一次停驶时SOC状态满足μ=0.6,σ=0.1的正态分布。 3)电动汽车第二次充电的状态为行驶全部路程回家后进行第二次充电。 5.1.2基于模糊推理的充电概率分析 本文使用MATLAB R2018平台进行仿真,将剩余电量和电价因素信号输入Mamdani模糊推理控制器并制定相应的规则(规则制定方式参考文献[7]),通过离线查询的方式得到部分充电概率测试值如下。 如表1中数据所示,用户根据自身剩余电量和所在电价时段综合决定充电概率。 表1 不同输入下充电概率测试值Tab.1 Test values of charging probability with different inputs 5.1.3总体充电量仿真 在初始分时电价作用下,电动汽车充电的日负荷曲线和原固定负载功率曲线图图3所示。 由图3可知,电动汽车充电负荷高峰在早9点与20点左右。在电动汽车接入后,电网峰谷负荷受到了明显影响,峰谷功率差也变大。在原固定负载的波峰段叠加电动汽车充电功率之后形成了更高的波峰,不利于电网稳定运行。 图3 电动汽车充电量与日负载功率曲线图Fig.3 The power curve of EVs charging and fixed load 电网通过制定电价对电动汽车充电行为进行调度,以各时段电价作为自变量通过算法优化得出最优电价制定方式。 仿真中Fc0=18 691;Fcmin=11 214;Cmin=0.2;Cmax=2.2。设定用户对充电电量和费用同等重视,μ和λ分别取0.5和0.5。优化所得电价曲线如图4所示。 图4 电价变化曲线图Fig.4 The curve of different price 初始电价设定方法是以0.8为平时段电价,同时将峰谷电价对应上调和下降50%。实时电价通过优化一天内24 h对应时段系数lc得到,kc值对应各时段原分时电价数值。在原电价的谷时段和平时段,优化电价围绕原电价上下波动;在原电价的峰时段,优化电价有所降低。 图5展示了调度前后电动汽车充电曲线的变化情况,用户总体第一次充电功率明显减少,第二次充电功率提升并且向20时以后的时段转移。在分时电价的背景下,第一次充电总量远大于第二次,实时电价调度平衡了两次充电的总功率,有助于稳定电网总体负荷波动。 图5 电价策略引导下的充电功率曲线图Fig.5 The load curve of the charging power under the guide of price strategy 图6展示了通过了优化电价引导的总负载功率图,固定负载的两个高峰段因为充电功率的加入形成了更高的波峰。经实时电价调度后,11时附近的波峰得到了明显的削减,19时附近的波峰也适当减小,同时20时之后的总功率增加,总体功率波动更加平稳。 图6 电价策略引导下的电网负荷功率曲线图Fig.6 The load curve of the grid under the guide of price strategy 图7展示了使用3种不同算法分析电价最优解时对应的目标函数适应值变化曲线。结果表明:在确定最优电价方案的仿真中,改进的MFO算法收敛速度优于粒子群算法,且粒子群算法陷入了局部最优,而MFO算法在后期迭代中跳出了局部最优;改进MFO算法相对于传统MFO算法有更快的计算速度。迭代曲线显示,改进MFO算法在确定电价最优解的过程中最具实用性。 图7 3种算法的迭代曲线Fig.7 Iterative curve of three search algorithms 通过对3种算法寻优过程中得到的适应值进行比对,得到数据结果如表2所示。结果显示,改进后的MFO算法在求解过程中所得适应值的平均值和最优值均优于粒子群算法,表现了改进MFO算法在求解能力上的优势;同时改进MFO算法在达到最优时所用迭代次数最少,验证了改进算法后寻优速度加快的结果。 表2 3种算法的性能比较Tab.2 Performance comparison of three algorithms 表3展示数据为迭代过程中不同算法对应目标函数的优化结果。结果显示随着迭代进行,电网和用户双方的目标逐渐得到优化;其中粒子群算法在迭代过程中寻优速度较慢,在300次后仍未达到最优解;传统MFO算法在第50次迭代时还未到达最优,寻优速度低于改进MFO算法;改进MFO算法在迭代早期取得了最佳的优化结果,对于改善电网波动曲线和提高用户满意度均有效果,通过改进提高了算法性能。 表3 3种算法在迭代中的优化结果Tab.3 Optimal results by three search algorithms in iteration 表4展示数据为最优电价调度下的结果,其中电网侧功率波动减小;用户侧在适当减少充电电量的同时减少了充电花费,同时总体满意度提高。通过实时电价引导,用户将更多的充电量转移至低功率时段,从而在提高满意度的同时减小了充电成本的花费。电网则在维护用户利益的同时使自身功率波动更加平稳,数据结果显示实时电价调度具有一定有效性。 表4 电价策略引导下的优化结果Tab.4 Optimal results under different price strategy for grid 用户充电行为与电网制定的充电电价的对应关系是电价调度中的重要内容,分析不同用户在不同电价状态下充电行为的差异性有助于调度用户合理充电。本文通过分析用户的充电行为,建立用户充电量与电价和剩余电量关系的模糊推理模型,模型表明用户在不同的电价时段会根据自身的剩余电量做出不同的充电决定;利用此模型设计最优电价制定方案,仿真结果表明,通过该方案调度,实现了减小用户成本和降低电网功率波动的目的;仿真中改进得到的飞蛾火焰优化算法对照仿真中应用的其他算法在快速性和有效性上具有优势。

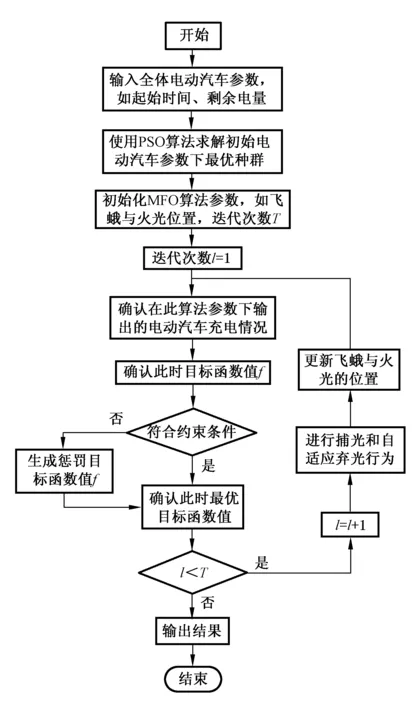
4 算法与模型求解
4.1 飞蛾火焰算法


4.2 模型求解
5 算例分析
5.1 电动汽车充电量模拟


5.2 算法优化结果



6 结论

