船用燃气轮机进气滤清器冲蚀行为研究

翟 斌，卫禹丞，李梦竹，孙海东，柴运强，潘 涛

(中国船舶工业系统工程研究院，北京 100094)

0 引 言

进气系统是燃气轮机的重要部分，用以过滤进气空气，保障燃机安全可靠的运行。惯性滤清器作为进气系统首级过滤装置，会接触空气中的各类杂质，主要包含含盐气溶胶颗粒、固体颗粒等。这些不同粒径、不同含量的杂质颗粒随进气气流通过滤清器，以一定的速度和角度对材料表面进行冲击，使材料出现局部剥落的现象称为冲蚀。冲蚀不仅会使滤清器过滤效率降低，剥落的材料也有可能随气流进入燃气轮机，引起叶轮损坏等恶性故障。冲蚀损伤是不可逆的，更换叶片是消除故障的唯一方法。

典型的惯性滤清器是由带弯钩形疏水槽的曲折叶片组构成，其代表为1940年乌恰斯特金所制作的惯性气水分离器[1]。惯性滤清器由垂直方向排列的“Z”字形金属导流叶片组成，气流沿导流叶片表面流动过程中不断改变方向，夹带的杂质由于惯性较大，运动方向难以改变，从而在撞击金属叶片表面后与主气流分离，脱离空气运动轨迹的杂质流到侧壁上的螺旋槽内，随后流出滤清器。目前，对于惯性滤清器的研究主要集中在优化滤清器结构上，以期在保证分离效率的前提下减小其压力损失。文献[2]基于有限元分析技术，研究了惯性级参数对滤清器性能的影响。文献[3]提出Ω形气水分离器，采用数值模拟和实验相结合的方法分析了其阻力特性及部分工况下的分离效率特性。文献[4]利用数值模拟的方法对U形槽管束惯性分离器的流体动力特性进行了无量纲分析。这些研究对于滤清器分离效率的提高具有重要意义，而随着舰船航行领域的扩大，砂尘等复杂气候条件对于进气滤清器的影响也应该受到重视，砂尘是引起冲蚀最常见的空气杂质。

本文针对冲蚀磨损故障，以典型惯性滤清器叶片为例，基于流体动力学及冲蚀理论，对含砂杂质颗粒空气在惯性滤清器内的运动进行数值模拟，系统地研究空气流速、颗粒质量流量及粒径对冲蚀的影响，以优化滤清器结构，降低冲蚀故障的发生。

1 数值计算方法

1.1 控制方程

进气滤清器内部气流流动特性符合不可压缩粘性流动的纳维-斯托克斯方程，流体材料为忽略质量力，具有常比热容cp以及cv的理想气体，其偏微分方程组表示如下：

连续性方程

动量方程

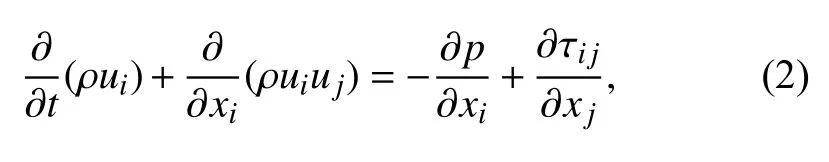
能量方程

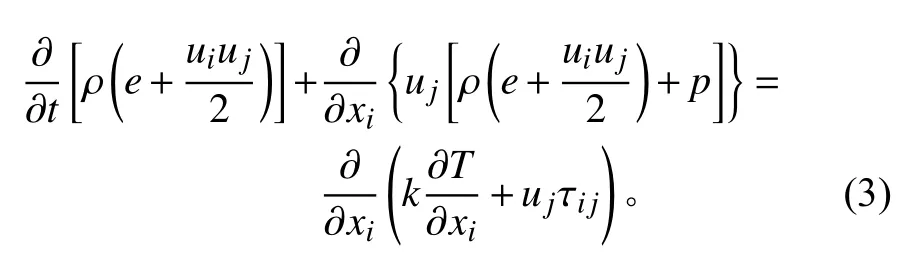
式中：ρ为密度，kg/m3；i,j=1,2,3；xi，xj表示流体质点在流场中的空间坐标；ui，uj表示速度分量，m/s；e为单位质量的内能，J；k为热导热系数，W/（m·K）；T为温度，℉。

1.2 冲蚀模型理论

滤清器壁面冲蚀是由含砂气流中的固体颗粒碰撞壁面引起的，冲蚀速率是与颗粒的碰撞速度，碰撞角度和碰撞次数以及颗粒属性相关的复杂函数。通常冲蚀速率方程可表示为：

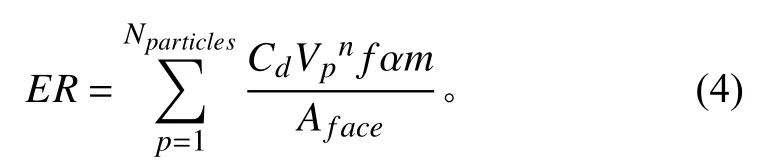
其中：Cd为粒径函数；Vp为颗粒碰撞速度；n为速度指数；a为碰撞角度；fa为碰撞角函数；m为颗粒质量流量；Aface为冲蚀面积；Nparticles为颗粒数量。

在式（4）的基础上，Fluent软件中提供了4种不同的冲蚀计算模型，本文选择Finnie腐蚀模型分析滤清器壁面冲蚀。该模型适用于金属管道壁面的冲蚀磨损，其方程可表示为：

其中：E为基于Finnie 模型的单个颗粒的冲蚀率；k为经验系数，一般取5.83E-7。

Finnie冲蚀模型中的冲蚀速率可理解为冲击到壁面上的颗粒的动能的函数[5]，即n=2，则式（5）可表示为：

其中：

对颗粒的入射角度β、碰撞角度α以及入射速度V、碰撞速度Vp的定义如下：规定初始气流方向与滤清器壁面的夹角为颗粒的入射角度，颗粒运动方向与滤清器壁面的夹角为碰撞角（见图1），与之对应的颗粒速度分别为入射速度和碰撞速度。

通过以上分析可知，单一颗粒对滤清器的冲蚀速率与碰撞速度、碰撞角度有关。滤清器壁面的冲蚀速率是单位面积内所有颗粒冲蚀速率的总和，颗粒质量流量与颗粒粒径通过影响单位面积内的颗粒数量来影响滤清器内的冲蚀速率。

图1 颗粒运动示意图Fig. 1 Schematic diagram of particle movement

2 含砂空气冲蚀滤清器的数值模拟及分析结果

2.1 滤清器内流场结构尺寸及网格划分

以典型惯性滤清器叶型作为参考[1]，基于流体动力学建立惯性滤清器流场二维模型，结构如图2所示。计算域选择3个叶片之间所夹流道，并取延长段，以使进口气流更加接近真实状态。

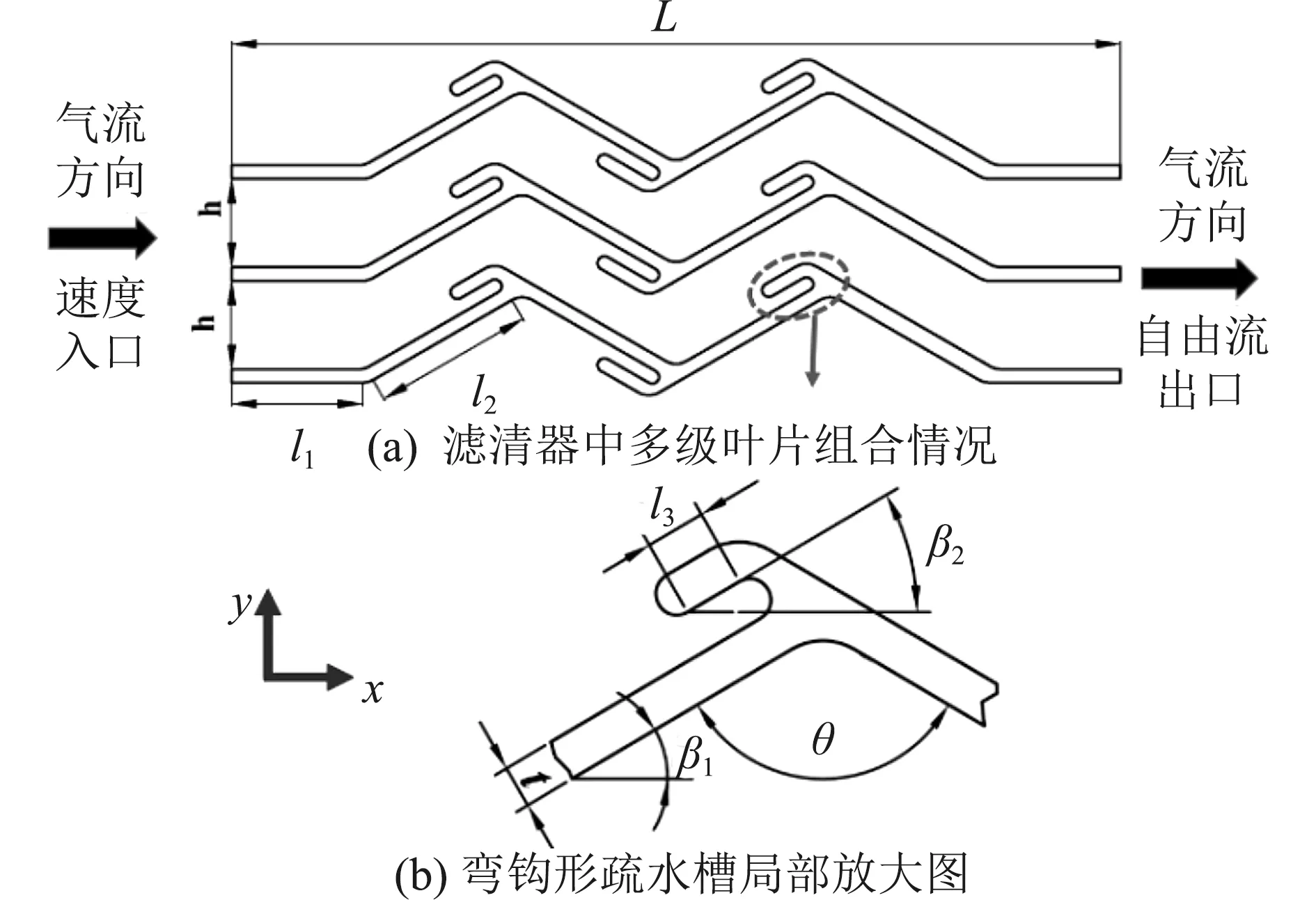
图2 滤清器结构尺寸Fig. 2 Dimensions of filter structure

假设入射气流初始方向始终平行于x轴，且滤清器的安装位置保持不变，则在入口处，颗粒的碰撞角等于气流的入射角等于图2中的β1。在气流进入滤清器内部后，颗粒在碰撞壁面后与气流分离，此时，碰撞角不再等于气流入射角。

本文所采用的滤清器参数如表1所示，网格划分结果如图3所示。模型采用结构化网格和非结构化网格相结合的方法，在结构复杂的弯钩形流道处采用非结构化网格，其余部位全部采用结构化网格，整个模型共有45 417个节点。

表1 滤清器结构参数Tab. 1 Parameters of filter structure

图3 滤清器流场网格Fig. 3 Flow field grid of the filter

2.2 计算模型及边界条件

采用速度入口边界条件，空气入口速度分别设置为V=2 m/s，5 m/s，8 m/s，10 m/s四种工况。出口采用自由流出口边界条件。

入射颗粒材料为石英砂，主要成分为SiO2，密度为2 650 kg/m3。颗粒入射源为面入射源，入射面为气流入口面，颗粒从面上的每一个网格单元中心射入流场，入射速度等于空气速度。滤清器材料为不锈钢。湍流模型采用标准k−ε模型，近壁区采用标准壁面函数法，壁面采用无滑移边界条件[5-7]。速度-压力耦合采用SIMPLE算法，控制方程中的变量和粘性参数采用2阶迎风格式离散。冲蚀率计算模型采用式（6）中石英砂对不锈钢的冲蚀率计算模型。

3 结果与分析

3.1 流场分析

滤清器压力损失及流场稳定性是滤清器重要的性能指标，在降低冲蚀速率的同时需要保证滤清器的压损不会过大，因此，首先对滤清器内速度及压力分布进行分析。

3.1.1 速度分布

不同流速下的速度分布如图4所示。可以看出，流体进入惯性滤清器后，由于惯性级叶片形状的改变及弯钩形疏水槽的存在，使得流场内速度极度不均匀，每个疏水槽的后端以及沟槽内部均存在一个低速区。

为进一步分析流场内速度分布情况，取滤清器中x=0.075 m截面（图4（a）中标示位置），观察速度沿Y轴方向上的变化规律，结果如图5所示。可以看出，两相邻叶片间流场分布一致，且均在靠近壁面区域空气流速最低，甚至发生回流（负值代表沿X轴负方向运动）。2个疏水槽的中间区域的中心位置空气流速最高，且最大速度约为入口速度的2倍左右。同时，随着入口流速的增大，惯性滤清器速度分布的不均匀性增强。

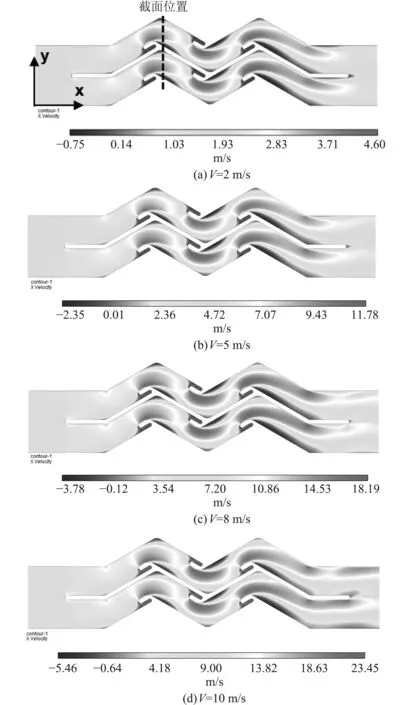
图4 不同空气流速下的速度分布云图Fig. 4 Velocity distribution cloud diagram under different air velocity

图5 不同空气流速下，速度沿Y方向的分布Fig. 5 The velocity distribution along the Y direction under different air flow rates

3.1.2 压力分布

不同流速下滤清器内的压力分布如图6所示。从入口到出口，压力逐渐降低，当流速较低时（≤5 m/s），滤清器内流场压力波动较小，进出口压差较小。当速度从2 m/s增加到5 m/s时，滤清器内压力损失由15 Pa增加到75 Pa。随着入口流速的增加，滤清器内压力波动增大，进出口压差增大。当流速从8 m/s增加到10 m/s时，压差由150 Pa增加到250 Pa。

不同流速下，取滤清器中x=0.075 m截面（图6（a）中标示位置），观察压力沿Y轴方向上的变化规律，结果如图7所示。在靠近下壁面区域压力最高，上壁面处压力最低，同时对比速度分布云图可以看出，在疏水槽后部存在与速度分布的回流区相对应的低压区，有较大的逆压梯度。

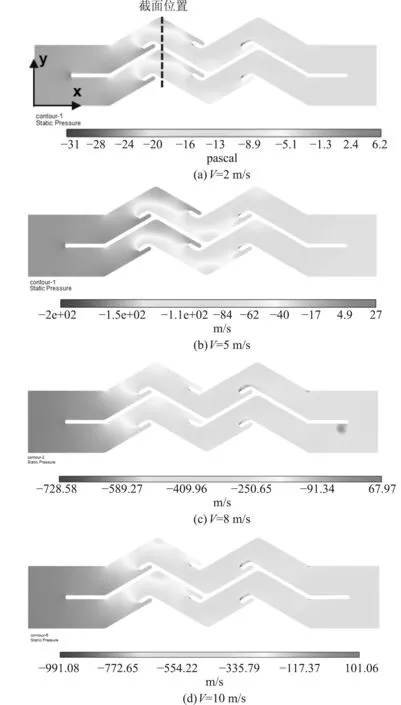
图6 不同空气流速下的压力分布云图Fig. 6 Pressure distribution cloud diagram under different air flow rates

图7 不同空气流速下，压力沿Y方向的分布Fig. 7 Pressure distribution along the Y direction under different air flow rates

3.2 冲蚀影响因素分析

3.2.1 空气流速对冲蚀速率的影响

图8为不同流速下空气中杂质颗粒的运动轨迹图。颗粒在进入惯性级滤清器初期进行直线运动，随后当运动到弯折壁面时（图1中的L2位置）运动方向发生改变，并以一定的动量冲击滤清器的内壁面。由图中不同位置处的颗粒浓度可以看出，无论在何种入射速度下，大部分颗粒将在第1个弯折角及弯钩形疏水槽处撞击壁面后被拦截并返回主气流，据此可推断这2个位置为滤清器内部冲蚀最严重的区域。此外，当入射颗粒质量流量一定时，空气入口流速越高，被拦截的颗粒越多，这与实际状况相符。

为了进一步确定滤清器内的冲蚀情况，对比图9中标注位置处在同一时刻不同空气流速下的冲蚀量，结果如图10所示。

由图10的对比结果可知，当空气流速从2 m/s增加到10 m/s时，第1个折弯角处的冲蚀速度均为最大，与图8的杂质颗粒相的运动轨迹分析结果一致。速度对不同位置冲蚀速率的影响趋势基本相同，入口速度越高，冲蚀速度越大。但在同一水平位置，上下2个流道内的冲蚀速度分布稍有差别，不同位置处的弯折角，冲蚀速率的大小分别为：B-1>A-1，A-2>B-2，B-3>A-3和A-4>B-4。另外，在颗粒质量流量和粒径不变的情况下，冲蚀速率和入口速度的平方成正比，符合Finnie冲蚀模型的计算原理。因此本文仅分析在10 m/s进气速度下，颗粒粒径与质量流量对惯性级滤清器内B-1位置冲蚀速率的影响。

3.2.2 颗粒质量流量及粒径对冲蚀速率的影响

图11为同一粒径下（150 μm）空气流速相同时（10 m/s），颗粒质量流量对冲蚀速率的影响。可以看出，冲蚀速率随着颗粒质量流量线性增加。对于等粒径等密度的杂质颗粒，单位体积内的颗粒数量随着颗粒质量流量的增加而增加。因此，分析颗粒质量流量对冲蚀速率的影响本质是研究单位面积内颗粒碰撞次数对冲蚀速率的影响。同理，颗粒越小，等质量流量杂质中的颗粒数越多，则单位面积内碰撞滤清器壁面的颗粒数越多。因此，当颗粒质量流量一定时，粒径越小，冲蚀速率越高。

图8 不同流速下杂质颗粒相的运动轨迹图Fig. 8 The trajectory diagram of the impurity particle phase at different flow rates

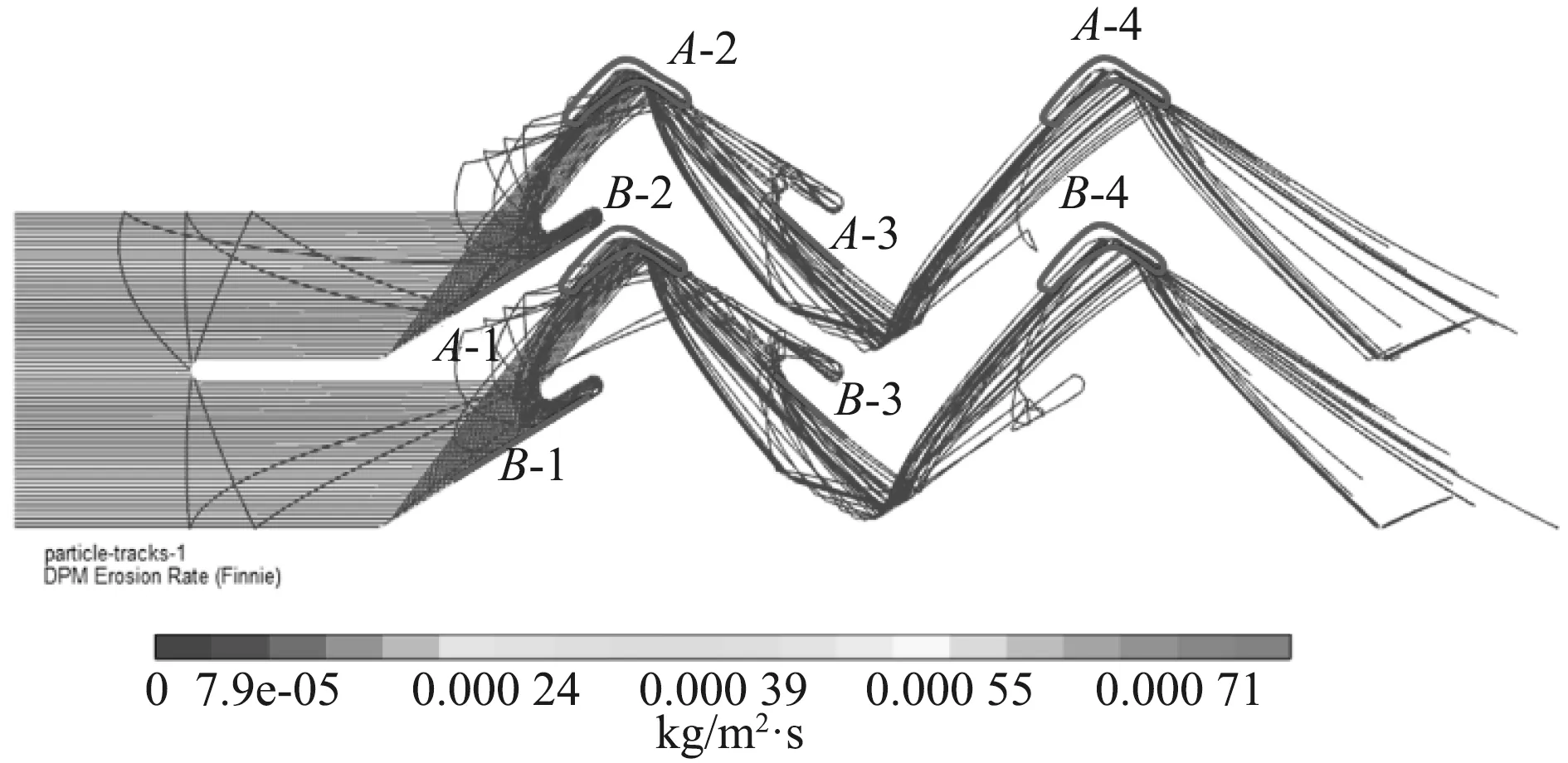
图9 砂粒相的粒子运动轨迹图Fig. 9 Particle trajectory diagram of sand phase

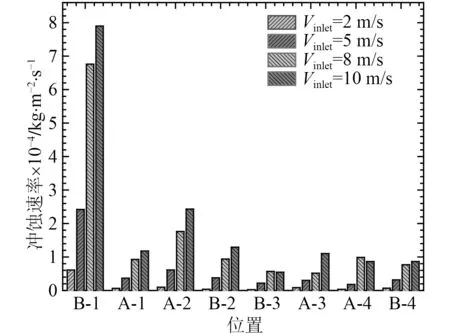
图10 空气流速对不同位置处的冲蚀速率的影响Fig. 10 The influence of air velocity on the erosion rate at different positions

图11 颗粒质量流量对冲蚀速率的影响Fig. 11 The effect of particle mass flow rate on erosion rate

在颗粒质量流量为2 kg/s、空气流速为10 m/s时，不同粒径下，滤清器内的冲蚀速率如图12所示。相比于质量流量对冲蚀速率的影响，粒径对冲蚀速度的影响更为复杂。颗粒数n，颗粒粒径r，以及颗粒质量流量m三者之间的关系可简化为式（8）。可以看出，颗粒数和颗粒粒径的三次方成反比，因此当颗粒粒径增加时，冲蚀速率急剧下降。此外，颗粒粒径也会影响单位面积内颗粒的撞击次数，在一定的空间内，颗粒越小越密集，则单位面积内的撞击次数增大，反之，当颗粒过大时，单位面积内的撞击次数降低。从图12可以看出，当颗粒粒径大于200 μm时，冲蚀速率随粒径的变化幅度减小。

图12 颗粒粒径对冲蚀速率的影响Fig. 12 The effect of particle size on erosion rate

3.2.3 滤清器壁面弯角β1对冲蚀速率的影响

图13为壁面弯角为35°时，空气流速为8 m/s和10 m/s下的压力分布。与图6中当壁面弯角为30°时的压力分布相似，惯性级叶片形状的改变和弯钩形疏水槽影响滤清器内的压力分布。当滤清器内结构参数相同时，进气流速的变化会影响滤清器内低压区的位置及分布，从而改变回流发生的区域。然而，对于本文中提到的滤清器结构，最大冲蚀位置并不受壁面弯折角的影响。这意味着，可以采用局部区域材料优化的方法来提高滤清器的耐冲蚀能力。

图13 不同空气流速下的压力分布云图Fig. 13 Pressure distribution cloud diagram under different air flow rates

在空气流速为10 m/s，粒径为150 μm，颗粒质量流量为2 kg/s时，滤清器壁面弯角β1对冲蚀速率的影响如图14所示。根据结果可知，在β1=25°～30°范围内，冲蚀速率受壁面弯角影响较小，且当壁面弯角为30°时，冲蚀速率最小。当壁面弯角从30°增大到35°时，冲蚀速率大幅增加。

4 结 语

本文采用二维平面模型，基于Finnie冲蚀模型研究了入口空气流速、杂质颗粒质量流量、粒径以及滤清器结构以对冲蚀速率的影响，主要结论如下：

1）杂质颗粒随进气气流进入滤清器后，大部分颗粒在滤清器第1个弯折角及弯钩形疏水槽处撞击壁面后被拦截或返回主气流，因此该区域最易发生冲蚀磨损。最易冲蚀位置与滤清器结构参数及操作参数无关，因为可以通过改变局部区域材料耐磨性能来提高滤清器的耐冲蚀能力。

2）在颗粒质量流量以及粒径一定的情况下，冲蚀速率与入口空气流速的平方成正比；在一定空气流速下，对于等粒径杂质颗粒，冲蚀速率随着颗粒质量流量线性增加；粒径对冲蚀速度的影响较为复杂，在空气流速和颗粒质量流量一定时，冲蚀速率随着粒径的增加而急剧下降，但当颗粒粒径大于200 μm时，粒径对冲蚀速度影响变小。

3）对于本文所采用的滤清器，当壁面弯角β1为30°时，冲蚀速率最小。可采用所提出的二维冲蚀模型确定滤清器在不同工况下的最易冲蚀位置，并对滤清器壁面弯角进行结构优化。

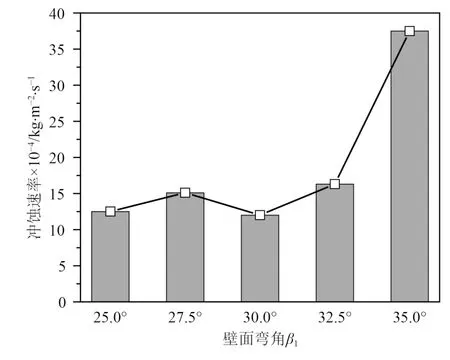
图14 滤清器壁面弯角β1对冲蚀速率的影响Fig. 14 The influence of the wall angle β1 of the filter on the erosion rate