组合预测建模方法在GDP数据预测中的应用
江 安
(安徽文达信息工程学院,合肥 231201)
国民生产总值(GDP)是某个国家在一定时间内生产的所有最终产品和服务价值。它通常被认为是该国经济状况的关键指标。这样,对该国GDP的预测分析至关重要。在GDP预测分析的现阶段,大多数使用单一的预测分析方法。但是单一的预测分析模型仅反映分析对象的部分信息,如果使用不同的方法来进行仿真模拟,虽然能各有所长,但存在取舍难题。如果使用几种类型的预测分析方法的线性组合来生成预测模型,则不仅可以开发各种预测分析方法提供的有利信息,提高预测分析的准确性,而且可以描述目标的客观内容,取精华,弃糟粕。本文以最小误差原则构建的组合预测模型对我国2015年各季度GDP进行预测,效果优于三个单项预测模型。
一 灰色预测模型
GM(1,1)模型是最常用的一种灰色模型,它常用于时间序列数据的预测。设GDP数列

构成灰色模块微分方程
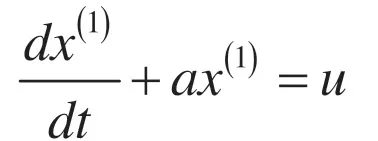
将灰参数代入得时间函数

根据累加序列的预测结果进行减法运算,推算出原始序列的预测值:

表1为基于灰色预测模型利用Matlab求得1992年至2015年的GDP预测结果和预测误差。

表1 中国GDP灰色预测方法的预测结果和预测误差(单位:亿元)

续上表
由表1可以得知利用灰色预测模型进行预测的结果产生误差较大,而且存在很大的波动性,有些预测值偏离过大,最终导致其预测的结果精度不高。
二 ARIMA预测模型
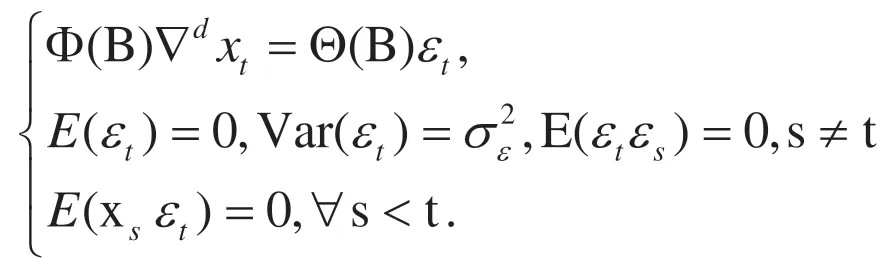
从表1可以得出中国各季度GDP单季值的变化趋势,如下图:
由图1可以知道,中国GDP各季单季值一直保持明显的增长趋势,在ARIMA模型中,GDP序列非平稳,为了使该时间序列更容易变得平稳,先对序列GDP取对数,令,观察发现两阶差分后该模型变得平稳,然后再进行拟合。

图1 中国GDP各季度单季值
表2为基于ARIMA预测模型利用Matlab求得1992年至2015年的GDP预测结果和预测误差。

表2 中国GDPARIMA预测方法的预测结果和预测误差(单位:亿元)
由表2可以知道,刚开始的预测误差较大,后来预测精度逐渐提高,说明了其预测值受近期的影响较大,受远期的影响较小,其相对于灰色预测模型对全国GDP的预测精度有一定程度的提高。
三 多项式趋势拟合模型
设变量表示时间序列,建立与时间趋势的多项式预测模型:
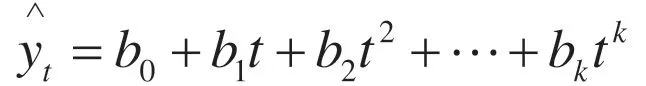
表3为基于多项式趋势拟合模型利用Matlab求得1992年至2015年的GDP预测结果和预测误差。
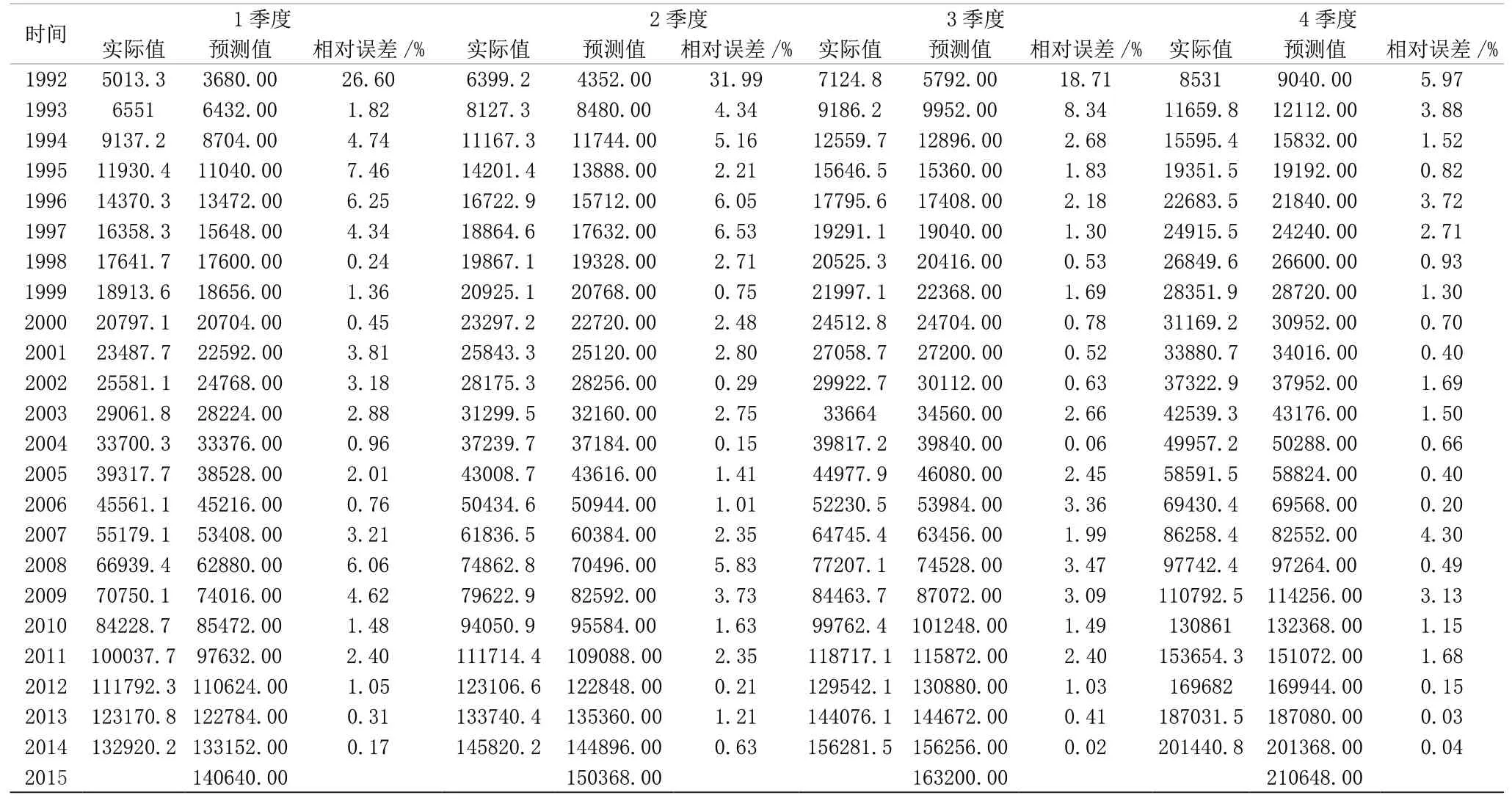
表3 中国GDP多项式趋势拟合方法的预测结果和预测误差(单位:亿元)
由于全国GDP具有较明显的增长趋势,运用多项式趋势拟合的对趋势的把握比较准确。从表3的数据分析中也可以得出采用多项式趋势拟合对全国GDP的预测误差较小。
四 组合预测模型
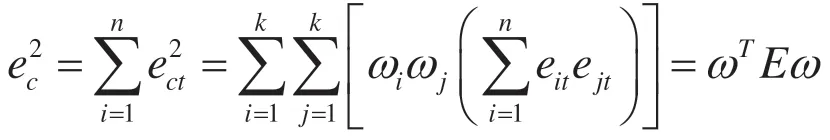
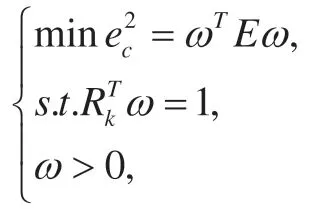
利用Matlab进行求解得到以上三个模型的最优权值分别为:

故可得各种预测模型的结果的对比如表4:
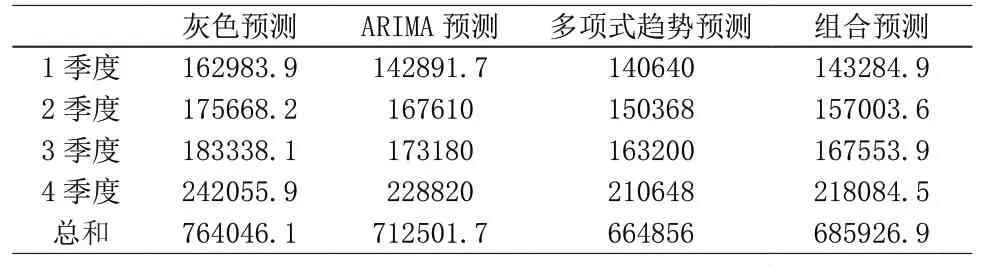
表4 2015年中国GDP各季度预测结果(单位:亿元)
我国2015年GDP总和实际为685506亿元,本文组合预测模型的预测相对误差为0.0007,远远小于灰色预测的0.1146、ARIMA预测的0.0394、多项式趋势预测的0.0301,有很好的预测效果。
五 结束语
本文的组合预测模型既吸收了单项模型的特点,又探讨了其他的相关因素,因此其预测结果可信度更高。在实际应用中还应注意到,组合预测模型的预测精度主要取决于各个单项模型的好坏,因而应力求提高单项模型的预测精度。总之,组合预测模型具有比其他单项模型更好的优势,结果更接近于真实数据,精度较好,还可应用于其他时间序列数据的预测。

