一种基于改进遗传算法的宽带吸波材料优化设计方法

邢正维,梁迪飞,刘 川,刘 倩,李健骁

(电子科技大学 国家电磁辐射控制材料工程技术研究中心,四川 成都 611731)

随着雷达探测技术的快速发展,其对己方军事目标的威胁已经越来越大。先进的吸波材料应满足厚度薄、重量轻、吸收带宽宽、吸收能力强的要求[1]。传统的单一吸波材料因吸收峰单一、吸波频段窄而难以满足当前宽带的吸波性能需求。而多层吸波材料可以将各组分材料的性能互补和关联,在很大程度上拓宽了吸波带宽,可获得单一材料所不能达到的综合性能[2-3]。目前的研究主要采用多层传输线理论或多层均匀平面分层介质理论,结合计算机辅助设计多层吸波材料。采用的优化算法主要有:遗传算法(GA)[4]、粒子群优化算法(PSO)[5]、差分进化算法(DE)[6]、蝴蝶优化算法(BOA)[7]、人工蜂群算法(ABC)[8-9]等。尽管很多研究人员在多层优化的问题上尝试了不同的优化算法,但优化中间结果的适应度评估函数还是采用了均值、平方求和、权重系数法等[8-11]。这些设定的适应度函数并不能很好地反映优化的需求,如:权重系数法的权重系数设定就对优化的结果影响很大,而且难以找到一个适用于所有优化目标的权重系数。目前的多层设计研究更趋向于研究算法的寻优能力,而忽略了将吸波优化需求转化为合理数学模型的重要性。事实上影响吸波优化设计结果的不仅仅是算法的寻优能力,优化需求的数学模型转化即适应度函数也很重要。

本文的适应度函数依据优化的目标带宽和最小反射损耗定义,能很好地反映真实的优化需求。针对带宽和厚度的多目标优化,引入了优化设计总厚度和带宽均衡的措施,即可以选择牺牲一些吸波性能来降低优化设计的总体厚度。基于遗传算法结合上述改进可以很好地优化出符合需求的结果,并通过优化一个带宽2～18 GHz、最小反射损耗-10 dB 的多层设计实例进行验证。

1 结构与原理

1.1 多层吸波材料优化设计的结构与理论

多层吸波材料优化设计的结构如图1 所示,均匀平面波垂直入射到多层吸波材料表面,中间的N层为吸波材料,底层为金属板。根据电磁波的等效传输线理论可等效为图2 所示的N段不同的均匀传输线级联的电路模型[12]。

图1 多层吸波材料结构示意图Fig.1 Schematic diagram of multilayer absorbing material structure

图2 等效传输线电路模型Fig.2 Equivalent transmission line circuit model

依据等效的电路模型最终可以递推地求解出多层吸波材料的等效输入阻抗。其中从第k层看进去的等效输入阻抗采用如下公式计算:

式中:Zink表示第k层吸波材料的等效输入阻抗;Zin(k-1)表示第(k-1)层材料的等效输入阻抗;Zk表示第k层材料的波阻抗;dk为第k层材料的厚度;μrk为第k层材料的相对磁导率;εrk为第k层材料的相对介电常数;f为频率;c为光速;为空气的波阻抗,μ0和ε0分别为真空的磁导率和介电常数。第0 层的材料为金属可当作理想导体,因此其特性阻抗为Zin0=0。递推求解出多层吸波材料的等效输入阻抗后,可依据下式计算出多层吸波结构的反射率:

1.2 数据库材料的吸波特性

吸波材料的吸波性能主要由磁性吸收剂羰基铁粉、铁硅铝等的特性决定。多层吸波材料的吸波性能跟每一层材料的吸波特性相关。因此针对设定的优化目标,需要数据库的不同材料具有交叉覆盖全频段的吸波性能。本次优化使用的数据库参数包括羰基铁粉和铁硅铝与石蜡不同比例混合制环测得的电磁参数。依据公式(1)简化的单层反射率计算模型可计算对应的反射率,得到的球形羰基铁材料厚度为2 mm 具有的吸波性能如图3 所示。

图3 羰基铁吸收剂不同比例反射率Fig.3 Reflectance of different ratios of carbonyl iron absorbent

可见随着吸收剂比例的提高,反射率的吸收峰向低频移动,铁硅铝也具有此类规律。此外同一种材料比例一致时,随着厚度的增加,反射率峰值也向低频移动,如图4 所示。

图4 羰基铁吸收剂同种比例不同厚度反射率Fig.4 Carbonyl iron absorber with the same proportion and different thickness reflectivity

因此选用不同种类和厚度的材料进行多层设计,理论上是可以拓展吸波带宽的。此外依据文献[13]所述,为了实现某一吸波带宽的某一设定反射损耗,基于材料的性能有一个极限的最小厚度。因此在给定优化目标和数据库之后,多层优化设计展宽带宽有一个上限。这个上限由材料库材料性能、优化目标频段、总厚度约束、最小反射损耗所共同决定。

2 遗传算法优化设计

改进后的遗传算法优化设计流程如图5 所示,下面给出具体的设计分析。

图5 遗传算法优化设计流程图Fig.5 Genetic algorithm optimization design flow chart

2.1 编码方案设计

采用二进制对多层材料进行种类和厚度的编码,种群中的每一个个体的染色体编码形式为S1D1S2D2…SiDi…SnDn。其中Si代表第i层材料的种类编码,Di表示第i层材料的厚度编码,两者组成的二进制串SiDi就是第i层材料的编码。每个个体二进制编码的总体长度依据材料库的材料种类、单层材料设计的精度(单层厚度保留的小数位数)和单层上下限厚度确定,其公式为:

式中:L1表示编码材料种类需要的二进制位数;M表示数据库材料种类;L2表示编码单层厚度需要的二进制位数;dmax与dmin分别代表每层材料厚度的上限与下限值;S表示单层厚度保留的小数位数;K表示优化的总层数;L表示每个个体二进制编码总长度。

2.2 适应度函数设计

适应度函数是用来评估种群中个体优劣程度的主要指标,因此适应度函数设计的好坏将直接影响到遗传算法能否找到满足优化需求的最优解。多层设计的目的是要得到宽带的吸波优化结果,因此适应度函数必须要能正确的评价个体中宽带和窄带吸波的设计结果。为此采用如下的适应度函数:

其中S1和S2如图6 所示,S2为红色框选的长方形部分的面积,S1为红色框选的长方形内部的填充面积,采用微元求和的方法计算,具体计算公式如下:

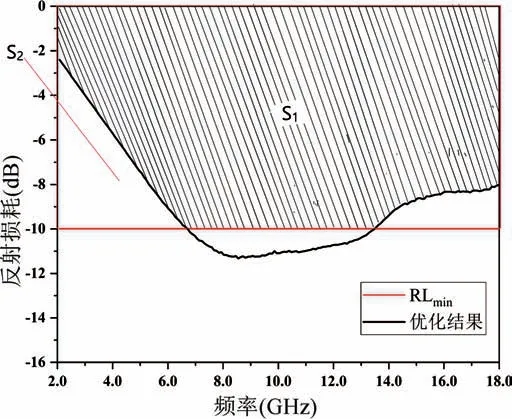
图6 适应度函数示意图Fig.6 Schematic diagram of fitness function

式中:R(fi)表示对应频点fi处的反射率值;RLmin表示优化设定的最小反射损耗。适应度值反映了红色框选部分的填充比例,其值域为[0,1]。

2.3 算法的优化改进

多层吸波材料优化设计不仅要求优化的结果尽可能地满足优化目标,同时也希望优化结果在不超过总厚度约束的情况下尽可能薄。但吸波材料的“薄” 和“宽” 是两个冲突的要求,为此引入了设计总厚度和带宽的均衡措施,能对适应度值进行修正。即在优化开始前可以设定厚度约束参数(0 或1),来选择本次优化是否需要牺牲一些吸波性能降低总体厚度。修正的具体步骤如下:(1)找到种群中适应度值最大的个体,将其适应度值和总厚度作为标准;(2)对小于最大适应度值某一范围的个体,计算其与最大适应度个体厚度和适应度的差值,然后分别归一化;(3)将总厚度和适应度的归一化差值相减,然后加在各自的适应度值上。

为了避免适应度值最大个体在遗传进化的过程中,被交叉和变异运算破坏,采用了精英选择策略。将历代适应度值最大的个体进行复制保留,待到交叉变异结束,用复制保留的个体替换掉种群中最差的个体,然后进行下一代遗传操作。此外遗传算法具有容易陷入“早熟” 的缺陷,为此引入了种群多样性评估,包括个体外部多样性评估和种群整体多样性评估,分别用来评估种群个体间的差异程度和种群整体的多样性程度[14]。个体外部多样性的计算公式如下:

种群整体多样性的计算公式如下:

式中:pij表示种群中个体i的第j位二进制值;NP 表示种群大小;L表示每个个体二进制编码总长度。

2.4 选择、交叉、变异的设计

遗传算法的进化过程中,对种群个体的选择采用无放回余数随机选择,而没有完全采用基于适应度值的概率选择。保证了适应度值高的个体能够被遗传到下一代,降低了选择误差[15]。无放回余数随机选择的过程如下:

(1)计算种群中各个个体在下一代种群中的期望值:

(2)用Ni的整数部分去确定各个对应个体在下一代种群中的数目,由该步共可以确定出下代种群的个个体。

(3) 调整个体的适应度值为:Fi -[Ni]×,种群中的剩余个体采用基于适应度值的概率选择(轮盘赌策略)来随机确定。

交叉采用随机配对的均匀交叉,先对种群中的个体进行随机选择两两配对,然后两两进行基于交叉概率的交叉。变异则采用基于变异概率的基本位变异。

3 结果与讨论

基于上述优化设计流程进行优化设计,各遗传参数的设置如下:

材料库材料种类:T=18,种群大小:NP=500,迭代次数:G=200,交叉概率:Pc=0.8,变异概率:Pm=0.01。

设定的优化目标参数:优化频段:2～18 GHz,最小反射损耗:RLmin=-10 dB,单层设计厚度保留小数位数:S=2,设计总厚度约束:2 mm,然后设置不同的层数限制进行优化。不同层数未施加厚度约束和施加厚度约束的优化设计结果如表1。

由表1 可见在无厚度均衡2 mm 总厚度约束下,优化结果适应度最大值为20 层的0.967,其总厚度为1.980 mm。

表1 不同层数有(无)厚度均衡的优化结果Tab.1 Optimization results of different layers with(without) thickness balance

将有(无)厚度均衡的优化数据作图,由图7 可见无厚度均衡优化结果在层数较少和较多时,适应度值和总厚度的曲线增减趋势并不同步,在厚度增加或者下降较大时,适应度值并未有相应比例的增加或者下降。而在20 层左右的中间段,适应度值和总厚度的曲线增减趋势符合较好,因此该区间段的优化结果更接近于对应材料库性能、所设优化参数能优化出的结果极限。

图7 有(无)厚度均衡优化结果对比Fig.7 Comparison of optimization results with(without) thickness balance

有的时候为了尽可能减少设计的总厚度,可以适当牺牲一些目标频段的吸波性能。为此引入了厚度均衡措施,图7 也给出了2 mm 总厚度约束下有均衡措施和无均衡措施优化结果的适应度值、总厚度对比,均衡措施调整适应度值的范围是种群中适应度值前10%的个体。由优化结果可见取得了一定的效果,能在适应度值减小比例不大的情况下,让总厚度得到降低。如:33 层的优化结果总厚度下降了约0.4 mm,而适应度值(填充度)仅下降约0.06。此外不同层数优化结果用到的材料种类变化如图8,可见随着吸波优化设定层数的增加,吸波优化结果用到的材料种类也会有一定的增多。

图8 无厚度均衡优化使用材料种类Fig.8 Optimal use of materials without thickness balance

图9 给出了20 层有(无)厚度均衡措施的优化结果反射率对比,两者的适应度值分别为0.967 和0.925。可见加入厚度均衡措施后的优化结果在适应度值上有所下降,减小的主要是低频部分。所以可以预见在要求厚度较薄的情况下,多层吸波材料优化设计也难以实现低频部分的吸波性能优化。

图9 20 层有(无)厚度均衡优化结果反射损耗Fig.9 20 layers with (without) thickness balance optimization result reflection loss

20 层无均衡措施的优化过程中种群整体多样性和个体外部多样性的变化分别如图10 所示。可见两者在整体上均呈现为下降趋势,且个体多样性还伴随有波动,这主要是种群的交叉和变异所引起的个体多样性变化。而种群的整体多样性仅受变异的影响,因此波动很小。说明交叉和变异有利于防止过早收敛,在一定程度上保证了种群中个体间的多样性。

图10 (a)个体多样性变化;(b)整体多样性变化Fig.10 (a) Individual diversity changes;(b) Overall diversity changes

另比较了在相同厚度(1.99 mm)下多层优化结果和优化中用到单一材料的反射率。此处选择10 层的优化结果进行对比,其多层优化结果用到的材料种类为7 种。对比结果如图11(图中#数字表示优化数据库中材料对应的编号),可见多层优化结果的-10 dB 吸波带宽优于任一单一组分材料。因此多层设计有利于拓展吸波带宽,但同时也可以看到其没有了单一组分材料的吸收峰。所以多层设计为了拓展吸波带宽也会牺牲部分频段的一些吸波性能。

图11 10 层优化结果与单一材料反射损耗对比Fig.11 Comparison of 10-layer optimization results and single material reflection loss

4 结论

本文基于改进的遗传算法进行多层吸波材料的优化设计,用优化区间的填充量定义适应度函数,最终优化得到了符合目标需求的优化结果。并通过对优化结果的分析得到了以下结论:(1)针对某一优化目标,多层吸波设计的层数并不是越多越好,最佳的层数取决于材料库的材料性能和优化的目标;(2)好的多层吸波设计对比同厚度单一材料,能有效拓展吸波带宽;(3)在相同厚度下对比多层和其单一组分的吸波性能可以发现,尽管多层设计拓展了吸波带宽,但也牺牲了部分频段的吸波性能;(4)在要求厚度较薄的情况下,多层优化设计也难以实现宽带的低频吸波效果。