基于收费数据的高速公路收费站通行能力分析
李君羡,周一晨,高志波,沈宙彪,吴志周
(1.同济大学 道路与交通工程教育部重点实验室,上海 201804;2.上海耐特高速公路收费结算有限公司,上海 200063;3.上海市城市建设设计研究总院(集团)有限公司,上海 200125)
0 引言
根据2019年国务院《政府工作报告》,我国将在两年内逐步升级高速公路收费设施以推广ETC(Electronic Toll Collection,电子不停车收费)。届时各收费站将同时包括ETC与MTC(Manual Toll Collection,人工半自动收费)两类车道,后者实际提供ETC,MTC两种收费服务。升级后收费站的通行能力将发生变化[1]。
收费站通行能力分析是收费站服务评价和资源配置优化的基础工作,也是学界关心的热点问题。早期因数据资源匮乏,仿真模拟是研究这一问题的重要手段:Li[2]、李剑等[3]借助仿真分析混合交通流下ETC车道的通行能力;Zhang等[4]基于仿真讨论ETC车道位置对其通行能力的影响;Liu等[5]针对特定收费站,通过仿真得到其配置不同数量ETC/MTC车道时的整体通行能力。也有研究把仿真作为理论建模有效性的验证工具:崔洪军等[6]基于车辆最小间距计算理想状态下ETC车道的通行能力并以仿真校验;王慧勇[7]提出收费站整体通行能力的计算方法并以仿真测试其效能。上述研究涉及收费站土建设计方案、交通流特征相关的大量仿真参数标定工作,复杂度高,而面向特定场景精确调参仿真模型又局限了场景特征,导致结论适用范围受限。
为此,其他学者主张融合排队论和交通工程理论,提出不同车道配置场景下收费站通行能力的计算方法。许多成果尤其侧重对ETC车道的研究:Amorim等[8]以收费站收入最大化为目标提出收费站建设方案决策模型,讨论了ETC车道位置对其通行能力的影响;Zarrillo等针对不同服务场景提出了ETC车道通行能力的计算方法[9],并以实例验证了该算法的准确性[10];廖固[11]讨论了不同需求和供给条件下ETC车道的通行能力变化;罗梓铭等[12]提出了由ETC车道与主线相对位置决定的ETC车道通行能力折减系数;程俊龙[13]基于平均延误将ETC通道的服务水平划分为5个等级,并计算出各等级的最大服务交通量。
目前我国ETC和MTC模式并存,兼顾二者考虑收费站车辆通行行为进而研究其通行能力的成果更有借鉴意义。Levinson等[14]提出了一个支付选择模型,描述用户选择缴费方式的决策模式;Kim[15]不区分收费模式,结合M/G/1排队过程与非线性整数规划,通过灵敏度分析评估交通量增加对通行能力的影响,提出了车道规划方案的优化方法;Komada等[16]证明了两类收费车道的基本图与两类车辆的密度和比例有强相关性,从而支持不同类型车道的通行能力计算;罗梓铭[17]基于我国收费站混合收费模式,考虑交通量、ETC使用率、车道总数等约束,提出车道配置方案最优化方法,综合提升混合收费站的总通行能力。
具有启发意义的是,许多学者将通行能力估计问题转化为单车服务时长分析问题展开研究。周刚[18]基于收费站过车延误分析通行能力;Boronico等[19]结合运营成本和用户成本研究车道配置,采用随机排队模型讨论不同时段下两类车道的平均服务时长;Murat等[20]考虑付费时长、过车类型组成、广场引道几何结构、车道使用和车辆物理特性,计算收费站3种交通状态下的过车延误;Navandar[21]等将收费站车流通过行为划分为7类,提出根据引道交通量和交通组成确定车辆类型服务时间的方法。鉴于服务时长在实际操作中更易观测和验证,并便于引入分布描述,这类研究为通行能力计算提供了良好的思路。
以上研究的出发点均基于理论建模,辅以仿真或单体收费站的短期数据验证,强调微观参数的调试并伴随诸多假设,可靠性不及数据驱动方法。随着我国ETC车道数量大幅提升,MTC车道数据采集能力也有所改善,由此产生的全量收费车道过车记录为收费站通行能力研究提供了“富信息环境”。相比视频数据,这类信息不受设施位置、恶劣天气和不利光照条件的影响,且为结构化数据,对存储和算力要求很低,可满足在线分析要求。本文即基于真实过车收费数据以避免理想化假设和多目标复杂模型构建,综合考虑未来收费站混合交通流、两种收费模式并存的条件,借鉴以服务时长为切入点的方法,研究收费车道的通行能力及其影响因素。
1 数据及预处理
截至2020年9月,上海市所有收费站入口ETC过车占比70.1%,出口占比67.0%,部分收费站高峰期间常发拥堵,为研究车道饱和通行能力提供了良好的数据条件。以日均流量大、排堵难度大为条件选取上海市具有代表性的4个收费站:G15沪翔高速、G2江桥、G60新桥主线及G50徐泾收费站(下分别称为1~4号收费站),收集其2020年8月3日至8月16日计14天内逐条过车数据作为研究基础。
每条数据包括以下5个字段:(1)精确到秒的收费时刻t(抬杆前费用计入系统的时刻);(2)过车所在车道类型F={e,m}(e为ETC车道,m为MTC车道,后者提供两种收费方式);(3)过车车道编号l;(4)过车车辆类型C;(5)过车实际收费方式W={E,M}(E为ETC收费,M为MTC收费)。
数据预处理工作包括:(1)免费通过收费站的各类车型综合占比0.30%,为免干扰计算结果,将其剔除;(2)为降低存储要求及后续分组运算复杂度,将F,C,W属性各自编码为整型标量存储;(3)将所有过车数据按日期、收费站和车道分组,每组为特定日期指定收费站某车道过车记录集合。将各组数据按t从早到晚排序,以式(1)计算每条过车数据对应的间隔时长ts:
tsi=ti-ti-1,
(1)
式中,tsi为第i条过车记录的间隔时长,即[ts]序列中第i个元素;ti和ti-1分别为当日第i和第i-1条数据对应的收费时刻。各车道ts0由当日第1条数据和前日最后一条数据计算得到。因原始数据中t精确到秒,故ts以整数秒为颗粒度,相当于对实际秒数向下取整,误差<1 s。
ts从前车收费记入系统开始到后车收费记入系统为止,有以下特征:(1)ts包括前车缴费后拿取票据(仅MTC车道)、驶离收费亭、前后两次过车之间该收费亭空闲的无车时间、后车驶入收费亭以及收费前准备时间。(2)收费车道服务饱和时,视为连续服务前后两车。此时ts不包括无车时间,为实际单车服务时长。饱和期间所有过车ts之和为饱和期间时长。(3)饱和时单车服务时长将受前一车辆通行效率影响。
2 收费车道通行能力研究方法
定义收费车道通行能力为该车道在单位时间内所能服务的最大标准小汽车当量,并将通行能力估计问题转化为目标车道服务饱和期间通行各类车辆的平均服务时长分析问题。为此需优先明确:(1)目标车道允许通行车辆类型及其合并;(2)目标车道的通行能力饱和期间。
2.1 车辆类型合并
4个收费站ETC车道过车分为10种类型,以8月7日数据为例,过车占比统计如表1所示。
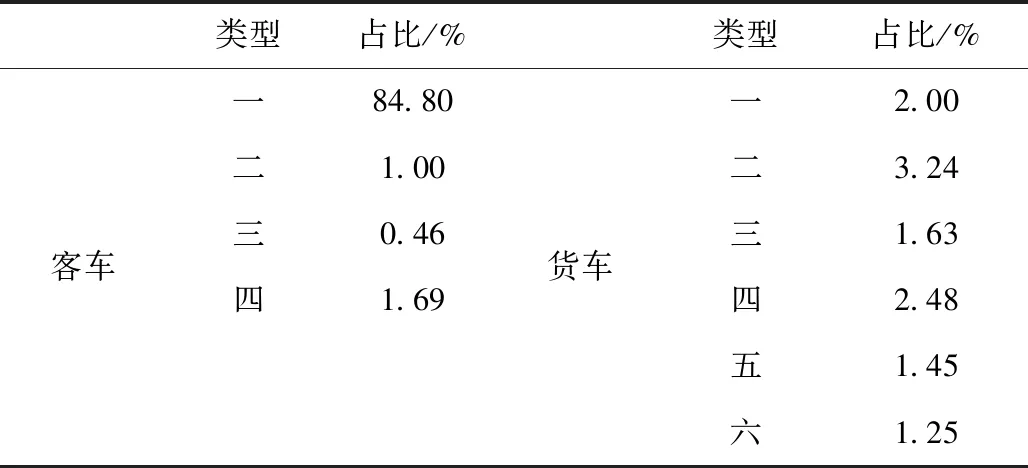
表1 8月7日4个收费站ETC车道过车类型占比Tab.1 Proportion of vehicle types on ETC lanes at 4 toll stations on August 7
车型分类过细将降低每类过车样本量而影响分析效果。按表1,一型客、货车数量之和占绝对优势,可单独分析;二型以上车辆综合占比不足15%,影响通行能力程度有限,可合并考虑。参考JTG B01—2014《公路工程技术标准》对代表车型的规定,合并一型客、货车为小型车,其余类型合并为大中型车分别研究。
MTC车道过车分ETC小、大中型车,MTC客、货车4种类型。8月7日4个收费站MTC车道过车组成见表2。其中ETC客、货运车辆综合占比小于10%,对整体服务时长分布影响有限,将其合并考虑。
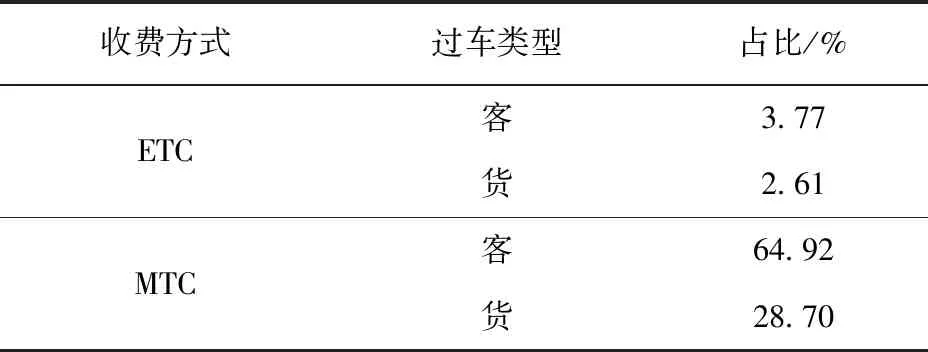
表2 8月7日4个收费站MTC车道过车类型占比Tab.2 Proportion of vehicle types on MTC lanes at 4 toll stations on August 7
2.2 通行能力饱和期间
各收费站区位及功能规划不同,其交通组成及车辆出行偏好存在差异,故确定车道通行能力饱和期间应针对不同收费站分别进行。
本研究选取的样本收费站为典型大流量收费站,有明确记录每日ETC和MTC车道均有拥堵发生,故数据样本中必定存在饱和期间,合理推断,每天最高流量时段中高强度服务车道处于饱和状态。但有研究[12]表明,收费车道的位置对其服务强度有明显影响,远离主线的车道即使在全站流量高峰时段也可能未达饱和状态,故取收费站流量高峰期间作为所有车道通行能力的饱和期间不可行。
本研究采用汇聚指定收费站同类车道所有数据的方法查找饱和期间,具体方法如下:对于同一收费站:(1)将其所有车道分别按15 min间隔集计分时流量;(2)将14 d内属于车道类型F的所有车道的15 min流量生成集合{V}F;(3)将{V}F按数值由小到大排序构成数列[V]F;(4)确定饱和期间占比,历史数据显示,样本收费站早晚高峰时长加和约为3.5 h,占全天时长15%,相应确定饱和期间对应15 min流量分位数Vl为85%分位数;(5)取{V}F中数值大于Vl的部分{VS}F,认为其中各元素所对应的车道在相应的15 min内处于服务饱和状态。此状态下对应的通行能力即为该站该类车道的通行能力代表值。
2.3 服务时长分布与通行能力计算
查找{VS}F中各时段包括的所有过车记录,提取每条记录的ts作为饱和期间单车服务时长样本,加入F模式下饱和期间单车服务时长集合{TS}F,进而研究饱和期间的服务时长分布。按已有成果[17-20],综合车道流量饱和期间各类过车的平均服务时长,可按式(2)求解指定收费站该类车道的饱和通行能力。
(2)
3 实例与分析
3.1 ETC车道服务时长
3.1.1 出口道
图1为8月3日3号收费站120#、130#ETC出口道所有过车间隔散点图,生成该站所有ETC出口道对应的饱和服务时长集合{Ts}e,分车道统计饱和服务时长热力图见图2,附不同车道流量和总体服务时长柱形图对比。
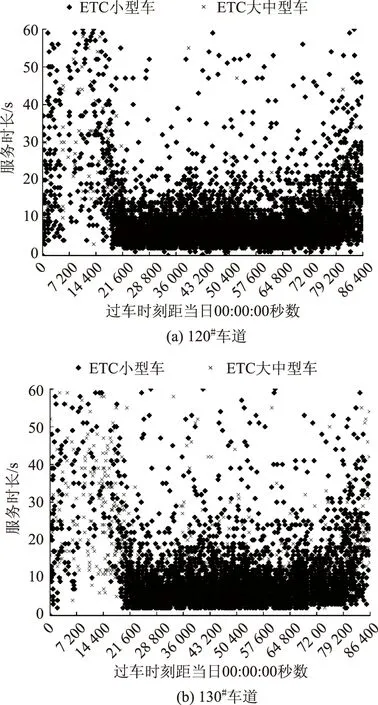
图1 3号收费站ETC出口道服务时长散点图Fig.1 Scattergrams of service time of ETC exit at toll station No. 3
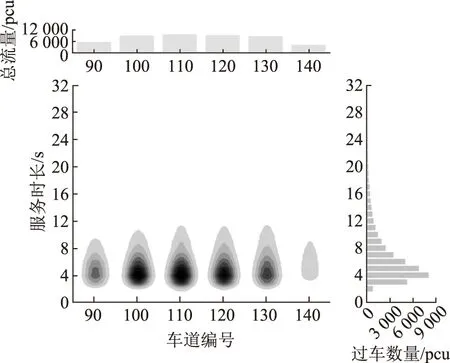
图2 3#收费站ETC出口道饱和服务时长热力图Fig.2 Heat maps of service time when ETC exit of toll station No. 3 is saturated
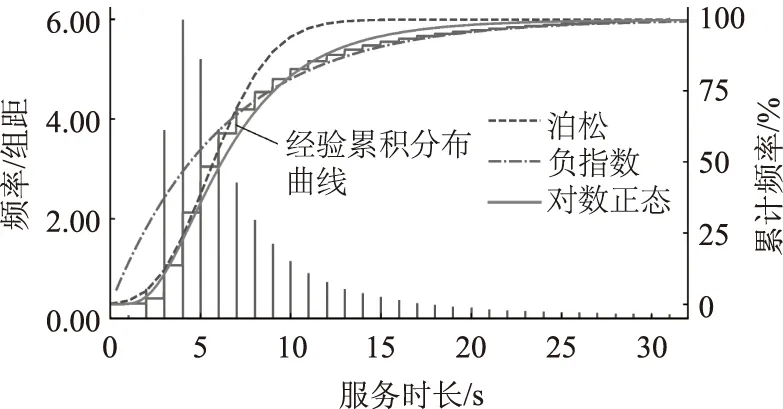
图3 3#收费站ETC出口道饱和服务时长分布Fig.3 Distribution of service time when ETC exit of toll station No. 3 is saturated
图3直观体现出μ′eE=0.16 s-1的负指数分布和λ′pE=6.37 s的泊松分布分别对服务时长较小、较大区间的分布形态描述能力较差。结合Q-Q图检验,μ′lE=6.38 s的对数正态分布全程拟合效果最好。进一步按小、大中型过车划分子数据集,拟合各自服务时长分布见图4,同样辅以Q-Q图检验,拟合参数为μlEs=6.11 s和μlEl=8.73 s的对数正态分布分别呈现了最优拟合效果。
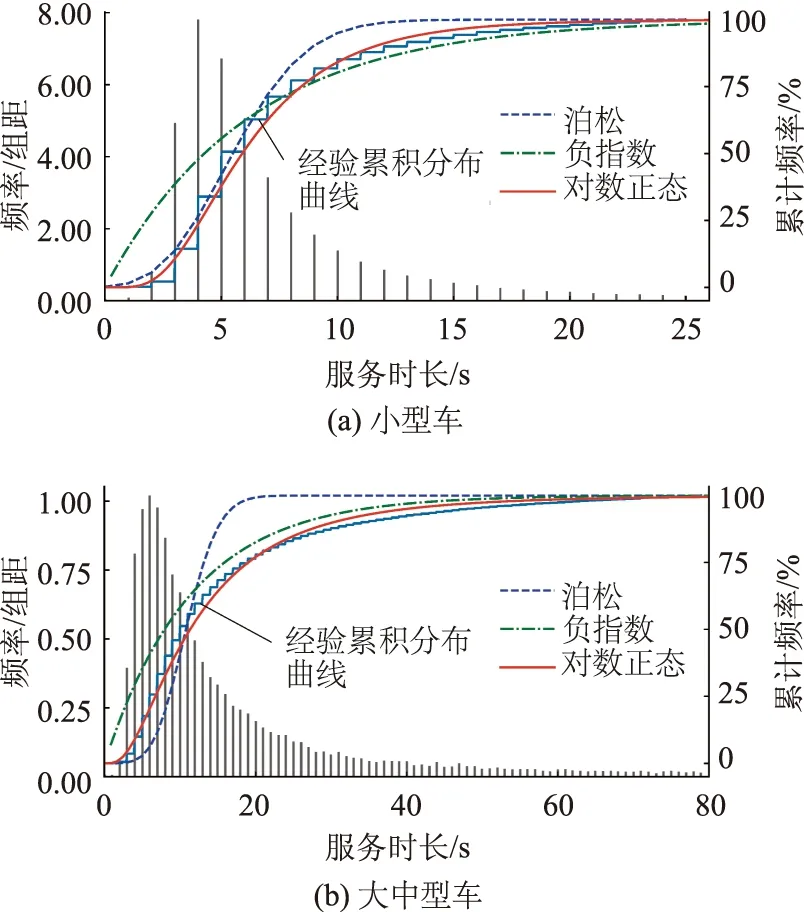
图4 3#收费站ETC车道不同过车类型服务时长分布Fig.4 Distribution of service time for different vehicle types in ETC lane of toll station No.3
基于排队论计算收费站通行能力多假设或基于少量数据拟合服务时长服从负指数分布或正态分布,进而以样本均值作为服务时长[22-23],但上述分析显示无论对于总体还是分类过车,对数正态分布拟合饱和服务时长效果均优于上述两种分布。
为观察过车占比影响及同一收费站在不同日期的饱和服务时长波动,将14 d数据按日期划分子集。2#,4#收费站14 d小型车占比在4个收费站中分别为最低和最高,有一定代表性。沿用前文标记符号,其部分计算结果如表3所示。
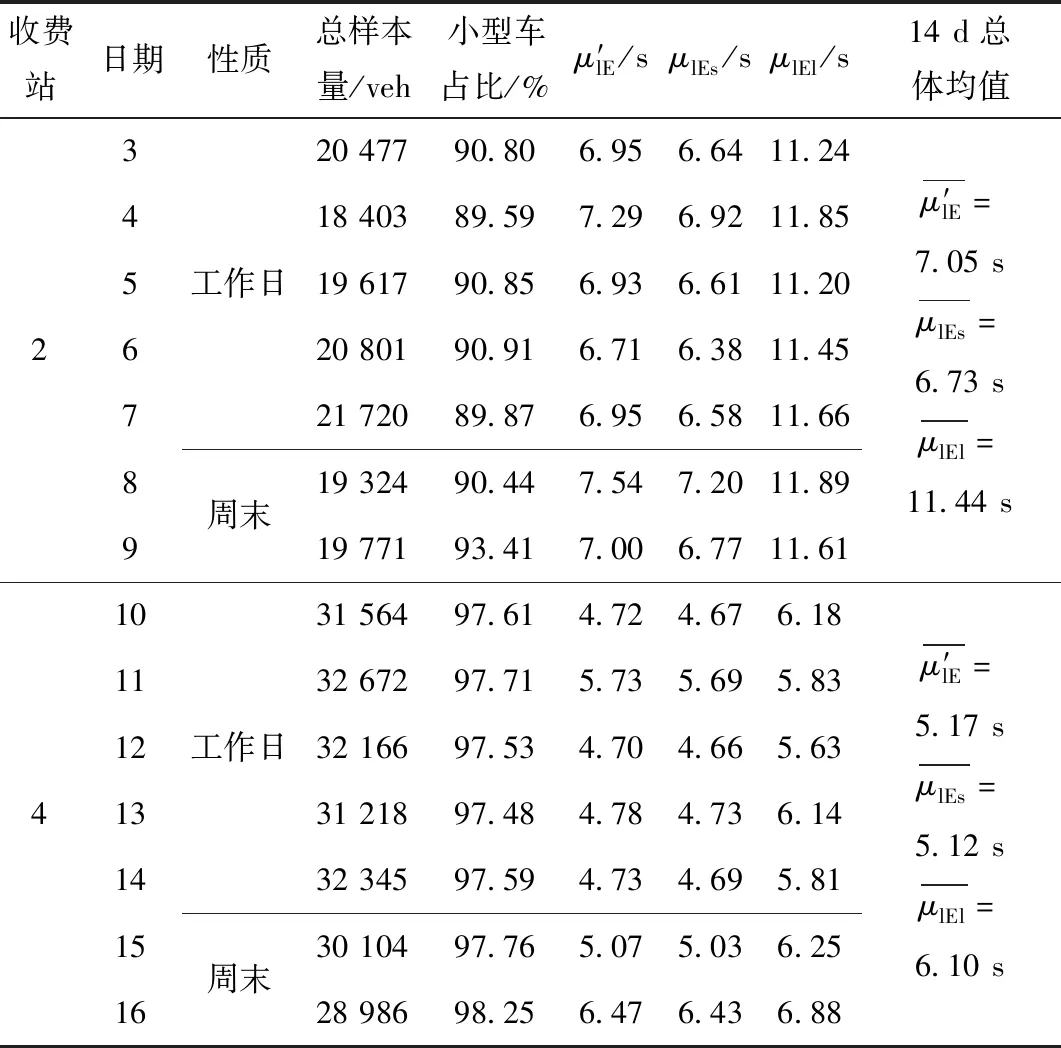
表3 2#、4#收费站ETC出口道饱和服务时长分布拟合参数Tab.3 Fitting parameters of distribution of service time when ETC exits of toll stations No. 2 and No. 4 are saturated
表3结果证明,比例占优的小型车对ETC出口道服务水平影响更大,体现为其饱和服务时长分布拟合均值更接近总体;虽然不同收费站出口过车组成存在差别导致拟合参数不同,但同一收费站ETC出口过车组成比较稳定,拟合参数水平也更接近;综合4个收费站结果,总体及分类型的饱和服务时长多日均值接近综合多日记录拟合均值,二者可相互替代。
3.1.2 入口道
同样研究ETC入口道服务时长,以大中型车辆占比最高的1#收费站和样本量最多的3#收费站为例,对数正态分布拟合效果仍然最佳,拟合参数结果见表4。数量占优的小型车仍对入口整体服务时长影响较大,而大中型车辆的影响随其占比增加也有一定体现,不同收费站ETC入口道的服务时长同样存在差异。
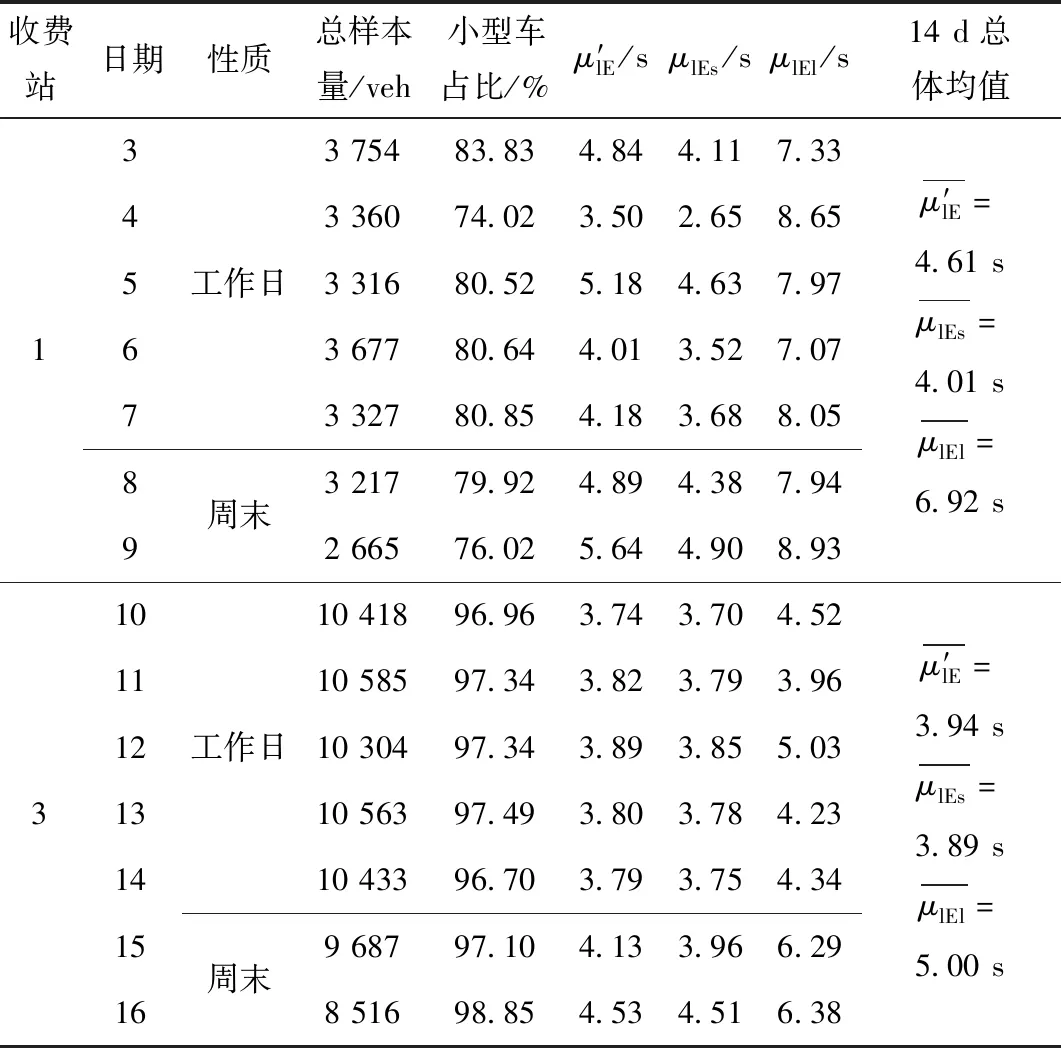
表4 不同日期1#、3#收费站ETC入口道服务时长对数正态分布拟合参数Tab.4 Fitting parameters of lognormal distribution of service time of ETC entrances at toll stations No. 1 and No. 3 on different dates
3.2 MTC车道服务时长
3.2.1 出口道
医院中央空调系统运行时,为了保证空调效果,门窗都要求关闭,如果新风量不足会造成室内空气污浊,不利于病人的康复和医疗工作者的身心健康。如何提高空调系统运行的舒适度,同时降低空调系统运行费用是暖通设计师需要考虑的问题。在民用空调系统中温湿度独立控制系统由于其显著的节能特性得到越来越广泛的使用,在医疗卫生系统的空调系统设计中,由于医院新风的重要性,对新风的处理不但要求达到相应的露点温度的要求,同时还要保证新风的洁净度和品质,防止新风污染,本文综合考虑几种新风除湿方式提出了双冷源新风机组在医院新风处理中的适用性,并通过运行数据分析了双冷源新风机组的节能特性。
图5为8月3日3#收费站160#、220#MTC出口道过车间隔时长散点图。与ETC出口道不同,各MTC车道的过车组成差别明显,间接影响了不同车道的服务水平。在数据条件理想情况下,应对各MTC车道单独分析。但由于MTC单根车道的日过车样本量较少,不利于保证服务时长分布拟合的可靠性,故仍以收费站所有MTC车道过车作为数据集整体分析,再进一步考察不同客货车流量比例对服务时长的影响。
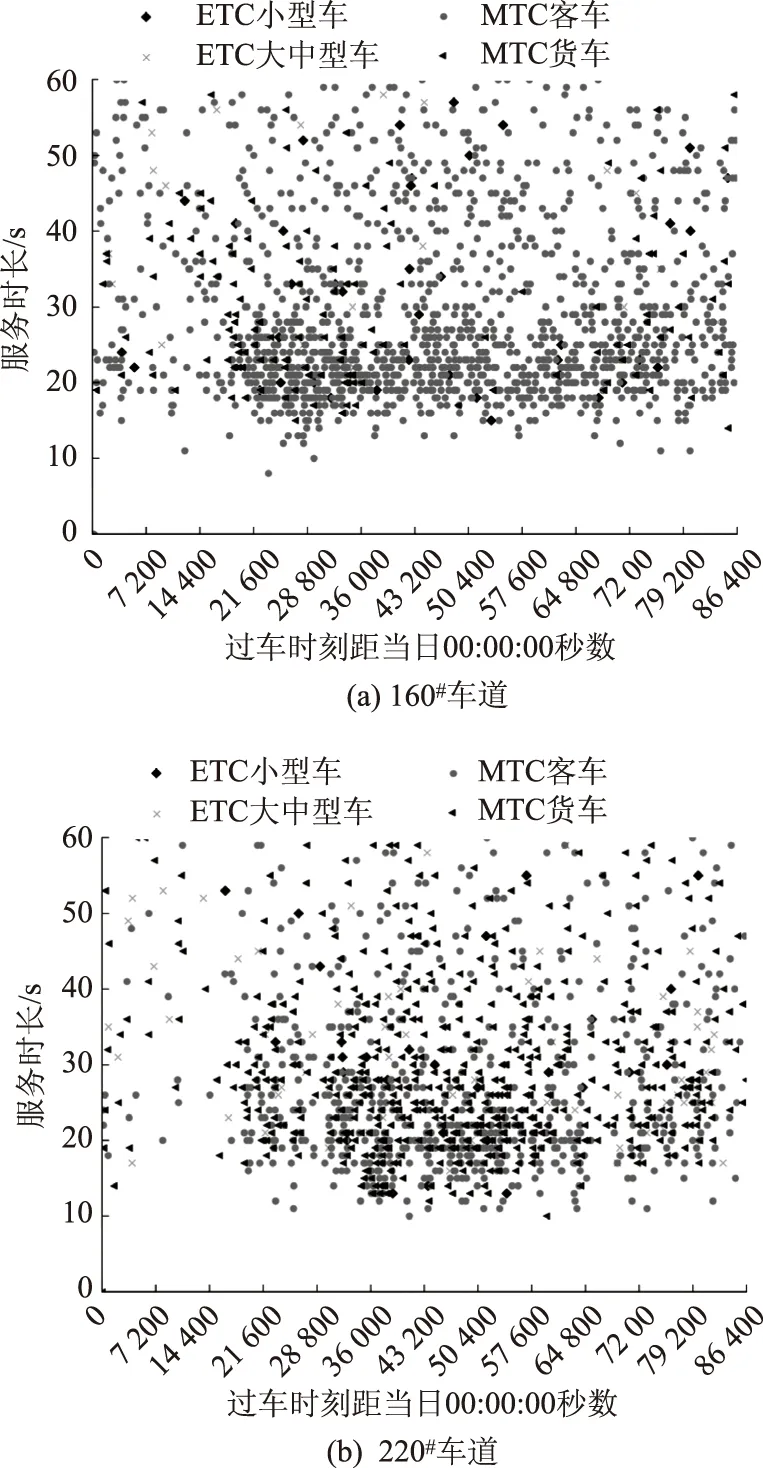
图5 3#收费站MTC出口道服务时长散点图Fig.5 Scattergrams of service time of MTC exit at toll station No. 3
分析3#收费站所有MTC出口道对应的饱和服务时长集合{TS}m,分车道绘制饱和服务时长分布热力图如图6所示,可见:(1)MTC出口道日流量与ETC车道相差一个数量级,单车服务时长明显更长;(2)经MTC车道通行的ETC车辆饱和服务时长分布相对ETC车道更离散、时长增加,在[15 s,35 s]区间集中,按照第1节对服务时长组成的解释,MTC车道的其他车辆严重影响了同车道ETC车辆的通行速度;(3)图6(a)显示,小型车和大中型车的服务时长分布呈现类似对数正态分布的趋势且峰值相近,可见将二者合并分析具有合理性;(4)在MTC车道通行的MTC车辆流量占优,饱和服务时长的对数正态分布趋势更明显,分布更集中;(5)两种收费方式的车道流量分布显示,ETC小型与大中型车辆、MTC客车与货车选择车道行为偏好不同,即使MTC车道的理论通行能力相同,驾驶员实际选择车道的偏好也会影响车道的使用效率。
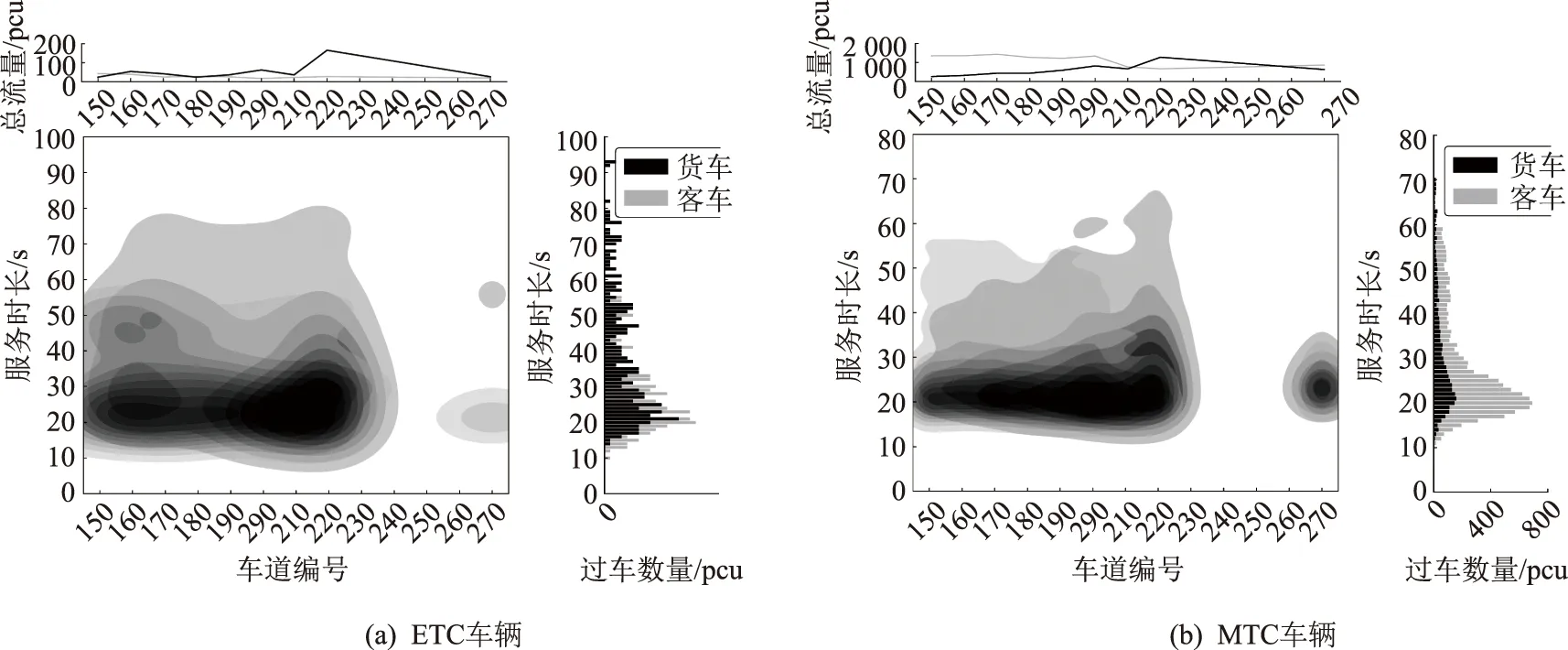
图6 3#收费站MTC出口道饱和服务时长热力图Fig.6 Heat maps of service time when MTC exit of toll station No. 3 is saturated
考察8月7日4#收费站所有MTC出口道的总体饱和服务时长分布见图7,由于较小服务时长区间累计频率增长更慢,以对数正态分布拟合MTC车道服务时长优势更明显。
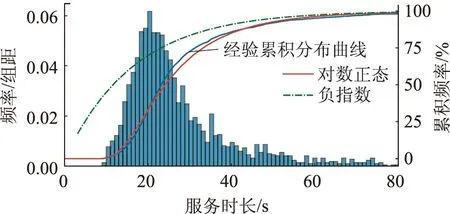
图7 4#收费站MTC出口道饱和期间服务时长分布Fig.7 Distribution of service time when MTC exit of toll station No. 4 is saturated
同样,按车型分割当日过车数据集,分别拟合服务时长结果见图8,Q-Q图同样说明了对数正态分布拟合的显著优势。
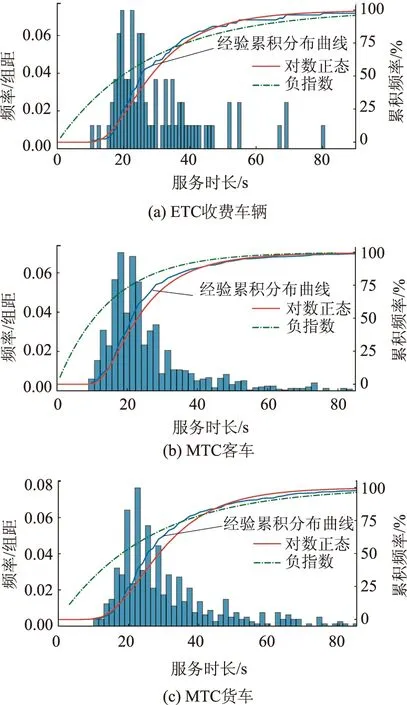
图8 4#收费站MTC车道不同过车类型服务时长分布Fig.8 Distribution of service time for different vehicle types in MTC lane of toll station No. 4
表5给出了部分日期3#,4#收费站MTC车道饱和服务时长的对数正态分布拟合结果。其中μ′lM,μlME,μlMc,μlMt分别代表通过该收费站MTC车道的所有过车、ETC收费车辆、MTC收费客车以及MTC收费货车的服务时长拟合参数。
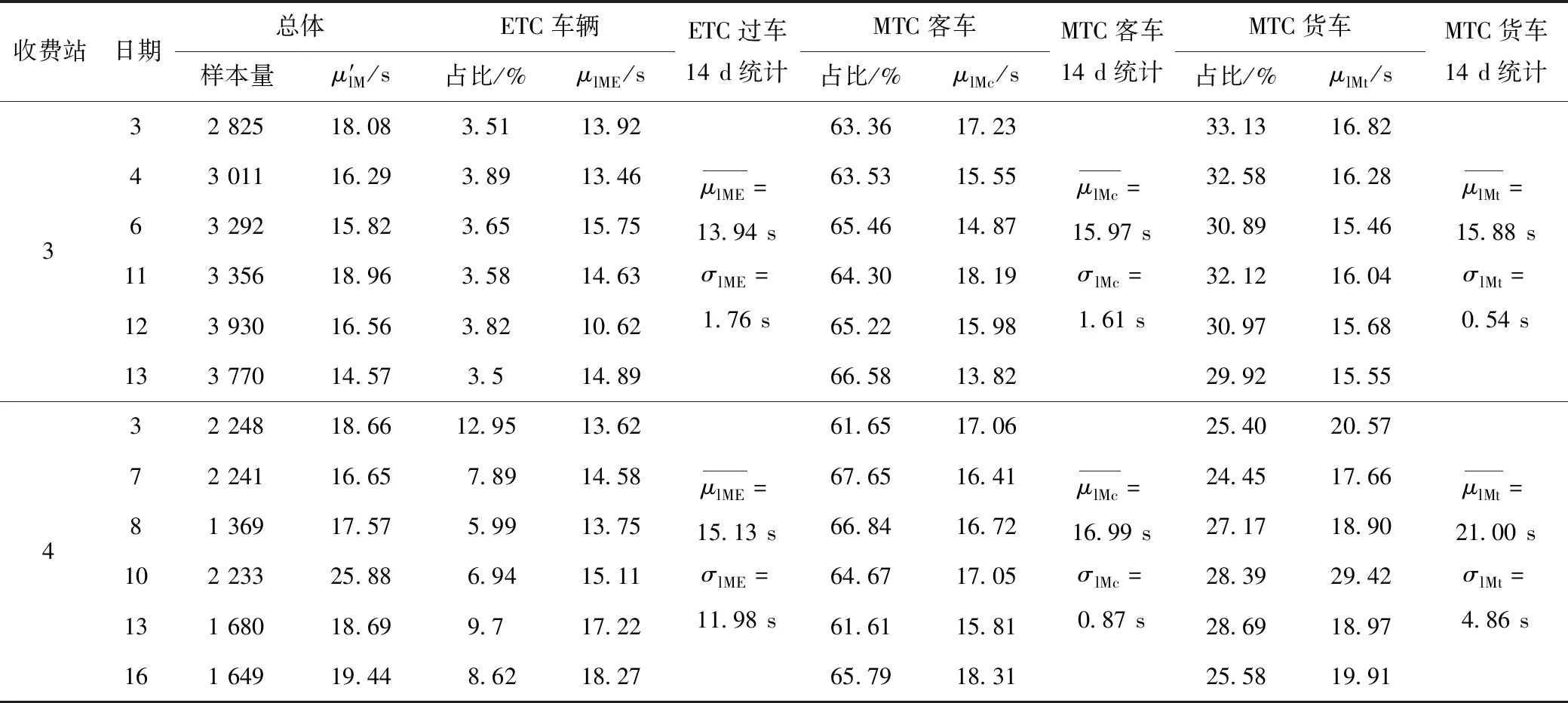
表5 不同日期3#,4#收费站MTC出口道服务时长对数正态分布拟合参数Tab.5 Fitting parameters of lognormal distributions for service durations of vehicles exited using MTC in Station 3 and 4
3#收费站过车类型占比相对稳定,ETC过车服务时长最小,MTC客、货服务时长水平接近;4#收费站过车组成不稳定,MTC客、货运服务水平差别明显,且不同日期货车服务时长分布拟合参数波动较大。特别地,综合14 d数据发现两个收费站总体服务时长拟合均值随MTC货车过车占比增加而增加,但程度不同,即使MTC货车占比更高,3#收费站各类车辆的服务水平明显高于4#收费站。这一发现再次证明了按收费站分别分析同类收费车道通行能力的必要性。
由于部分收费站MTC出口道的ETC过车数过少,无法拟合其服务时长分布。建议实际应用中对这类车道仅考虑MTC过车,将其服务时长集合作为单个车道的服务时长评估依据。
3.2.2 入口道
仍以对数正态分布拟合MTC入口道服务时长。3#,4#收费站MTC入口道ETC过车占比均小于0.5%,样本量无法支持分布拟合;但1#收费站ETC小、大中型车占比均超过20%,故分别拟合将参数记作μlMs和μlMl,部分结果如表6所示。不同收费站MTC入口服务时长分布明显不同:1#收费站MTC和ETC的各类车型通行速度水平相近;而3#收费站MTC无论客、货运,服务时长明显更高,且客、货运车辆也相差较大。可见,以往基于设计规范的统一建议值估计MTC车道通行能力的方法并不可靠。
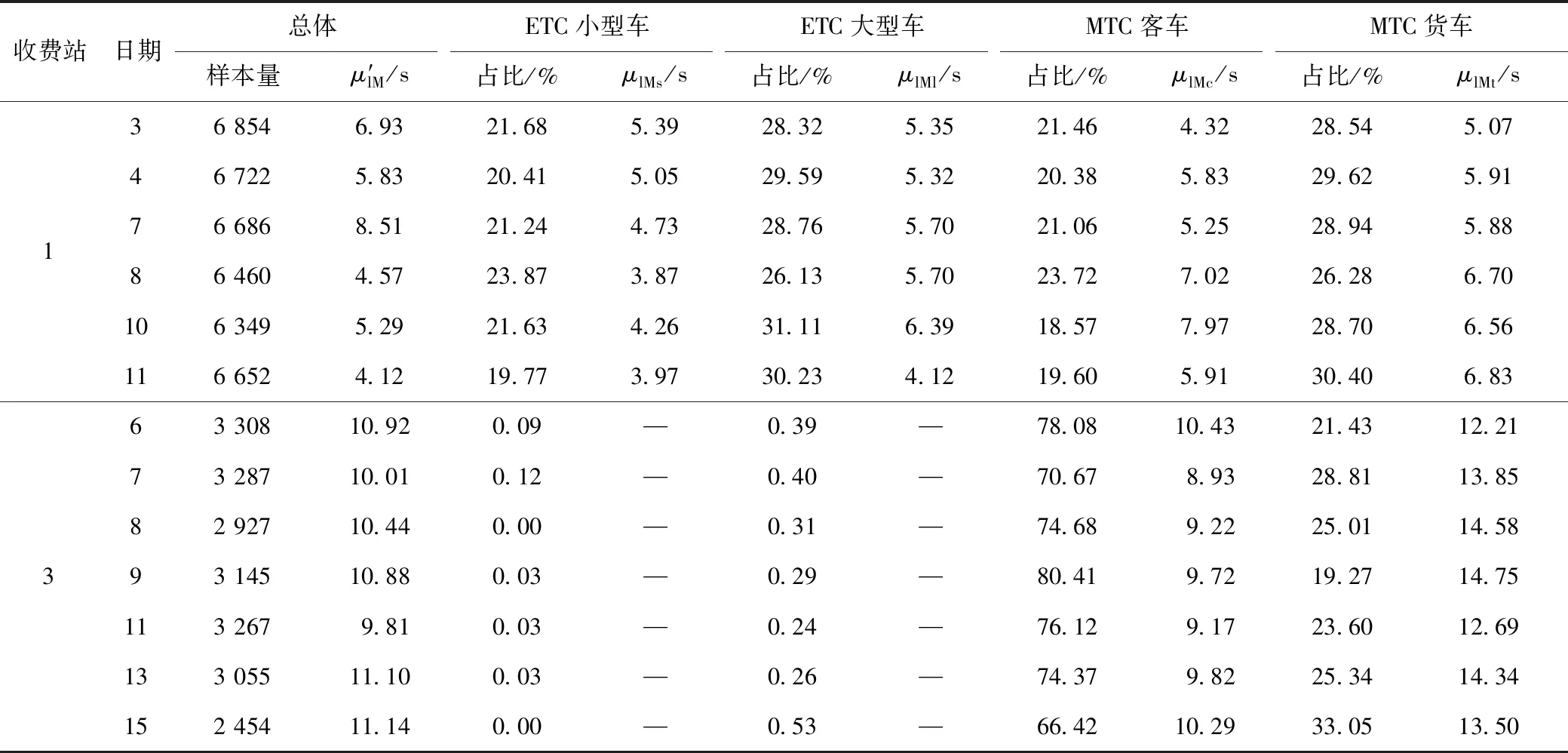
表6 不同日期1#,3#收费站MTC入口道服务时长对数正态分布拟合参数Tab.6 Fitting parameters of lognormal distribution of service time of MTC entrances at toll stations No.1 and No.3 on different dates
3.3 通行能力计算
按照式(2)分别计算1#~4#收费站各类车道平均通行能力如表7所示。可见不同收费站出、入口的ETC/MTC车道服务受收费站管理能力以及过车组成影响,呈显著不同的水平,故实际应用中应分别测算,而不应采用统一标准值。如需具体分析单根车道或指定时段的通行能力,可基于历史数据以对数正态分布拟合求解。
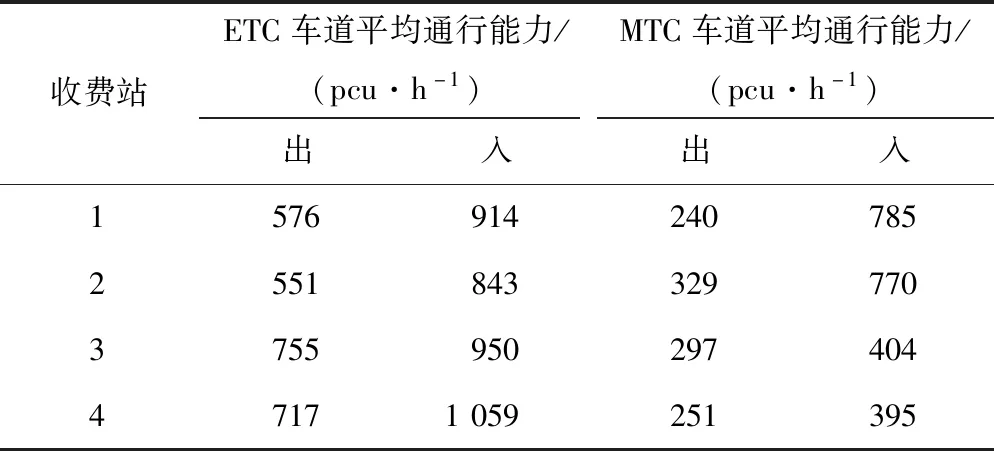
表7 1#~4#收费站不同类型收费车道平均通行能力Tab.7 Average capacity of different types of toll lanes at toll stations No. 1-4
以上代入式(2)求解该收费站各类车道通行能力时,Pc参数取值为同类多个车道的过车类型占比平均值。但如前文分析,实际上各车道过车组成存在差异,且对服务水平产生了显著影响。故应考虑其各车道的过车组成特点,在平均通行能力基础上微调得到最终的单车道通行能力结果。此外,在数据不足而必须参照类似车道或全站标准通行能力确定某根车道的通行能力时,也需充分考虑过车组成的影响。因此,研究描述随时间变化的车道过车组成描述方法很有必要。
3.4 车道过车组成描述方法
图9为1#收费站连续14 d 3根ETC出口道(编号90,80,20,按照与主线对应距离由小到大排序)通过小型、大中型车的流量变化图,按15 min间隔统计。
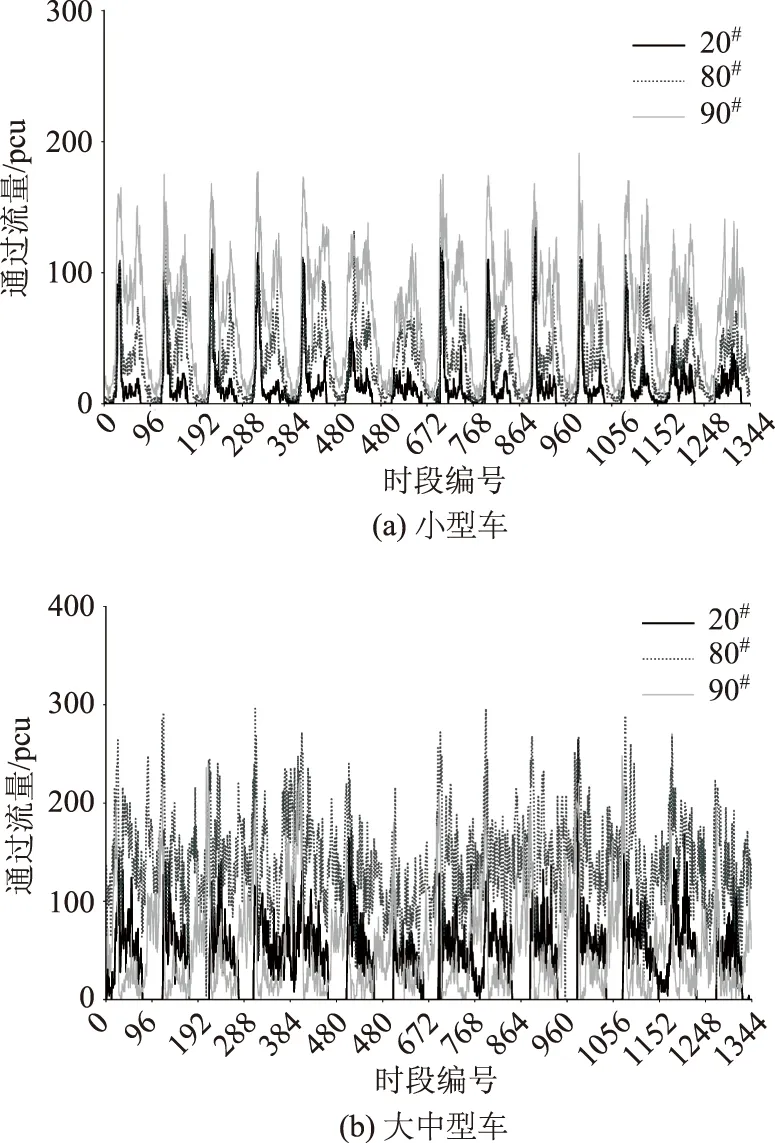
图9 1#收费站ETC出口道过车流量Fig.9 Traffic volumes of ETC exit in toll station No. 1
可见不同车道各类过车流量呈周期性变化,但不同过车类型在选择车道时有不同倾向。以最靠近主线的90#车道为例,与其他两个车道相比,该车道小型车流量始终占优而大中型车流量较少,且时间分布特征明显:午夜与凌晨大中型车数量较多,白天则小型车数量更多,两类过车流量呈相反变化趋势,如图10所示。
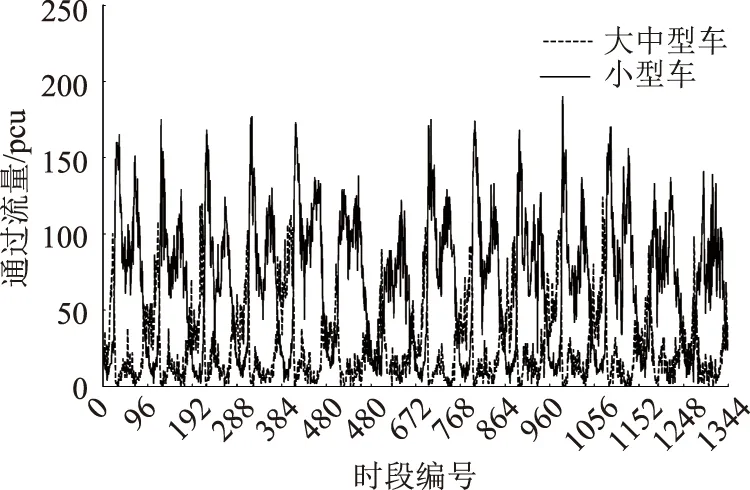
图10 示例车道不同过车类型流量变化趋势Fig.10 Change trend of traffic volumes of different vehicle types in example lane
为描述车道过车占比的变化,对如下3种方法进行考察:
(1)基于日占比曲线可复现性描述
以15 min间隔计算每日各类过车占比,对应每天各形成一个由96个元素构成的数列,以皮尔逊系数为指标,检查每两天占比曲线之间的相似性。以1#收费站90#车道小型车辆占比为例,其14 d日占比曲线相似性热力图如图11所示。结合其他收费站车道的观察结果,得出结论:日占比曲线可复现性不佳,不能用于描述车道过车占比。
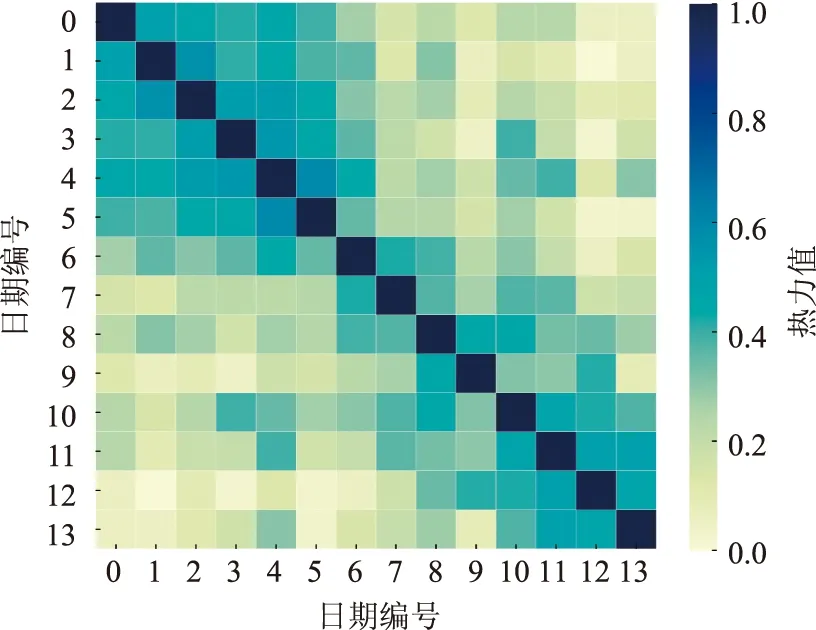
图11 示例车道小型车占比曲线相似性热力图Fig.11 Simiarity heat map of proportion curve of small cars in sample lane
(2)基于平稳时间序列的特性描述
将各类过车占比数列视为时间序列,观察其本身是否为随机数列,或是否可简单表示为周期性特征数列与随机数列的线性组合,又或其组成成分可表达为形式一致、参数稳定的自回归模型,则便于对其描述。
经过ADF检验,各收费车道过车的占比数列均为平稳数列,将1#收费站90#车道小型车占比数列做成分分解结果如图12所示。
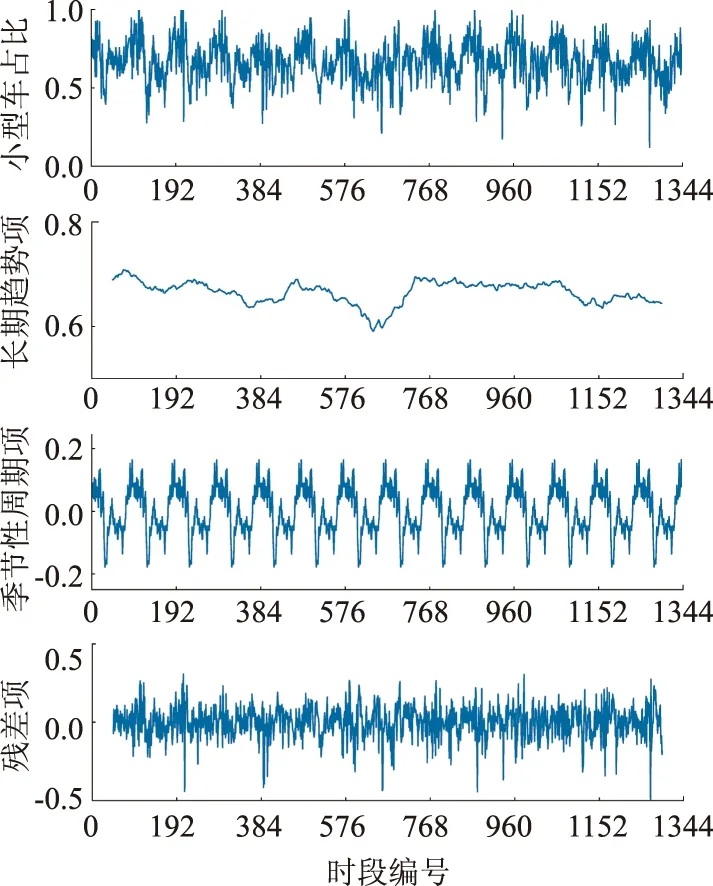
图12 示例车道小型车占比数列成分分解Fig.12 Decomposition of proportion sequence of small cars in sample lane
但分解后的残差项未通过Q检验,即残差项仍非白噪声序列。尝试对多个过车占比原始数列及残差数列分别进行ARMA建模,自回归项数与滑动平均项数均不一致,得出结论:无法以时间序列描述过车占比稳定规律。
(3)基于分布描述
以1#收费站3个车道各类过车占比数列为例,使用K-S检验其是否服从正态分布,发现正态分布对均值接近0.5的占比样本数列拟合效果较好,但由于占比限值在[0,1]区间内,均值偏离0.5,尤其当均值小于0.2或大于0.75时数列明显呈偏态分布,此时伽马分布拟合效果更好;而对于正态分布适用的场景,伽马分布拟合效果与正态分布偏差较小,如图13所示。对于其他收费站车道各类过车占比拟合结论一致。
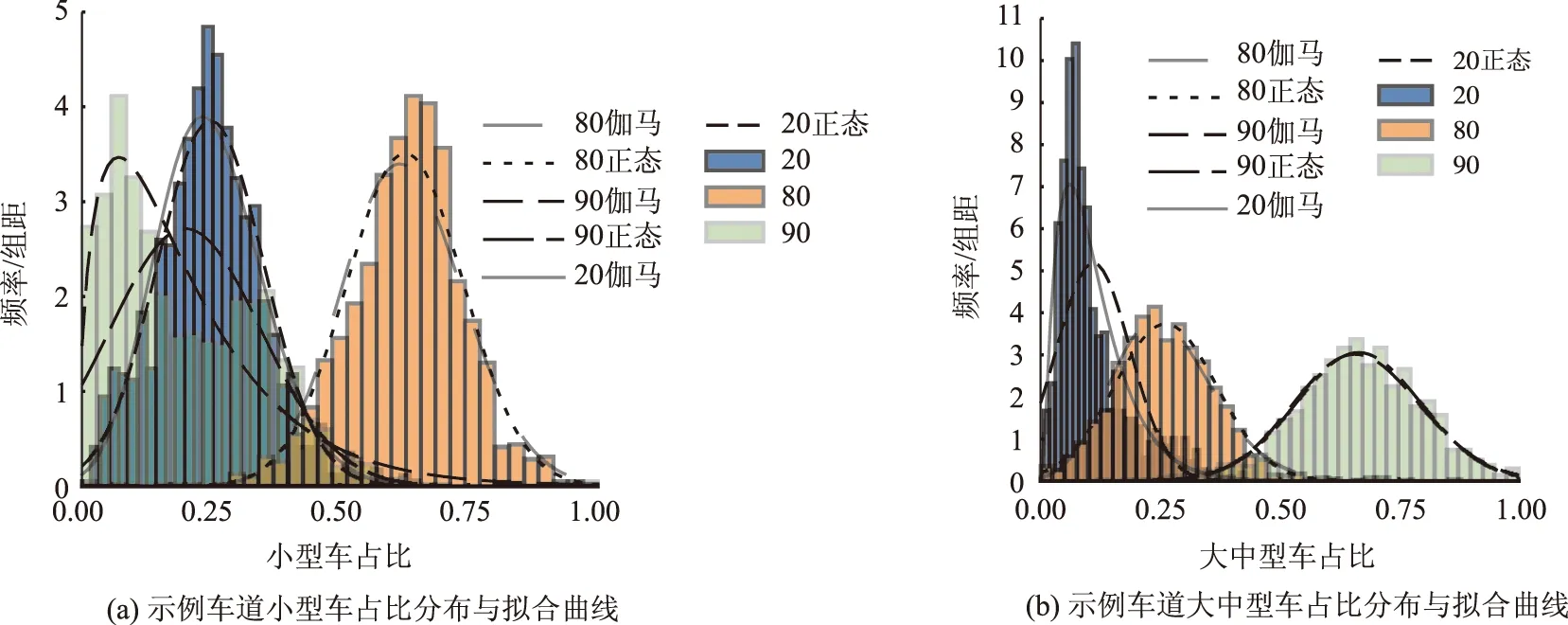
图13 示例车道各类车辆占比分布与拟合曲线Fig.13 Proportion distributions and fitting curves of different vehicle types in sample lane
综上,与曲线可复现性和时间序列方法相比,基于伽马分布描述车道过车占比的方法更可靠。结合前文分析,在数据条件良好时,可在线检测各车道过车类型占比变化以标定特定车道或动态调整车道的估计通行能力;在数据条件欠佳时,可基于历史数据以伽马分布拟合占比作为相对同收费站不同车道通行能力的调整依据。
4 结论
基于真实收费过车数据,通过服务时长研究不同类型车道的通行能力,有如下结论:
(1)分收费模式统计所有过车及按过车类型分割的饱和服务时长子集,对数正态分布拟合效果均优于正态分布和负指数分布;提供了可借鉴的ETC/MTC出、入口道通行能力数值。
(2)实际应用中套用统一的收费车道通行能力标准值并不可靠,应结合收费站区位及过车类型占比分别测算,或根据已有类似收费站的实测值确定;估算时对占比较小且服务特征相近的过车类型可合并分析。
(3)即使同收费站同类收费车道,因其与主线对应位置不同或特殊管制要求,对各类过车承担比例不同,导致通行能力存在差异,其中大型车或货车比例影响较大。不同车道过车类型占比的变化可用伽马分布描述,实际应用中可结合收费站总流量估计各车道过车组成,进而根据收费站同类车道平均通行能力调整对单个车道的通行能力估计,体现对其位置效用的考虑。
(4)未来将进一步扩充数据集,探讨过车类型占比与服务时长的相关性,研究具有普遍指导意义的车道级通行能力计算模型。

