基于迭代算法的PID控制器设计

何庭杰

摘要：针对传统的PID控制技术中参数优化难题以及就PID控制用于轨迹跟踪时存在收敛速度慢的问题， 提出了一种新的PID控制器设计方法。该方法首先构建基于输出反馈的PI控制器，然后把传统的PID参数求解问题转换为状态输出反馈K的求解，经数次迭代运算获得优化后的PID控制参数。仿真和实验结果表明， 采用该方法设计的PI-P控制器， 被控系统可以获得较高的控制精度和跟踪性能。

关键字：PID控制器;迭代算法;设计;仿真

1 PI控制器的设计

在控制输出点之后加入一个积分环节，给出基于输出反馈的PI控制器的表达式，考虑如下状态方程所描述的线性连续时不变随机系统为[1]：

由可控性判定定理可知，原系统S1-1是输出完全可控。因此，增广系统S1-3也是可控的。

2 输出反馈K的设计及指标约束控制研究

通过迭代算法，设计输出反馈K，使闭环系统S1-3既能满足单指标约束，又要满足多指标的约束。单指标约束包括极点指标、方差指标、指标;多指标约束有方差和幅值指标与衰减度指标相容、衰减度指标与指标相容。

2.1 极点指标

根据Lyapunov穩定性理论，由于闭环系统S1-3的极点配置在左半复平面的区域，必须使下式成立：

3 仿真和实验结果

为了验证该设计方法的有效性，本文以某火控随动系统的设计为例。在火控随动设计中广泛采用双环PI-P控制结构，将整个系统校正为Ⅱ型系统。Ⅱ型系统对于位置输入和速度输入都是无差随动系统，是种性能比较理想的随动系统。

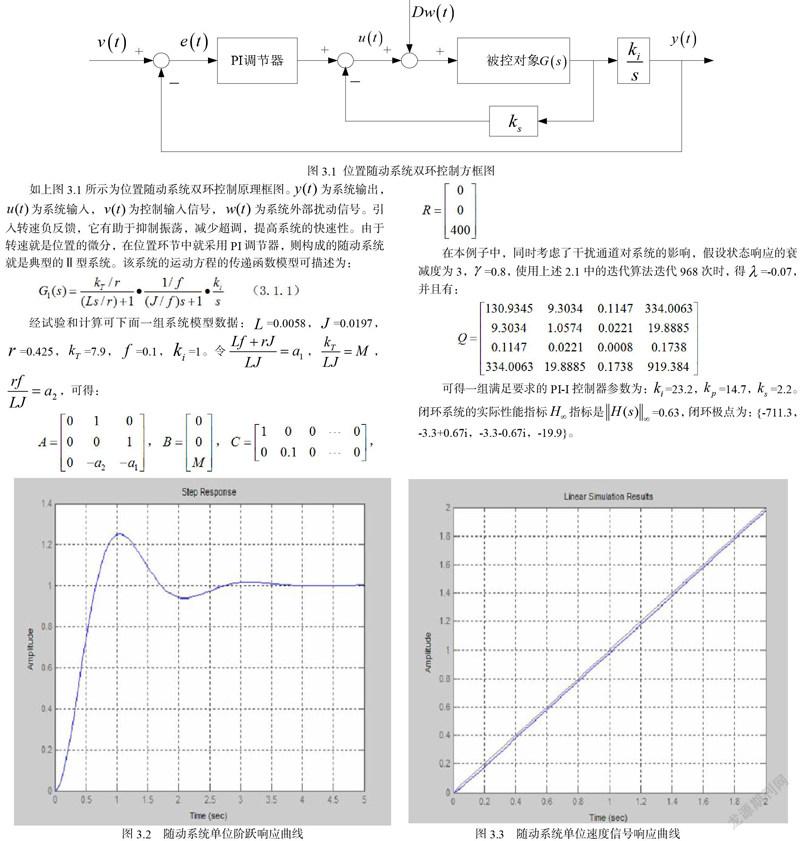
如上图3.1所示为位置随动系统双环控制原理框图。为系统输出，为系统输入，为控制输入信号，为系统外部扰动信号。引入转速负反馈，它有助于抑制振荡，减少超调，提高系统的快速性。由于转速就是位置的微分，在位置环节中就采用PI调节器，则构成的随动系统就是典型的Ⅱ型系统。该系统的运动方程的传递函数模型可描述为：

将所得的控制器参数代入如图3.1所示的系统进行MATLAB仿真试验。可得如图3.2为单位阶跃输入信号也就是位置输入时闭环系统的响应曲线，图3.3为速度为1时闭环系统的响应曲线，它表明系统的速度跟踪性能。其中虚线为给定的速度值，实线为系统实际速度输出值。结果显示该控制器的设计采用满意鲁棒控制的方法，有较高的控制精度和跟踪性能。

4 结论

PID控制器广泛应用于工业控制系统中，传统的PID调节方法过于复杂，且很难达到期望的动态响应。本文中提出了一种新的PID参数整定方法，利用基于迭代算法的LMI计算输出反馈来对系统参数进行整定。仿真和实验结果都证明了该方法的有效性，并且设计的PI-P控制系统，具有较佳的控制精度和较强的跟踪性能，完全可以应用到其它工业控制系统PID控制器的设计。

参考文献

[1]张怀相，原魁，邹伟.基于迭代学习控制的PID控制器设计[J].系统工程与电子技术，2006，28（8）：1225-1228.