基于粗糙遗传算法在打捆机齿轮箱故障诊断中的应用*
任彬,白东,谢虎,韩柏和,肖苏伟
(1.石家庄铁道大学机械工程学院,石家庄市,050043;2.农业农村部南京农业机械化研究所,南京市,210014;3.中国热带农业科学院橡胶研究所,海口市,571101)
0 引言
自走式连续作业打捆机作为一款新型的自动化、智能化农业机械产品,其关键部件齿轮箱长期处于高速、高载荷工作状态下,易出现疲劳磨损、胶合、断齿等机械故障。齿轮箱机械故障的发生会严重影响打捆机的正常作业,甚至延误农时,造成经济损失[1]。为了实现对不同故障类型的预测和防控,对齿轮箱实现故障诊断具有重要意义。
通过对振动信号时频域分析提取故障特征参量,将特征参量作为评价指标进而实现故障诊断识别是一种常用的故障诊断方法[2-10]。其中Hou等[11]利用稀疏编码和全局优化实现了滚动轴承弱故障特征的提取并进行故障诊断试验,诊断率达到100%;Zappalá等[12]提出采用边带功率因数作为评价齿轮状态的标准,有效的实现了故障自动诊断。但由于打捆机本身工作环境恶劣,振动信号成分复杂,同时常用故障特征参量冗杂,进一步提高了决策难度。因此,需要从众多的故障特征参量中提取出对故障诊断决策有意义参量集合,并使得该集合尽可能小,以保证决策过程的便易性[13]。
粗糙集属性约简理论是波兰学者Pawlak[14]提出的一种属性约简理论,娄玉华[15]利用粗糙集理论对提升机复合故障诊断决策表进行约简获得决策规则,通过试验证明该规则集能有效诊断提升机故障;刘慧玲等[16]结合粗糙集和神经网络,通过差别矩阵实现属性约简并利用神经网络实现诊断,试验结果表明该方法能有效实现故障诊断并提高诊断效率。经典粗糙集属性约简主要采用求核集的方式进行约简[17-20],由于属性约简属于NP问题,算法在决策表数据量大、属性集较多时效率低下。
综上所述,针对打捆机齿轮箱故障参量选取困难问题,采用粗糙集作为约简理论,并通过自适应遗传算法提高属性约简效率,得到最简故障特征参量集和决策规则表,并根据决策规则表实现故障诊断,本文利用打捆机齿轮箱振动信号对该方法进行试验验证分析。
1 粗糙遗传算法基本理论
属性约简是指在保持分类能力不变的情况下实现对冗余信息的剔除,即利用尽可能少的条件属性实现对决策属性的判断。当前属性约简主要利用粗糙集理论实现数据信息的约简,通过建立决策系统,利用不可分辨关系和正域等概念,遍历式的对不同的属性进行判断分析,剔除其中的非必要属性[21-24]。传统约简算法效率低,对先验信息依赖性大,遗传算法[25-26]作为一种启发式智能算法能有效提高约简效率,且无需先验信息。利用遗传算法实现属性约简,将决策属性对条件属性的依赖度作为遗传算法的适应度函数,将条件属性的不同组合作为遗传种群,通过选择交叉变异求得对决策属性最重要的条件属性,即最简属性集。
1.1 初始决策表建立
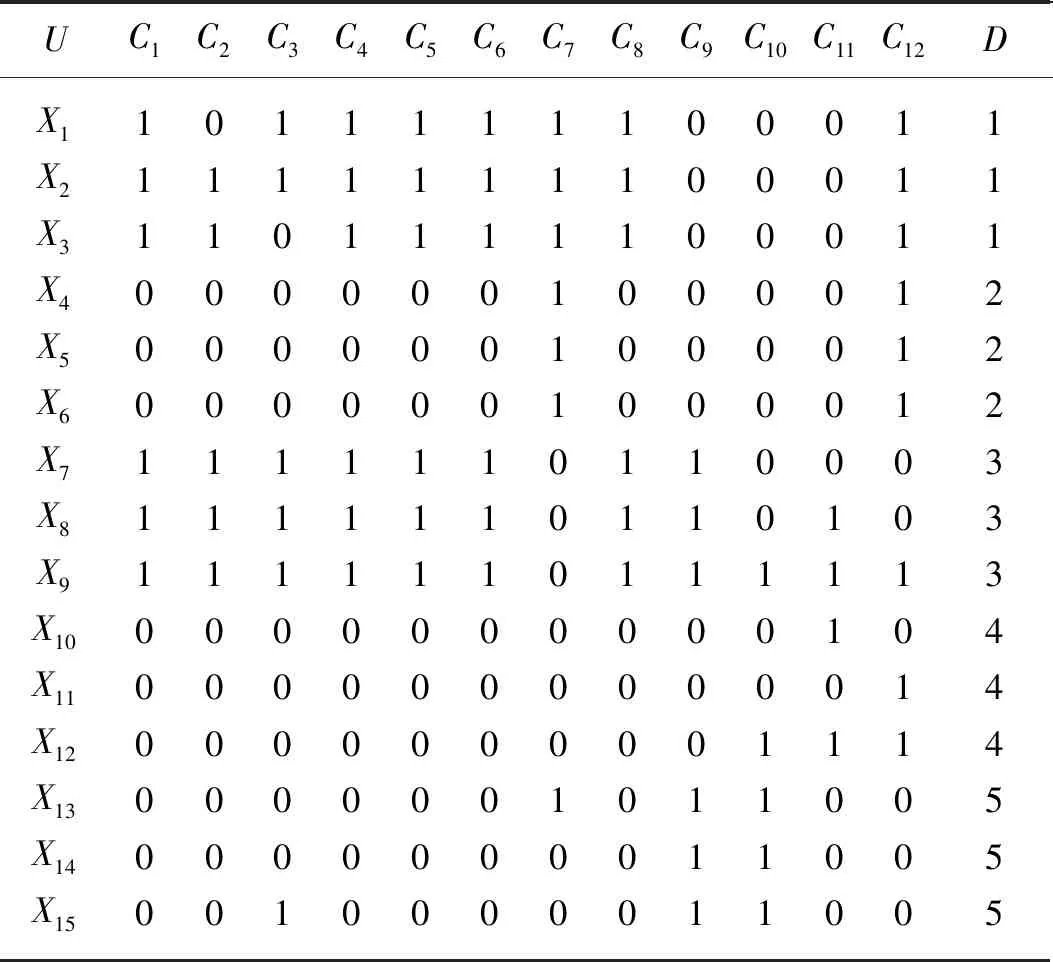
在利用属性约简实现故障特征参量的选取过程中,首先需要针对不同故障实例提取故障特征参量,并利用故障特征值建立初始决策表,决策表形式如表1所示。表1中U为论域,X1,X2…Xm为论域中的实例,Ci(Xj)为实例Xj的条件属性Ci的值,D(Xj)为实例Xj的决策属性值。

表1 决策表Tab.1 Table of decision
粗糙集理论只能处理离散的数据集,齿轮箱故障特征参数均为连续的数据值,因此需要对数据集实现离散化处理。为保证在决策属性分类能力不变的条件下使断点尽可能少,本文为采用SNS(Semi Naive Scaler)算法实现属性集的离散化[27]。SNS算法是NS算法的改进,是对NS算法求得的断点进一步删减,去除冗余的过程。
NS算法首先选取连续属性C,论域U中X的属性C值为C(X),U中实例按C(X)的大小进行排列。从上到下扫描全域,寻找断点。若存在条件C(Xi)≠C(Xi+1),且D(Xi)≠D(Xi+1),则认为该处存在断点pi=[C(Xi)+C(Xi+1)]/2。
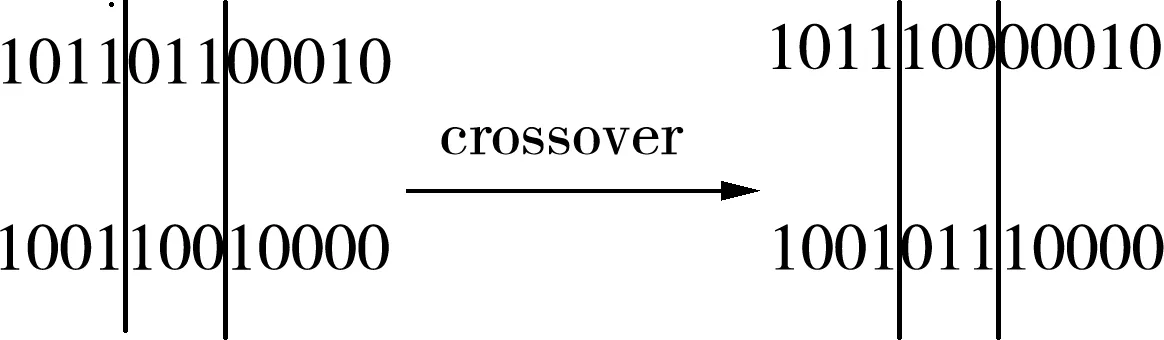
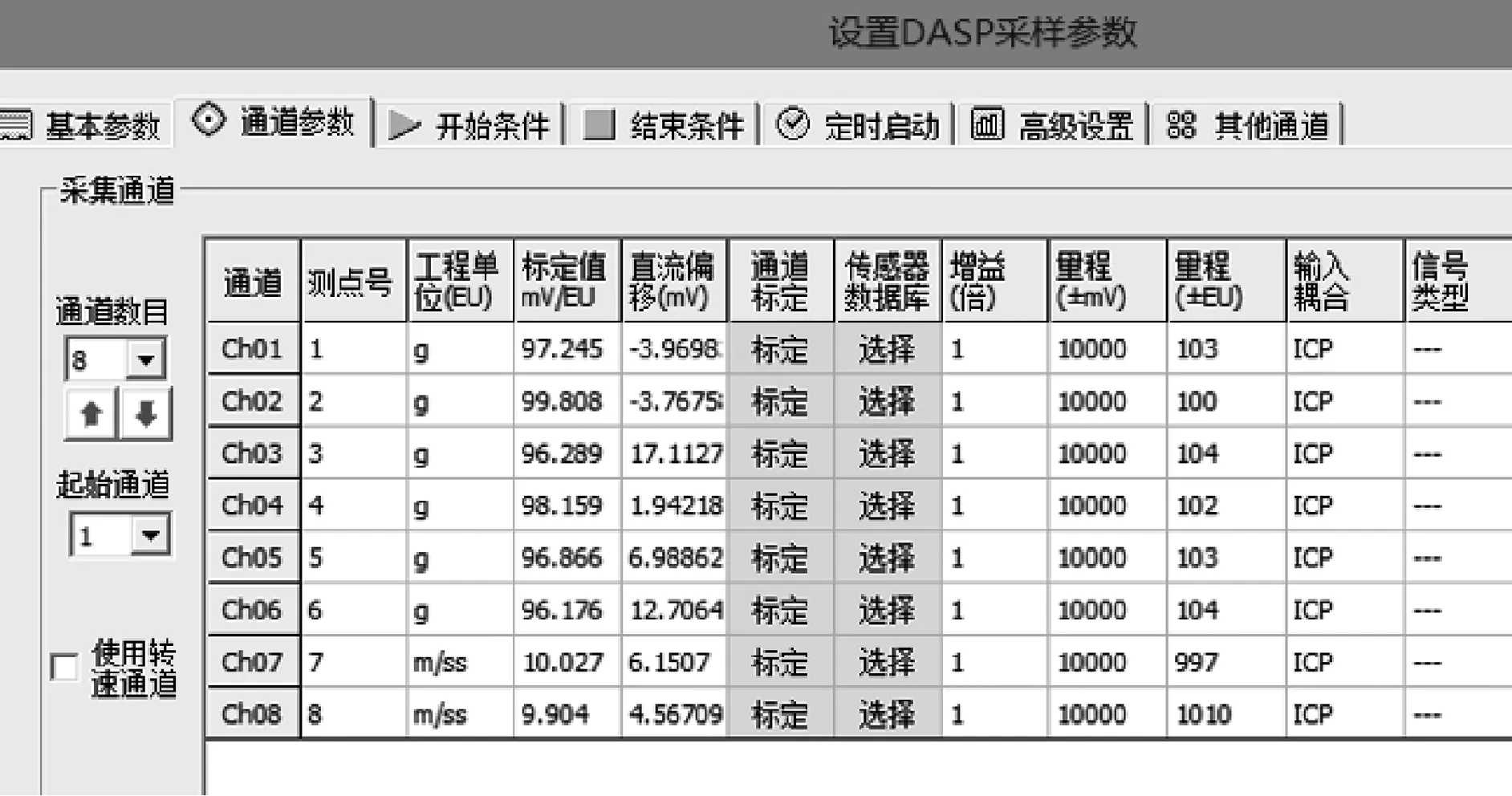
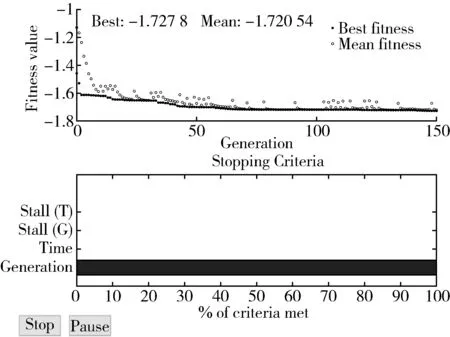
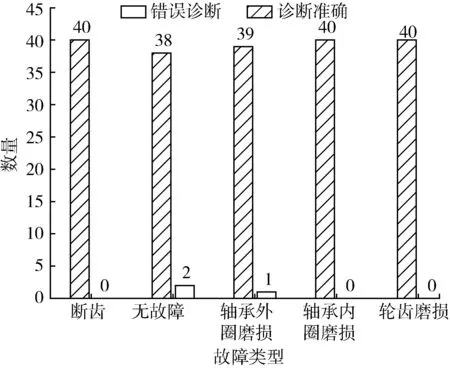
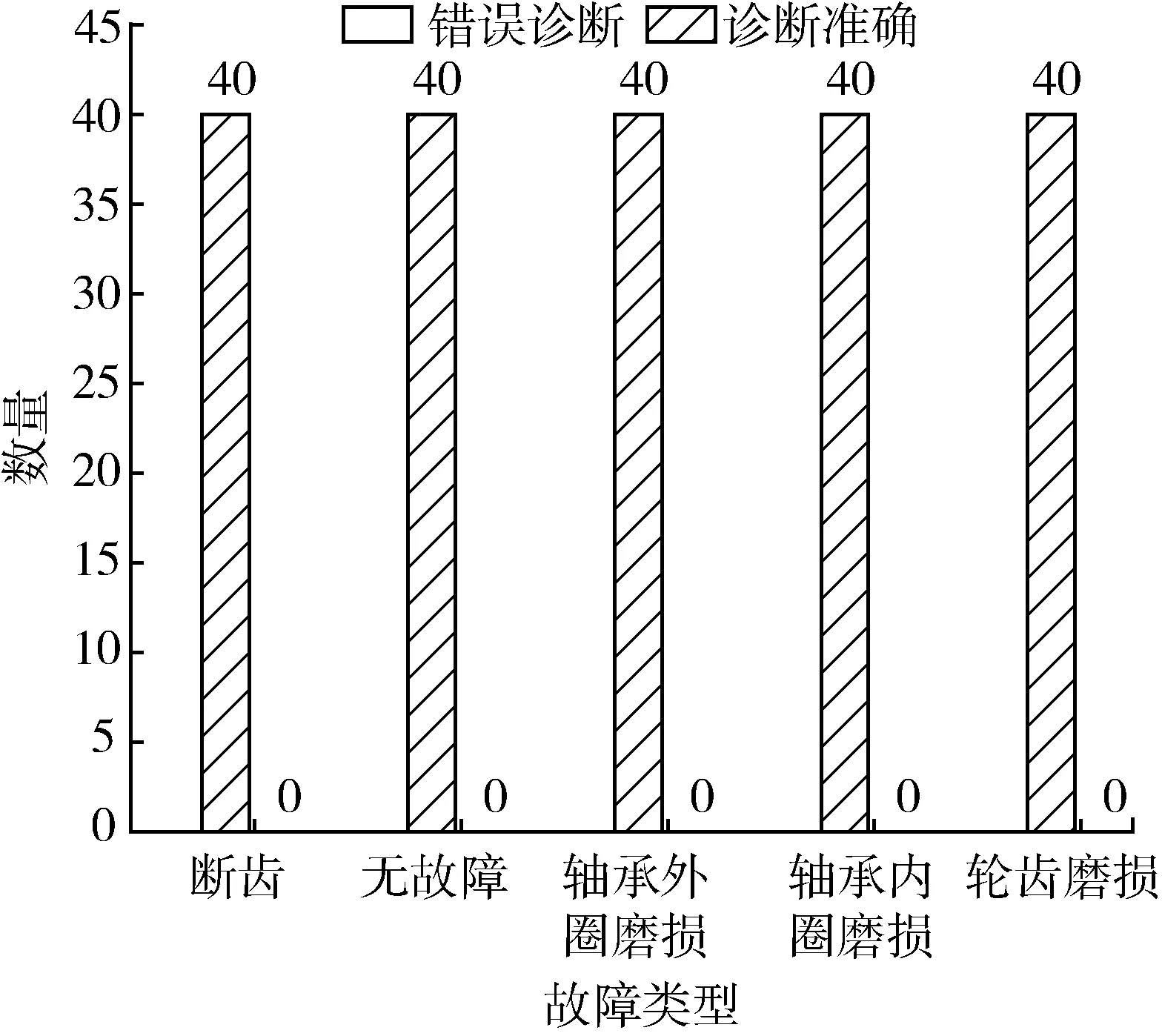
NS算法仅考虑单个的连续属性,因此断点较多,存在大量冗余。SNS算法针对NS算法得到的断点分别进行讨论,减少断点数量。针对决策表中属性C的某一断点pi,首先将U中实例按C(X)的大小进行排列,存在i使得C(Xi) 图1 SNS断点法流程图Fig.1 SNS breakpoint method flowchart 完成初始决策表的建立后,利用自适应遗传算法对决策表进行属性约简,算法流程如图2所示。 图2 遗传算法Fig.2 Genetic algorithm 基于自适应遗传算法的属性约简具体过程如下。 Step1:初始化种群。首先由算法随机生成多个染色体长度为L的二进制个体,个体的L条染色体分别代表初始决策表中的L个属性。若某染色体编码为1,则该染色体对应的属性保留,否则去除该属性。对于条件属性为C={C1,C2,C3…C12}的决策系统,随机生成某一个个体{110000100110}代表由C1、C2、C7、C10、C11组成的属性集个体。 Step2:设置适应度函数。适应度函数是评价种群中个体优劣的关键,在利用遗传算法实现属性约简的过程中,要求决策属性对约简后的条件属性集依赖度最大,同时保证约简后条件属性集最小。设适应度函数 (1) (2) 式中:L——染色体长度; Lr——染色体中各非零数数量值,约简后的属性集中包含的属性越多,则Lr的值越大,适应度F越低; γC(D)——决策属性D对条件属性C的依赖度,即条件属性集的重要程度[28]; POSC(D)——D的C正域。 Step3:设置迭代终止条件。(1)达到设定的最大迭代次数。(2)迭代过程中每次适应度提高低于设定阈值。若遗传算法满足以上终止条件,则输出当前种群中适应度最高的个体作为最优解。 Step4:选择、交叉和变异。对种群个体的选择采用轮盘赌博的方式,首先根据适应度的大小设定各个体的被选择概率,使适应度函数值较大的个体被选中概率更大,然后根据轮盘赌博的方式在初始种群中选取交叉、变异的候选个体。 交叉算子是算法的核心部分,如图3(a)所示。对种群中的个体成对随机匹配,匹配到的父代个体随机选择一个交叉区域,交叉区域长度不能大于等于染色体长度L。被选区域以交叉概率pc进行交叉变换。 (a)交叉示意图 变异是对种群中的个体染色体进行取反操作,对于候选变异个体,按照均匀分布随机产生变异点,按变异概率pm对该染色体进行取反操作,如图3(b)所示。 遗传算法中交叉和变异概率pc和pm对算法寻优结果有着较大影响,标准遗传算法采用静态的pc和pm值。根据算法原理可知,若pc值太大,算法会较快产生新个体,但适应度较高的个体会被破坏,该值太小会导致进化速度太慢;pm值太大,算法收敛速度会变慢,该值太小会使新个体减少,降低种群多样性[29]。基于该问题,Cao等[30]提出一种自适应遗传算法,该算法根据每个个体的适应度值大小,对pc和pm的取值给出了相关计算公式。 (3) (4) 式中:Fmax——种群最大适应度值; Favg——种群平均适应度; F′——发生交叉的两个体中适应度值较高的值; F″——发生变异的个体的适应度值; C1、C2、C3、C4——大于0小于1的参数。 Step 5:通过选择、交叉和变异产生新的子代种群,根据最优保存策略[31],取父代种群中的最优个体直接复制到子代种群,代替子代中适应度最低的个体,同时保证种群大小不变。 Step 6:对新的子代种群重复步骤4和步骤5,直到种群满足迭代终止条件。 遗传算法的每一次迭代都使得种群向着适应度更高的方向演变,经过数次的迭代后便可以得到优良的后代种群。通过遗传算法求得条件属性中对决策属性最重要的最简属性集,根据式(1)可知,该集合即对故障最敏感的最小故障特征参量集。 本文所选试验对象为研发的自走式稻麦秸秆收割打捆机样机,如图4所示。主要针对其齿轮箱的振动信号进行采集工作,在本次采集工作中自走式打捆机处于空载状态,分别采集3个不同转速区间的振动信号。现场试验分别采集了齿轮箱断齿、齿轮磨损、正常齿轮、轴承内圈及外圈磨损的故障信号。信号采集硬件设备选用INV982X加速度传感器和INV3810CT型采集仪,软件为DASP信号采集和实时分析系统。图5为打捆机齿轮箱上加速度传感器的布置位置,传感器通过采集仪进行驱动,并由采集仪存储采集信号输送给上位机,采集仪通过上位机的DASP软件进行设置,设置界面如图6所示。 图4 自走式稻麦秸秆切割打捆机样机Fig.4 Prototype of self-propelled straw baler 图5 打捆机齿轮箱振动信号采集Fig.5 Acquisition of vibration signals for gearbox 图6 DASP采集仪设置界面Fig.6 DASP collector setting interface 完成数据的采集和整理后,选取同一工作状态下的不同故障类型振动信号作为被诊断信号,并分别选取多组信号进行故障特征参量值的提取。对不同故障类型信号各取50组提取特征参量,选其中3组作为约简数据,40组作为测试数据。时域特征分别选取均值、最大值、峰值、有效值、均方根值、方根幅值、歪度、峭度、裕度及峭度指标,频域特征参量选取功率重心及功率谱分散程度。 完成故障特征参量的计算,将各组振动信号的故障特征参量作为初始决策表的条件属性C1~C12,齿轮箱故障状态作为决策属性D,其中数字1代表断齿故障,2代表正常齿轮,3代表轴承外圈磨损故障,4代表内圈磨损,5代表齿轮磨损故障。为了便于约简处理,采用SNS算法对初始决策表进行离散化,得到离散决策表如表2所示。 表2 离散后的故障特征决策表Tab.2 Decision table of fault feature is discrete 完成决策表的离散后,利用遗传算法对条件属性中的冗余属性进行约简。首先初始化遗传种群,并设置适应度函数式(1),并设置算法迭代的终止条件为:(1)达到最大迭代次数,本文设置最大迭代次数为150次;(2)迭代过程中连续15次迭代中适应度提高为0。 完成种群的建立和适应度的设置后,采用轮盘赌博的方式随机选取个体,进行交叉和变异,进而产生新的个体。对新产生的个体分别计算适应度值,并依据最优保存策略将其中适应度高的个体复制给下一代,算法迭代过程如图7所示。算法中遗传算法向目标值最小方向寻优,因此适应度函数设为负值。从图7可以看出,最佳适应度值以及平均适应度值在迭代中不断提高。 图7 遗传算法迭代过程Fig.7 Iterative process of genetic algorithm 遗传算法经过数次的迭代,得到最优解为{000001101000},则最简决策属性集为{C6,C7,C9}。表2中条件属性C1~C12经过约简仅保留{C6,C7,C9}3项属性,并对表中3项属性及决策属性完全相同的实例进行剔除,得到决策规则表,作为故障诊断知识库,如表3所示。 根据决策表3,故障特征参量由12项约简为3项,若求得某振动信号的方根幅值、歪度和裕度离散集为{110},则诊断齿轮发生轮齿断齿,离散集为{011}或{001}时,判断齿轮箱发生轮齿磨损。 表3 决策规则表Tab.3 Parameters of decision rule 属性约简得到的最优解并非唯一解,遗传算法每次寻优结果均不唯一,不同求解结果理论上不影响最终诊断效果。例如:利用遗传算法再次重复上述约简试验,可以求得新的最简特征参量集{C1,C7,C9},该属性集同样可以作为故障诊断知识库。 为验证基于粗糙集和遗传算法属性约简得到的决策规则表的有效性,利用MATLAB对决策规则表进行验证试验。对每种故障类型分别选取40组数据作为故障实例,诊断数据分别提取均值、方根幅值、歪度及裕度4项故障特征。为验证该方法得到的不同决策规则表在故障诊断中具有普适性,设置{方根幅值,歪度,裕度}以及{均值,歪度,裕度}两组决策规则分别进行故障诊断,检验诊断结果是否准确。 图8为故障诊断结果,通过图8可以看出,基于属性集{C6,C7,C9}以及{C1,C7,C9}知识库的诊断过程中,分别存在3例和4例的误判。对于诊断过程中的误判,考虑在进行属性约简过程中所取不同故障类型的信号组数太少,最终得到的决策表知识库不完整,导致诊断过程中产生误判。 因此在原试验基础上,将约简信号组数从3组增加到6组,保持试验参数不变,重复上述试验,得到诊断结果如图9所示。从图9中可以看出,基于属性集{C6,C7,C9}和{C1,C7,C9}的新决策规则表的诊断率均达到100%,证明该方法能准确有效地判断打捆机齿轮箱故障的发生和类型。 (a)基于3组信号的{C6,C7,C9}属性集 (a)基于6组信号的{C6,C7,C9}属性集 通过上述对自走式打捆机齿轮箱故障诊断试验,证明了基于粗糙遗传算法的故障诊断方法在打捆机齿轮箱故障诊断中的有效性,利用约简得到的决策表不仅能判断故障是否发生,并且能准确地诊断齿轮箱的故障类型。 1)本文针对打捆机齿轮箱故障诊断过程中故障特征参量多的问题,采用了粗糙集理论实现特征参量集的约简,并根据约简后得到的决策表建立了诊断规则,实现故障诊断。 2)传统粗糙集约简方法在处理大型数据时存在效率低、依赖先验信息等问题,本文采用自适应遗传算法对属性集进行了约简,有效提高了算法运行效率且无需先验信息。 3)分别对轮齿断裂、磨损、轴承内外圈磨损等故障状态下的打捆机齿轮箱进行了信号采集,并将粗糙遗传算法应用于故障信号的诊断,对算法的有效性进行验证分析。分析结果表明:基于粗糙遗传算法的故障诊断方法有效实现了打捆机齿轮箱故障特征参量的约简,将初始决策表的12项故障特征参量约简为3项。分别利用约简得到的2组决策规则进行了故障诊断,诊断率均为100%。 4)该方法能够在无先验信息的条件下实现了属性约简,获取了最简故障特征参量,特征集的简约性和对故障的敏感性符合监测需求,为齿轮箱故障监测提供科学的监测指标,同时基于决策规则表的故障知识库能准确完成故障诊断,有效提高了打捆机的可靠性。
1.2 基于自适应遗传算法的属性约简

2 打捆机齿轮箱故障诊断试验
2.1 建立初始决策表


2.2 决策表属性约简
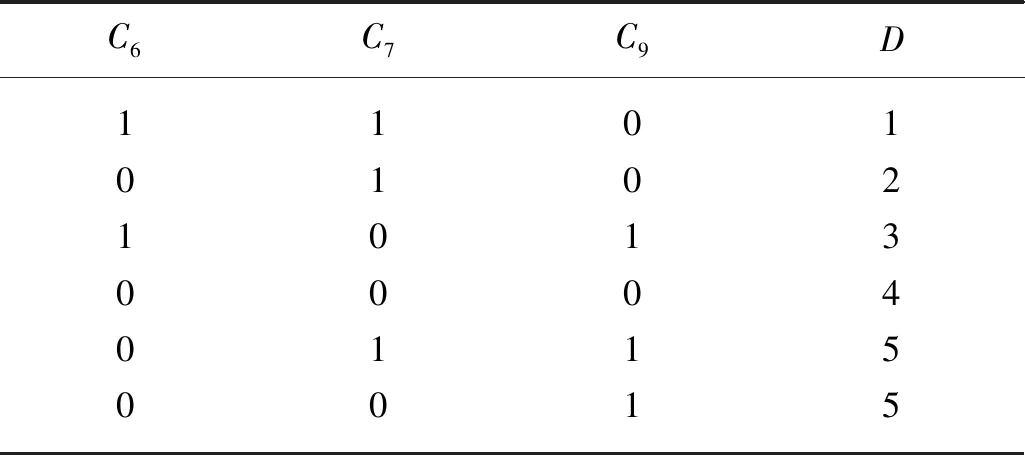
2.3 决策规则验证
3 结论

