一种优化相关性模型的机器人精度补偿方法*

程思渺，田 威，李 波，廖文和

（1.南京航空航天大学，南京 210016；2.南京理工大学，南京 210094）

随着“中国制造2025”战略的提出与推进，智能制造已经成为我国当前航空制造业发展的必然趋势[1-3]。随着工业机器人技术的发展，航空航天等领域逐渐出现机器人取代人工作业的趋势[4]，然而工业机器人绝对定位精度低已经成为制约其在高精度领域应用的首要因素。因此提升工业机器人的绝对定位精度对推动航空制造技术及发展有着重要意义和实用价值。

机器人精度补偿分为闭环补偿和离线补偿两种，闭环补偿在众多应用中都能获得出色的精度提升效果，但增加闭环补偿技术可能会造成闭环系统不稳定[5-7]。此外，在实际应用中，闭环反馈补偿技术需要通过激光跟踪仪等设备实时采集机器人误差，这就要求机器人的工作环境不会阻碍误差数据的采集。因此，该补偿技术的应用场景相对有限[5-7]。离线补偿技术无法达到在线闭环反馈补偿的高精度水平。然而，它相对来说更稳定，更可靠，更容易实现。其所能达到的精度水平也能满足机器人的大部分应用要求[7-8]。

传统的离线精度补偿方法主要是运动学标定[9-11]，通过标定相关参数，得到修正后的机器人运动学模型替代理论模型。然而运动学标定仅考虑几何参数引起的误差，因而精度补偿效果有限。为解决上述问题，许多研究人员建立了包含非几何误差源的模型。

基于误差相似度的建模方法是近年来机器人精度补偿的研究热点。周炜等[12]发现距离较近的两点具有空间相似性，划分空间网格后通过网格顶点误差对内部点实现了内部点位误差插值。石章虎等[13]利用空间相似性补偿移动制孔机器人的绝对定位误差。Zeng等[14-15]沿用这一思想将笛卡尔空间的相似度转换到关节空间，同时构建了误差相似度模型。何晓煦等[16]通过试验验证了机器人残差的误差相关性，并对残差构建误差相似度模型。Tian 等[17]通过在机器人关节安装光栅尺消除关节误差，同时对剩余误差用误差相似度模型进行补偿。Cai 等[18]在误差相似度模型的基础上设计了偏移变量对算法进行改进，使用普通克里格法取得了较好的补偿效果。Chen 等[19]将误差相似度与径向基神经网络相结合，进一步提高了机器人精度。上述方法均取得了较好的补偿效果，证明相似度模型能够在机器人精度补偿上有着较好的应用。然而上述方法忽略了相关性模型的选取对机器人定位精度的影响，本文对此展开研究。

本研究提出了一种优化相关性模型的机器人精度补偿方法，并通过KUKA KR500-3 机器人对该方法进行验证。

1 工业机器人误差相似度模型

假设n自由度旋转关节机器人的m个样本，其中，位置误差集合ε=[e1，…，em]T，其中。对于一组确定的关节输入，第l个方向的位置误差el（θ）可以由回归模型F和随机过程z组成：

其中，F（β:,l，θ）是关于θ的函数：

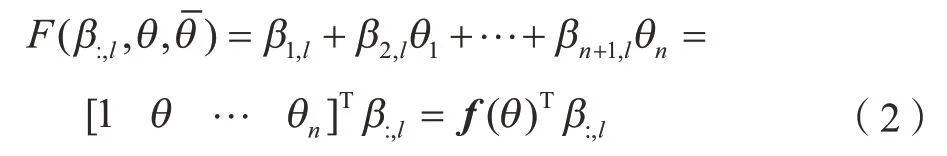
其中，β:,l是待拟合的参数，随机过程zl（θ）均值为零，方差为：

其中，E为数学期望；是第l个方向的过程方差；R（ξ，w，x）是关于参数ξ的相关性模型，该模型将在第2 节介绍。

通过已知样本集合建立误差预测模型：

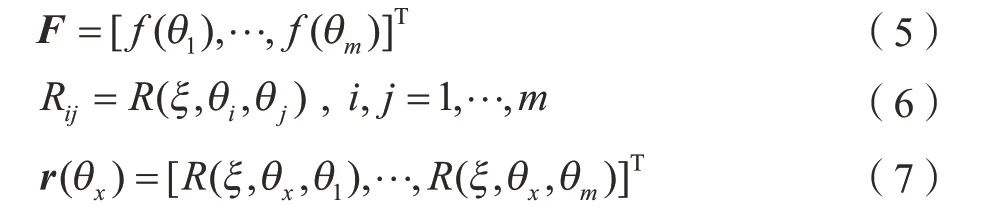
其中，F为f扩充得到的矩阵。

则预测误差和实际误差的差值可表示为：

其中，Z=[z1，…，zm]T，为了保证预测误差无偏性，有：

在此条件下，均方差为：

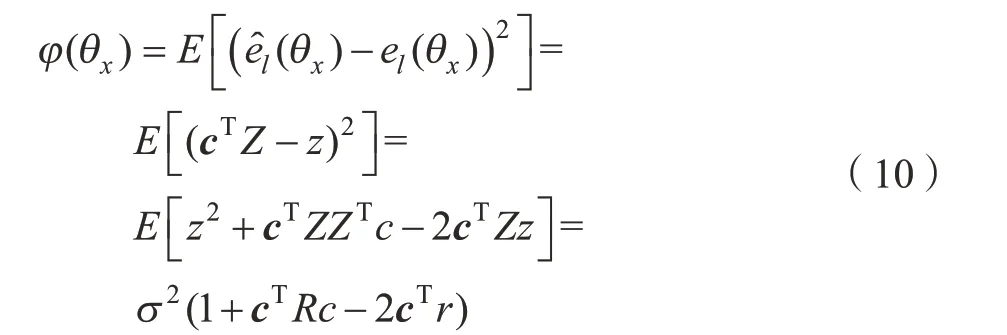
为获取目标点位的最优估计，应保证预测方差最小，式（9）作为已知条件，使得式（10）数值最小，由此建立拉格朗日方程：

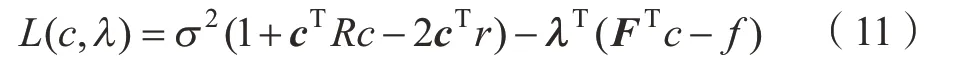
其中，λ是拉格朗日乘数，方程对c的偏导数为：

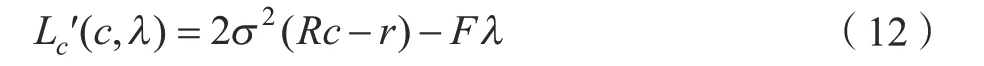
式（12）为0 时，式（11）取值最小，将方程的解代入式（4）可得：

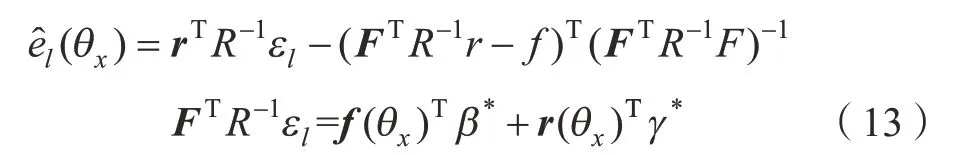
其中，β*=（FTR-1F）-1FTR-1ε为Fβ≈ε的最大似然估计值，其对应预测误差的方差的最大似然估计为：

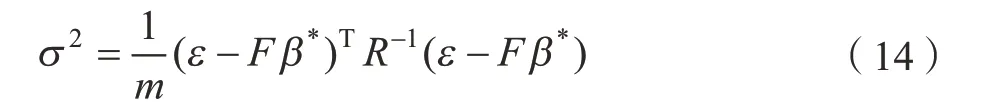
R、β*和σ2取决于参数ξ，设ξ*是ξ的最大似然估计值，ξ*的选取应使下式最大化：

|R|是矩阵R的行列式，根据式（3）中ξ优化获得ξ*[20]，代入到式（13）中，并由式（13）对机器人误差进行预测。

2 相关性模型选取

2.1 机器人定位误差的相关性分析

机器人定位误差的相关性可以用半方差函数定量分析，位置误差的半方差函数是工作空间内两个关节位置误差增量方差的一半，半方差函数通常是由一组样本的位置误差的经验半方差函数得到：

通过精度补偿试验测得的机器人定位误差数据得到图1所示的半方差函数图，可以看出，定位误差在x、y和z3 个方向存在各向异性，且变化趋势接近线性，为衡量定位误差与关节转角间的相关性程度，引入Person相关系数计算公式如下：

图1 机器人定位误差的半方差函数Fig.1 Semi-variance function of robot positioning error

计算可以得到3 个方向的Person 相关系数分别为0.9838，0.9918 和0.9543。可见3 个方向上定位误差与机器人关节所处位置有极强的线性关系。

2.2 各类相关性模型

在第1 节中构建了机器人的误差相似度模型，然而，对于式（3）中的误差相似度模型文献[10-15]均选取gauss 模型：

相关性模型的选取对工业机器人的误差相似度模型的拟合精度有着很重要的作用，为证明这一点，本节就不同的相关性模型对补偿后的机器人定位精度的影响展开研究，除gauss 模型外，常见的相关性模型如下。

exp 模型：

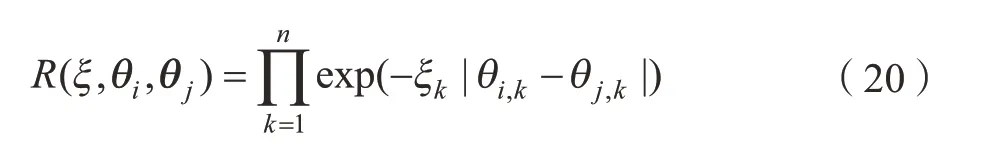
expg 模型：

lin 模型：

spherical 模型：

cubic 模型：

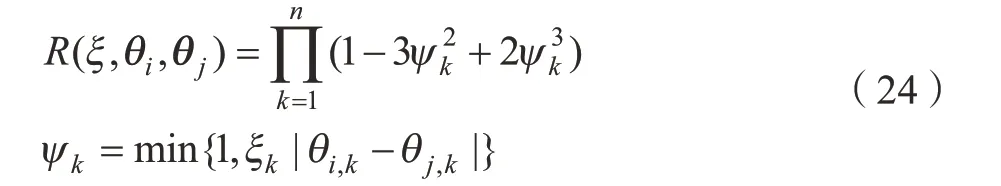
spline 模型：

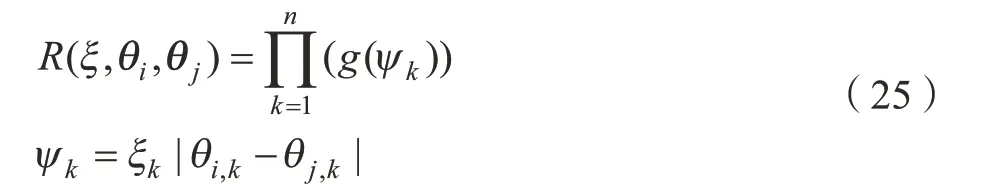
式中

2.3 仿真试验

为证明选取不同相关性模型，机器人补偿效果不同，本节建立仿真环境。通过精度补偿试验中采集到的500 个点的实际位置和关节角度进行机器人校准[21]，得到的D-H参数表如表1所示。

表1 修正后的D- H 参数表Table 1 Revised D- H parameters

以修正后的D-H参数为仿真环境下的真实参数，以理论的D-H参数为仿真环境下的理论参数。对于仿真环境中的点位，其误差为实际到达位置与理论到达位置的差值。以精度补偿试验采样的500 个点作为仿真环境下的采样点，并得到这些点的实际误差，同时在测量空间内随机生成5000 个点作为验证点，通过选取不同的相关性模型构建不同的误差相似度模型，分别对这5000 个点为进行精度补偿，补偿后机器人误差分布如图2所示。

图2 为补偿后5000 个点中>0.05mm 的点位误差分布图，可以看出在仿真环境下，各类相关性模型均能使工业机器人精度有较大的提升，且spline 模型补偿效果最高，体现在该模型补偿后的5000 个点误差均在0.05mm 内；同时cubic 模型补偿效果最差，体现在误差>0.05mm 的分布点位最多，各类相关性模型补偿后的统计数据如表2所示。

图2 不同模型补偿后>0.05mm 的综合误差Fig.2 comprehensive error >0.05mm after compensation of different models

从表2 中可以看出，在仿真环境中，spline 模型表现最优，体现在补偿后最大值为0.0411mm，远小于其他各类相关性模型。而cubic 模型效果最差，体现在补偿后标准差为0.0203mm，远大于其他模型的标准差，因而误差分布较为分散，同时其补偿后最大值0.2865mm 为几组模型中误差最大值。

表2 仿真环境下补偿后误差样本统计Table 2 Error sample statistics after compensation in simulation environment mm

从仿真试验中可以得出，不同相关性模型在补偿仅由运动学几何参数引起的误差时差异性较大。多项研究表明，由几何误差引起的位置误差约占整个机器人位置误差的80% ～ 90%[22-24]。仅靠仿真环境中建立的几何误差模型并不能完全证明在实际情况中能选取spline 模型作为最优模型，因此在下文对7 种模型进行试验验证。

3 试验验证与分析

3.1 试验平台建立

搭建图3所示的试验平台对机器人定位误差补偿方法进行试验验证。试验验证载体为KUKA KR500- 3 型号机器人，其法兰盘上装有制孔装置，测量设备为API Radian 激光跟踪仪，激光跟踪仪靶球安置在刀柄的靶标座上。机器人的重复定位精度为± 0.06mm，激光跟踪仪的绝对测距精度为15μm+0.7μm/m。

试验前需构建各类坐标系转换关系，由于基坐标系不可以直接测量，因此通过旋转轴线法得到，通过单独转动A1轴和A2轴分别得到圆O1和O2，由此建立基坐标系。建立基坐标系需要得知基坐标系的原点，x轴上一点和z轴方向。

z轴方向：转动A1轴，拟合得到圆O1，该圆周法向即为z轴方向。

原点：圆O1所在平面平移至圆O2圆心，再向下平移1045mm 得到基坐标系xoy平面，将圆O1圆心向基坐标系xoy平面投影，得到原点。

x轴上一点：圆O2所在平面平移至圆O1圆心位置，得到基坐标系yoz平面，圆O2圆心向该平面投影后再向基坐标系xoy平面投影，得到x轴上一点。

根据机器人示教器面板确定法兰坐标系位姿，构建法兰盘坐标系。设工具坐标系的原点为靶球中心点，姿态为基坐标系姿态，得到TCP 相对于法兰的转换关系，各坐标系统一关系由此确立。

3.2 精度补偿试验

在机器人的工作空间中规划了一个尺寸为550 mm×1000mm×1100mm 的长方体区域作为本次试验验证的测量区域，通过拉丁超立方[25]采样方法随机生成500 个点作为采样点位，采样点位置（x，y，z）在该长方体区域内随机选取，3 个姿态角（a，b，c）在[-5°，5°]、[-3°，3°]、[-3°，3°]内随机选取。以理论位姿为NC 指令控制机器人运动至上述随机采样点的位置，并用激光跟踪仪测量各采样点的实际位置。选取第2 节中不同的相关性模型进行精度补偿，补偿结果如图4所示。

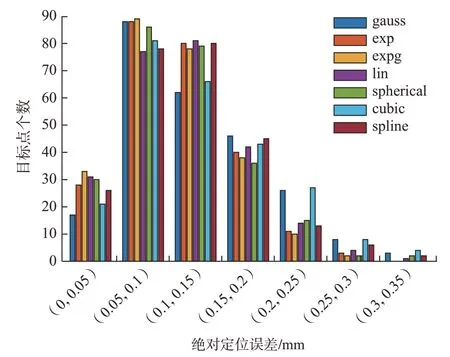
图4 KUKA KR500-3 补偿后综合误差Fig.4 Comprehensive error after KUKA KR500-3 compensation

从图4 可以看出，7 种相关性模型均能有效地补偿工业机器人的绝对定位误差。gauss 模型和cubic 模型误差分布较为分散，峰值较低，补偿效果相对较差。expg 模型误差较大的个数最少，效果相对较好。相应的统计学参数记录在表3 中，可以得出以下结论。

表3 机器人精度补偿后样本统计Table 3 Sample statistics after robot accuracy compensation mm

（1）7 种相关性模型均能有效地提高机器人的绝对定位精度。体现在未校准的机器人误差最大值为1.8057mm，而7 种模型均能使其最大值降低至0.35mm以内，定位精度能够满足航空航天中制孔装配等需求；且补偿后的均值均由1.1759mm 降低到0.13mm 内，标准差均由0.2743mm 降低到0.07mm 内，表明误差补偿后定位误差集中的位置更小，集中度更高。

（2）expg 模型在本次试验中较其他的相关性模型补偿效果更好。体现在补偿后的最大值为0.2902 mm，为7 种模型中补偿后最大值的最低值。且补偿后各点位的误差均值在0.1066mm，标准差在0.0502mm，均为几组数据中最小的，体现出expg 模型能使补偿后的定位误差集中的位置最小，集中度最高。

（3）cubic 模型和文献[14-19]采用的gauss 模型较其他的相关性模型补偿效果较差。体现在gauss 模型和cubic 模型补偿后误差最大值分别为0.3448mm 和0.3476mm，超过0.34mm，平均值均超过0.12mm，标准差超过0.06mm，而其他相关性模型均在该数值数据之内，可以证明这两种方法数据样本的集中位置和集中度均不如其他集中模型。

通过将仿真试验和试验对比可以发现，最差的模型在两组环境中表现出一致性，cubic 模型无论是在仿真环境还是试验环境中较其他模型均有较差的表现，对于cubic 模型是否在其他种类机器人中有着较优的表现有待验证。另外，两种环境下的最优模型不同。这是因为在仿真环境中，仅补偿运动学几何参数引起的误差，所以spline 模型有着较好的拟合效果，而在实际环境中，除几何参数引起的误差外还有非几何参数引起的误差，而对于该部分误差，expg 模型有着较好的补偿效果。

以上研究结果证明了KUKA KR500-3 选取优化后的相关性模型可以取得更好的补偿效果，但由于不同的工业机器人自由度不同，几何构型不同等原因可能会导致相关性模型选取上存在差异，因此实际工作中还需要针对具体的机器人进行具体的分析和检验，其具体流程如图5所示。

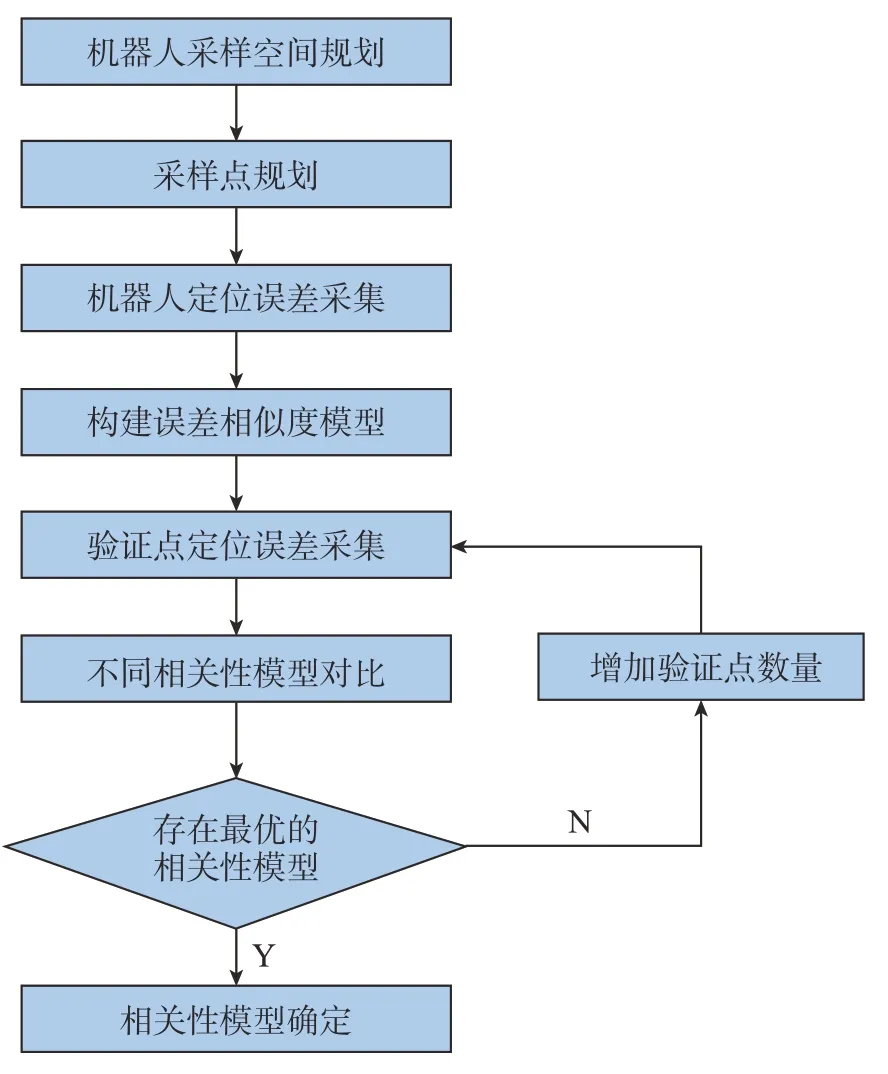
图5 相关性模型选取流程Fig.5 Correlation model selection process

4 结论

（1）通过在仿真及试验中构建不同的误差相似度模型对机器人精度进行补偿，证明了相关性模型的选取对会对机器人精度补偿效果有显著影响。

（2）在仿真环境中通过选取不同相关性模型对机器人运动学误差补偿，证明了spline 模型对机器人运动学误差的补偿效果最优，补偿后剩余误差仅有0.04mm。

（3）在机器人精度补偿试验中通过选取不同相关性模型对机器人进行实际误差补偿，证明了expg 模型对机器人运动学误差的补偿效果最优，可以使机器人精度从1.8057mm 达到0.2902mm。

（4）与传统gauss 模型相比，本研究选取的expg 模型精度在试验环境中的精度补偿效果可从0.3448mm提升到0.2905mm，精度提升15.75%。