电阻点焊缺陷超声信号多特征优化试验研究*

黄 宏，吴 玮，2，李坤航，杨宏睿，殷相杰，蒋启明，邓展鹰

（1.重庆理工大学，重庆 400054；2.重庆市特种焊接材料与技术高校工程研究中心，重庆 400054）

电阻点焊是轨道交通、汽车、精密仪器、飞机制造中金属板连接的主要工艺之一[1-2]，其连接质量直接影响产品的服役性能，因此对点焊质量进行检测是产品制造过程中一个非常重要的环节。点焊后质量检测方法主要有破坏性试验和超声检测[3-5]。其中超声波检测主要通过回波信息获取熔核尺寸、焊接缺陷等信息，实现对接头质量的无损检测。目前绝大多数电阻点焊超声检测标准是基于对熔核直径的定量化评估[6]，即建立焊点力学性能与熔核直径的关系，实现点焊质量的评价。以熔核直径做标准存在一定的局限性，一方面，当熔核内部无缺陷时，熔核直径相同，其厚度上可能会有差别，力学性能会有不同；另一方面，当熔核内部存在缺陷时，即使熔核直径相同，不同类型的缺陷也会使焊点的拉剪强度出现差别。因此，用熔核尺寸评估点焊质量并不全面，还需要判断熔核有无缺陷，并对缺陷的性质进行识别与评估。

合理提取特征值是准确识别缺陷及其类型的关键。超声波检测常使用回波的时域和频域信息做检测特征。如赵欣等[7]通过分析点焊缺陷回波时域幅值衰减率、波峰间隔和曲线峰态值等特征值参量，采用峰值标记识别算法对虚焊进行快速识别。Xiao 等[8]以获取缺陷回波的相位和振幅为主要特征，对夹杂物和空洞进行区分。樊萍等[9]利用小波包变换获取裂纹缺陷时频信号，通过自定义多类特征参数，取得较好识别效果。在对某类缺陷识别时，缺陷回波最佳特征值的选择与提取非常困难，通常凭经验捕获缺陷的多维特征集来对不同缺陷进行区分，容易出现冗余特征相干扰识别效果，因此需要对多维特征进行优选，剔除冗余相，提高缺陷识别的准确性。

电阻点焊内部缺陷通常有虚焊、气孔、缩孔、裂纹、喷溅等，目前对点焊多缺陷超声检测信号特征提取方法的介绍，以及多类缺陷识别研究的报道较少[10-11]。本研究针对铝合金电阻点焊气孔、未熔合和无缺陷试样，首先研究用经验模态分解对超声回波信号进行降噪重构，避免缺陷信息与干扰噪声发生混叠，提高信号信噪比，然后对重构后的缺陷回波信号分别进行时域、频域的多尺度特征值提取，之后分别采用主成分分析法（Principal component analysis，PCA）和线性判别分析法（Linear discriminant analysis，LDA）剔除冗余、无效的特征向量，对多维特征进行优化，最后结合BP 神经网进行实例验证，确定电阻点焊多维特征适宜的优化方法，实现对不同缺陷的准确识别。

试验材料选用规格为85mm× 25mm×2mm 的6061-T6 的铝合金薄板，用DTBZ-80 中频逆变直流点凸焊机焊接。通过调控焊接电流、时间、压力等参数，制备90 个含有气孔、未熔合、无缺陷等不同焊接质量的点焊接头，每种类型的接头各有30 个。采用15MHz 水浸聚焦探头进行检测。

基于经验模态超声信号重构

在信号检测过程中，被检测试件往往由于自身结构以及检测环境的影响，导致信号在传输以及接受的过程中，引入噪声造成超声信号的非平稳性以及信号的混叠，因此在特征提取之前需要对信号进行降噪。

经验模态分解（Empirical mode decomposition，EMD）不同于小波分析对基函数缺乏适应性，它是基于时频域的信号处理方法，能将采集的原始信号分解为一系列的固有模态函数（Intrinsic modal function，IMF）和一个残差。其中固有模态函数IMF分量是能够反映非平稳、非线性信号的时变频率的函数，具有表征信号局部特征的能力[12]。经验模态分解具体方法如下：

（1）找到原始信号X（t）的所有的极值点，并根据极小值与极大值拟合出上下包络线；

（2）计算均值包络线m（t），使得原始信号X（t）减去均值包络线m（t）得到中间信号r（t）；

（3）判断中间信号r（t），即IMF是否满足约束条件，其条件1 是在整个数据中极值点和过零点个数相等或相差不超过一个，条件2 是任意时刻时间轴对称，若不满足上述条件则返回第1 步反复迭代，直至满足约束条件，停止分解。通常残余分量记为res。

经过自适应算法处理后的数据，选取能够反映特征信息的本征模态函数，通常选取能量比累计率EPC（Energy proportion coefficient）≥95%时[13]，IMF 的最大阶数为k，将前k阶的IMF 进行重构即可得到表征缺陷信息的信号。

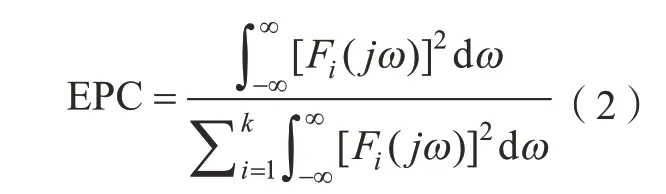
其中，Fi（jω）为超声时域信号的频率谱函数；i为IMF 的阶数次序；k为最大阶数。

对3 种典型缺陷超声回波信号进行重构，根据分解的IMF 成分图选取不同阶数的成分重构信号，如图 1所示，前5 阶IMF 高频分量集中了信号的主要成分，噪声成分较少，对于还原信号是有利的，且原始信号的能量主要集中在这几阶的IMF 中，具备表征信号特征的能力。

图1 EMD 分解的各阶IMFFig.1 EMD decomposition of each level of IMF

各阶能量占比见表 1，根据能量比率累积可知，当能量比累计率EPC≥95%时，可以此作为选取IMF分量的标准，能量主要集中在前k阶中，在本试验中3 种类型接头的k值分别为5、4、3 时，其EPC 达到95%，因此综合考虑选用前5 的IMF 模态函数进行信号重构。

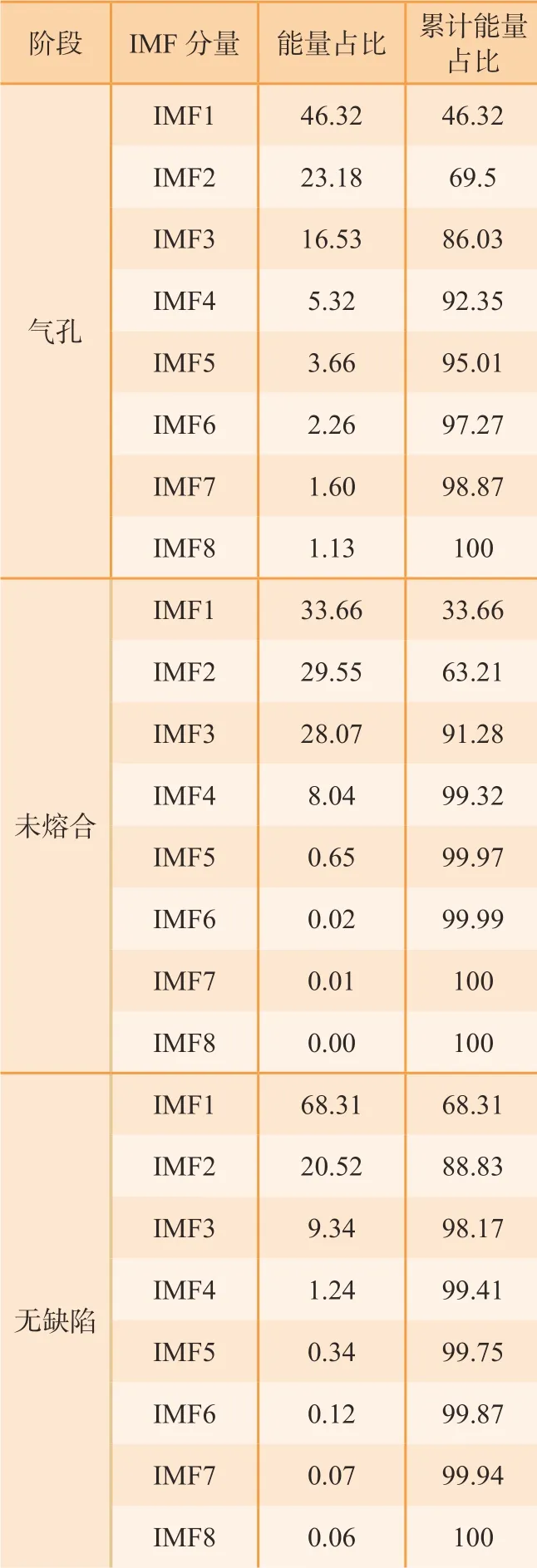
表1 各阶IMF 能量占比Table 1 Proportion of energy of each order of IMF %

图2 分别为3 种类型焊点的超声信号重构图，信噪比SNR 分别为23.965dB、23.288dB 和21.967dB，降噪重构后的信号无杂波，消除噪声与信号的混叠，平滑度得以改善，保留原始信号的振幅与趋势，有利于后续特征的提取。如图 2所示，气孔缺陷会造成能量的严重衰减，底面回波几乎消失；未熔合缺陷使超声波发生衍射造成衰减，但衰减程度较弱，底面回波清晰可见；无缺陷的试样不存在缺陷波，底面回波以及二次底面回波清晰可见。

图2 信号重构图Fig.2 Signal reconstruction diagram

信号多尺度特征提取

由于不同缺陷反射体对超声回波的影响和作用规律不同，超声回波信号的形状、幅值、频率都存在差异，单独从波形图上来辨别缺陷种类存在一定难度，且缺陷形状、走向也会在频域特征中做出响应。因此，对不同缺陷进行区分需要从时域、频域采用多尺度特征来对缺陷回波进行综合描述。

1 时域特征值提取

（1）缺陷回波包络特征（峰度Bk、偏度Sk、均值和方差Dx）。

回波包络中包含了超声回波信号的大部分信息，它在回波信号变化时呈现出不同的瞬态信息，如信号前沿、后沿的变化，尖峰位置，峰度和偏度等。峰度是指缺陷波分布形态陡缓程度的统计量，偏度用来描述缺陷回波分布对称性的统计量，均值和方差表示缺陷回波的集中趋势和离散程度，这些瞬态信息可以作为回波信号的识别依据。

通过材料内部传播的声速可以计算出熔核厚度和压痕深度，从而间接反映焊接质量，其计算公式为：

其中，V为材料内部声速；Ta和Tb为第1次和第2次底面回波的时间间隔。

（3）幅值系数K。

由于上层铝板反射回超声信号幅值与下层铝板反射回波幅值相差比较大，超声波在熔核内传播时遇到缺陷会发生衰减和散射，导致回波幅值降低，因此定义幅值系数K为一次表面回波振幅峰值Pa与二次底波振幅峰值Pb的比值，即：

（4）衰减系数α。

超声波在熔核内部传播时，遇到声阻抗不同的界面会产生散乱反射，从而引起衰减现象，散射衰减还与熔核晶粒大小密切相关，因此用衰减系数能够有效反映熔核内部缺陷特征，其计算公式为：

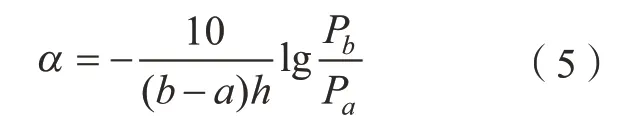
其中，Pa和Pb分别为一次和二次底面回波的幅值；h为母材界面厚度2mm。

对鸭坯进行统一前处理，之后进行烤制实验。具体为红外蒸汽烤制温度220℃，烤制时间30、35、40、45、50min，蒸汽喷射2次，分别为烤制的第10min和第30min，每次喷射时间为3s；最后红外干烤10min。

图3是气孔、未熔合和无缺陷频域波形时域特征参量变化规律图。可以看出，气孔缺陷由于回波波幅较高且形状尖锐，峰度最小值2.767远远大于未熔合和无缺陷两种类型；无缺陷接头在均值、偏度和方差3 类特征值中均高于其他两种接头，气孔、未熔合缺陷在偏度特征值中呈一定线性关系，其原因在于气孔和有效熔核体积的尺寸有关。3 种缺陷的衰减系数特征区分非常明显，气孔、未熔合和无缺陷的衰减系数分别集中在4.5、2.5 和1.5 左右，原因在于气孔是光滑的弧面且内部为焊接凝固过程中来不及挥发出的气体，其声阻抗差异很大，因此对超声波衰减存在较大影响；而3 种缺陷的幅值系数特征分布相对比较离散。

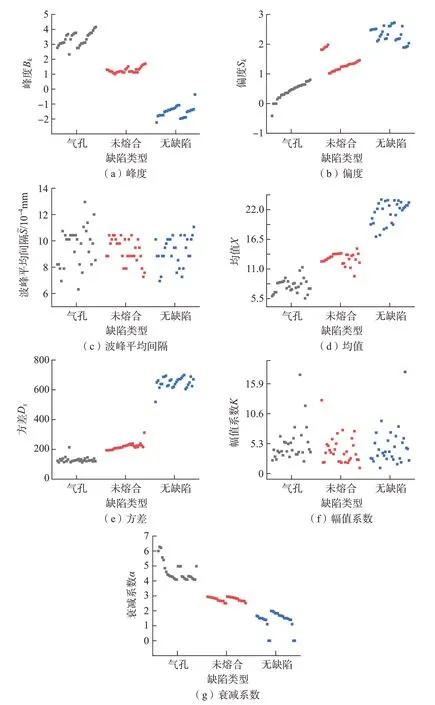
图3 缺陷时域特征值Fig.3 Time-domain characteristic values of defects

2 频域特征值提取

（1）低/高频段积分面积E1/E2。

由于不同类型的缺陷对于声波能量的衰减程度不同，即频谱图中所有的离散点的幅值存在差异，因此其能量系数也不同。定义0～10MHz 频率段的积分面积为低频段积分面积E1，10～20MHz 频率段的积分面积为高频段积分面积E2，采用积分的方法对离散点所构成曲线面积进行计算。

（2）功率谱主频率f和极大值A。

f反映信号简谐成分中幅值最大的简谐分量频率，表明该频率的简谐波能量最大，对原信号的贡献最大。A反映了主频率f简谐波的幅值大小，同时反映了信号最大频率简谐分量的衰减程度。

图4 是3 种信号的频域特征值变化规律。可见，各频段的能量分布受到缺陷形式的影响，缺陷的存在会造成低频部分发生响应，气孔缺陷在低频段聚集，面积积分E1在20 左右；反之，无缺陷在高频段发生聚集，面积积分E2在50 左右；功率谱密度定义了时间序列的功率如何随频率分布，不同的缺陷信号由于传播方式的不同，各信号的功率谱密度表现形式也有差异，从图 4 中可知，频域特征值可以作为特征向量。

图4 缺陷频域特征值Fig.4 Frequency domain characteristic values of defects

多特征优化

模式识别分类器的正确识别率往往是建立在多维特征的需求上，在这个要求下，原始特征空间或输入的特征值通常情况下维数是很高的，其目的是获取更加全面且密切表征缺陷信号的特征值。但这并不意味着特征空间越大越好，过多的特征向量造成分类规则的复杂化、计算时间过长以及识别准确率的下降，因此特征选取以及特征的降维就显得十分必要。从原始特征向量空间中，根据不同的分类规则选择最小、相关度高、相互独立的特征子集，剔除冗余与目标不相关的特征，从而达到更高的效率以及识别正确率，常用的方法有PCA 和LDA 等。

1 基于PCA 的特征优化

PCA 是最具代表性的降维方法之一，其主要通过找到最大方差值或最小重构误差的最优投影后进行特征提取和数据重构。对一组含有N维的特征值，通过线性变换使数据重新组合为K维（N>K）的无量纲数据组合，并计算各成分的贡献累计量，使得主要成分能够达到较高累计贡献量，将数据简单化[14]。PCA 分析步骤如下：

（1）设有1 组m个样本记为K，对样本进行标准化，得到样本矩阵R，其中Kij（i=1，2，3，…，m）。

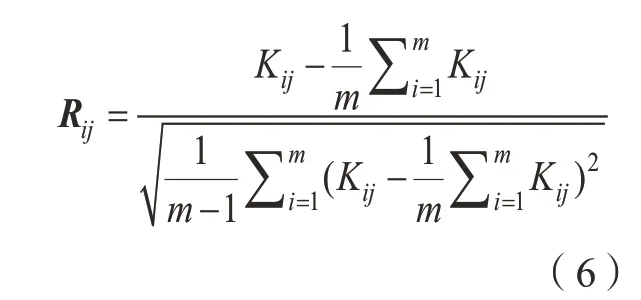
（2）计算其相关系数矩阵B。

（3）设特征值为λ，使相关系数矩阵B满足正交。

（4）计算主成分贡献率Ai和累计贡献率Ci，可由式（7）和（8）确定。

试验所用的特征值共有90×11的样本容量，PCA 优化分析结果如图 5所示。图5（a）显示随着主成分的数量增加其特征贡献率越低，说明后面的成分并不能表征缺陷的特征，为了避免信息的冗余，选取前两个主成分作为特征值。特征值及其贡献率和累计贡献率如表 2所示，对特征的表征贡献量达到99.97%，涵盖了超声信号的绝大部分信息，前两个特征值分布如图 5（b）所示，分类效果十分明显，因此选取前两个成分构成的90×2 的融合特征量矩阵作为分类器的输入。

表2 协方差矩阵特征值Table 2 Covariance matrix eigenvalues

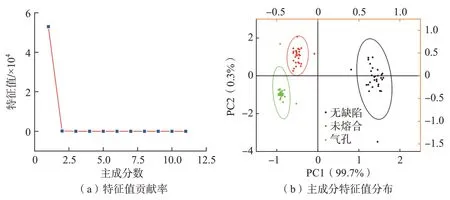
图5 特征值的PCA 分析Fig.5 PCA analysis of eigenvalues

2 基于LDA 的特征优化

LDA 是有督导的降维方式，而PCA 是无督导的降维方法，LDA 不仅可以用来降维还可以用于分类，其原理是对原数据进行降维投影，寻找出将各类最大程度区分的方向，即类间差平方和最大，总方差尽可能小。因此判别就是将数据向互不相关的特征向量上投影，线性判别可以降维至K-1（K为类别数），因此选用优异的判别函数可以起到降维作用，进一步将样本分类[15]。

采用LDA 计算特征值对样本进行统计降维，结果如表 3所示。根据缺陷类型以及数据特征计算出2 个判别函数，其函数积累为100%即说明这两个判别函数完全可以解释说明所有的样本特征信息，因此提取前两个函数作为后续的输入特征值，判别函数的分布见图 6。

图6 特征值的LDA 分析Fig.6 LDA analysis of eigenvalues

表3 判别函数摘要Table 3 Summary of discriminant function

实例验证及分析

对提取的90×11 的特征矩阵分别经过PCA 和LDA 降维后，均获得90×2 的联合特征向量。将气孔、未融合、无缺陷3 种类型定义编码分别为100、010、011，将样本数据归一化后做利用BP 神经网络的输入层，对其进行训练以及识别，选用trainscg作为传递函数，训练步数为1000，训练误差为0.001，学习速率为0.01。将原始特征值以及两种方法降维后的重组特征值分别作为输入值对比其识别准确率，其结果如表4所示，原始特征值情况下气孔的识别准确率较低，只有83.3%，而PCA 作用对两种缺陷的识别准确率均可达到100%，对无缺陷类型中存在1.1%的错误率，LDA 对气孔和无缺陷的识别准确率为100%，但未熔合缺陷只有95%，综合比较PCA 的降维方法取得了更好的识别效果。

表4 BP 神经网络分类结果准确率Table 4 Accuracy rate of BP neural network classification results %

结论

（1）3 种缺陷回波信号经EMD分解得到8 阶IMF 分量，气孔、未熔合以及无缺陷等原始信号的能量集中在前5 阶，对前5 阶IMF 模态函数进行信号重构，信噪比可提高21dB左右。

（2）分别提取重构信号的时域回波包络特征、波峰平均间隔、幅值系数和衰减系数，以及频域段的面积积分和功率谱频率和幅值为特征值，3 类信号特征都有明显的分布规律，其中回波包络特征、衰减系数和频域特征量与气孔、未熔合以及无缺陷有较为准确的对应关系。

（3）经过PCA 和LDA 两种降维方法构造后的特征量，与未经过降维的特征量相比，具有更好的分类结果，其中PCA 作用效果更好，对两种缺陷识别准确率均为100%；对无缺陷类型中存在1.1%的错误率，而基于LDA 降维方法构造后的特征量与未经过降维的特征量，各类缺陷识别准确率均高于原始特征量。