异形发射药结构设计与计算验证
高宇晨,胡 睿,周 敬,张玉成,杨伟涛
(西安近代化学研究所,陕西 西安 710065)
引 言
发射药是身管武器中弹丸运动的能量来源。具有更长的发射距离、更高的初速一直是该领域研究人员追求的目标[1]。改变发射药的几何形状以获得更高的装药密度和燃烧渐增性是调整弹道性能的常用方法。发射药药粒多为单孔、7孔或19孔的圆柱形颗粒,被广泛应用于大炮或火炮[2]中。目前新设计的几何形状有PSS(程序劈开杆)[3]、片状多层结构[4-7]和MPD(超多孔圆片)[8]等。
内弹道性能的模拟大多依据发射药燃烧表面面积来计算燃烧压力和弹丸速度。现有内弹道模型中的形状函数可以实现对常规发射药药粒表面积随着燃烧深度而变化的计算[9]。为计算复杂结构的发射药燃烧表面积变化以满足内弹道模拟计算的需求,学者们进行了诸多研究[10]。但对于特殊几何形状的发射药没有形式函数可以使用,尤其是对于特殊几何形状的燃烧表面积变化、体积变化以及燃烧渐增性研究较少,阻碍了内弹道模拟的研究。
因此,本研究采用几何切割的方法,计算了发射药的表面积、体积及燃气生成猛度。设计了多种特殊形状的发射药,对计算结果进行了比较。最后,利用密闭爆发器试验对设计的12孔三角形发射药的燃烧性能进行了验证。
1 计算方法
为简化计算,做如下假设:
(1)发射药燃烧服从几何燃烧规律,在t=0时刻,所有发射药粒同时燃烧;
(2)发射药粒不可压缩,且形状尺寸均匀一致;
(3)发射药燃气按理想气体处理,高温燃气成分及物理化学性质保持固定不变;
(4)D为药粒宽度,mm;d为药粒孔径,mm;c为药粒长度,mm;k为长宽比,k=c/D;N为发射药药粒总孔数;e为药粒已燃厚度,mm;2e0为弧厚,mm;Ψ为发射药已燃百分数,Ψ=已燃烧体积/初始总体积;σ为相对燃烧表面,σ=(初始总面积-t时刻总面积)/初始总面积;Z为相对厚度,Z=e/e0。
1.1 几何计算药形原理
目前已有发射药形状函数主要应用于带状药、多孔圆柱形火药及多孔花边火药等,对于更加复杂的药形,形状函数建立困难,难以适用于非传统发射药面积体积计算中。R. D. Anderson[11]首次报道了用于表面和体积计算的几何计算过程,其将复杂药形切割,通过对切分后每部分进行独立面积及体积计算,最后整体加和的方式,建立了与计算机运算相结合的发射药面积及体积计算方法。由于计算过程中,切分后每部分计算相对独立,具有灵活性,可满足复杂异形结构发射药药形设计的需求。
以21孔三角形柱状发射药(图1)为例,可将发射药药粒等分为25个等边三角形、3个扇形和15个长方形,见图2。通过计算每根长条的端面积及侧面积,乘以条数和颗粒长度,可计算长条的面积及体积,进而得到发射药颗粒的总表面积及总体积。
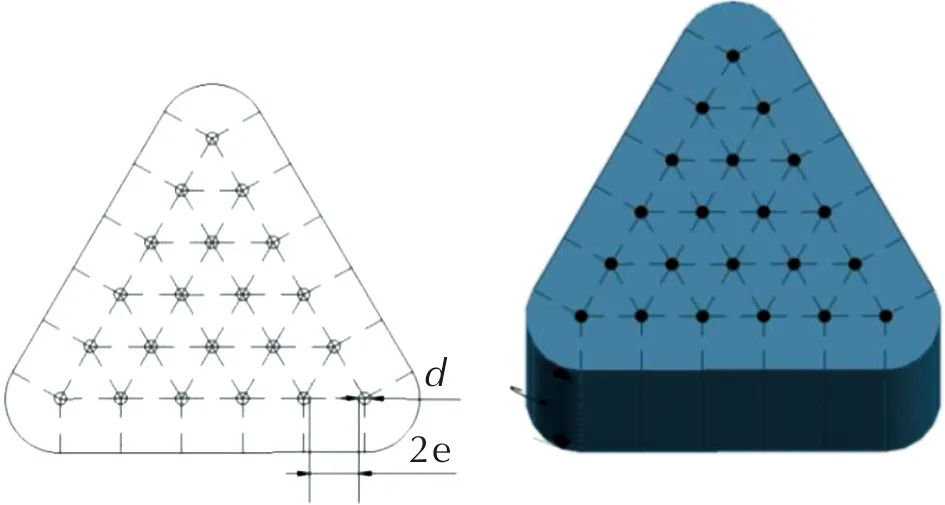
图1 21孔三角形发射药几何切分示例Fig.1 Example of geometric segmentation of 21-pore triangular propellant

图2 几何切分得到的长条示例Fig.2 Diagram of strips obtained by geometric segmentation
1.1.1 圆形柱状或扇形柱状长条的计算原理
圆形柱状或扇形柱状长条需要4个参数进行面积和体积计算:内径、外径、弧形角度和长条长度。由图2(a)可见,外径为线段OA,长度为DOA;内径为线段OB,长度为DOB;弧形角度为∠BOC,根据几何关系可推知燃烧外边缘长度LBOE,内穿孔长度LBPE,截面积SEND,分别可通过式(1)~(3)计算得到:
LBOE=∠BOC×DOA
(1)
LBPE=∠BOC×DOB
(2)
SEND=0.5×(DOA×LBOE-DOB×LBPE)
(3)
随着燃烧深度的加深,DOA变短,DOB增长。当DOB≥DOA时,长条烧穿。
1.1.2 三角形长条的计算原理
三角形柱状长条端部面积计算可利用已有的燃烧面积计算方法,形状见图2(b)。
1.1.3 长方形长条的计算原理
长方形柱状长条端面如图2(c)所示,将长方形以线段EF为对称轴等分为长方形ABFE和长方形EFCD进行计算,直至穿孔彼此相交。两个长方形对称,以长方形ABFE为例进行说明,根据几何关系进行计算,其中,穿孔半径为DBQ,燃烧外缘长度为LBOE=LAE,燃烧穿孔弧长为LBPE=0.5×π×DBQ。
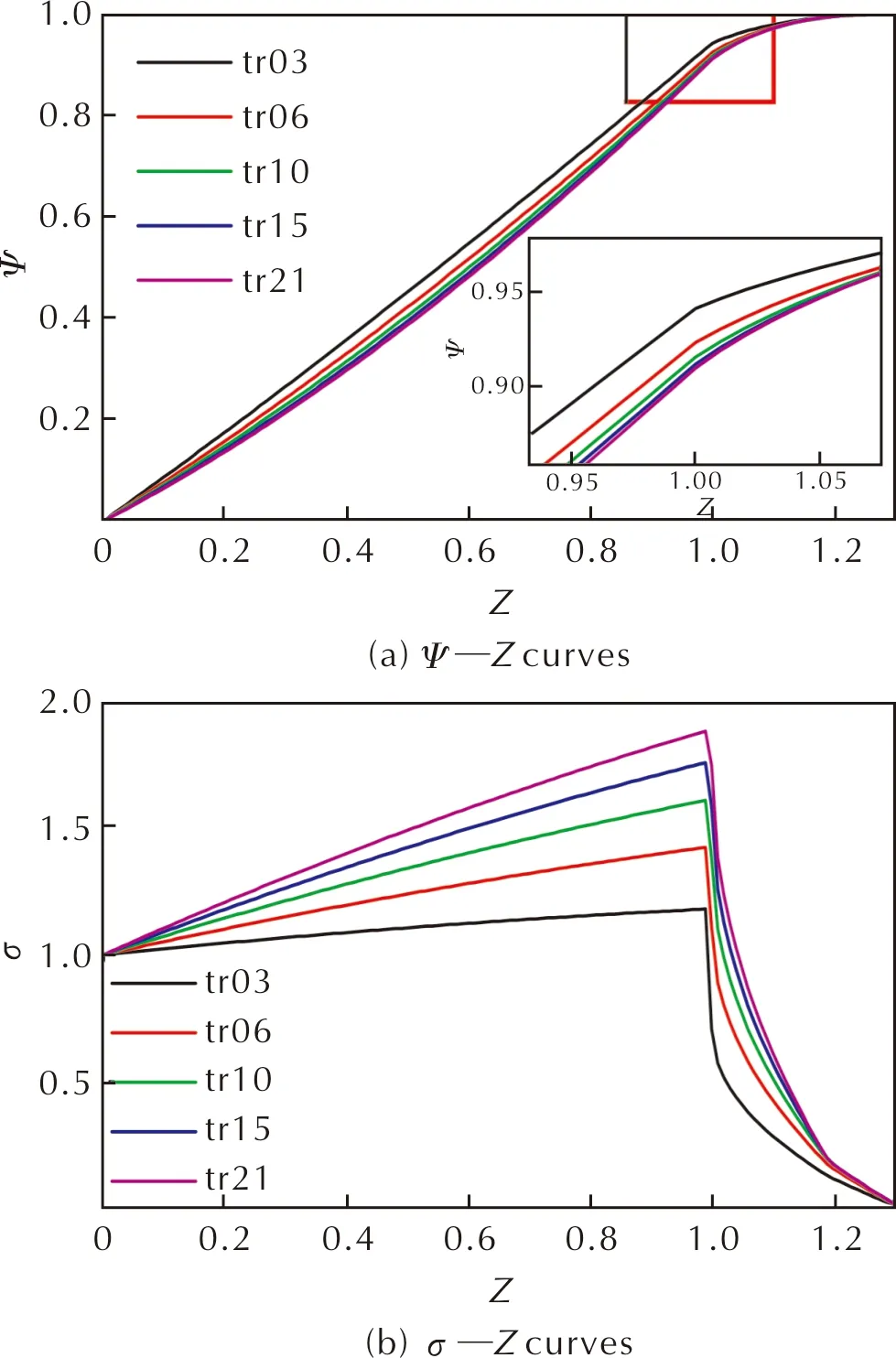
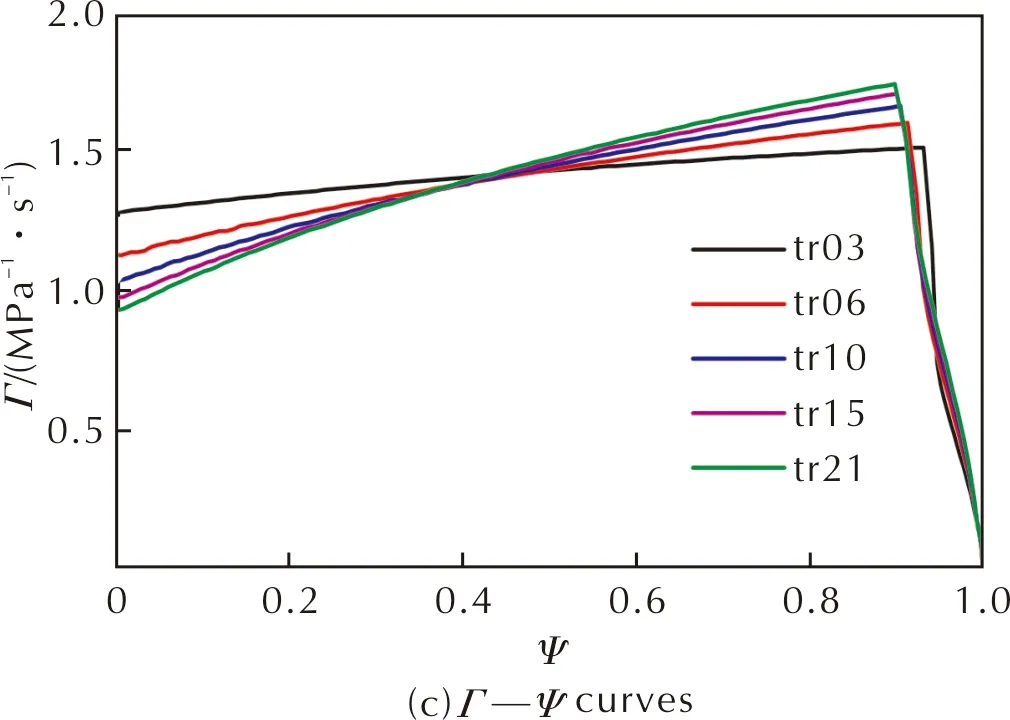
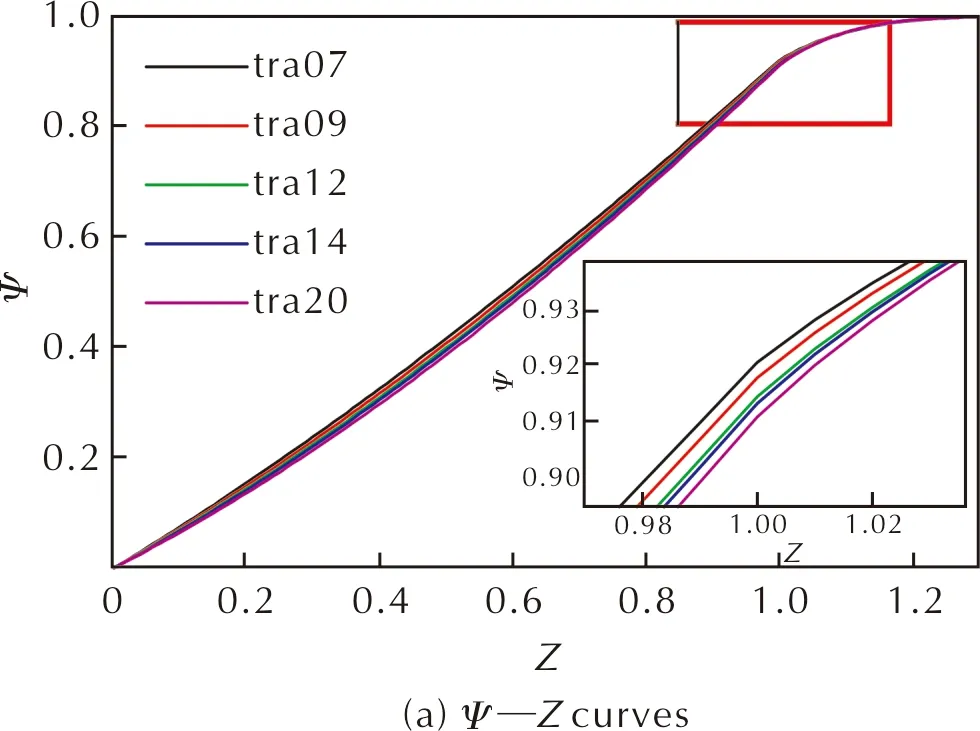
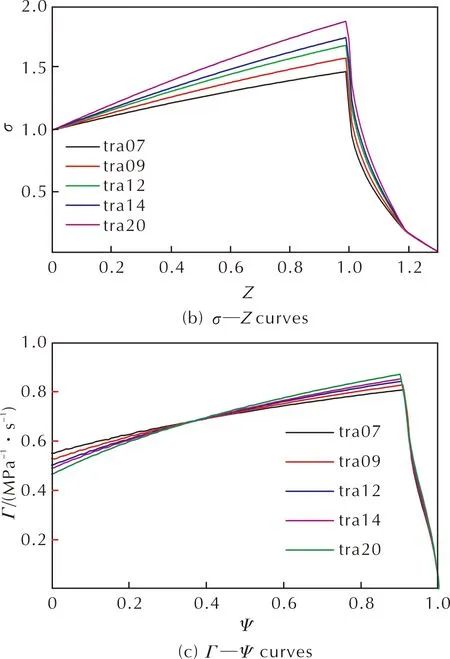
需检查燃烧外缘与穿孔弧是否相交,应比较LBA′和LBP的大小。当LBA′ (4) 根据发射药药形设计中孔径与弧厚比值的不同,进一步燃烧时可分为两种情况: (1)当发射药药形最外圈穿孔边缘垂直到外边缘的距离大于或等于弧厚时,如图2(e)所示,燃烧外缘与穿孔弧相交。此时,燃烧穿孔弧长为: (5) 燃烧外缘: (6) 端部面积减少量: (7) SENDS=0.5×(LBPE×LBQ+LA′B×LA′Z+LBF×LFQ) (8) 随着燃烧深度增大,当LA′B≤LFQ时,发射药烧穿,总面积和总体积均为零。 (2)当发射药药形最外圈穿孔边缘垂直到外边缘的距离小于弧厚时,如图2(f)所示,燃烧外缘与穿孔弧相交。此时,燃烧外缘及燃烧穿孔弧长为: (9) (10) 端部面积减少量: SENDS=0.5×(LA′B×LA′Z+LBPE×LBQ) (11) 随着燃烧深度增大,发射药烧穿,总面积和总体积均为零。 由于长方形ABFE和长方形EFCD关于线段EF对称,可以计算得到双孔方形ABCD随着燃烧深度变化的总表面积和总体积。 为准确地分析发射药在燃烧过程中的燃烧表面变化规律,通常利用Γ—Ψ曲线进行研究。Γ值的变化趋势可以反映发射药在燃烧过程中燃烧面的变化规律。 (12) 根据1.1节对发射药面积与体积计算原理,结合计算机编程形成计算软件,可计算得到σ—Z曲线及Ψ—Z曲线。利用式(12),计算得到不同孔数的异形发射药的Γ—Ψ曲线。 图3 不同孔数三角形柱状发射药示意图Fig.3 Diagram of triangular propellants with different pore numbers 通过上述切分原理,经过几何计算可以得到不同孔数三角形柱状发射药的Ψ—Z曲线和σ—Z曲线,见图4。 图4 不同孔数三角形柱状发射药的模拟燃烧曲线Fig.4 Simulated combustion curves of triangular propellants with different pore numbers 图4(a)中多孔发射药已燃百分数随着相对已燃厚度的增大而增大,且经过分裂点后增长趋势开始减缓。在已燃厚度相同的情况下,药形设计中孔数越多发射药已燃百分数越小,且分裂点的已燃百分数随着孔数的增加而略微增加。由图4(b)可以看出,随着相对已燃厚度的增加,由于两者的孔内燃烧面增加的速度大于孔外燃烧面减小的速度,多孔发射药均呈现出明显的增面性。在曲线转折点之后,发射药中孔已烧穿,留下三角形长条继续燃烧,因此整体呈减面燃烧效果。由图4(c)可知,5种三角形柱状发射药的燃气生成猛度都呈上升趋势,并且随着孔数的增加上升趋势愈发明显。这是由于多孔发射药燃烧过程中存在孔内燃面增加与外层燃面减少,随着孔数的增加,孔内燃烧发挥的影响越大,增面燃烧占据主导,表现出燃面渐增性燃烧。 保持内外弧厚与药粒孔径一致,分别设计不同孔数的四边形柱状发射药药形进行计算。选取孔数分别为6、9、12、15、20的四边形柱状发射药(分别用para06、para09、para12、para15和para20表示)进行模拟计算,对应内外弧厚为2mm,药粒孔径为0.5mm,药粒长度为20mm。假设四边形发射药孔数为N,则N=f(n)=n横×n纵,其中n分别为横向和纵向的排数。且四边形柱切分后长方形长条的数量为N长=(n横+n纵-2)×2,圆弧长条数量为N弧=4。切分后横截面如图5所示。 图5 不同孔数平行四边形柱状发射药示意图Fig.5 Diagram of parallelogram propellants with different pore numbers 图6(a)、(b)为不同孔数四边形柱状发射药燃烧面积及体积随已燃厚度变化曲线,发射药已燃百分数随着已燃厚度与初始燃烧弧厚之比的增大而增大,在临近分裂点时减缓,且已燃百分数随着孔数的增多而减小。图6(c)中不同孔数的四边形柱状发射药均体现出增面燃烧,且随着孔数的增加燃气生成猛度增长更快,规律性变化趋势与多孔三角形柱状发射药相近。 图6 不同孔数的四边形柱状发射药的模拟燃烧曲线Fig.6 Simulated combustion curves of quadrilateral propellants with different pore numbers 图7 不同孔数梯形柱状发射药示意图Fig.7 Diagram of trapezoidal propellants with different pore numbers 通过计算获得了具有不同孔数的梯形柱状发射药的Ψ—Z曲线、σ—Z曲线及Γ—Ψ曲线,见图8。 图8 不同孔数梯形柱状发射药的模拟燃烧曲线Fig.8 Combustion simulation curves of trapezoidal propellants with different pore numbers 可以看出其变化规律和三角形柱状发射药及四边形柱状发射药基本一致。在相同已燃厚度时,发射药随着孔数的增加已燃百分数变小,相对燃烧面积增加,Γ—Ψ曲线表明其在分裂前呈现增面燃烧趋势,在转折点之后由于孔烧穿,呈现出减面燃烧效果。 保持内外弧厚及长宽比一致,改变异形发射药药粒孔径,研究药粒孔径对其燃烧渐增性的影响。以15孔三角形柱状发射药为例,分别取孔径为0.3、0.4、0.5、0.6、0.7mm进行计算。对应发射药药粒内外弧厚为2mm,药粒长宽比为0.7,药粒宽度以三角形横截面穿过中心的高的长度度量。 图9为不同孔径时15孔三角形柱状发射药的Ψ—Z曲线、σ—Z曲线及Γ—Ψ曲线。 图9 15孔三角形柱状发射药的模拟燃烧曲线Fig.9 Simulated combustion curves of triangular propellants with 15 pores 图9(a)中在已燃弧厚与初始燃烧弧厚之比小于0.8之前孔径越大的三角形柱状发射药在相同燃烧厚度时燃烧百分数更大,而临近分裂点时燃烧减缓,孔径较小的发射药在分裂点处发射药已燃百分数更大。由图9(c)可知,不同孔径的三角形柱状发射药燃气生成猛度随着燃烧百分数的增加都为上升的趋势,且随着孔径的减小,上升趋势愈明显,分裂点逐渐后移,与文献报道结果一致[2]。整体来看,孔径大小对15孔三角形柱状发射药的燃烧过程影响有限,不同孔径的15孔三角形柱状发射药的Ψ—Z曲线近乎重合,Γ—Ψ曲线中燃气生成猛度增长速率相差不大。 利用密闭爆发器试验对本研究提出的发射药药形计算模型进行试验验证。按照GJB770B-2005 703.1密闭爆发器试验方法测试试样药粒性能。密闭爆发器容积106mL,装填密度0.33g/cm3,点火药为2号硝化棉,点火压力10MPa,试验温度20℃。 图10 12孔梯形柱状发射药的Γ—Ψ曲线Fig.10 Γ—Ψ curves of trapezoidal 12-perforated propellant 按照Γ—Ψ测试曲线的变化,将曲线分为4个区段分析:I阶段为发射药逐渐引燃阶段,Γ测试值从某一最小值Γ0开始,迅速上升达到最大,表明在试验中引燃过程是逐渐而非瞬时的。在经典内弹道学理论[12]中,火药引燃过程的逐渐进行已经被证实。Γ测试值上升到最大值时相当于装药表面完全引燃,装药表面的不同时引燃以及装药药粒不同步燃烧导致在完全引燃瞬间弧厚的差异性,并且会反映在火药燃烧的最后阶段。II阶段为陡升达到最大后逐渐下降阶段。I、II阶段的存在多出现在挥发性溶剂的硝化棉配方中,在成型过程中,火药表面留下空隙以及残留挥发物在药粒厚度中分布不均匀,导致燃速系数u1实际上不是常数,表面较大而深入到发射药内部后逐渐均匀,因此实际测试Γ在起始阶段超过理论值,出现上升和下降阶段。 III阶段为火药内层燃烧阶段,在图10中Γ—Ψ测试曲线和计算曲线差别明显,在Γ—Ψ测试曲线中引燃阶段结束后,Γ首先保持了一段规律燃烧然后递减,且曲线中没有明显的分裂点,而按照理论计算,Γ—Ψ计算曲线保持增面燃烧直到明显的分裂角点。在内弹道学研究[13]中,曾指出火药空道内部燃烧和外部燃烧条件不同造成的孔内外压强差是这种燃烧现象的基本原因:在几何假定条件下,药粒所有表面燃烧是在相同压强下以同一速度进行的,然而,在实际中火药燃烧过程发展极快,装药的不同部分和个别药粒的压强无法及时平衡,在不同位置的燃烧表面单元是处于不同压强以不同速度进行燃烧。因此,由于压强差的存在,气体受到其作用以大速度沿孔道表面流动形成气流,导致实际火药的燃烧表面相比按照几何燃烧定律计算得到的减小更迅速,表现出Γ测试值相对于计算值降低,多孔杆状发射药中气流效应对燃烧现象的影响十分复杂,在进一步研究中可结合现有数值模拟手段[14]进行探讨。 IV阶段为急速下降阶段。Γ—Ψ测试曲线相比于计算曲线下降转折点提前,其主要原因同I、II阶段分析因素相同,即是由于实际药粒引燃不一致以及尺寸不均一,因此导致药粒的燃尽及分裂时间不一致。 综上,与经典内弹道理论中分析管状药、七孔药以及36孔吉斯涅姆斯基药粒等标识曲线类似,本文设计的多孔发射药的Γ—Ψ测试曲线与根据几何燃烧定律计算的Γ—Ψ计算曲线偏离,其主要是由于实际燃烧过程中受到点火一致性、药粒尺寸分布以及燃烧过程中孔道压强差等因素综合影响。 (1)通过几何计算的方法,将发射药切分为三角形长条、方形长条、扇形长条,对切分部分进行独立计算。可广泛适用于不同药形发射药的药形结构设计,并用于燃烧面积、燃烧体积、燃气生成猛度的计算。 (2)设计了多种异形发射药(三角形柱状发射药、四边形柱状发射药及梯形柱状发射药),经过计算发现多孔异形发射药理论燃面及燃烧百分数随燃烧过程进行变化过程相近。对设计的异形发射药理论计算的燃烧特性曲线进行了研究,均呈现出燃烧渐增性,且随着孔数的增加燃气生成猛度升高更迅速。 (3)异形发射药在内外弧厚保持一致,长宽比保持不变的基础上,孔径取0.3、0.4、0.5、0.6、0.7mm时,均表现出燃烧渐增性,且孔径越小燃烧分裂点越靠后,与理论分析相吻合,且孔径变化对其燃烧过程影响有限。 (4)对12孔梯形柱状发射药进行了密闭爆发器试验,对比实验值与计算值,试样的燃气生成猛度曲线存在一定偏差。1.2 发射药燃气生成猛度的计算

2 异形发射药设计与计算
2.1 三角形柱状发射药燃烧面积与体积计算

2.2 四边形柱状发射药燃烧面积与体积计算
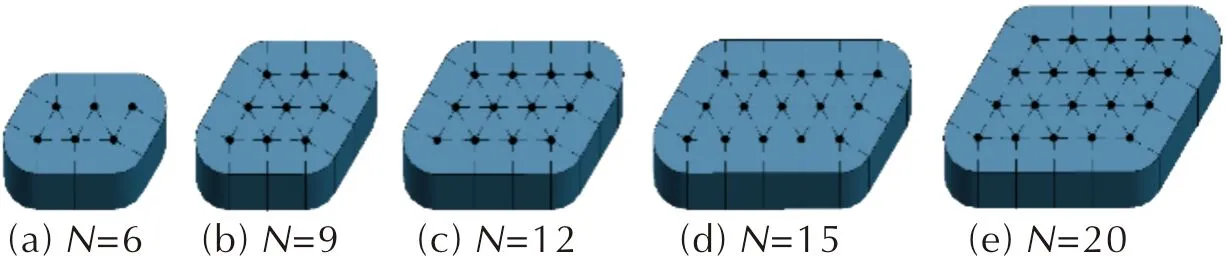

2.3 梯形柱状发射药燃烧面积与体积计算

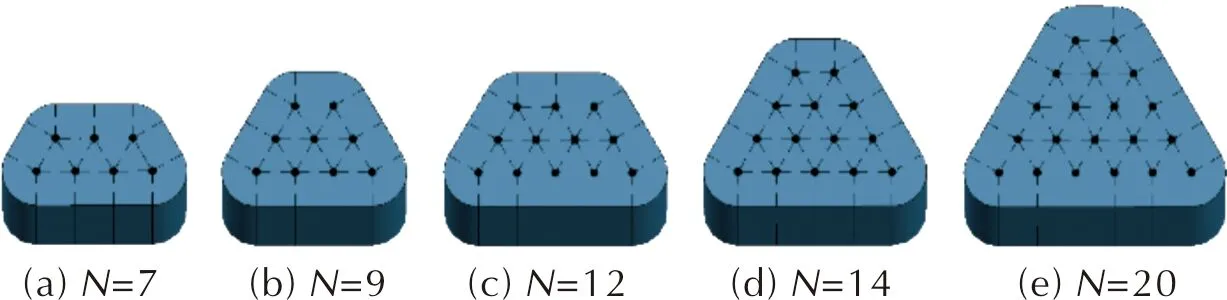
2.4 内孔径对异形发射药燃烧渐增性的影响

3 验证试验


4 结 论

