涉及轻质弹簧问题求解策略

■朱建强

弹簧是用弹性材料制成的器件,在高中阶段研究的弹簧多是质量可以忽略不计的轻质弹簧。轻质弹簧在外力作用下发生形变,产生的弹力的大小和方向满足胡克定律,除去外力后又能恢复原状。轻质弹簧既可以伸长也可以压缩,既可以施加(受到)拉力也可以施加(受到)支持力,但是轻质弹簧中的张力处处相等。遇到涉及轻质弹簧问题时,需要从轻质弹簧弹力的特性入手,正确分析研究对象的受力情况,综合判断研究对象的运动情况,结合平衡条件或牛顿第二定律完成解答。下面举例分析,供同学们参考。

一、轻质弹簧的弹力变化问题求解策略

因为弹簧的弹力与弹簧的形变量有关,弹簧的形变量发生变化需要一定的时间,所以弹簧弹力不能在瞬间发生突变。与之相对应的,轻绳和轻杆的弹力可以发生突变。求解轻质弹簧的弹力变化问题时,可以先在原状态中找到弹力,再在现状态中求出加速度,进而求解其他物理量。

例1 如图1所示,细绳一端拴一个质量为m的小球,另一端固定在竖直墙壁上,固定在同一竖直墙壁上的水平轻质弹簧支撑着小球,小球与弹簧不粘连。小球保持静止状态时,细绳与竖直墙壁间的夹角θ=53°,重力加速度为g,sin53°=0.8,cos53°=0.6。以下说法中正确的是( )。

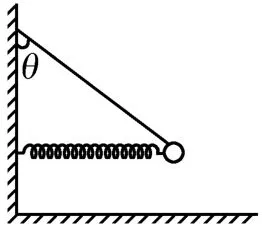
图1

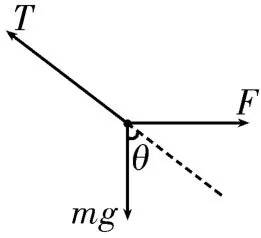
图2

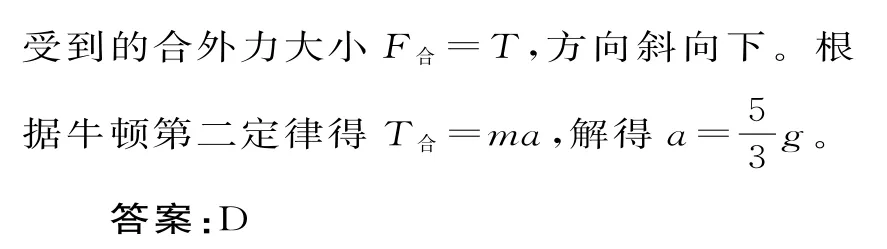
二、轻质弹簧的多解问题求解策略

弹簧既可以伸长也可以压缩,因此弹簧的弹力既可能是拉力也可能是支持力。在分析弹簧的弹力时,如果题目没有明确说明是哪种形变,那么就需要考虑伸长和压缩两种情况。

例2 如图3所示,一质量为m的木块,用劲度系数为k的轻质弹簧连接,弹簧的另一端固定在斜面顶端,木块放在斜面上能够处于静止状态。已知木块与斜面之间的动摩擦因数μ=0.6,斜面倾角θ可调节,弹簧始终在弹性限度内,最大静摩擦力等于滑动摩擦力,重力加速度为g,sin37°=0.6,sin30°=0.5。下列说法中正确的是( )。

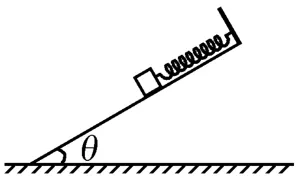
图3

A.若斜面倾角θ=37°,则弹簧可能处于压缩状态

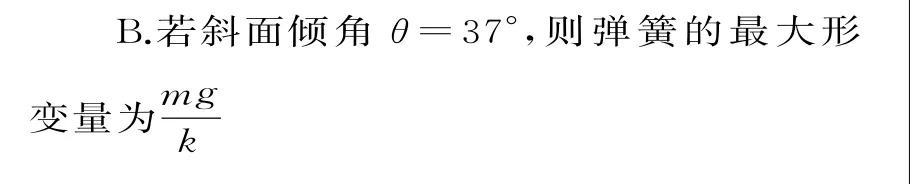
C.若斜面倾角θ=30°,则弹簧可能处于压缩状态

D.若斜面倾角θ=30°,则木块受到的摩擦力一定沿斜面向下

答案:C

三、轻质弹簧的临界问题求解策略

临界状态往往出现在一段过程的开始或结束时刻,因此求解临界问题需要先弄清研究对象的运动过程。

例3 如图4所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量分别为mA、mB,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态,重力加速度为g。现用一恒力F沿斜面方向拉物块A使之向上运动,求物块B刚要离开挡板C时物块A的加速度a和从开始到此时物块A的位移d。

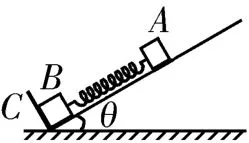
图4

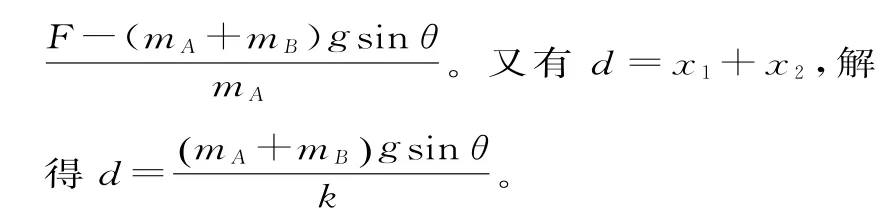
1.如 图5 所 示,质 量分别为m1、m2的A和B两物块用一轻质弹簧连接,放置在水平传送带上,水平轻绳一端连接物块A,另一端固定在左侧墙上,两物块与传送带之间的动摩擦因数均为μ,传送带沿顺时针方向转动。系统达到稳定后,在剪断轻绳的瞬间,设两物块的加速度大小分别为aA和aB(弹簧始终在弹性限度内,重力加速度为g),则( )。

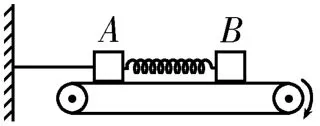
图5

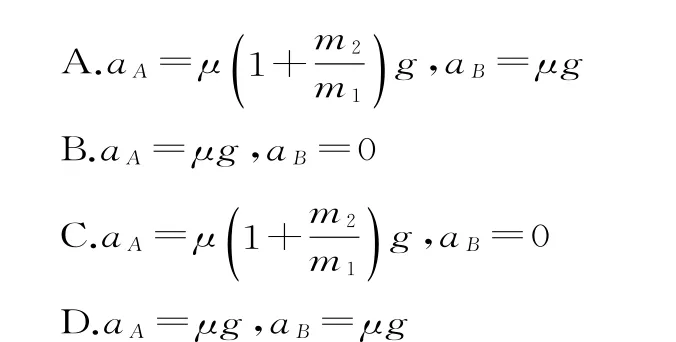
2.如图6所示,质量为m的质点与三根完全相同的轻质弹簧相连,静止时相邻两弹簧之间的夹角均为120°,已知弹簧a、b对质点的作用力均为F,则弹簧c对质点作用力的大小可能为( )。

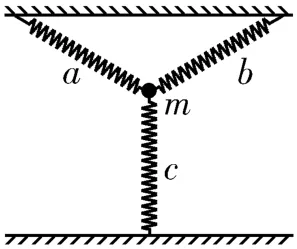
图6

A.0 B.F+mg

C.F-mgD.mg-F

3.如图7所示,A、B两木块叠放在竖直轻弹簧上,两木块的质量分别为mA=0.42kg,mB=0.40kg,弹簧的劲度系数k=100N/m,若在木块A上作用一个竖直向上的力F,使它由静止开始以加速度a=0.5m/s2竖直向上做匀加速运动(取g=10m/s2),求在这个过程中,力F的最大值。

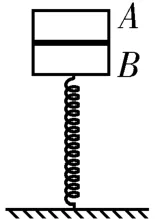
图7

参考答案:1.C 2.ABCD

3.Fmax=4.41N。