筒式武器铝合金堵盖打开机理研究

黄瑞杰，阮文俊，步鹏飞

(南京理工大学 能源与动力工程学院， 南京 210094)

单兵筒式武器系统通常包括发射筒、喷管、光学瞄准具和火箭弹等结构，而一部分单兵筒式武器会在喷管喉部安装堵盖来增强点火性能[1]。堵盖作为单兵筒式武器尾部喷管中的一个重要部件，主要起到2个作用：① 密封防潮，确保火药及点火药正常工作；② 建立点火压力，提高点火可靠性和稳定性[2]。

堵盖打开压力对单兵筒式武器点火过程、弹丸初速及火炮平衡影响较大，设计合理的堵盖打开压力关系到筒式武器发射过程的顺利进行。唐强[3]模拟分析了不同堵盖打开压力对固体火箭发动机燃烧室压力变化的影响；苏听听[4]比较了几种不同堵盖打开压力下的点火过程；余贞勇[5]模拟分析了不同喷管堵盖打开压力对翼柱型装药火焰传播时间的影响；豆松松等[6]对小型固体火箭发动机内流场进行一维数值模拟，发现火箭发动机在工作初期会发生震荡，堵盖打开压力越大则震荡次数越多。张秋芳等[7]设计了一种在圆周方向上开有相同的六个泄压孔的双层铝箔堵盖，研究在使用电点火头直接点燃火药和使用电点火管点火2种方式下堵盖的打开情况。Wang[8]将圆形堵片紧密安装在喷管喉衬和扩张段之间，采用整体爆破的方式打开来研究堵盖厚度与点火压力的关系，发现堵盖厚度越大则点火压力越大。还有许多学者通过数值仿真的方式对各种不同材质的堵盖打开过程进行研究，得到与试验相符合的结果[9-14]。

2A12铝合金作为一种武器系统中的常用材料，具有质量轻、易加工、强度高和打开一致性好的优点，将其作为堵盖材料对打开压力精度的控制效果较好。目前对打开压力精度有要求的情况下常采用复合材料层合板作为堵盖材料，但此类材料堵盖存在高温打开压力低、低温打开压力高的问题。因此本文设计了一种2A12铝合金堵盖和模拟试验装置，利用试验得到堵盖的打开压力，然后基于LS-DYNA建立2A12铝合金堵盖的有限元模型以及考虑其存在制造公差情况下的有限元模型，对其进行仿真计算得到打开压力与打开速度，并将仿真结果与试验结果进行比较。

1 堵盖结构设计

本文对2A12铝合金堵盖进行结构设计，整体结构形状呈拱形，分为支撑段、破坏段和凸起段3部分，其中凸起段又可分为凸起上升段和凸起平台段。

堵盖边缘为支撑段，起支撑固定堵盖的作用，堵盖打开时支撑段存留在炮尾内。堵盖中部设计凸起段，能以较低的厚度承受较大的压力载荷，可以有效减小堵盖重量，降低堵盖打开后的后喷危险界限。堵盖设计有4种不同有效厚度，区别在于破坏段的厚度(即有效厚度)不同，分别为0.4 mm、0.65 mm、0.9 mm和1.35 mm，有效厚度越大则堵盖强度越高。堵盖打开时破坏段破坏失效，凸起段与支撑段失去连接而分离。堵盖结构如图1所示。

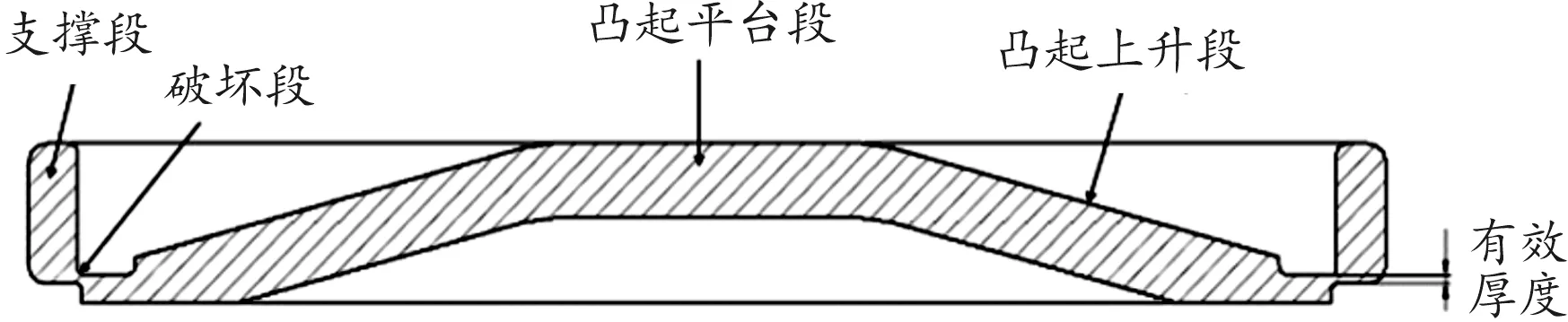
图1 堵盖结构示意图

2 堵盖打开模拟试验

2.1 试验系统设置

本文设计了一种专用于测试单兵筒式武器尾喷管堵盖打开过程的模拟试验装置。本试验装置的本体分为两部分，均为使用高强度炮钢制成的短圆筒，两部分使用螺纹连接。如图2所示。

图2 试验装置示意图

试验将模拟试验装置安装在固定钢架上，将堵盖安装在模拟试验装置本体中对应位置，将火药和点火器通过点火线相连接，安装2个测压传感器于试验装置两侧，测压传感器另一端通过导线与数据采集仪相连接，将数据采集仪通过导线与触发点火器相连接，在火药点火堵盖打开后通过试验装置后方口径70 mm的筒状开口飞出。

2.2 试验结果

4种有效厚度的堵盖各进行5发试验，共计20发。试验中每种堵盖均有两发后喷方向面对空地，其余堵盖后喷方向面对2 m外覆盖湿棉被的20 mm厚松木板。试验得到的打开压力如表1所示。

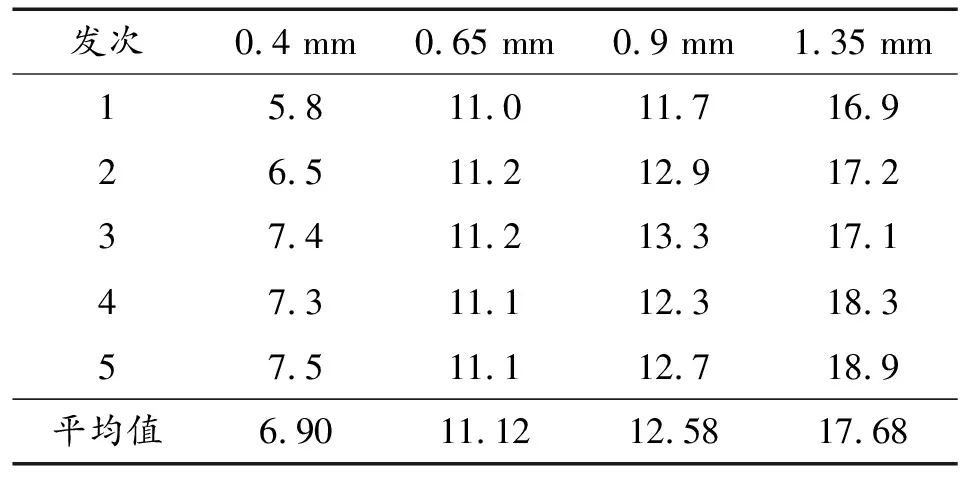
表1 堵盖打开压力统计表 MPa

从试验装置一端喷出后，2A12铝合金堵盖均破坏呈圆片状，圆片边缘不平整。堵盖在喷口朝向空地的情况下均飞出30 m以外，在喷口朝向覆盖湿棉被的松木板的情况下有多片击穿湿棉被和松木板，可见其具有较强的破坏能力和较大的后喷危险界限。

3 仿真计算

3.1 2A12铝合金本构模型

2A12铝合金材料本构模型采用Johnson-Cook本构模型，Johnson-Cook模型由Johnson G R和Cook W H于1983年提出[15]，是一种描述应变强化、应变率强化及温度软化效应的理想刚塑性本构模型，适用于大多数金属和合金材料。

Johnson-Cook模型的表达式如下：

(1)

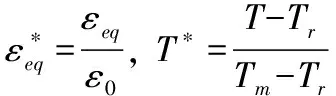
3.2 有限元模型

本文对4种破坏段厚度不同的2A12铝合金堵盖进行仿真分析，破坏段厚度分别为0.4 mm、0.65 mm、0.9 mm和1.35 mm。在进行仿真分析之前将模型进行简化，并建立一个筒状结构来支撑堵盖，代替直接的边界条件设置，将简化堵盖安装之后的截面如图3。

图3 堵盖截面图

在LS-DYNA中采用cm-g-μs单位制进行建模，用三维实体单元划分网格，将堵盖结构离散为4节点四面体单元，单元长度0.5 mm，并将筒结构离散为8节点六面体单元，软件自动划分生成网格。生成网格后的有限元模型如图4。

图4 堵盖有限元模型网格划分示意图

3.3 材料模型

2A12铝合金堵盖采用*MAT_SIMPLIFIED_JOHNSON_COOK模型来进行描述，此模型不考虑材料的温度软化效应，相关材料参数由简化的Johnson-Cook表达式来描述：

(2)

相关材料参数如表2所示。

表2 2A12铝合金堵盖材料参数

筒采用*MAT_RIGID刚体材料模型来进行描述，3个方向及旋转全部固定，相关材料参数如表3所示。

表3 筒材料参数

堵盖与筒的接触设置为面面接触，通过LS-DYNA关键词*AUTOMATIC_SURFACE_TO_SURFACE实现，将动静摩擦系数设置为0.1。

3.4 压力载荷设置

在实际射击或模拟试验装置试验过程中，膛内高压造成堵盖内外巨大的压力差，导致堵盖被打开。本文仿照实际情况，给堵盖内面施加压力载荷曲线，制造内外压力差。压力载荷曲线取自实际试验中压力传感器实测值，利用LS-DYNA关键词DEFINE_CURVE定义，如图5所示。

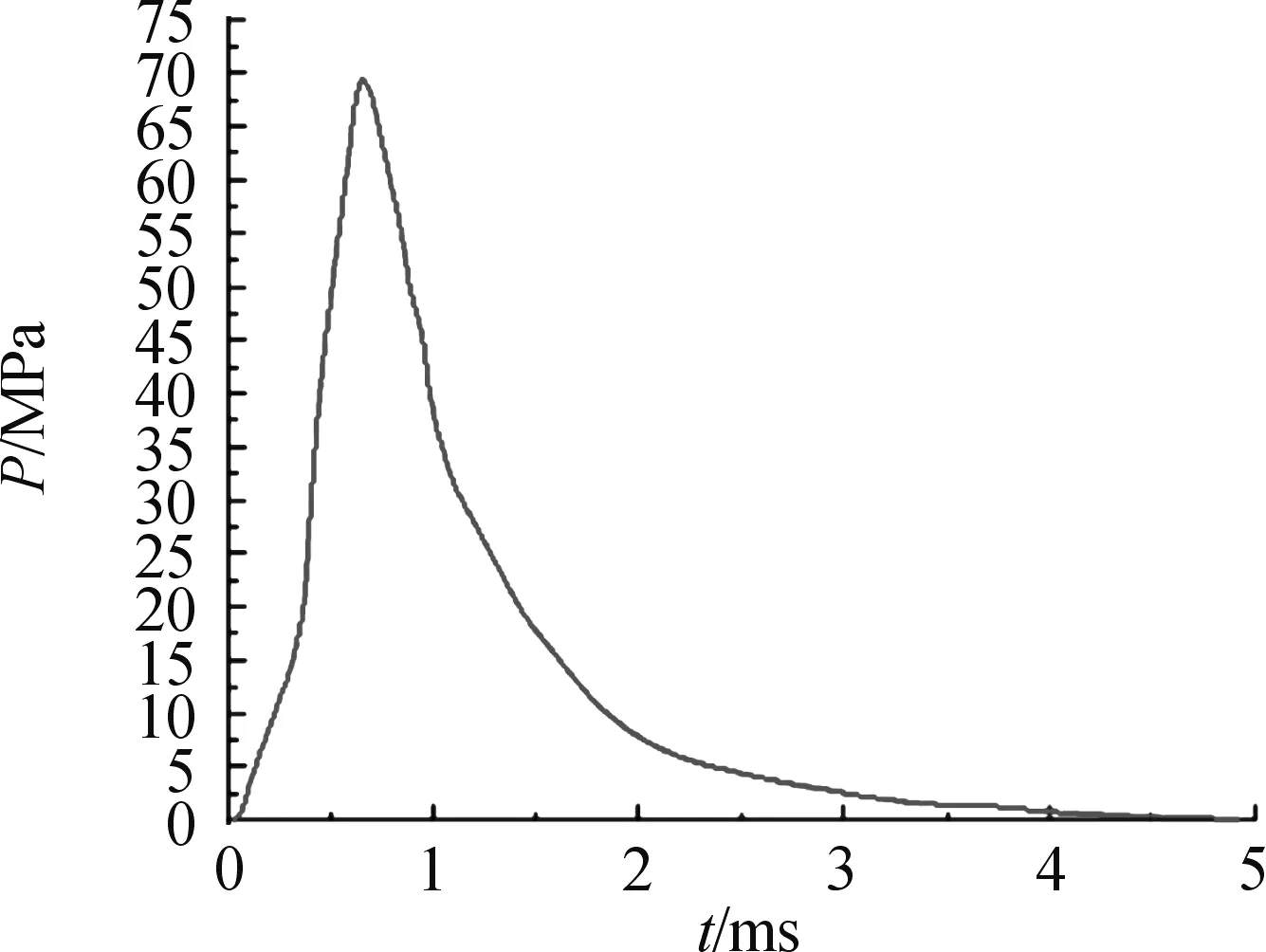
图5 压力载荷曲线

堵盖承压面在堵盖内面内选择，利用LS-DYNA关键词*SET_SEGMENT，选择承压面，利用关键词*LOAD_SEGMENT_SET将压力曲线施加在承压面上。

4 结果及分析

4.1 数值仿真结果

图6～图9表示了4种有效厚度的2A12铝合金堵盖在高压载荷下不同时刻对应的应力分布和发展情况，以及堵盖破裂打开的过程。0 μs时，开始对堵盖施加压力，此后堵盖上下两侧压力差逐渐增大，堵盖各处应力随之增加，堵盖单元未出现失效，应力逐渐集中到凸起斜坡段，凸起平台段周围应力处在较低水平。此后，到达图6～图9(a)所对应时刻时应力开始向破坏段集中，堵盖开始产生变形。图6～图9(b)所对应时刻为应力集中于破坏段，破坏段多处达到最大失效应变，单元开始失效消失的瞬间。图6～图9(c)所对应时刻为破坏段完全破坏，凸起段与边缘支撑段分离，堵盖完全打开的瞬间。

图6 有效厚度0.4 mm堵盖打开过程应力

图7 有效厚度0.65 mm堵盖打开过程应力

图8 有效厚度0.9 mm堵盖打开过程应力

图9 有效厚度1.35 mm堵盖打开过程应力

整个过程中，应力的最大分布逐渐从凸起斜坡段向外扩散，破坏段开始塑性变形，凸起段整体下沉，应力慢慢集中于破坏段，到堵盖完全打开时达到最大应力，而凸起平台段应力一直处于较低水平，结构变形也不明显。在仿真过程中，堵盖打开后，凸起段整体飞行较为平稳。堵盖打开后姿态如图10所示。

图10 堵盖打开姿态示意图

4.2 有效厚度对堵盖打开压力和速度的影响

在仿真计算过程中，将堵盖破坏段在圆周方向上所有单元的失效，即堵盖凸起段与支撑段的完全分离视为堵盖打开，这一时刻所对应的压力载荷即为堵盖的打开压力。有效厚度分别为0.4 mm、0.65 mm、0.9 mm和1.35 mm的堵盖，其打开压力有较明显的不同。将试验得到的平均打开压力与仿真结果如图11。

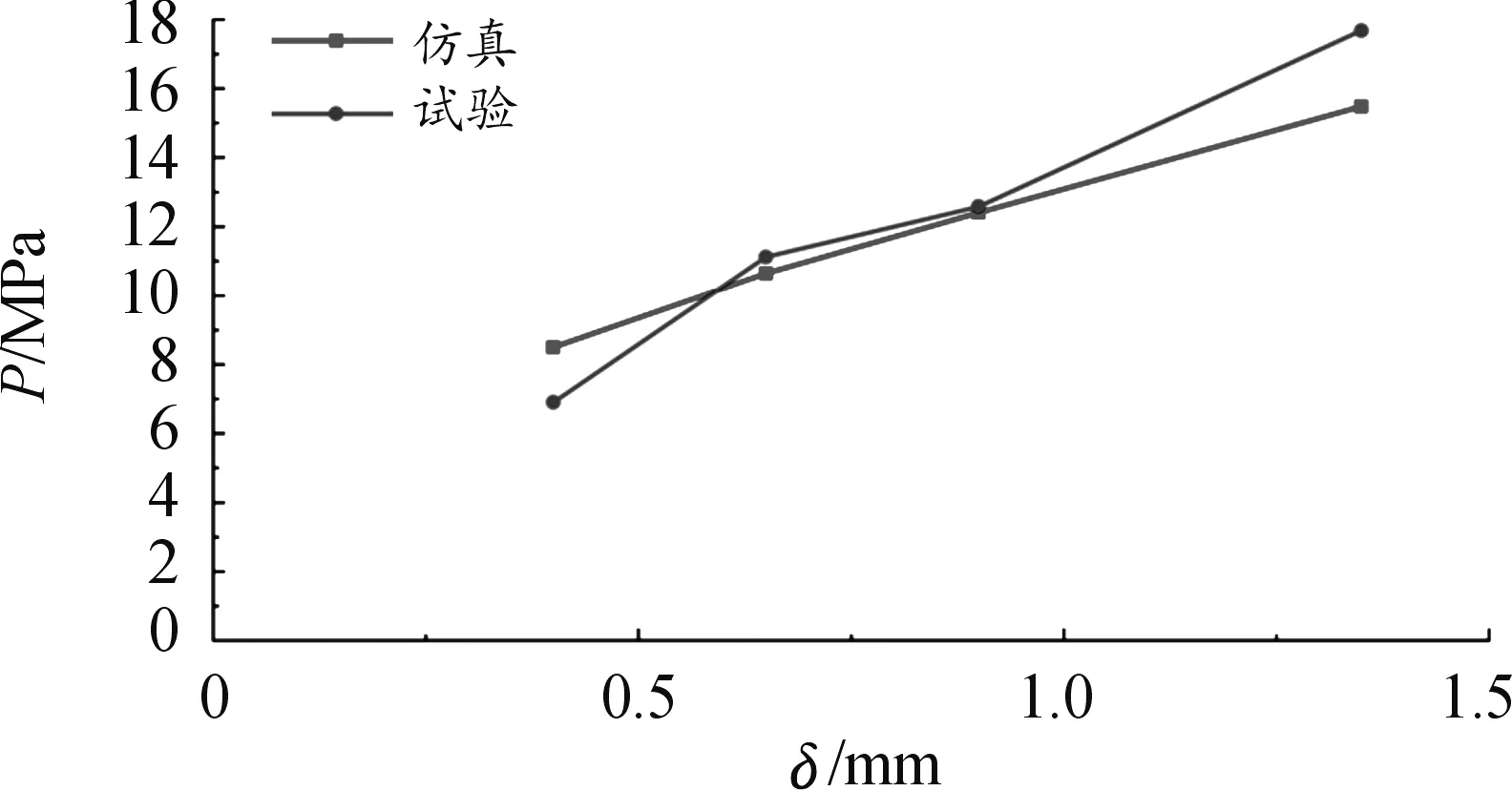
图11 仿真和试验中不同有效厚度的打开压力差曲线

图11中数据为不同有效厚度的堵盖的打开压力差，由图中仿真计算结果可知，在其他情况相同的条件下，堵盖的有效厚度越大，其打开压力越大，且两者数值的变化趋于线性增长。仿真结果与试验得到的平均打开压力有差别，0.4 mm有效厚度时仿真结果大于试验结果，0.65 mm有效厚度和0.9 mm有效厚度时仿真与试验结果十分接近，在1.35 mm有效厚度时差别最大，相差为2.20 MPa，造成这种结果的原因可能是仿真时材料应变率设置与实际有些许偏差。

在单兵筒式武器实弹射击过程中，堵盖打开之后会向后喷出，其喷出时的速度决定它所携带的动能大小，直接影响武器系统后喷危险界限的大小，因此在数值仿真过程中，对它在打开一瞬间的速度进行观测，得到如图12。

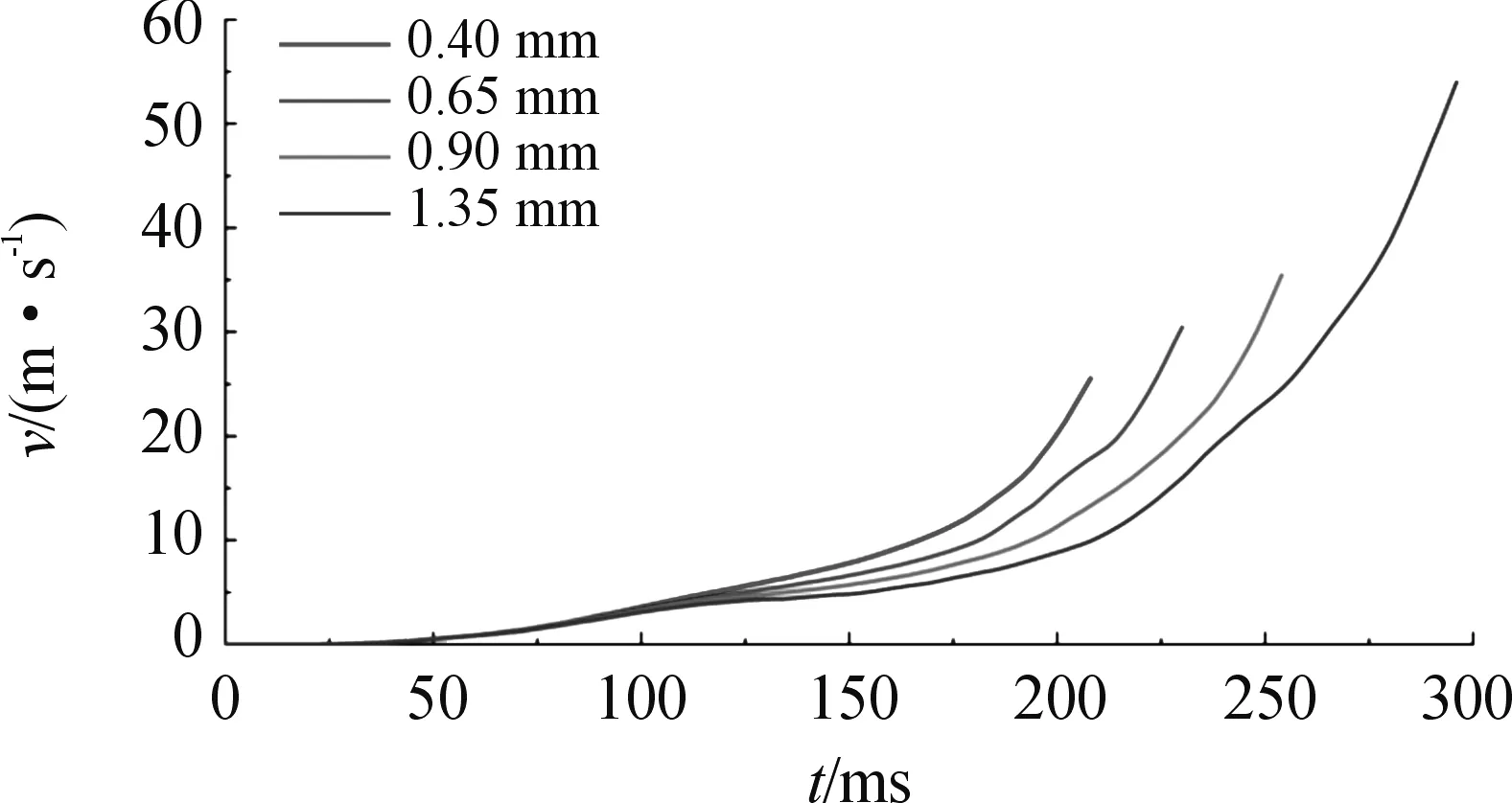
图12 不同有效厚度的堵盖在打开过程中的速度曲线

由图12可知，随着有效厚度变大，速度变化曲线逐渐变缓，其加速度与有效厚度成反比，但有效厚度越小，打开时间越靠前，最终打开时的速度与有效厚度成正比。即使打开时速度最低的有效厚度为0.4 mm的堵盖，其速度也达到了25 m/s以上，所携带动能较大。

4.3 堵盖制造公差对打开压力的影响

2A12铝合金在生产制造过程中，会产生尺寸偏差，本节对考虑公差的2A12铝合金堵盖打开压力进行分析。

2A12铝合金堵盖的打开压力主要受到破坏段尺寸的影响，在考虑公差时可以只考虑破坏段尺寸的公差，破坏段的公差又要从两方面考虑，即厚度方向的公差和宽度方向的公差。以δ代表破坏段的厚度，L代表破坏段的宽度，破坏段的局部如图13所示。

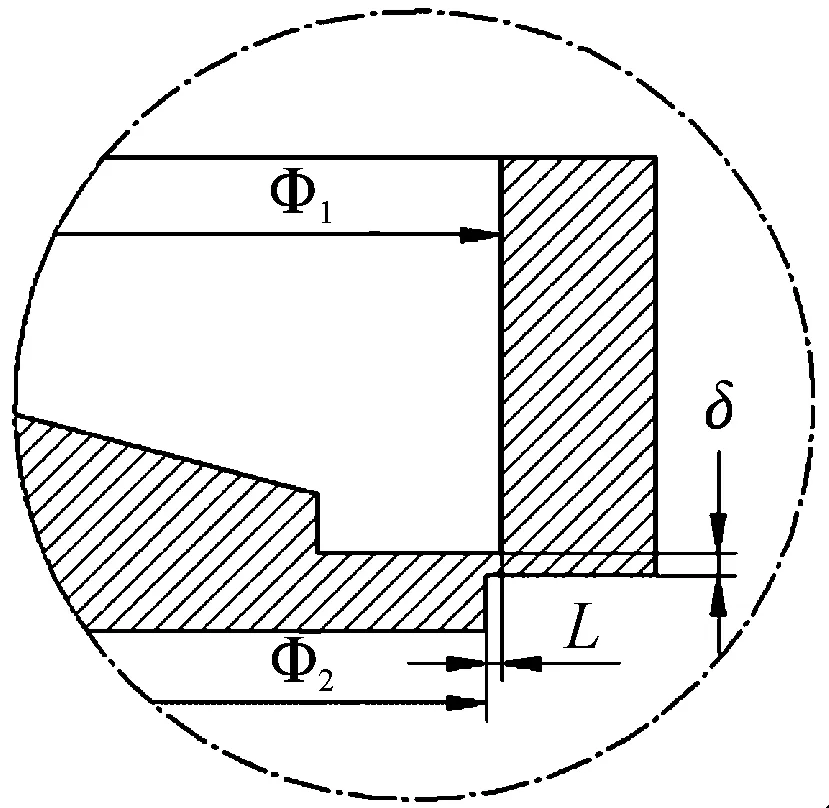
图13 堵盖破坏段局部

图13为图1在破坏段的局部放大图，其宽度L=(Φ1-Φ2)/2，考虑公差存在的情况下，Φ1采用H7级孔公差，为上偏差0.03 mm，Φ2采用h7级轴公差，为下偏差-0.03 mm，δ的公差采用上下偏差±0.01 mm。为保证计算结果的准确性，本节仿真计算涵盖4种有效厚度的2A12铝合金堵盖的宽度和厚度公差，采用定宽度变厚度和定厚度变宽度的方法，增加宽度方向两侧各偏差为0.015 mm的情况，共进行16次计算，除破坏段尺寸外，其他各项设置均与前文相同，最后对各项计算的打开压力进行记录。考虑破坏段公差与不考虑公差情况下的打开压力如图14和图15所示。

图14 考虑厚度公差堵盖打开压力直方图

图15 考虑宽度公差堵盖打开压力直方图

图14为考虑厚度方向的正负公差与不考虑公差情况下的4种有效厚度的2A12铝合金打开压力对比图，由图可知，在厚度方向正负公差为0.01 mm情况下，无论是正公差还是负公差，在与不考虑公差时的堵盖打开压力变化不大，厚度方向的公差对堵盖的打开压力影响较小。

图15为考虑宽度方向的公差与不考虑公差情况下的4种有效厚度的2A12铝合金打开压力对比图，其中L=0.25 mm代表不考虑公差，L=0.265 mm代表偏差是0.015 mm的情况，L=0.28代表公差是0.03 mm的情况。由图可知，宽度方向的公差对打开压力的影响同样不明显，但比厚度方向的公差对打开压力的影响要大，宽度公差会使堵盖打开压力变小。

以上对公差的计算均基于堵盖破坏段在周向上厚度及宽度均匀的情况，由4.1分析结果可知破坏段的厚度对堵盖打开压力影响较大，若破坏段周向公差得不到控制，使得厚度存在差异，则可能造成堵盖打开过程姿态产生偏转，甚至出现堵盖打开不完全的情况。因此，在2A12铝合金堵盖的生产制造过程中，应在厚度、宽度和周向上控制公差的大小。

5 结论

1) 堵盖结构形状设计合理，强度达到使用要求；模拟试验装置满足堵盖试验的要求，能够有效节省试验时间和成本。

2) 堵盖有效厚度增大，打开压力随之增大，且两者数值增长趋近于线性增长，试验与仿真结果较符合；堵盖在打开过程中,如有效厚度越大，打开速度越快；公差对堵盖打开压力存在影响，堵盖制造应考虑控制宽度和厚度公差，尽量减少周向公差，避免堵盖打开过程中姿态不可控。

3) 2A12铝合金堵盖打开压力可通过有效厚度进行控制，且控制精度较高。但因其打开速度较高，易造成较大的后方危险界限，所以在实际使用过程中应考虑场地限制，后续研究将围绕降低其后方危险界限方面展开。