基于虚拟圆球模型的格网SINS/GNSS极区组合导航方法

葛浩冉，徐 祥，黄 玲，赵鹤鸣

(苏州大学电子信息学院，苏州 215006)

0 引言

近年来，北极的战略价值不断提高，受到国际社会的普遍关注。可以预见，越来越多的极地考察任务将实施，极区精确导航将成为支撑极地考察的核心技术之一。惯性导航系统可以全自主地完成导航工作，是极区导航的主要设备。现代导航均以经线作为航向参考基准，使用经纬度来表示位置，而北极附近经线迅速收敛于极点，造成建立相对经线的航向参考基准越来越困难，使得传统的惯性导航系统在极区无法定向。

目前，极区惯性导航的主流解决方案有横向坐标系[1]和格网坐标系[2]导航算法。地球作为导航解算的参照体，其模型的选择是惯性导航系统的重要参数，常采用传统圆球模型和旋转椭球模型对地球作近似描述。在文献[3]中提出了圆球模型下的惯性导航力学编排，计算简单但不可避免地产生原理性误差。在文献[4]中提出了椭球模型下的惯性导航力学编排，可以避免圆球模型带来的原理性误差，但是引入曲率半径的计算，使得导航解算过程复杂化。在文献[5]中提出了虚拟圆球的概念，利用虚拟圆球模型简化导航力学编排，其精度与椭球模型一致。分析惯性导航系统的误差特性是抑制导航误差、提高导航精度的重要步骤，在文献[6-7]中为了简化误差方程推导，均将地球视作圆球模型，以及在文献[8-9]中阻尼技术和文献[10-11]中组合导航系统设计均采用地球圆球模型。对导航系统进行性能评估与验证，实地测试是不可或缺的部分。由于极区实测获取数据难度大，因此获取极区轨迹数据的主要思想是将中低纬度实验数据通过数学方法转换到高纬度地区，目前已有文献中的主要方法包括纬度增量法[12]、坐标系旋转法[13]和姿态速度不变法[14-15]。通过对比分析，姿态速度不变法可以在转换过程中减少轨迹压缩，同时满足极区的地理特性。

针对上述提出的采用圆球模型误差特性进行组合导航系统设计的问题，本文在文献[5]提出的虚拟圆球模型的基础上推导误差方程，设计格网系组合导航系统，实现了捷联惯导地球模型与滤波模型的统一。本文添加了跑车实验，使用文献[14]中的格网姿态速度不变的(Grid Attitude and Velocity Invariant Method，G-AVIM)虚拟极区方法，将低纬度实验数据通过算法转换到极地区域。实验数据结果表明：基于虚拟圆球模型下的格网系捷联惯性导航系统(Strapdown Inertial Navigation System，SINS)/全球卫星导航系统(Global Navigation Satellite Systems，GNSS)组合导航系统可以完成极区导航工作。

1 导航力学编排

采用格网系进行极区惯性导航，推导基于虚拟圆球模型下的导航力学编排。记地球坐标系为e系，载体坐标系为b系，地理坐标系为g系，格网坐标系为G系。

1.1 格网坐标系

设载体的位置为P，格网坐标系的定义如图1所示，以O为球心，地球坐标系记为(xe,ye,ze)，以P点处平行于本初子午面的平面作为格网平面，格网平面与当地切平面的交线定义为格网北向，格网天向与地理天向重合，格网东向在切平面内与格网北向和天向构成右手直角坐标系。格网北向与地理北向之间的夹角σ称为格网方位角。地理坐标系各轴向量记为(E,N,U)，格网坐标系各轴向量记为(GE,GN,GU)。λ和L分别表示P点处的经度和纬度。

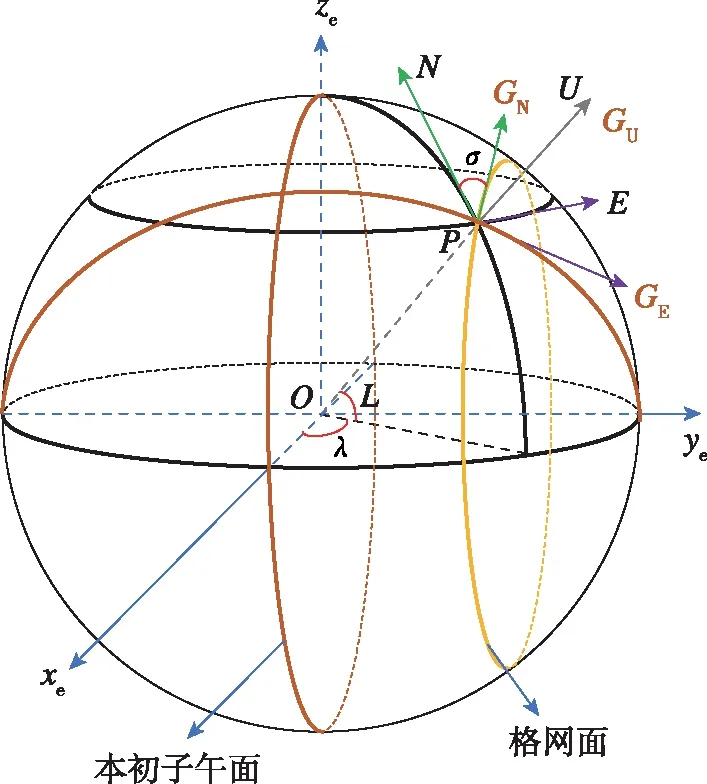
图1 格网坐标系Fig.1 Grid coordinate system

格网坐标系与地理坐标系之间的转换关系为

(1)

对于北半球，格网方位角σ的正弦和余弦可以描述为

(2)

(3)

1.2 惯导力学编排

虚拟圆球模型是以载体所在的卯酉圈半径作为圆球半径人为构造的圆球。在图2中，Re和Rp分别为地球椭球模型的长轴半径和短轴半径；P点的地心纬度和地理纬度分别为Le和L；以O点为圆心，OP为半径所画虚线为虚拟圆球。

图2 虚拟圆球原理图Fig.2 Virtual sphere schematic diagram

设虚拟圆球的半径为Rt，具体的计算过程和符号说明可参见文献[5]

(4)

基于虚拟圆球模型的格网系导航力学编排的姿态方向余弦矩阵、速度和位置微分方程[16]可表述为

(5)

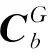
(6)

其中，格网系下的补偿速度为

K为参考椭球变换为虚拟圆球的尺度系数矩阵，k为尺度变换系数，具体符号说明可参见文献[5]

2 导航误差方程

现有文献中，由于椭球模型下的格网系编排复杂，为简化误差推导方程，均近似采用圆球模型。本文将推导基于虚拟圆球模型的格网系误差方程。

地球坐标系和直角坐标系之间的转化关系为

(7)

式中，Rth=Rt+h，h为载体高度；e为椭球第一偏心率。

对式(7)求微分得

δRe=MPR·δP

(8)

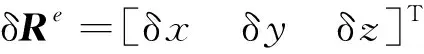
(9)

(10)

式(10)中，Ω为地球自转角速度。

(11)

由式(8)和式(11)可以得到

(12)

(13)

其中

(14)

(15)

式中

由式(8)和式(13)可以得到

(16)

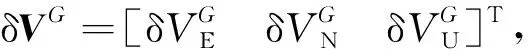
(17)

3 格网系组合导航算法

现有文献在设计组合导航的滤波模型时，为简化计算将地球视作圆球。本文为提高组合导航精度，将捷联惯导机械化的地球模型与滤波模型进行统一，均采用虚拟圆球模型。设计了基于虚拟圆球模型的格网系SINS/GNSS组合导航系统。

3.1 系统状态方程

由误差方程可得系统状态方程为

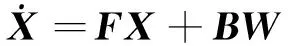
(18)

式中，F为状态转移矩阵；B为系统噪声分布矩阵；W为系统噪声向量。

F=

(19)

(20)

(21)

3.2 系统量测方程

在高纬度地区GNSS可输出ECEF坐标系表示的位置，格网系输出位置也采用ECEF坐标系，因此，组合导航系统选择格网SINS位置与GNSS位置的测量差作为组合导航系统的观测值，建立量测方程为

(22)

则量测方程的矩阵形式为

Z=HX+V

(23)

式中，H为量测矩阵，V为量测噪声。

(24)

其中，I3表示三阶单位矩阵。

4 实验与分析

为验证基于虚拟圆球模型下格网系SINS/GNSS极区组合导航算法的正确性和可行性，传统的纯数学仿真不能反映环境影响和完全模拟载体运动，本文使用文献[14]中的虚拟极区方法，将低纬度跑车实验数据通过G-AVIM算法生成极地地区数据。

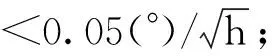
图3 实验车与设备Fig.3 Experiment vehicle and equipment

现场实验在苏州市完成，起始位置为[31.312164°N 120.648157°E 4.5m]，时长2.5h，最大速度约为25m/s。建立极区轨迹，将起始点设置为北极点90°N，转换后的极区经纬度轨迹如图4所示。可以看出，该轨迹在极点附近产生并穿过极点，经度符合实际中极区经度特点。仿真结果如图5～图7所示。

图4 极区轨迹与经纬度图Fig.4 Latitude and longitude map of polar track

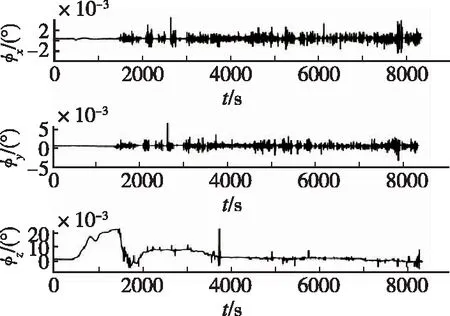
图5 格网系姿态误差Fig.5 Attitude error of grid system

图6 格网系速度误差Fig.6 Velocity error of grid system

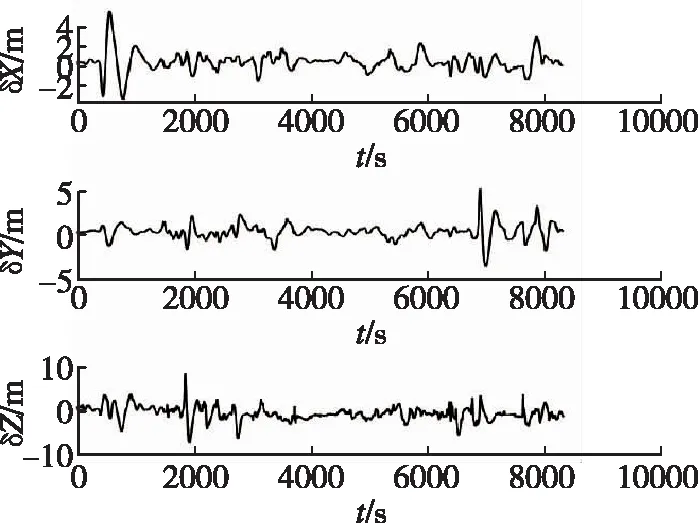
图7 格网系位置误差Fig.7 Position error of grid system

图5～图7所示为基于虚拟圆球模型的组合导航系统误差图，由图5姿态误差可以看出，水平姿态误差角十分平稳，误差基本在0.2′左右小范围波动，最大误差不超过0.3′，由于惯性器件零偏导致航向误差角在前2000s最大误差达到1°，后面随着载体做转弯等机动，使得惯性零偏得到补偿，航行姿态角趋于稳定，误差不超过0.2′；图6速度误差收敛后稳定在0.1m/s，最大误差不超过0.2m/s；图7为ECEF坐标系下的位置误差，水平方向位置误差不超过5m，垂直方向误差不超过10m。从实验结果分析可知，首先，基于虚拟圆球模型的格网系惯性导航算法可以完成极区的导航任务，在穿过极点与极点附近时都不会发生跳变现象，克服了传统中低纬度惯导的缺陷，验证了本文方法的可行性；其次，组合导航系统的定位误差不超过5m，可以满足极区航行的精度要求。

5 总结

本文针对格网系组合导航系统模型不统一的问题，提出了一种基于虚拟圆球模型下的格网系组合导航系统，算法分析与实验结果表明：

1)虚拟圆球模型下的格网系力学编排通过对速度的补偿，弥补了圆球模型下存在的原理性误差，简化了椭球模型的计算复杂度，因此可以简化系统误差方程的推导。

2) 将捷联惯导地球模型与滤波模型进行统一，均采用虚拟圆球模型，不再是椭球模型的惯导更新算法与圆球模型的滤波算法，使得状态转移矩阵更准确，同时统一的模型还可以简化系统设计。

3)本文不再使用纯数学仿真，而是进行跑车实验，利用虚拟极区的方法将轨迹数据转换到极区，验证了实验的有效性和可行性，更具有说服力。