信号交叉口可靠度建模
马志芳 蒋亚丽
(1.兰州交通大学 兰州 730000;2.甘肃建投土木工程建设集团有限责任公司 兰州 730000)
1 研究背景
随着我国经济的快速发展,城市交通出行的负担日益加重,如何缓解交通拥堵,节省出行时间,是目前研究的重点。在此背景下,以交通系统可靠性作为评价车辆通行能力指标的方法被广泛提出。交通系统可靠性的研究始于20世纪80年代,最早是通过网络的拓扑结构分析路网连接可靠度,例如连通可靠度、通行能力可靠度、行程时间可靠度和服务水平可靠度等[1],通常用于分析道路设施及交通流运行状态,但忽略了路网中交叉口对路网可靠性研究的重要性。
在优化交叉口的信号控制指标时,一般认为车辆到达率是服从一定概率分布[2],目前学者多通过可靠性指标来评价其性能的稳健性或基于此设计优化信号配时方案。为评价该交叉口运行的稳定性,优化信号配时方案,于泉等[3]定义了固定配时方案下的控制方案可靠度,分析高峰时间段的车流量,依据可靠度来确定相应的高峰时段配时方案的启动时间。吕斌等[4,5]采用相位清空可靠度作为评价指标,依据信号交叉口车辆随机到达的特点,研究了相位清空可靠度与周期时长、绿灯时间之间的关系,并通过Gauss消元法得到当车辆到达交叉口服从正态分布和负指数分布时,相位清空可靠度的计算公式。刘刚等[6]基于服务水平的交叉口可靠性模型,在考虑车辆到达随机性的基础上,把服务水平可靠度作为信号控制交叉口可靠性指标,研究其与车辆到达可靠性的关系,建立信号配时模型。郑慧敏[7]借助实际测量数据,对车辆到达率进行分析,提出了服务水平可靠度和排队长度可靠度指标,研究在不同可靠度指标下的不同分布模型、可靠度需求以及到达车辆波动程度对信号配时的影响。在此基础上,将排队长度可靠性引入干线交叉口,建立以干线排队长度可靠性最大为目标的相位差优化模型,为本文日后研究的提供方向。陈晓明等[8]定义了通行能力可靠度,给出了车辆随机到达条件下通行能力可靠度的估计方法。同时考虑在混合交通情况下,影响通行能力的因素,采用VISSIM软件建立仿真模拟。
上述研究中,在考虑车流随机性的分布中,大多采用假定车辆到达服从某种分布,缺少验证及一定的普及性。在考虑不同可靠度指标中,仅研究单一可靠度与车辆随机到达和周期时长之间的关系,建立的交叉口可靠性指标模型较为简单。且现有的研究多停留于表面框架和概念,应用于交通管理实践研究的成果较少。本文根据相位清空可靠度的定义,结合车辆随机到达特性分析,定义了车道可靠度、相位可靠度,通过其串并联关系,推导出交叉口可靠度模型并进行仿真。同时将交叉口可靠度作为评价指标,对文中假设的三种信号配时方案,从不同角度进行评价,选取最优的信号配时方案。
2 交叉口可靠度模型
2.1 相位清空可靠度定义
相位清空可靠度定义[9]:假设该信号交叉口有n个相位,相位i(1,2…n)的绿灯时间能够放行所有本周期内到达机动车的概率,用Pi表示相位清空可靠度,则:
Pi=Pr(qijC≤giSij)
(2.1-1)
式中,Sij表示第i个相位对应的第j条车道的饱和流量,单位pcu/h;qij表示第i个相位对应的第j条车道的车辆到达率,单位pcu/h;C表示该交叉口周期时长,单位s;gi表示第i个相位的有效绿灯时间,单位s。
由上式(2.1-1)得知,各相位的车流状态可以通过相位清空可靠度的大小来体现,可用于评价各相位信号配时参数是否满足交通需要的能力,故综合计算分析交叉口可靠度的大小可利用相位清空可靠度指标。
基于相位清空可靠性的交叉口可靠度模型
假设交叉口信号相位方案是由n个相位以一定顺序排列组合而成,本文称其组合方式为串联,即任一相位失效将引发该交叉口车辆拥堵,造成交通瘫痪。且该串联系统的失效率为所有组成相位的失效率之和。而第i(i=1,2,3…n)个相位由m条车道以一定顺序排列组合,本文假设车道之间相互独立,其组合方式为并联。即当m条车道都失效时,该相位才失效,进而整个交叉口出现交通拥堵。
由上述交叉口可靠度模型可得交叉口串—并联系统图,如图1。
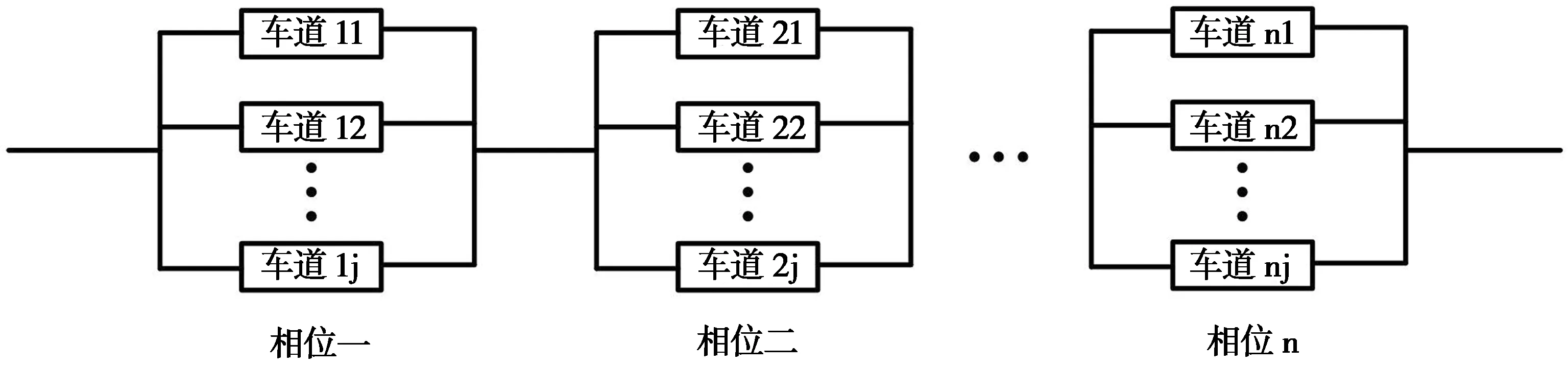
图1 交叉口串—并联系统图
交叉口的可靠度R为:
R=P{min{P1,P2,P3…Pn}≥0}
=P{P1≥0,P2≥0…Pn≥0}
(1)
式中,n表示该交叉口信号配时方案包含的相位数。
第i个相位的可靠度Pi为:
Pi=P{max{Li1,Li2,Li3…Lij}≥0}
=1-P{max{Li1,Li2,Li3…Lij}<0}
=1-P{Li1<0,Li2<0…Lij<0}
(2)
第i个相位对应的车道可靠度Lij为:
Lij=Pr(qijC≤giSij)
(3)
将式(2)、(3)带入式(1)得到交叉口可靠度表达式如下:
(4)
根据上式(4)可知,对于某个给定信号配时方案的交叉口,其交叉口可靠度仅与车辆到达率qij和饱和流量Sij有关,现有研究认为车辆的到达率与车道的饱和流量互不影响[7,8],因此本文假定车道的饱和流量在研究时间段内为常数。由于车辆到达具有随机性,因此交叉口可靠度会随车辆到达率的变化而变化。若已知该交叉口的信号配时方案,各车道机动车的到达率qij和饱和流量Sij,可利用式(4)求得该交叉口的可靠度,定量的评价该交叉口运行状态,为优化交叉口信号配时方案提供依据。反之若要使交叉口满足一定的可靠度指标,使得道路通行更加合理、有效、便捷,也可利用式(4)求得满足一定交叉口可靠度需求的信号配时方案。
因此,定义交叉口可靠度,评价交叉口信号配时方案的模型为:
(5)
由于信号相位i对应的进口道车辆到达率qij具有随机性。若假设qij的概率分布已知,则根据公式(3)可以建立相位i有效绿灯时间gi与车道可靠度Lij之间的关系,即Sij,Lij已知,再根据信号配时约束条件可以获得该交叉口信号周期及各相位绿灯时间的计算公式。下面将针对进口道车辆到达率服从标准正态分布时,对信号配时计算公式进行研究。

(6)
于是可以得到

(7)
式中:
φ-1(Lij):标准函正态分布函数φ(Lij)的反函数。
基于周期时长与绿灯时间之间的关系式:
(8)
式中:L为总损失时间。
相位i的绿灯时间可以通过计算得到:

(9)
将上式(7)(8)(9)带入上式(5)得到交叉口可靠度模型为:
(10)
该模型一方面可根据己知交叉口信号控制方案、各相位机动车到达率qij和饱和流率Sij,求解现有控制方案下交叉口可靠度,为评价和调整优化信号配时参数、交通组织方案提供依据。另一方面,可以根据到达车流的分布及配时约束确定满足一定交叉口可靠度的信号配时方案。
此外,在验证交叉口可靠度的准确性上,本文根据计算的平均信号控制延误来确定,其计算公式如下:
(1)各车道延误公式:
d=d1+d2
(11)

(12)

(13)
式中:
d1:均匀延误,即车辆均匀到达所产生的延误,s/pcu;
d2:随机附加延误,即车辆随机到达并引起超饱和周期所产生的附加延误,s/pcu;
x:所计算车道的饱和度;
CAP:所计算车道的通行能力, pcu/h;
T:分析时段的持续时长,h,取0.25h;
e:单个交叉口信号控制类型校正系数,定时信号取e=0.5;
(2)各进口道的平均信控延误,按该进口道中各车道延误的加权平均数估算。
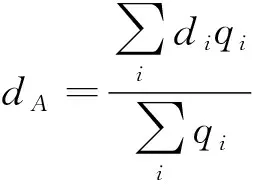
(14)
式中:
dA:进口道A的平均信控延误,s/pcu;
di:进口道A中第i车道的平均信控延误,s/pcu;
(3)整个交叉口的平均信控延误,按交叉口中各进口道延误的加权数估算。

(15)
式中:
dI:交叉口每车的平均信控延误,s/pcu;
qA:进口道A的高峰15min交通流率,辆/15min。
3 算例分析
3.1 影响参数分析
为证明交叉口可靠度与车辆期望和方差的关系,本文假定交叉口各条车道段宽度为3.5m,各进口均设置为单向3车道,分别为直行、左转、右转车道。交叉口的渠化方案和相位方案如图2所示。
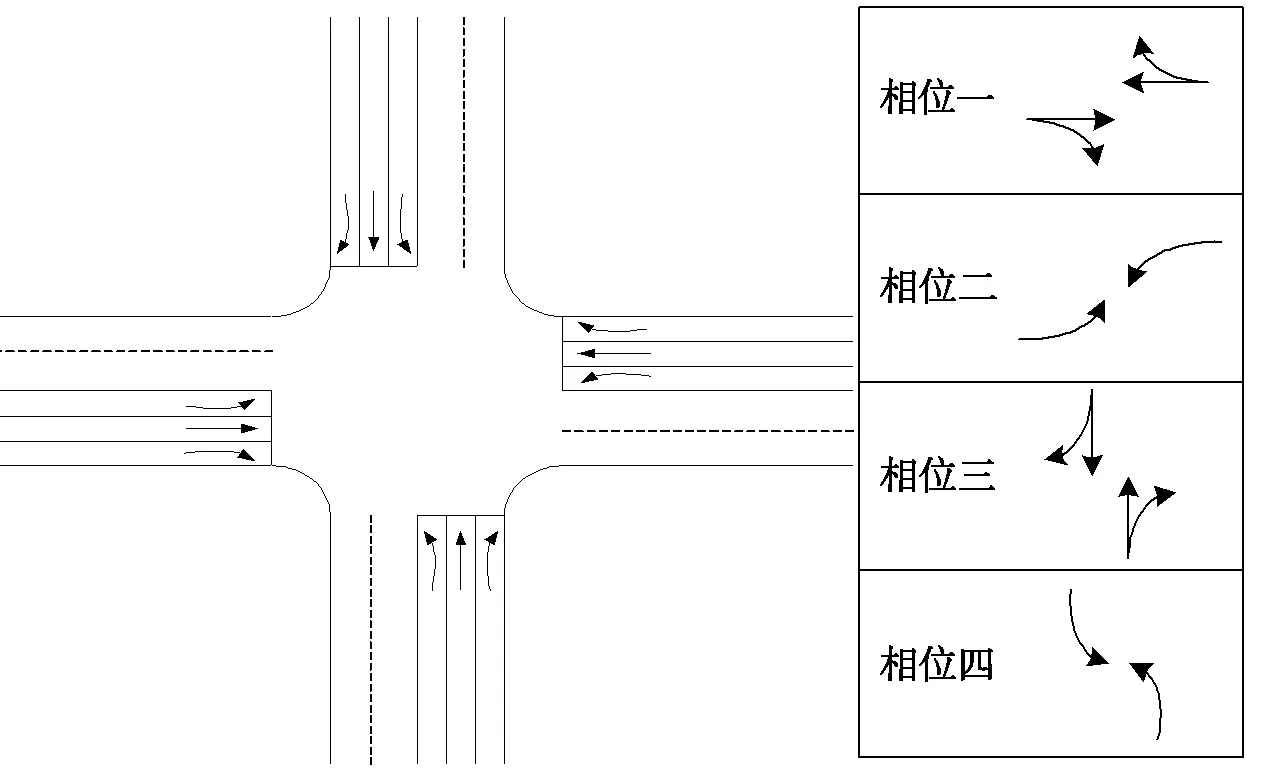
图2 仿真交叉口渠化及信号相位相序图
在算例分析过程中,为了控制单一变量,使得计算过程中绿灯时间改变仅与东进口直行车道车辆到达率的变化有关。现假定东进口直行车道车辆到达率服从正态分布,期望为250-450pcu/h,步长为50pcu/h,方差为0-100,步长为10pcu/h,其余各进口道车辆到达率服从均匀分布。各方向进口道的饱和流量、期望和方差如表1所示。周期损失时间L=8s。

表1 交叉口各进口道的饱和流量、期望和方差
本次研究采用Webster周期公式计算交叉口周期时长,Matlab作为仿真工具,求解交叉口可靠度。改变交叉口东进口道车辆到达的期望和方差,得到周期时长和交叉口可靠度的仿真结果并进行分析。

图3 交叉口东进口直行车道车辆到达期望与可靠度关系图 图4 东进口直行车道车辆到达期望与周期时长的关系图
由图3可知,当东进口直行车道车辆到达率增加时,东进口车道可靠度呈单调递减趋势,由1降至0.005。由图4可知,当东进口直行车道车辆到达率增加时,交叉口的周期时长随之增加,由56s增至166s,其对应的相位一的绿灯时间从15.4s增加到97.8s。
由图3可知,在东进口直行车道车辆到达期望值变化过程中,交叉口可靠度始终稳定在0.6-0.8之间,无较大波动。结合图4可知,为保证交叉口可靠度在0.6~0.8之间,周期时长也需要随之增加,且甚至达到166s,超出了限定的交叉口最大周期时长,进而证明车辆随机到达特性对交叉口信号设置参数的影响显著。

图5 在不同期望、不同方差条件下的交叉口可靠度
本文交叉口的渠化方案中,各方向直行车道仅有一条,则主要分析该交叉口东进口直行车道车辆到达率的期望为250-450pcu/h,方差为0~100条件下,交叉口可靠度的变化情况。由图5可知,当该交叉口东进口直行车道车辆到达率的期望、方差发生变化时,交叉口可靠度也随之变化。当交叉口东进口道车辆到达率期望一定时,交叉口的可靠度随方差的变化,上下浮动。由图可知,方差在0~10范围内变化时,该车道的车辆数变化幅度较低,信号周期满足交叉口车辆通行需求,因此各期望条件下交叉口可靠度基本保持定值;方差在10~55范围内变化时,随车道车辆数变化幅度的增加,此时该车道接近饱和状态,交叉口可靠度的波动程度相较0~10范围内增大;方差在55~100范围内变化时,车辆到达不稳定性增加,易发生排队拥挤现象,故波动性较为明显。此外当交叉口东进口直行车道车辆到达率方差一定时,随着期望的增加,交叉口可靠度降低。

图6 不同期望、方差条件下的车辆延误
由图6可知,方差在0~20范围内变化时,东进口直行车道车辆延误保持稳定;方差在20-30范围内变化时,东进口直行车道车辆延误有所增加;方差大于70时,该交叉口易发生排队拥挤情况,东进口直行车道车辆延误稳定性也随之下降,对应交叉口可靠度变化较为明显。当期望为450pcu/h,方差为70时,延误出现极大值;当期望400pcu/h,方差为90时,出现极小值,易引发车辆二次排队,造成不同程度的交通拥堵,结合可靠度分析具有一定的不适用性。由图5和图6可知,当该交叉口东进口直行车道车辆的期望为250pcu/h,方差为65时,车辆延误为15.98s/pcu,交叉口可靠度为0.569,且此时交叉口可靠度最高。综上所述,交叉口交通流的随机特性对交叉口可靠度影响显著,进而对交叉口信号配时参数设计影响显著,因此在设计交叉口信号配时方案中应当充分考虑车辆到达到随机性的因素。
3.2 交叉口可靠度评价分析
为证明交叉口可靠度可作为交叉口信号配时方案的评价指标之一,现改变该交叉口的信号配时方案,求解不同信号配时方案下的交叉口可靠度,结合交叉口车辆延误,选出适合该交叉口的信号配时方案。本算例沿用算例1交叉口渠化方式,在同种交通到达率条件下设计三种信号配时方案。方案一沿用算例1的四相位相位方案[10]。
方案二、方案三采用的相位方案分别如图7(a),(b)所示。

(a) (b)
假设该交叉口各进口道车辆到达率服从均匀分布,其中东进口直行期望为350,方差为0,其他各方向进口道的饱和流量、期望和方差如表1所示。
此外,为分析交叉口可靠度对信号配时方案评价的准确性,假定信号周期为68s,周期总损失时间L=8s,同时借用整个交叉口的每车平均延误作为其验证指标,交叉口每车平均延误公式见公式2.2-15。对三种信号配时方案及其可靠度、车辆延误进行仿真计算,计算结果见表2。
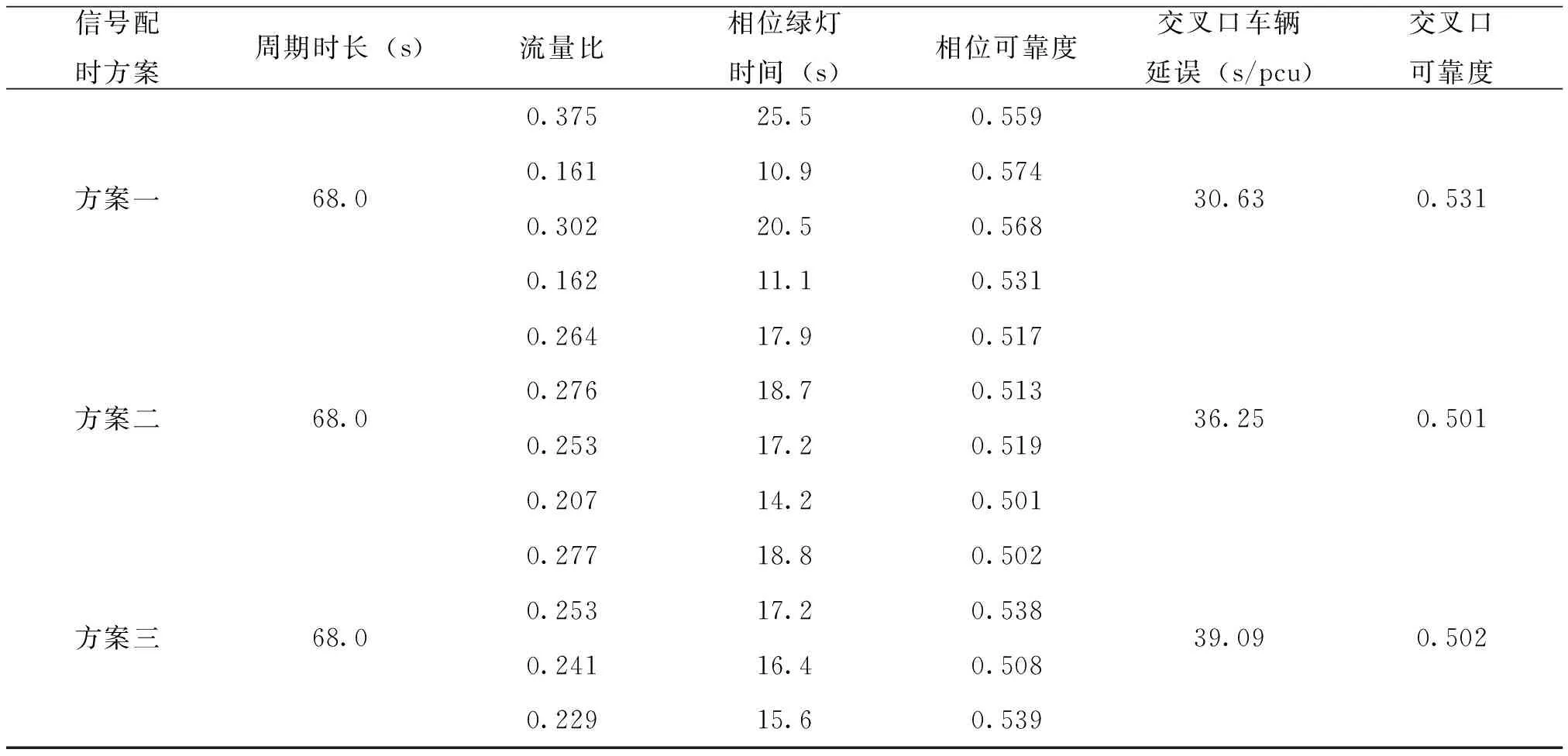
表2 交叉口信号配时方案及对应的可靠度
由表2可知,在交叉口信号配时方案中,方案一与方案二比较,当信号周期一定时,方案二各相位绿灯时间较为均衡,一定程度上限制了交叉口各方向直行车道的通行能力,使得车流量较大的车道出现二次排队情况,因此相较于方案一,方案二的交叉口可靠度降低,交叉口车辆延误增加。方案一与方案三比较,区别在于方案一右转与直行同时放行,方案三右转与左转同时放行。方案变化后,直行车道放行时间减少,左转和右转放行时间增加,在一定程度上造成直行车道的二次排队,左转车道的绿灯损失时间较长。因此方案三的交叉口可靠度较方案一有所降低,交叉口车辆延误增加。故在本文假设的三个信号配时方案中,方案一最佳,交叉口可靠度为0.531,交叉口车辆延误为25.63 s/pcu。
综上所述,在交叉口信号配时方案中,结合交叉口车辆延误可知,相位相序对交叉口可靠度也具有一定的影响。因此为使车流在交叉口的运行状态满足一定的可靠度需求,应在信号配时设计中充分考虑相位和相序的影响。
3.3 交叉口可靠度约束分析
为证明交叉口可靠度可作为计算交叉口信号周期的约束条件之一,现将上述模型中式(10)改为:
mind=d1+d2
(16)
式中:
λ:对应相位绿信比;
θ:进口道的饱和度;
R0:满足一定要求的交叉口可靠度。
本算例沿用算例二求得的相对最优相位方案,在保证车辆到达率服从均匀分布的情况下,将满足一定要求的交叉口可靠度作为约束条件,比选方案二中假定R0≥0.70,比选方案三中假定R0≥0.80,结合车辆延误,对该交叉口的信号周期进行调整,算例结果见下表3。
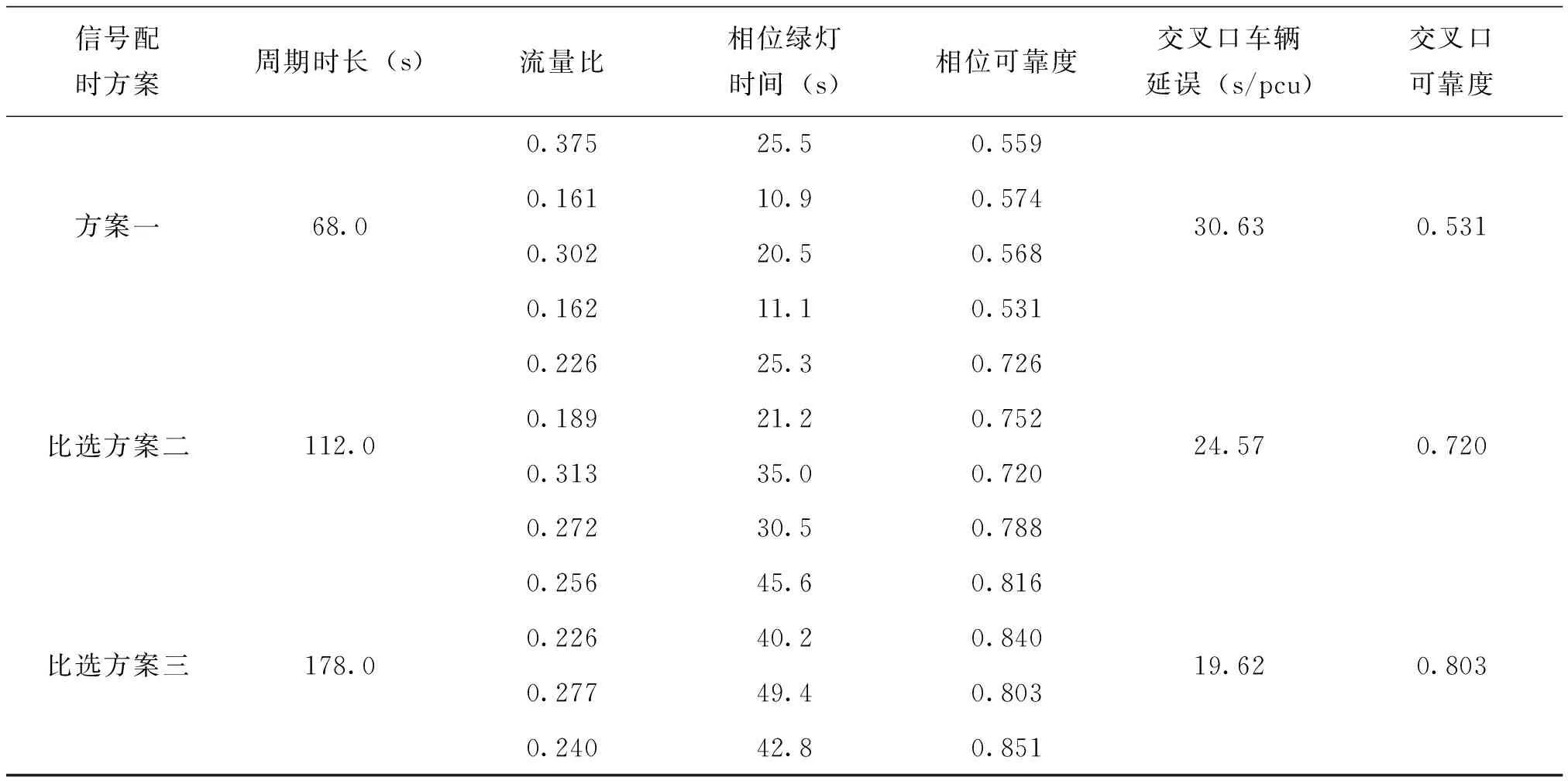
表3 交叉口信号配时方案比较
由上表3可得,在交叉口的车辆到达率服从均匀分布时,保持交叉口的渠化方案和相位方案不变,当交叉口可靠度满足R0≥0.70的条件时,该交叉口的信号配时方案如比选方案二所示,周期时长为112s,交叉口车辆延误为19.53s/pcu。当交叉口可靠度满足R0≥0.80的条件时,该交叉口的信号配时方案如比选方案三所示,周期时长为178s,交叉口车辆延误为16.62 s/pcu,但此时信号周期较长,不满足实际要求。故在本文假设的三个交叉口可靠度中,比选方案二最佳,交叉口可靠度为0.720,交叉口车辆延误为19.53 s/pcu。
综上所述,在交叉口信号配时方案中,结合交叉口车辆延误可知,交叉口可靠度对信号周期时长具有一定的影响,当交叉口可靠度增加时,周期时长也相应增加。因此,在今后计算交叉口信号配时的研究中,可将交叉口可靠度作为其约束条件,优化交叉口信号配时方案。
4 总结
为了评价和优化交叉口的运行状态,判断交叉口信号配时方案是否满足通行需求,本文定义了交叉口可靠度的概念,引入交叉口可靠度的计算公式和评价标准。参考Webster模型,计算交叉口信号配时方案,根据交叉口交通流到达率的随机性特点,对该交叉口在当前信号配时方案条件下的可靠度进行计算,得到了交叉口可靠度与周期时长、车辆到达期望和方差的关系。研究结果表明,当交叉口进口道车辆到达率期望一定时,方差越大,交叉口稳定性越低。当交叉口进口道车辆到达率方差一定时,期望越大,可靠度越低。同时,本文算例二中假设了三种交叉口信号配时方案,将交叉口可靠度作为评价标准,结合车辆延误,证明相位相序对交叉口可靠度具有一定的影响。本文算例三中假设了三种交叉口可靠度值,将交叉口可靠度作为约束条件,结合车辆延误,证明交叉口可靠度对信号周期时长具有一定的影响。因此为使车流在交叉口的运行状态满足一定的可靠度需求,不仅要考虑车辆随机到达的特点,也要考虑在信号配时设计中相位、相序和周期时长的影响。本文研究的交叉口可靠度模型适用于渠化方案较为简单的交叉口,对于含有搭接相位的交叉口信号配时方案不适用,还有待进一步研究。

