一种逐周期条纹背景自适应去除算法
刘 洋,潘 娅,罗玉琴
(西南科技大学 计算机科学与技术学院,四川 绵阳 621010)
0 引言
结构光三维测量技术是一种有用的光学测量技术,其具有设备简单以及在非接触模式下可提供高分辨率的全场测量能力[1]。随着科学技术的飞速发展,结构光三维测量技术在三维重建、位移测量、以及三维形貌测量等诸多领域得到了广泛的研究和应用[2]。这使得结构光测量技术必须具备有效适应不同场景的能力,这对该技术的测量速度和测量精度是一种更高的要求[3]。在保证测量速度的同时如何提高测量精度是研究人员广泛研究的问题。由于相位携带着需要测量的物理量信息,准确的相位提取对于结构光技术的成功应用至关重要。一般情况下,相位提取方法可分为两类[4]:一类是基于单模式条纹图[5],另一类是基于相移技术多模式条纹图[6-8]。基于相移技术的方法往往需要至少三幅模式图,这显然很难达到快速测量的效果。基于单模式条纹的方法以傅里叶轮廓术为代表,将正弦光栅或朗奇光栅投影到被测物体表面上,投影光栅图样的相位受物体的空间轮廓调制。这种相位调制被编码到光栅图形的基本频谱中。采集记录形变光栅图形,利用傅里叶变换从基频谱中提取相位信息,然后根据获得的相位信息重建三维物体表面轮廓。然而变形光栅图像除了基频成分外,还可能包含背景分量和高阶频谱成分。当基频谱较宽时,基频可能被其他频谱所破坏。这就是传统FTP的固有缺点[9-13]。目前为止针对FTP这个缺点已经提出了几种解决方案,周灿林[14]等人提出了一种利用相移去除背景分量的方法。这种方法虽然能有效提高测量精度但是不适合快速测量场景,因为该方法需要至少两幅变形光栅图。利用二维小波变换对背景分量进行抑制也陆续被提出。基于小波的多分辨率特性[15],需要由具有带通滤波器响应的唯一函数通过平移、膨胀和旋转生成一组小波滤波器。当变形光栅图像的带宽较宽时,基频的精确提取就成了频域处理的一个主要问题[16]。文献[17]等人提出了一种基于损失函数最小化的小波变换方法,通过对理想调频信号的分析得到一个恒等式,根据这个恒等式确定一个损失函数,以这个损失函数为标准来选择小波函数。该方法受误差影响易收敛到局部最优解从而影响重建精度,而且计算量较大。同样是基于最优化的思想,文献[18]提出了最小二乘法估计的条纹归一化算法和基于傅里叶变换的条纹归一化算法,这两种算法等于是间接达到了滤波的效果。但是面对不稳定的背景噪声误差较大。文献[19]把π相移的图片编码进彩色图像的不同通道里,达到了单幅投影图的效果,但是彩色图片各通道之间存在通道串扰与不平衡对重建精度影响很大。经验模态分解是一种有效的去除背景分量的方法[20-23],经验模态分解(EMD)将变形条纹分解为由高频到低频的固有模态函数,然后从频谱中分离背景分量。该方法对于一些受噪声干扰或者较复杂的面型重建精度不理想。
目前去除投影条纹图背景分量的方法在条纹图背景分量不均匀时存在去除效果差,严重影响重建精度的问题。本文在实验中发现背景分量不均匀的投影条纹图在单个条纹周期内的背景分量变化很小,可以近似作为常量处理。结合两次希尔伯特变换能有效去除信号直流分量且保持相位信息稳定的特性,提出一种自适应的分周期条纹背景滤除方法。该方法可以很好的消除条纹图中的背景分量,提高FTP(傅里叶轮廓术)的测量精度。通过理论分析,并通过计算机仿真实验与实际测量实验验证了文中方法的有效性。
本文内容安排如下:第一节介绍条纹图周期内背景常量化的分析;第二节介绍所提方法的基本原理;第三节阐述整体算法设计流程。第四节是对周期希尔伯特变换方法和EMD方法进行了仿真与实验对比分析。第五节给出了结论。
1 逐周期背景常量化分析
投影条纹背景分量容易受环境光的干扰,在条纹图的不同区域呈现不同的强度。图1(a)是受环境光干扰的投影条纹图。图1(b)是暗室环境中拍摄的投影条纹图。图2(a)和图2(b)分别是图1(a)和图1(b)行像素强度值分布。图2中的绿色折线表示逐个周期内背景分量的变化,可以看出图1(a)由于受环境光影响背景分量呈现不均匀的分布。图1(b)的背景分量相对稳定。另外本实验在不同环境光照下采集多张投影条纹图,对其背景分量强度变化进行分析。每张条纹图等行间距取10组行数据,计算每组数组整体背景强度变化幅度和该组数据所有周期内背景强度变化的均值。实验环境中分别加入自然光,室内灯光,近距离点光源。实验结果如图3所示。所有实验条纹图整体背景分量变化量均值为18.764 2,单个周期内的背景分量变化量均值为0.655 8。横坐标表示实验组数,0~50组是在暗室环境下的实验数据,50~150组是不同自然光环境中的实验数据,150~200组实验加入室内照明,200~230组实验加入了近距点光源照明。纵轴表示投影条纹图背景分量变化幅度。图中显示随着环境光干扰增加,条纹图整体背景分量不均匀性变大。而同周期区域内的背景分量不均匀性依然很小。根据实验所得数据本题可近似纹图的背景分量在同周期内均匀,大小设为常数如公式(9)。

图1 投影条纹图

图2 行像素强度值分布
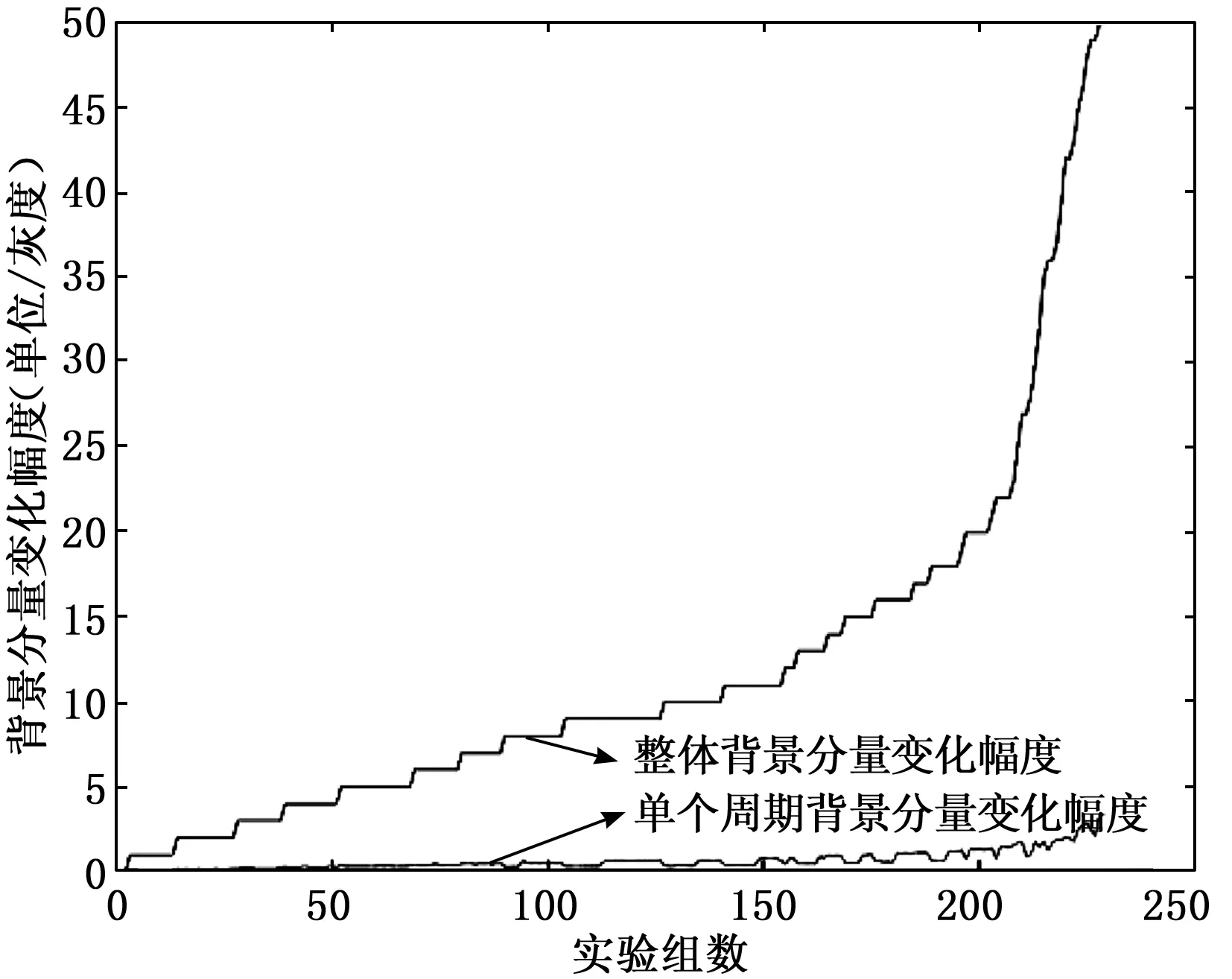
图3 背景分量实验分析图
2 两次希尔伯特变换自适应去除背景分量
信号f(x)的一维希尔伯特变换如下所示:
(1)
表示卷积操作,H表示希尔伯特变换。H(f(x))的傅里叶频谱表示为:
τ[H(f(x))]=-jsgn(w)F(w)
(2)
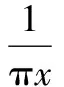
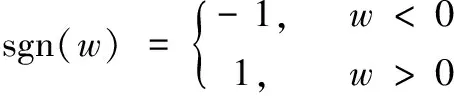
(3)
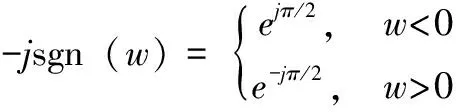
(4)
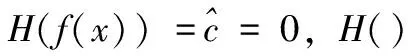
(5)
(6)
根据希尔伯特变换的线性性质可得下式。
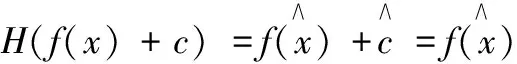
(7)
公式(7)表明希尔伯特变换能自动消除任意常数c。据此,若对投影条纹图进行两次希尔伯特变换,则能自适应地消除投影条纹图背景分量;同时,又保持了原相位的稳定。为了验证结论,论文对模拟条纹进行两次希尔伯特变换。在图4中可以看到变换后信号的背景分量被有效的去除。
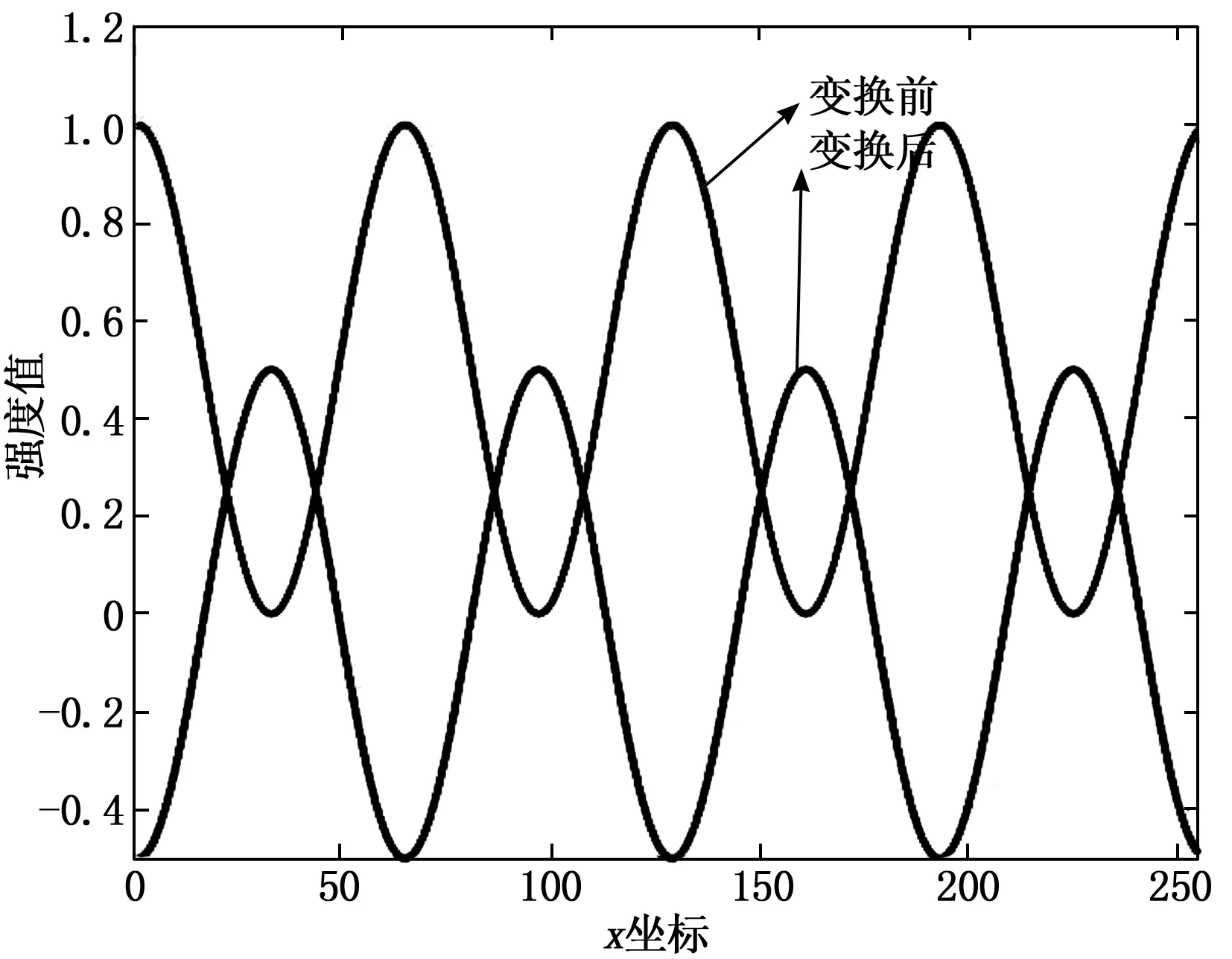
图4 两次希尔伯特变换结果
3 算法设计
投影条纹图的像素点强度值可以用下式表示:
I(p)=a+b(p)cos[φp+2πf*p]
(8)
*表示内积运算,p(x,y)是空域坐标,a(p)和b(p)是背景强度和调制强度。φ(p)是待测的相位分布,f是f(fx,fy)的简写表示频率载波。根据本文第一部分对投影条纹图逐周期背景常量化的分析,可以近似a(x,y)在同一个周期内是常数。于是像素点强度表达式可以表示为:
Ii(p)=ai+b(p)cos[φip+2πf*p]
(9)
i=1,2,...n。p表示像素点坐标(x,y),i表示周期数。ai表示在一个周期内的背景分量。φip表示调制相位。如图5是逐周期希尔伯特变换方法的流程图。用该方法去除条纹背景分量后,再采用FTP方法获得三维重建所需的相位信息,实验表明该方法能有效减少投影条纹背景分量对相位信息的干扰,能提高测量精度。
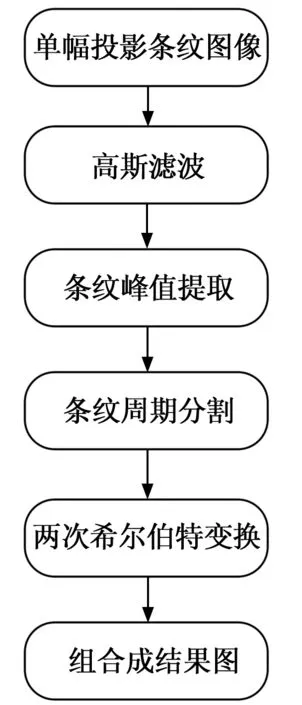
图5 逐周期希尔伯特变换算法流程图
4 实验验证
4.1 仿真实验
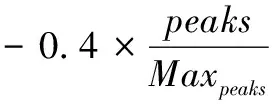
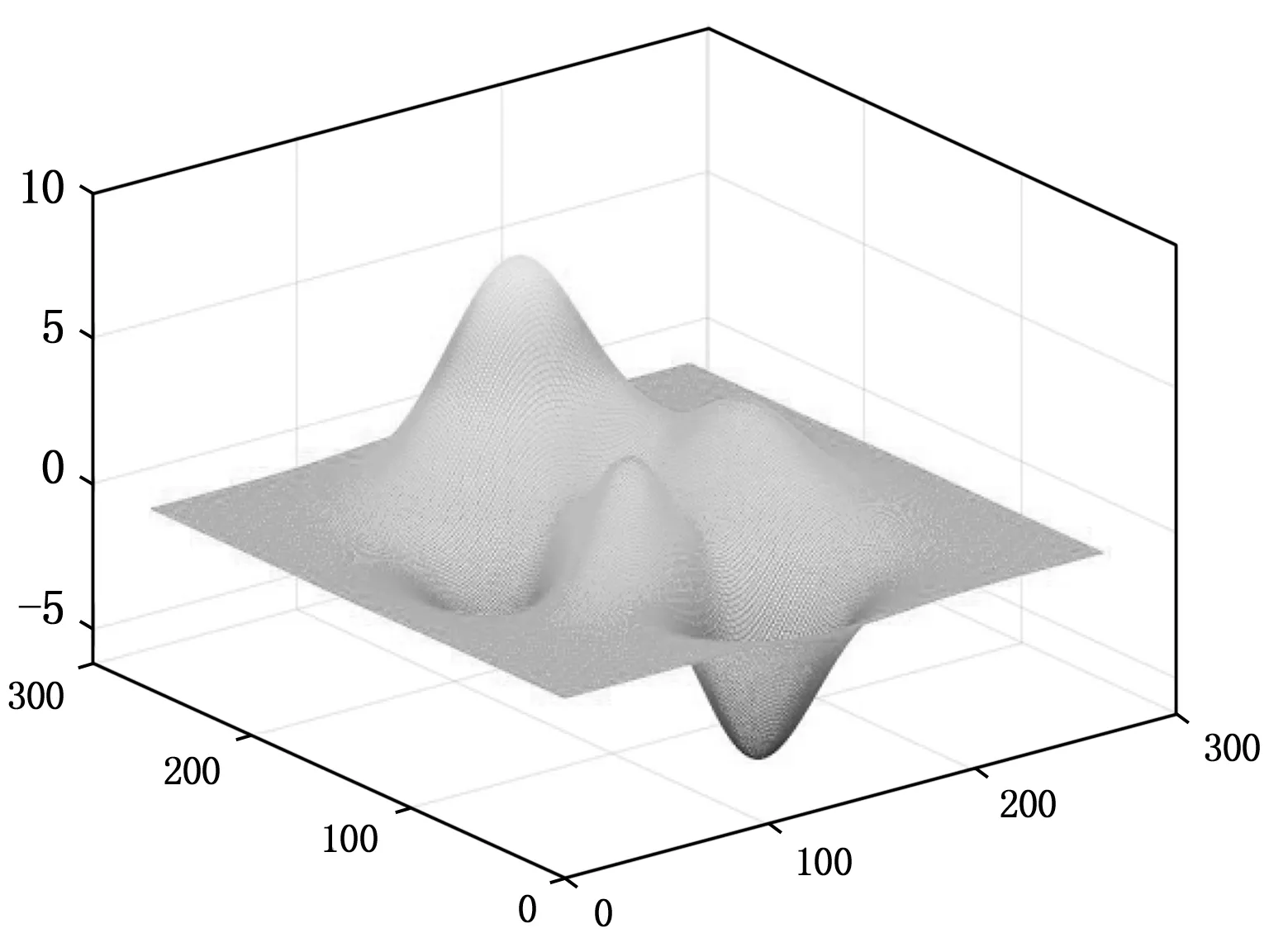
图6 模拟目标三维示图

图7 条纹图

图8 目标条纹图红线标记行强度分布
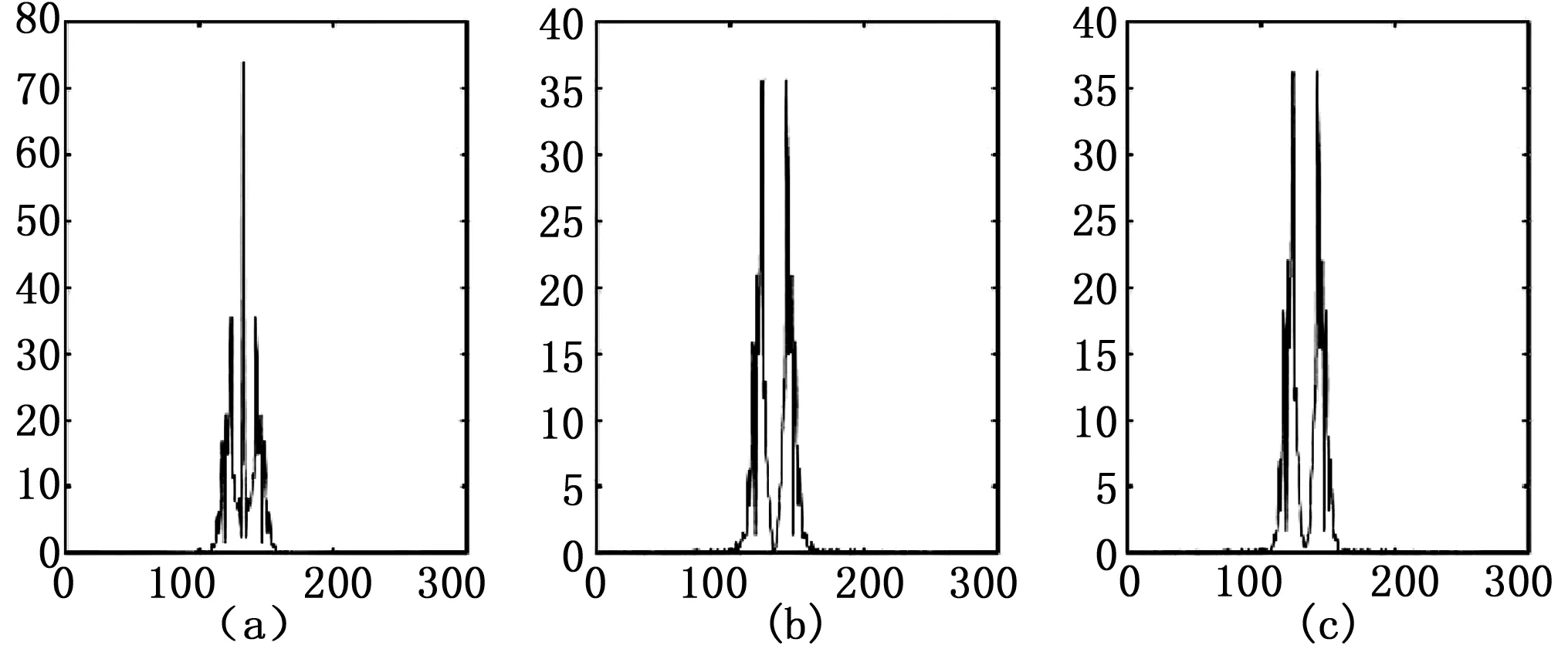
图9 目标条纹图红线标记强度分布的频谱图
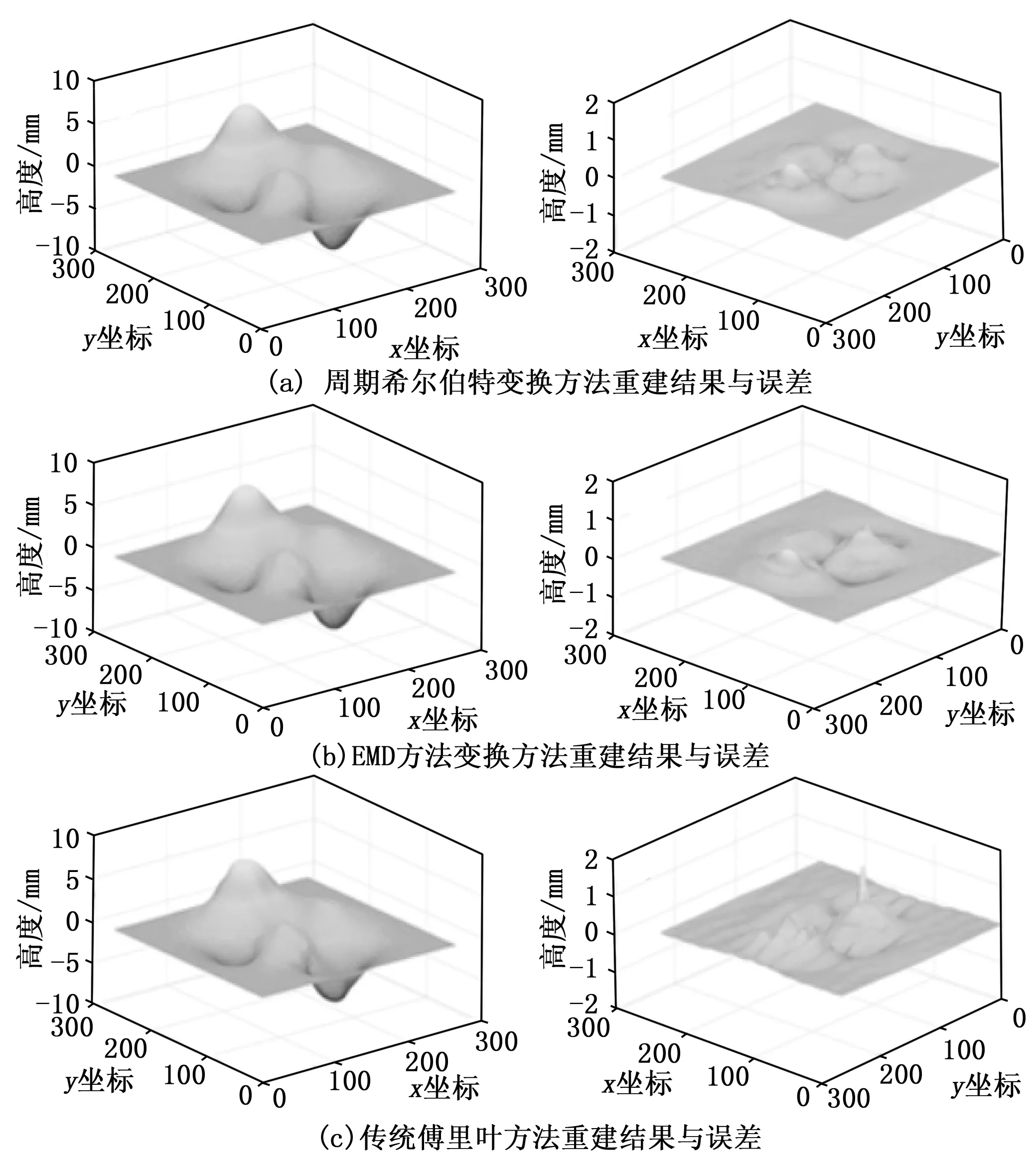
图10 传统傅里叶方法、EMD方法、周期希尔伯特变换方法重建结果对比
少了背景分量对重建精度的影响。对重建精度的比较如表1所示,消除背景分量能有效提高傅里叶轮廓术的重建精度,周期希尔伯特变换方法相较于经验模态分解方法能达到更好的重建精度。
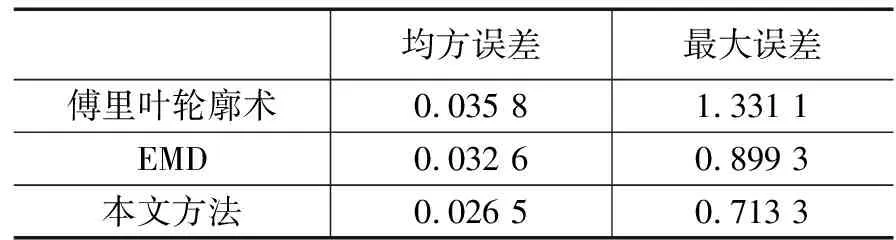
表1 误差对比
为了进一步讨论该方法受随机噪声的影响情况,在图6中分别加入了由rand函数产生的k次随机噪声,其中k从0变化到3.5,区间间隔是0.5。不同程度噪声下的均方误差分布如图13所示,从图11可以看出误差随着噪声的增加而增大,本文方法相较于EMD方法对噪声更具有鲁棒性。
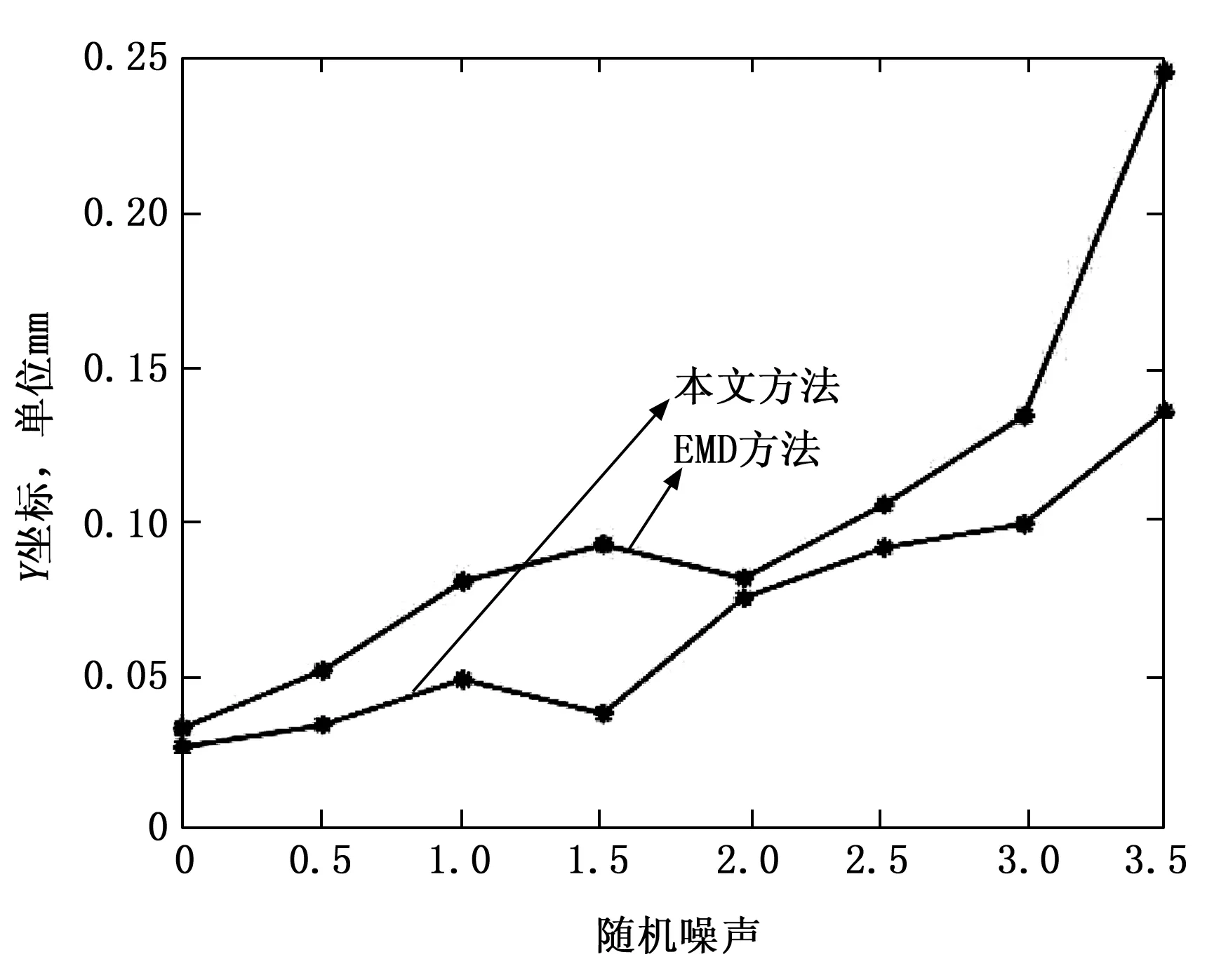
图11 不同噪声水平下的均方误差
4.2 实验结果与分析
实验首先对直径为20 mm的标准半球体进行测量。条纹产生设备是DLP投影仪。摄像机使用CCD靶面与定焦镜头,分辨率为1 920*1 280。投影条纹图如图13(a)所示。
图12(a)和图12(b)分别是条纹图使用EMD算法和本文方算法处理后的效果图。图12(c)和图12(d)分别是目标条纹图红线标识行强度分布经EMD算法与本文算法处理后的频谱图,相比较于图12(c),图12(d)在背景分量消除的更加彻底而且噪声更少。图13(b)、(c)、(d)分别是传统FTP方法、EMD方法和本文算法重建三维视图。

图12 效果对比
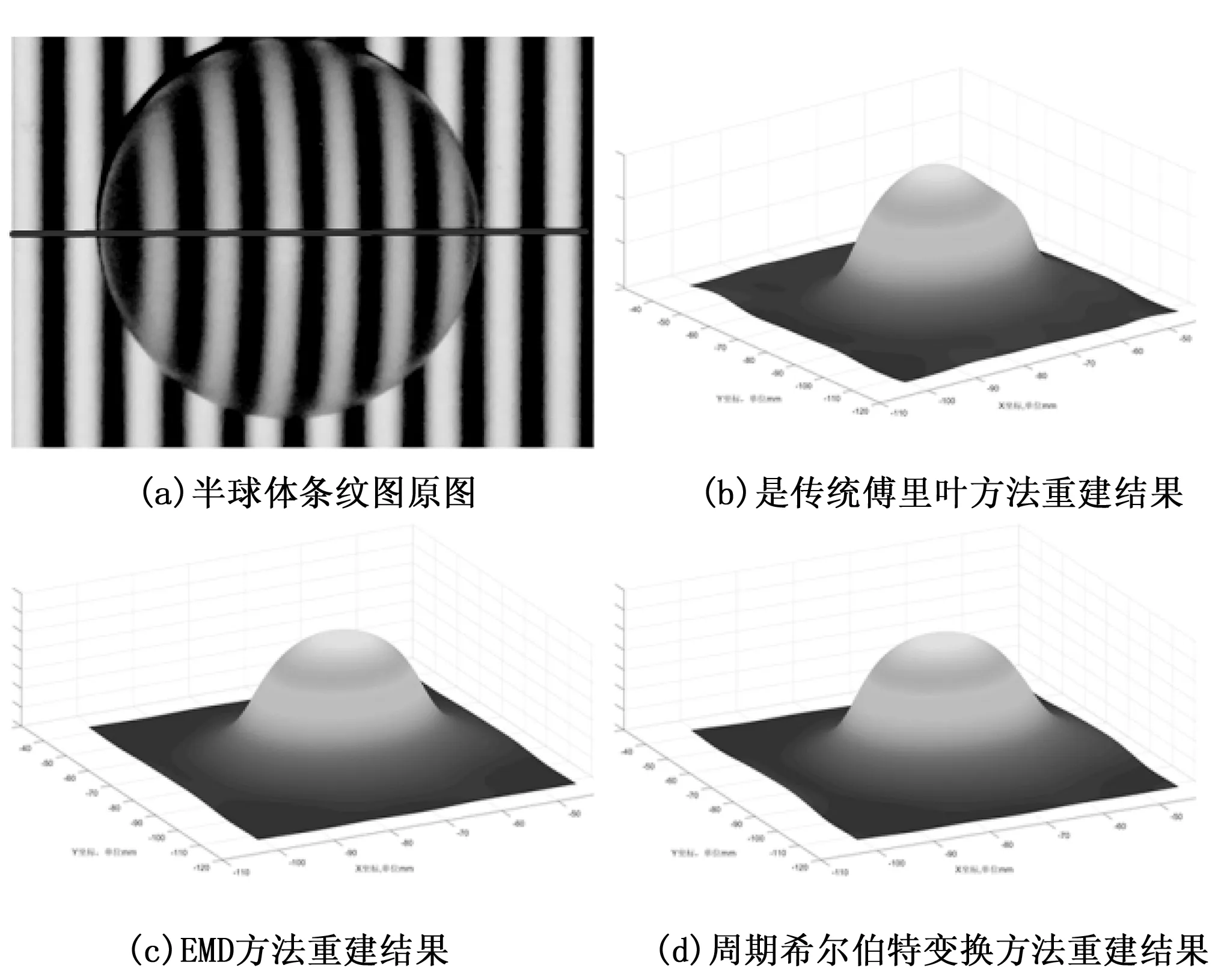
图13 三维视图
表2、表3为精度评估表,从表中可知相比于传统傅里叶轮廓术、EMD方法,本文方法在测量精度上分别提高了52.36%和19.82%。
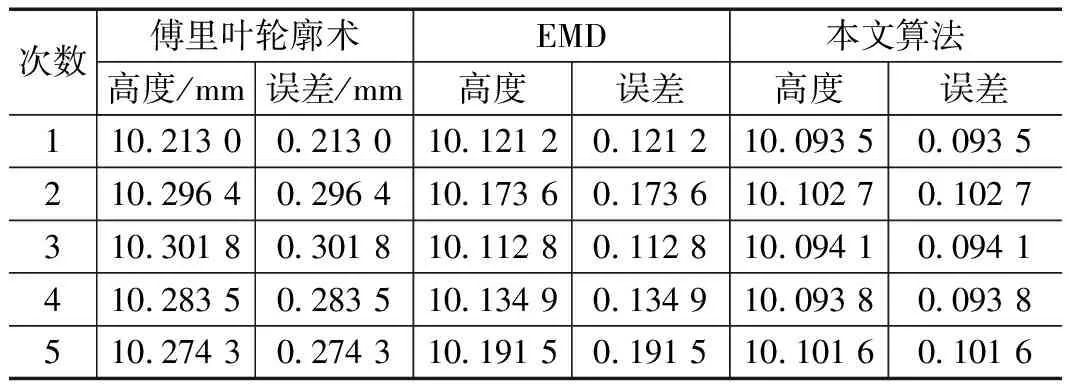
表2 测量结果与测量误差
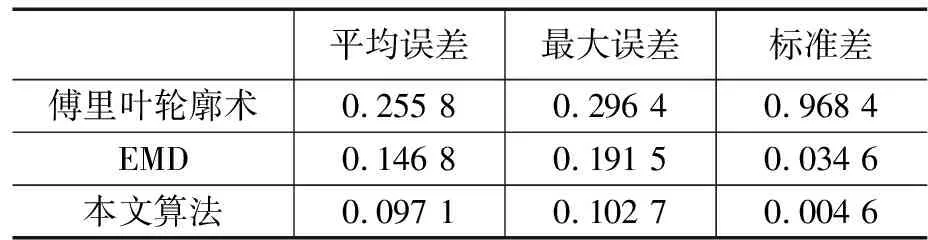
表3 测量误差分析
另一组实验对比了传统FTP方法、EMD方法和本文方法对手型的测量结果。实验如图14所示。为了更清晰的展示差别,用侧视图(如图15(a)、(c)、(e))来展示三维图像的细节部分。图15(b)、(d)、(f)分别是传统FTP方

图14 手型实验图

图15 三种方法局部图和全局图

图16 手型三维模型
法、EMD方法、本文方法恢复出来的三维图像的侧视图。由图可见本文方法恢复的手型三维模型相较于另外两种方法恢复的结果,没有波纹样的噪声,精度相较于传统的FTP方法有明显提升。与EMD方法相比也有一定的改进。这也为FTP方法应用于复杂面型的三维恢复提供了参考。
5 结束语
本文提出了一种逐周期条纹背景自适应去除算法,通过近似条纹图每个周期内的背景分量是一个常数,对条纹图每个周期分别进行两次希尔伯特变换,再把变换后的条纹周期组合成结果条纹图。只需要一张变形条纹图即可恢复出物体的三维形貌。计算机模拟与实验结果都表明本文所提方法在消除条纹背景方面具有良好的效果而且能提高FTP的测量精度。

