基于Hough变换和FFT多投影精测的织物纬斜快速检测方法研究

崔展豪,刘 剑

(上海应用技术大学 电气与电子工程学院，上海 201418)

0 引言

纬纱倾斜或弯曲严重影响布料成品质量，因此纬斜检测技术在纺织品生产中越来越受到重视。当前，纬斜检测正由第二代的光电检测法向第三代的基于图像处理的方法发展[1-2]。相比光电检测方法，基于图像处理的检测技术具有更高的准确率与适应性，正逐渐成为国内外纺织行业整纬设备的主流方向。

目前，基于图像处理技术的检测方法主要包括快速傅立叶变换(FFT,fast fourier transform)法、Hough变换法和Radon变换法等方法[3-6]。文献[7]运用傅里叶变换将图像转换为突出显示强度变化最大的区域的形式，检测出由于磨损处理或构造而产生的纹理细微差异。文献[8]等一批学者对织物图像进行了傅立叶变换，把这些织物的图像从在时间域分析转换为在频率域进行分析。利用FFT变换法分析出在织物图像中能量频谱线曲线中的峰值点，求得在织物图像中的经纱和纬纺布的密度，并与人工检测做了对比，结果表明其算法对三种类型的织物具有良好是适用性。文献[9]率先采用投影离散傅里叶变换(DFT，discrete fourier transform)及多角度投影分析方法对织物图像能量功率谱中两次循环多角度旋转投影根据其中心区域投影的最大值，检测出织物图像倾斜角度，测量误差在0.5度以内。文献[10]提出了基于霍夫变换和快速傅里叶变换，对进行的织物图像的频谱图进行霍夫变换而直接可得织物纬纱、经纱和斜纹方向信息。文献[5]于2007年采用Radon变换的算法，计算了经纬纱密度、自动化方式解析织物组织属性与检测织物纬斜方向，该文章使用小波变换对织物的图片结构进行了分解和重构，利用 Radon 变换算法对织物进行了倾斜程度的检测和纠正，计算出织物结构和属性的自动识别及经纱、纬纱密度的计算。文献[11]提出基于Radon变换将织物纬斜检测问题转化为峰值搜索问题，采用全1矩阵使方差-偏斜特征曲线输出为单峰曲线，检测误差在0.15°以内。

在实际应用中，DFT变换法可以利用其旋转不变性精确标出倾斜程度，但由于运算量较大，在部分程度会限制了其在数字信号处理上的使用；Hough变换法容易由于原始图像中存在较多的干扰信息，导致算法不能精确的提取表示纬斜方向的直线；Radon变换受到计算机进行从笛卡尔坐标系到极坐标转换过程中插值误差的影响检测直线的精确度，和计算直线积分时受到硬件随机读取性能的限制。

因此，在保证纬斜检测精度的前提下，尽可能缩短检测时间，满足工程实际应用需求，已经成为当前纬斜图像检测急需解决的关键问题。本文提出一种结合Hough变换和快速傅里叶变换(FFT)多投影精测方法，运用Sobel边缘方向和骨架检测等图像处理手段的织物纬纱倾斜快速检测算法。

1 纬斜快速检测算法原理及其框架

按标准生产的织物中经纱和纬纱交织成有一定规律和方向的纹理。而已经加工编织好的织物由于经过高温漂洗和人工染色等各种特殊原因，通常它们都会出现由于编织两端所拉伸而导致承受力不均匀等问题，而导致其经纬纱纹理的无规律弯曲的倾斜情况。

提出的新纬斜快速检测算法原理框架如图1所示。首先通过傅里叶变换对图像进行频域滤波，然后使用Sobel边缘方向检测的算子对图像进行卷积以得到边缘方向图，接着用形态学滤波得到骨干图，最后进行Hough变化和多投影分析得到织物图像的纬斜角度。具体步骤如下：

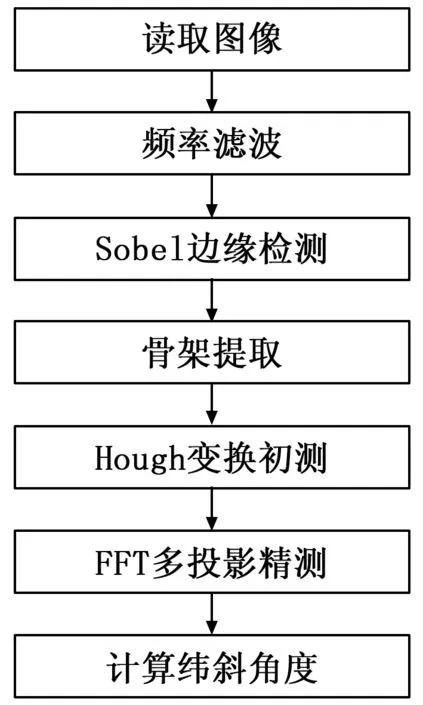
图1 纬斜检测快速算法流程图

1)读取图像转化为灰度图像显示，对灰度图像使用理想高通滤波器进行频域滤波，增强其纬斜特征；

2)使用Sobel算子进行卷积，通过对边缘特征检测来增强图像纹理；

3)进行形态学骨架化处理，消除干扰信息简化图像增强特征，提取纬斜纹路的中心线；

4)进行Hough变换直线检测，初步测出纬斜方向，得到初测角度；

5)在初测角度±1°范围内，以0.1°步长进行旋转投影，测出准确的纬斜角度。

2 织物图像频域滤波

织物图像可以视作一类具有特别排列纹理的图像，其最显著的特征是经、纬纱以特定方式的周期性排列。则图像信息可以视为由两个变量x，y构成的离散二元函数f(x，y)。

通过相机对织物纹理进行拍照，并将图像裁剪并转化为大小合适的灰度图像。对图像进行傅里叶变换，如公式(1)所示。

(1)

式中，u，x= 0，1，2，…；x，y为时域变量；u，v为频域变量。

通过分析傅里叶变换得到频谱能量图，发现其能量分布与织物图像的经纬纱纹路走向垂直[12]。其中大部分区域都是灰度变化缓慢的区域，即织物图像中背景和纬纱主干部分；只有一小部分是灰度变化剧烈的区域，即包含纹路的边缘，表示纹理的方向。

因此，在图像傅里叶变换频谱能量图中，设置理想高通滤波器可以滤除作为干扰信息的背景部分的低频信息部分，保留作为表达织物经纬纱纹路部分的高频信息部分。由图2可以看出，频谱图中高频信息部分(即图中灰度值较高，表现为较亮的区域)一般分布在图片的四周角落，而低频信息部分(即图中灰度值较低，表现为较暗的区域)一般分布在图片的中心区域。

图2 理想高通滤波前(左)后(右)的频域图

故为滤除中心区域的信息，设置理想高通滤波器的传递函数H(u,v)为：

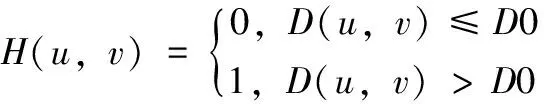
(2)

其中:D0表示截止频率，D(u，v)是到频谱中心的欧式距离，计算公式如下：

(3)

式中,M和N表示频谱图像的大小，(M/2，N/2)即为频谱中心。在频域滤波后，运用公式(4)对新的频谱能量图进行傅里叶逆变换得出处理后的图像。

(4)

从图2可见，频域滤波后纹路信息更加清晰明显，滤除掉含有干扰信息的灰度变化，使得之后的直线检测能够更加精确。

3 Sobel算子边缘方向检测

由于实际拍摄的图像中，不同层次的或拍摄不清的边缘之间相互混合在一起，同时还因为设备问题出现一些噪声。频域滤波一般情况下会将边缘和这些噪声作为高频信息而保留下来。因此，需要借助边缘检测方法来进一步处理图像。常用的边缘检测算子有Prewitt算子、Laplacian算子、Canny算子、Roberts算子和Sobel算子：其中Prewitt算子先计算像素平均值，再计算差分求得梯度值，能抑制噪声，但容易造成误判而定位不准确；Laplacian算子具有各向同性和旋转不变性，同时也会对噪声非常敏感，需要先进行高斯平滑预处理抑制噪声；Canny算子能滤波降低噪声和增强边缘，但程序较为复杂且运算速度不高；Roberts算子定位较准确但鲁棒性较差，在噪声较大的织物图像中边缘定位精度不高。对比各类边缘检测算子，这里选用精度较好抑制噪声好适用于灰度渐变低噪声的Sobel算子[13-14]。

Sobel算子是图像边缘检测中最常用的工具之一，由两个方向的卷积计算因子组成，其中，水平卷积因子Mx和垂直卷积因子My为：

(5)

(6)

对图像像素点使用卷积因子Mx和My进行卷积运算，计算出像素的梯度值及其绝对值，并根据设定的阈值来过滤。设A为被处理的原图像，则其水平梯度dx计算公式为：

dx=Mx*A

(7)

其垂直梯度dx计算公式为：

dy=My*A

(8)

由此分别可以得到水平方向及垂直方向的灰度差分近似值，能计算出每个像素点的梯度值，其梯度T计算公式为：

(9)

计算出的梯度值与阈值进行对比，当梯度值小于设定阈值时，将该像素点数值置0，否则置1。边缘判别式为：

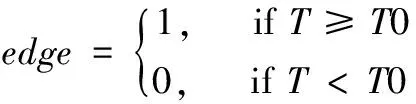
(10)

边缘提取后的图像如图3所示，可以看出图中仅保留了纬纱干路部分而滤除背景部分，并且转化为二值图像，极大简化了图像信息。

图3 与Sobel算子卷积后边缘方向图

4 骨架提取

通过分析边缘提取后的图像可以发现，纬纱纹理具有较多毛刺状凸起部分。这些毛刺会影响Hough变换的准确性，使得直线提取到错误方向上；并且还会增加进行变换像素点的数量，从而使计算时间延长。因此在进行Hough变换之前还需通过形态学骨架提取运算来突显纬斜纹理的走向[15]。

骨架提取的核心思想是从目标对象外围往对象中心，利用以待检测像素为中心3*3像素窗口的特征，对目标不断腐蚀细化，直至不能再腐蚀(达到单层像素宽度)，就得到了图像的骨架[16]。

关于骨架提取的算法，一般分为迭代和非迭代两大类。在迭代算法中，又分为并行迭代和顺序迭代两种。本文使用Zhang-Suen并行迭代算法[17]。该算法迭代满足的特殊条件如下。

假设图像中某一像素点及其周围的点阵为：

P9P2P3

P8P1P4

P7P6P5

(11)

定义，B(P1)为P1点的非零邻域的个数，A(P1)为P1点周围8个像素点灰度值按顺时针方向以0到1顺序排列的个数。当满足以下全部条件时，则该像素点被删除：

1)2≤B(P1)≤6；

2)A(P1)=1；

3)P2*P4*P6=0或P2*P4*P8=0；

4)P4*P6*P8=0或P2*P6*P8=0。

迭代计算骨架提取直至骨架为单像素宽度后得到图4中骨架化提取后的结果。可以看出，提取的纬纱骨架上仍有许多毛刺，这会影响之后检测直线的精度。毛刺的特征是从端点开始到分支点中间区域是小于设定的阈值长度的分支线段，根据该特征可以设计相应的算法消除毛刺。这里参考使用叶福玲的改进的图像骨架提取算法来去除多余的骨架毛刺[18]。具体算法如下表示为：

图4 形态学骨架化提取后图像

在式(11)中，假设P1为骨架上一个像素点，计算该点的B(P1)，当出现以下情况是：

1)当B(P1)≥3时，记P1为分支点。

2)将分支点置0，该点原分支方向成为断开的多个分支线。在设置范围PL内，分别计算断开后每个分支线段的长度Li，即记录该分支线段上像素点个数。

3)设置阈值PT(PT≤PL)，当PT≥Li时，删去该分支线段，否则保留该分支线段。

4)将之前置0分支点重新置1，连通未删除的分支线段。

在选取适当的阈值后，进过迭代计算得到图5中改进后的消除骨架毛刺运算的结果，可以改进后的骨架提取算法能够有效消去骨架上的毛刺，并能保持骨架线的连贯性，得到的纬纱干路部分进过后变得更加精细，进一步简化了图像信息。

图5 改进的消除骨架毛刺后图像

5 Hough变换纬斜角度初测

在可参数化几何图形检测中，Hough变换是一种广泛使用的方法。Hough变换于1962年由PaulHough首次提出，是一种参数估值计算方式，使用自动投票统计算法，利用图像空间中一点与霍夫参数空间正弦曲线的对偶性，把在图像空间中的检测对象转换到参数空间的对应目标。通过求取在变换到参数空间后对局部范围计算累加求和的最大值，最后求得一个满足该特定条件的集合，以此计算出图像中最符合直线特征的点集合的方向。

其计算原理是将原图像空间中坐标为(x,y)的一点，其按照式(12)转变为以(r,θ)为参数的Hough空间中一条曲线。

r=xcosθ+ysinθ

(12)

Hough变换检测直线的实质是将对于平面中每个确定的点，按照上述公式在霍夫参数空间中转化为正弦曲线，其中部分曲线会相交于一点，该点表示这些曲线所对应的点在原空间中共线所在的直线。找出统计所有的被记录次数最多的(r,θ)及其所对应的直线，则表示该直线在平面内被最多点共线次数最多[19-20]。

即可以得出Hough变换直线检测步骤：

1)对骨架提取后的图像进行霍夫空间变换，变换的精度设定为Δθ=0.2°；

2)在规定区域内找到霍夫空间变换的峰值；

3)对这些峰值按照由大到小顺序进行排序；

4)选取最大值。

图6为Hough变换的结果，图中标出的其中三个峰值表示原图中三个最具直线特征的方向。通过对比分析计算，可以得到纬纱方向的角度。

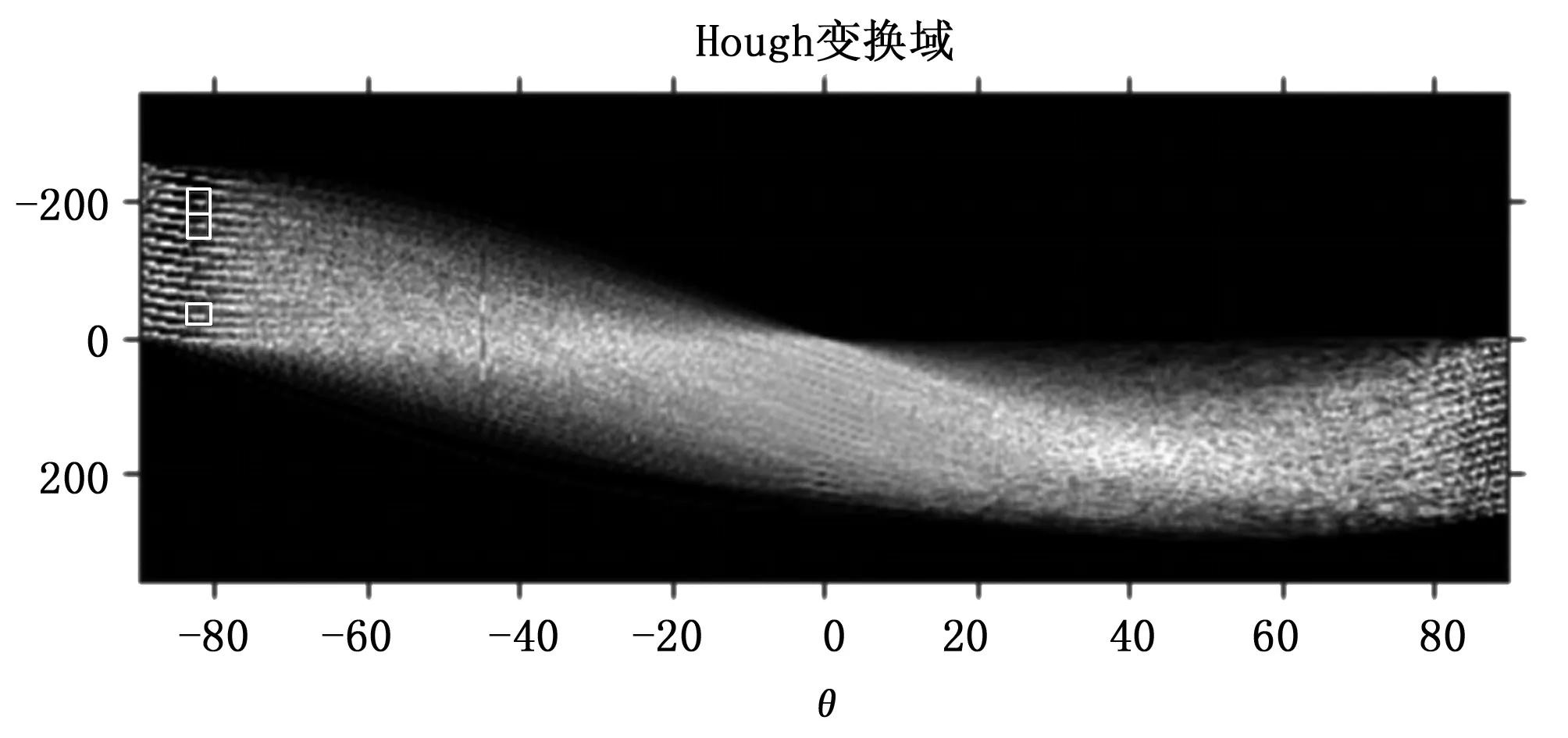
图6 Hough变换参数空间中的峰值

6 FFT多投影精测

通过Hough变换，可以快速地检测出纬纱倾斜角度，但该方法的精度有待进一步提高。因此，需要使用FFT多投影方法在初测角度附近进行精确检测。

FFT多投影精测的原理是利用快速傅里叶变的频谱图的旋转不变性。即二维信号(图像)在空间域上向某一方向旋转一定角度，则其二维傅里叶变换在频域上的频谱图也会在相同的方向上旋转相同的角度[21-22]。

图7给出了织物灰度图像的傅里叶变换频谱图(左边图像)和旋转一定角度的频谱图(右边图像)。从图中可以看出两个方向的高频信息，分别表示原灰度图像中水平方向和垂直方向上信息的变化情况。反应在原织物图像，就是经纱和纬纱的方向倾斜情况。

图7 织物频谱图(左)及其旋转后的频谱图(右)

当原图中纬纱方向相对于水平方向存在一定角度的倾斜时，在频谱图的垂直方向也倾斜相应角度，此时将频谱图向x轴进行投影，统计中心区域像素点集合，得到的值不是最大值；而当图像旋转该倾斜的角度后，频谱图中垂直方向的信息投影后中心区域的投影点集合数值是最大值。

以Hough变换检测直线得到的初测角度为中心位置，在±1°范围内以0.2°间隔进行旋转和投影。只有当图像中纬纱纹理方向与水平方向最大限度平行时，其投影中心区域的点集合会出现峰值。为了减小误差，以中心点左右3列像素的总和进行比较。通过计算峰值所对应旋转的角度是相对于由Hough变换检测的初测角度的偏离角度。

图8给出了旋转前(左图)和旋转后(右图)的中心点附近频谱信息投影图。从图中可以看出，在未旋转一定角度前，峰值信息含有两个峰值，表示此时峰值频谱信息较为分散，并不是最大值；在经过旋转一定角度后，峰值频谱信息更加集中突出，表示该角度出现只有一个最高的峰值是中心区域像素点个数的最大值，旋转的角度加上Hough变换初测的角度就是织物的倾斜角度。

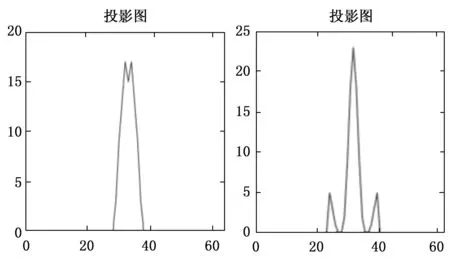
图8 频谱信息投影图

7 实验结果与分析

本次实验的硬件平台采用Windows10专业版系统，intel®CoreTMi7-7700HQ处理器，ST2000LM015-2E8174硬盘，Crucial-DDR4-2400MHz-8G*2内存，Intel(R)-HD Graphics-630显示适配器，Canon-EOS-1D-X-Mark-II/ Canon-EF-24-70mm-f/2.8L- II -USM相机，软件平台使用MATLABR2018b。为进一步验证本文所提出方法的有效性，选取四种不同类型的织物进行图像拍摄，并将每幅图像大小裁剪为512×512像素，每次检测重复10次并取平均值以消除误差。对四类织物图像，采用单独基于Hough变换方法、单独基于FFT多投影方法，以及本文提出的结合Hough变换和FFT多投影精测方法分别进行纬斜角度检测，并进行对比。

表1给出了基于Hough变换方法的检测结果。从表中可以看出，使用该方法检测误差最大达到1.8°。这是由于采样图像中存在较多的冗余信息，包括颜色图案、明暗差异、编织工艺差别等干扰因素，导致进行Hough变换提取直线不能精准表达纬斜方向，终检测结果误差较大。该方法由于同样经历频域滤波，按比例二值化的预处理，剩余需要变换的像素点可以控制在较少的范围内，因此耗时都不大于0.3 s，速度较快。因此适用于快速初测。

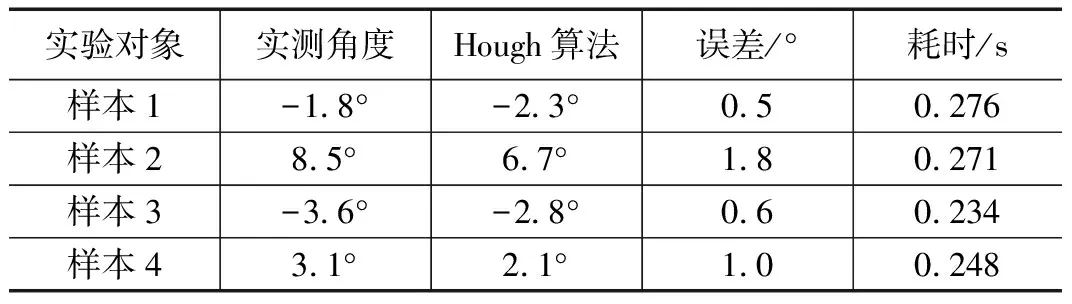
表1 基于Hough变换方法的检测结果

表2给出了基于FFT多投影方法的检测结果。从表中可以看出，基于DFT的多角度投影算法，根据较小旋转的步长能够完成较为精确的检测纬纱倾斜角度较小的织物，并且面对疏密程度略大的织物时，该方法能表现出良好的适应能力。但因为检测范围较大、检测精度较高而进行较多次投影导致迭代计算量较大而实时性较差。

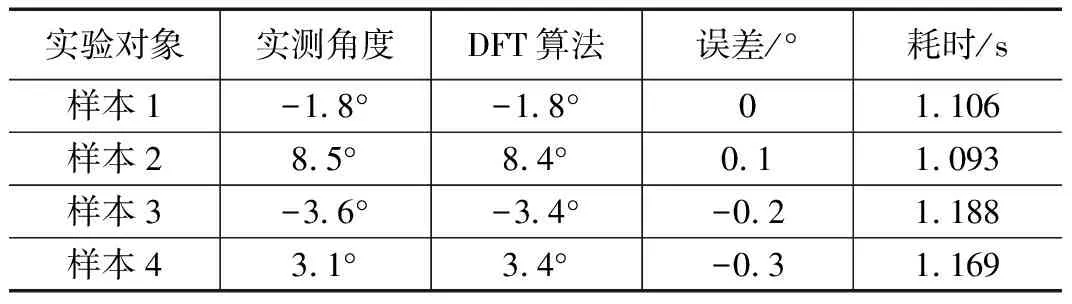
表2 基于FFT多投影方法的检测结果

表3给出了基于Hough变换和FFT多投影精测方法的检测结果。从表中可以看出，最大误差为0.2°，平均耗时0.533 s。与FFT多投影方法相比，该方法测量精度相当，耗时提高了约53%。因此，该方法能够较好兼顾检测精度和计算速度，适用于工程实际使用需求。

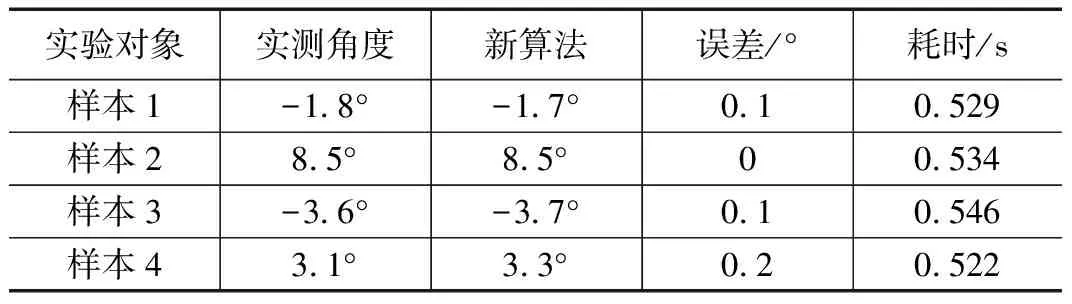
表3 结合Hough变换和FFT多投影精测方法的检测结果

8 结束语

本文为实现对不同类型织物能够快速准确地检测出其纬斜角度，提出了一种结合Hough变换和FFT多角度投影的织物纬斜检测算法。对织物图像进行频域滤波来增强织物图像的纹理特征，利用Sobel算子对纬纱进行边缘方向检测，进行形态学骨架化提取以简化图像信息；使用Hough变换快速检测出纬斜的初测角度，最后在初角±1°范围进行FFT多角度旋转投影确定精确的纬斜角度。

实验证明，该算法有效解决了单独使用Hough变换精确度不高，以及单独使用DFT多角度投影有足够精确度但耗时过长的问题，兼顾检测精度和计算速度，满足机器视觉整纬器的精确性、实时性和通用性要求。