SPH 粒子法在高速冲击连接问题中的应用
孙 标,廖秋慧,何建萍
(上海工程技术大学 材料工程学院,上海 201620)
0 引言
高速冲击类问题由于速度高,物理过程难以观测,还具有一定的破坏性。然而高速冲击却具有潜在的应用,如在焊接方面,高速冲击可以实现固态连接。基于材料的状态,可对焊接技术分类,可分为固态焊接和熔化焊接[1]。熔化焊接是利用金属熔化原子扩散,经一定时间冷却后实现冶金结合;固态焊接是低于材料熔点条件下将材料结合在一起。因为熔化焊接会在焊缝处出现金属间化合物,金属间化合物属于硬脆相,其将严重影响材料连接后的性能。因此,高速冲击连接异种材料的固态连接方法具有很好的应用前景。实现高速冲击连接,关键点是要呈现出连接界面处的有规律的界面波[1],如图1 所示。

图1 界面波Fig.1 Wavy morphology observed
数值模拟成为现实中工程问题以及科研问题的重要研究手段,该技术为物理世界的现象理论提供了试验和检测,并辅助理解工程中复杂问题,同时可指导工程应用。数值模拟的关键点是需要将连续体离散化进行计算。有限元法(FEM)和有限差分法(FDM)是基于网格划分进而离散,然而传统Lagrangian 算法对于大变形以及冲击类问题,由于冲击使得网格变形,该算法很难处理与原始网格不一致的网格,并造成不连续界面;同时,为保证不连续界面的一致性,通过不同时刻网格重构计算,会增加计算成本,同时网格畸变过大导致计算终止[2]。绝对拉格朗日-欧拉算法(Arbitrary Lagrangian-Eulerian)可模拟冲击大变形问题,例如:利用ALE算法研究弹塑性入水冲击问题,水下爆炸冲击。
无网格方法的关键思想是使用一组任意分布的节点或粒子为具有各种可能边界条件的积分方程或偏微分方程提供准确和稳定的数值解[3],光滑粒子流体动力学(Smoothed Particle Hydrodynamics,简称SPH)方法是无网格法中的一种,该方法最早解决三维天体物理学中行星运动和碰撞问题,后被广泛应用于流体动力学,冲击模拟,爆炸焊接,水下爆炸冲击等问题。本文将以旋转的子弹作为研究对象,该问题关键在于当子弹具有一定的转速后,简化为二维问题,难以观察其旋转的影响,必须利用三维SPH 粒子法,这也会导致SPH 粒子数增多,进而会增加模拟计算的时间。
综上,本文将对比网格法FEM 与SPH 粒子法的数值模拟结果,确定合适的模拟方法;为子弹冲击连接进一步研究做探索,并对比子弹在有无转速条件下的界面波形貌;最后,将FEM 网格法与SPH 粒子法进行耦合模拟,确定冲击连接合适的算法模型。
1 理论算法概述
1.1 ALE 算法
ALE 算法是将网格建立在物体上,但是网格既可随着材料的变形而变形,也可以保持在空间中不动,甚至可以在空间的一个方向保持固定,在另一方向随物体的运动而运动[4]。在每一个时间间隔的计算中有两个阶段,第一阶段计算时,根据质量、动量、能量守恒方程运用拉格朗日算法获得平衡方程(1)和(2)[5]:
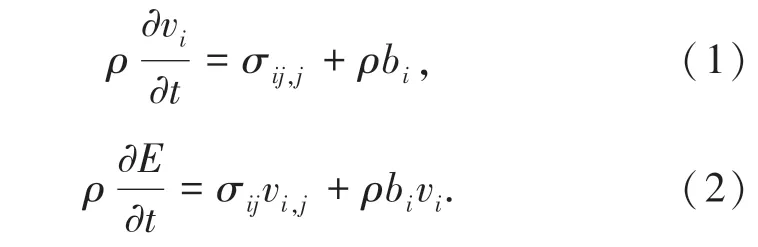
在第二阶段中,需要将发生移动的网格重新映射到最初的位置,并计算穿越网格边界的动量、质量,网格节点根据公式(3)和公式(4)更新速度与位移。

其中,u为网格速度;Fext为外力矢量;Fint为内力矢量;M为质量对角矩阵。
1.2 SPH 光滑粒子法
SPH 的核心是核函数,其可以被理解为一种在一定范围内其它临近粒子对研究粒子影响程度的权函数,核函数的近似积分表示任意一点的场函数及其导数,最后在偏微分方程组中运用粒子近似法,得到只与时间相关的常微分方程[6-7]。SPH 算法一般需要两个步骤,第一步是场函数核近似(kernel approximation),第二步是粒子近似(particle approximation)。
对于任意连续宏观变量(密度、温度、压力等),函数f(x)可用表达式(5)描述[8]:

对场函数导数,其可近似为式(6):
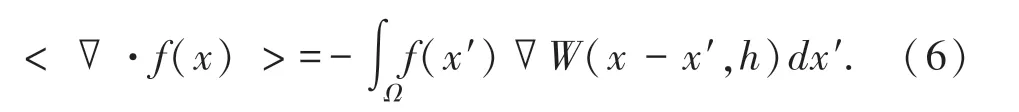
其中,Ω为求解域;x为待求粒子在空间中的坐标;x′为待求粒子在求解域内的相邻粒子在空间中的坐标,经过函数核近似计算,上述场函数及其导数均可转化为场函数的值及核函数的积分表达式;W(x-x′,h)为核函数,满足归一化条件和紧支性条件[9-10]。
核函数W的选取决定粒子紧支域大小以及核近似和粒子近似的精度[3]。常用核函数包括钟形、高斯型、分段三次样条核函数。
在SPH 算法中,粒子近似法作为SPH 的第二个关键步骤,在核近似过程中将场函数转化为近似连续性积分方程后,通过粒子近似法,得到相邻粒子的叠加求和的离散形式。粒子近似法如图2 所示。
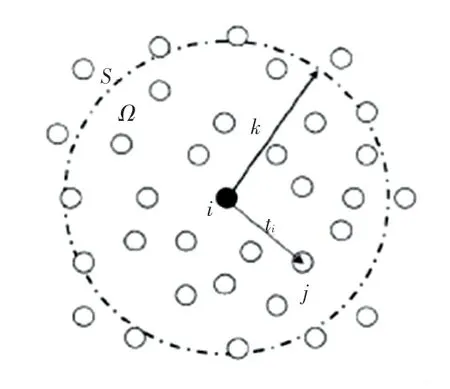
图2 粒子近似法Fig.2 Method of particle approximation
若将积分近似式中表示粒子j处的无穷小体积dx′用离子体积ΔVj代替,则粒子质量mj表达式(7):

其中,ρj为粒子j的密度。
第i个粒子的核近似函数f(xj)最终转化为粒子近似[3],式(8):
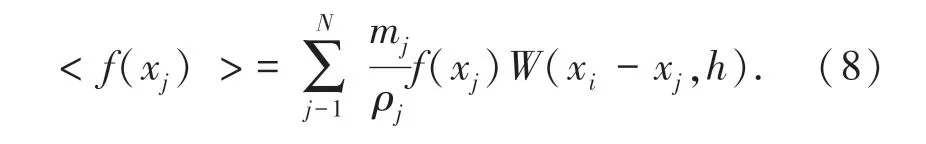
2 数值模型建立
2.1 几何模型及材料参数
采用圆柱型子弹冲击平面的基板建立数值模拟模型。子弹材料为铜,基板材料为低碳钢材料,性能参数见表1。模型的尺寸分别是φ9×6 mm,10×10×5 mm,网格单元尺寸为0.02 mm,如图3 所示。相比网格法,SPH 粒子法,没有单元信息,取而代之的是节点信息。SPH 粒子建模过程是将建立好的有限元网格模型,在软件LS-dyna 前处理软件中SPH generation 功能将单元信息生成节点信息即可。

表1 模拟材料铜与低碳钢的性能[11]Tab.1 Property of material copper and low carbon steel[11]

图3 数值模型Fig.3 Numerical model
2.2 数值分析模型
由于子弹冲击基板属于大变形和高应变率问题,Johnson-Cook 方程的材料行为适用于强冲击载荷,式(9)。因此,选择了Johnson-Cook 模型作为模拟中子弹和基板的材料模型。

其中,εp是材料等效塑性应变;ε′p为材料实际应变率;为参考应变率;为无量纲的等效应变速 率;为无量纲的等效应变速率;T∗m =;T是无量纲温度;Tm是材料熔点;Tr是室温,A、B、C、n、m为材料参数。
材料模型参数见表2。

表2 铜与低碳钢J-C 本构模型参数Tab.2 J-C Constitutive model parameters of Copper and lowcarbon steel
当利用JC 材料模型时,必须有状态方程才能进行模拟计算。材料的状态方程与密度、压力及一些热力学参数有关,能够反应材料的体积特性。Grüneisen 方程适用于固体中的波的传播,能够与波阵面中的冲击跳跃存在直接联系,且方程中参数也可以通过实验确定。因此,子弹和基板材料模型的状态方程为Grüneisen 方程,其表达式(10)为:
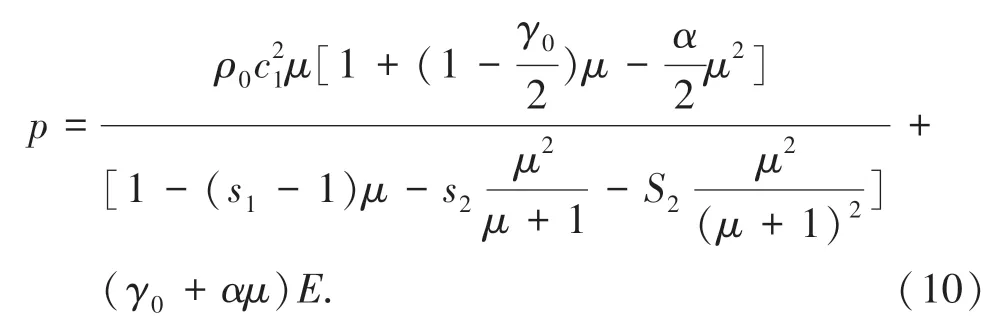
式中,ρ0为参考密度;C1为uS- uP曲线的截距;γ0、μ、α为Grüneisen方程系数;S1、S2、S3为uS-uP曲线斜率的系数;,V为相对体积;α为对γ0的一阶体积修正;E为材料内能。
子弹和基板的状态方程参数见表3。

表3 铜与低碳钢的状态方程参数Tab.3 Parameters of the equation f state for copper and low carbon steel
冲击连接可成功的速度范围一般在150~1 500 m/s[6]。因此,选取模拟的初始条件为:冲击速度为150 m/s,角速度1 177 rad/s;为更好对比有无旋转影响的影响,将冲击角度设置为0°,目的是有利于子弹施加旋转速度。
3 结果与讨论
3.1 ALE 网格法与SPH 粒子法界面处波形
分别对SPH 数值模型以及ALE 数值模型计算,获得如图4 所示的界面波。
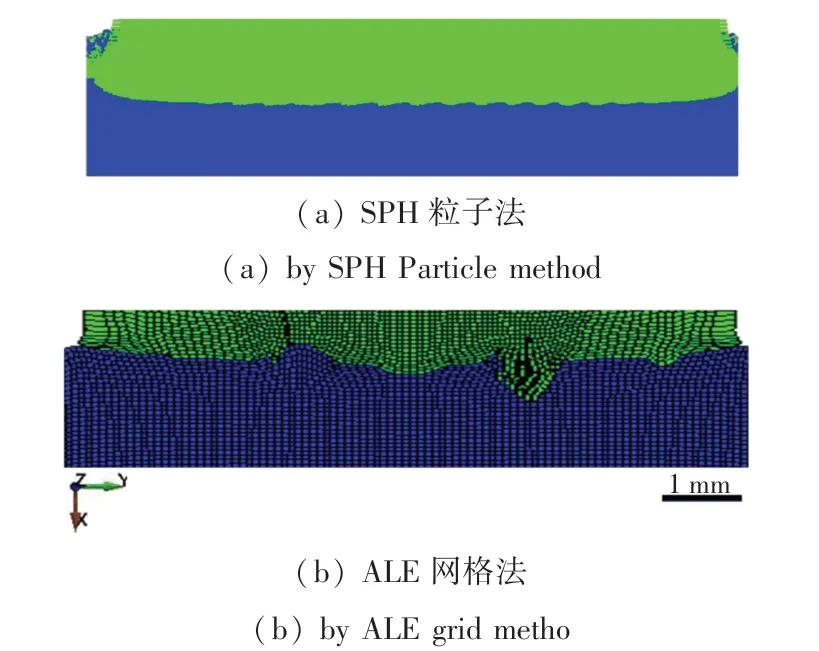
图4 SPH 与ALE 界面波形图Fig.4 SPH and ALE interface waveform
并对比高速冲击实验的界面波图1 与图4 模拟结果可知,采用SPH 粒子法可模拟冲击界面处波浪状的界面波形如图4(a);而采取ALE 网格法其冲击界面处出现较大的扭曲和网格畸变如图4(b)。因此,对于冲击类问题,SPH 粒子法呈现冲击过程的细节比ALE 方法合适。
在数值计算过程中不同算法会出现能量损失,算法是否合适,能量守恒可作为判断标准:工程上一般在10%以内的能量波动是可接受的。图5(a)和(b)分别为SPH 粒子法与ALE 网格法在Ls-dyna求解器中求得碰撞过程中的总能量变化;根据图5(a)可计算得SPH 粒子法总能量损失为9.8%,该值在可接受的范围内;图5(b)ALE 网格法能量损失1.3%,相比之下ALE 网格法能量损失较少。这是SPH 粒子法本身特点决定的,因为每个粒子是单独个体,碰撞后期部分粒子被冲击散落而失效。综合SPH 粒子法具有2 个特点:可呈现出界面处的界面波形以及能量损失在可接受范围内;因此,采用SPH 粒子法模拟冲击类问题更合适。

图5 碰撞过程的能量变化Fig.5 Energy change curve during collision
3.2 有、无转速条件下的界面波
SPH 算法明显的呈现出高速冲击连接的界面波形,为探索转速对界面处形成波形的影响,数值模拟了在冲击条件一致时模拟有、无转速条件下界面波差异如图6 所示。
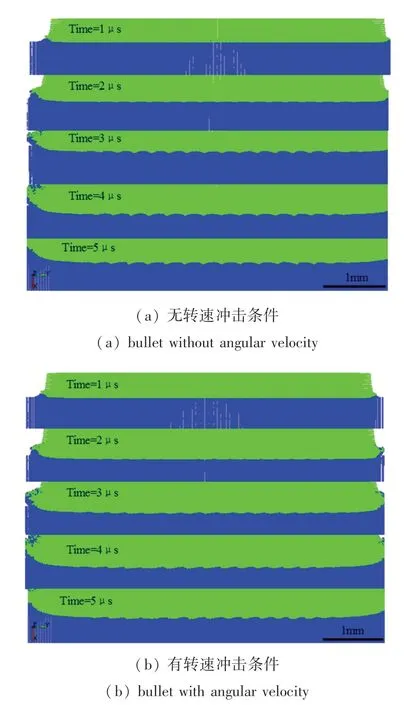
图6 高速冲击条件下界面波形成过程Fig.6 Formation process of interface wave under high speed impact
图6 中可观测到在有转速冲击条件下,界面处波幅较小,其原因是冲击过程中的赋予子弹旋转产生的切应力所致,具体地,主要受到τxy(X面上沿Y方向的切应力即图7 中xy-应力)的影响,图7(a)为在无转速的条件下产生的τxy切应力值为6 MPa,图7(b)为有转速的条件下界面处的τxy切应力值达到25 MPa。所以,利用SPH 数值模拟方法,研究旋转因素对界面波形貌影响具有可行性。
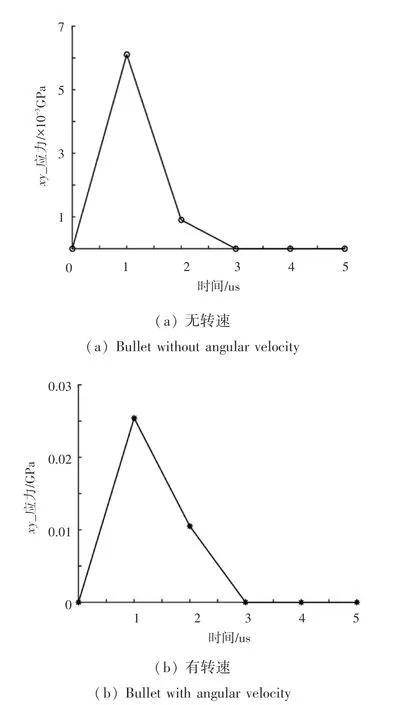
图7 xy_应力对比图Fig.7 Xy_stress contrast chart
3.3 ALE 与SPH 耦合
实际上,当三维问题的结构复杂后,SPH 算法建模所需的粒子数会增加,从而增加了计算的时间成本;为减少计算成本,通常是进行并行计算处理,简化模型,减少粒子数。并行计算可以减少需要计算设备的支持,不是所有模型都可以被简化,例如本案例,当有转速时候,很难获得转速对界面的影响。如果减少粒子数,无法呈现出界面波形,减少粒子数会增加计算误差,粒子数与计算精度关系如图8 所示。
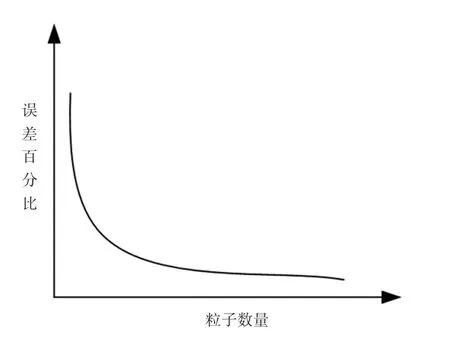
图8 粒子数与计算精度的关系Fig.8 The relationship between the number of particles and calculation accuracy
因此,本案例利用Ls-dyna 软件中的耦合关键字∗CONTAC _TIED_NODES_TO_SURFACE,将SPH 粒子单元与ALE 网格单元耦合;建模时对碰撞的非观察区域进行网格划分,观察区域进行粒子法近似处理,如图9 所示。最终模拟计算出ALE 与SPH 耦合的结果如图10 所示。
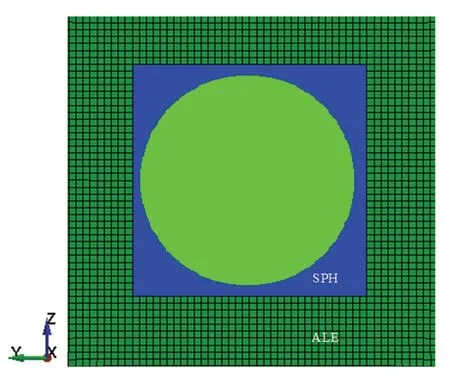
图9 ALE 与SPH 耦合模型Fig.9 Model of ALE and SPH coupling

图10 ALE 与SPH 耦合结果Fig.10 Result of ALE and SPH coupling
图10(a)中可以发现,耦合后界面处的波形没有任何影响,图10(b)为x面上y方向上的剪应力处于同一色块,应力传递具有一致性,意味着耦合的成功。即对于模型复杂或难以简化的模型,可采用ALE 与SPH 方法耦合的方法建模计算模型。
通过对比3 种不同算法模型单位时间计算的粒子数见表4,可确定当粒子数增加后,ALE 与SPH耦合的方式可减少直接利用SPH 粒子法的时间成本。这对尺寸较大,结构复杂的三维模型作冲击连接数值计算具有一定的借鉴作用。
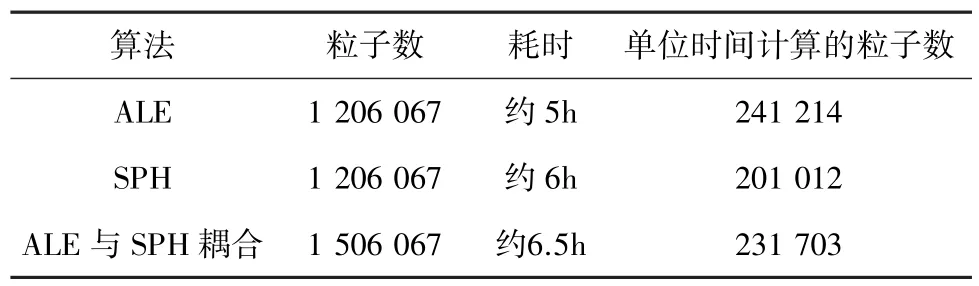
表4 3 种不同算法模型单位时间计算的粒子数Tab.4 Number of particles calculated per unit time by three different algorithm models
4 结束语
本文对比了ALE 法和SPH 粒子法旋转子弹冲击基板的案例,分析了SPH 粒子法更适合应用于冲击类问题,并针对SPH 粒子法存在的粒子数过多导致的计算成本增加,进行ALE 与SPH 粒子法耦合优化。综上,可获得如下结论:
(1)高速冲击连接问题,相比于ALE 算法,SPH粒子法能够很好的呈现连接界面的波形;同时,SPH粒子法也可呈现有转速与无转速时界面波波形差异,可研究子弹转速对冲击界面波形貌的影响;
(2)随着模型尺寸变大导致使用SPH 粒子法粒子数增加,耗时过长;ALE 算法与SPH 算法耦合的方式建模,可减少直接利用SPH 粒子法的计算时间。

