基于状态转移网络的汽车螺栓拧紧过程异常检测
李泽朋,顾长贵,宋雨轩
(上海理工大学 管理学院,上海 200093)
0 引言
一般来说,异常检测是指对环境中的异常行为,或者不符合预期行为的检测[1]。目前检测领域的复杂环境也给异常检测带来了巨大的挑战[2]。汽车制造领域的螺栓拧紧是通过对拧紧件(螺纹零件)施加拧紧力矩,使其拉伸形变产生轴力,实现被拧紧件之间相互夹紧的一种拧紧方式[3]。为了保证汽车出厂前车身各部位螺栓拧紧达到合适的拧紧力,以避免在汽车出厂后承担沉重的汽车召回代价,各汽车公司均会进行汽车出厂异常检测[4]。
基于规则、聚类、支持向量机和森林等参数统计模型和非参数统计模型常被用于做时间序列数据的异常检测[5]。但由于硬件要求高、操作困难、检测率不稳定等原因,大多数企业的实际检测过程中,通常由熟练的工程师利用现有的扭矩数据直接判断是否合格[6]。这一过程包含太多主观不可控因素,所以迁移性大大降低[7]。
随着数据量的增加,传统的方法在大规模异常检测中会遇到困难[8]。近年来,基于复杂网络的时间序列分析在各个领域引起了广泛的关注。通过将时间序列映射到网络,可以直观地得到从微观到宏观的不同时间尺度上的结构模式[9]。Lacasa 等人提出了一种广泛应用的可见图算法来连接相互可见的数据元素[10]。这种方法被迅速采用并广泛应用于不同领域提取嵌入时间序列中的信息[11]。
然而在上述方法中,时间序列均被投射到静态网络中,很难找到系统的动态进化行为[12]。复杂系统的动态过程可以由时间序列中具有预定义长度的序列段反映[13]。如果数据点彼此可见,将该段映射到可见图中,就是通过连接这些可见的数据点来实现[14]。对连续的可见图进行有向连接就会生成状态转移网络。在状态转移网络中,将节点定义为时间序列段内的状态,如果对原始数据由可见图方法产生的两个状态(可见图)之间连续,则两个状态之间存在有向连接。本文中状态转移网络中节点出现的频率称为度。如果原始时间序列构造的网络中节点的出现频率明显大于重组时间序列构造的网络中节点的出现频率,则将该节点称为模体,其可以作为时间序列的全局代表[15]。为了判断模体的出现是否具有长期记忆性,应用去趋势波动分析(DFA)理论计算了模体的Hurst 指数,并对其网络特征进行判别[16]。
本文试图通过对汽车拧紧过程时间序列构造状态转移网络,并分析不同序列之间网络的特性,进而来扩展和验证可见图方法,并验证汽车拧紧过程的数据中是否存在着非孤立的相互依赖的模体状态。在本研究中提出应用状态转移网络的方法建立异常检测数据网络,找出状态转移网络中合格与不合格数据的差异,从而实现异常检测的功能。
1 异常检测方法
1.1 数据描述
本文中用到的数据由上汽集团汽车出厂检测部门提供,包括5 组合格汽车螺栓拧紧过程时序数据(后文简称合格汽车拧紧过程序列,即TSQP)与5组不合格汽车螺栓拧紧过程时序数据(后文简称不合格汽车拧紧过程序列,即U-TSQP)。图1(a1~a5)为5 组合格汽车拧紧过程时序图,(b1~b5)为5组不合格汽车拧紧过程时序图。
如图1 所示,(a1)-(a5)为5 组合格汽车拧紧过程时序(简称,TSQP)图,(b1)-(b5)为5 组不合格汽车拧紧过程时序(简称,U-TSQP)图,其中x轴代表拧紧时间(ms),y轴代表扭矩值(N/m)。
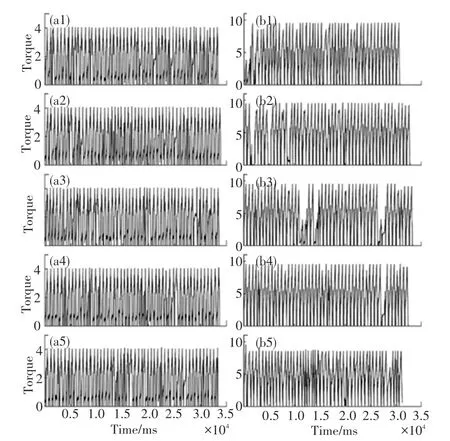
图1 汽车拧紧过程时序图Fig.1 Time series diagram of automobile bolt connection process
状态
时间序列可表示为X ={x1,x2,x3,…,xN},其中N为序列长度。首先,由滑动窗口长度s沿时间序列从前向后滑动,可得到一系列相互重叠的滑动窗口长度的时间序列片段Xm ={xm,xm+1,xm+2,…,xm+s-1},其中m =1,2,3,…,N- s +1。
构造状态转移网络的可见图方法对应的滑动窗口长度选择为s =5。通过可见图方法,每个时间序列片段可被转化为一个可见小图。在可见小图中,节点被定义为该时间序列片段中的数据,同一个可见小图中各节点之间是否可以连边由各节点是否可见决定,其数学形式表述为:如果处于xa和xb之间的每个点xc都满足公式(1):
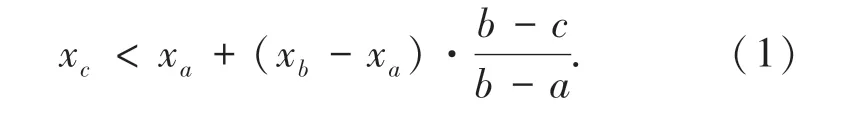
为此,在取滑动窗口长度为s =5 时,对所有数据利用可见图方法构造可见小图之后,可以得到其所有的可见小图,即状态转移网络中所有的状态,如图2 所示。
如图2 所示,汽车螺栓拧紧过程时间序列中观察到的状态。在图片的左上角为每个状态分配了一个标识号。共有10 组不同的序列,每组都产生了如图2 所示的25 种状态。
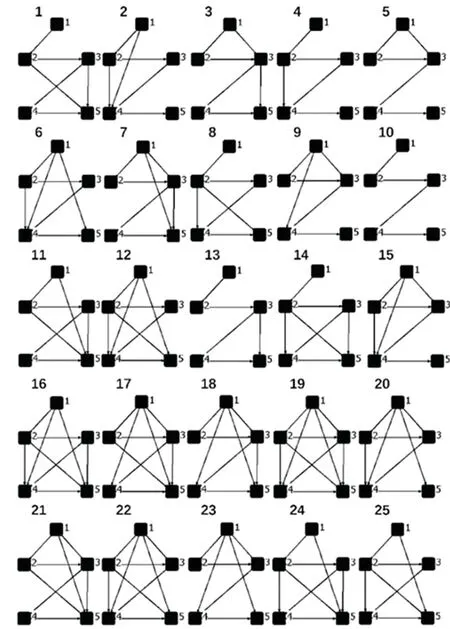
图2 汽车拧紧过程时序状态图Fig.2 Time series state diagram of automobile bolt connection process
在此用gk表示邻接矩阵,并用之代表某个滑动窗口长度s内的数据点构成的可见图结构。如果该滑动窗口长度s内的数据点xa和xb相连,则邻接矩阵元素gk(a-k +1,b +k +1)的值为1;否则,值为0。由此方式可将原式的整个时间序列{x1,x2,x3,…,xN} 映射为邻接矩阵序列G ={g1,g2,g3,…,gN-s+1},邻接矩阵序列G中的每一个元素代表一个可见图结构,由此利用可见图理论将整个时间序列映射为许多个可见图。
在状态序列G ={g1,g2,g3,…,gN-s+1} 中,在状态gi与gi+1之间存在有向的拧紧,其中1 ≤i≤N- s。为此,可以得到一个状态链,式(2):

遍历状态链,如果任意两种状态的邻接矩阵形同,则用前者状态代替后者状态。例如,如果g1=g3,则用g1替代g3,则此时状态链变为g1→g2→g1→…→gN-s+1。该遍历过程去除了状态链中重复的局部状态。将剩余的局部状态定义为网络节点,从而将原时间序列映射成为状态转移网络。
网络节点的度为局部状态gk的出现次数,网络节点之间连边的权重则是不同的局部状态之间的转移次数,节点之间连边的方向为局部状态的转移方向。在网络图中,用网络连边的粗细区分网络节点之间连边的权重。
1.2 去趋势波动分析(DFA)
去趋势波动分析(DFA)适用于分析非平稳时间序列的长期记忆。其优点是能有效去除时间序列中各阶的趋势分量,并能检测出含有噪声和多项式趋势信号的长时记忆。将DFA 应用于原始时间序列{yi},i =1,2,3,…,N的步骤如下,其中N是时间序列的长度。
(1)计算原始序列的累积偏差以获得新序列zi=,i =1,2,3,…,N,其中〈y〉 的值是整个序列的平均值,即;
(2)将综合序列zi划分为t非重叠窗口,窗口长度(数据点数)为:,其中w表示时间尺度;
(3)在每个窗口中,用二阶多项式函数拟合w个数据点zi,作为局部趋势。然后,从局部趋势中减去w个数据点,得到残差ri;
(5)本文改变了时间尺度w(1 ≤w≤N/10);
(6)在双对数坐标系下,将振幅波动F(w)绘制为时间尺度w的函数。
如果F(w)与w的关系在双对数坐标系中是线性的,F(w)(F(w)~wH)有幂律形式,其中标度指数H是线性关系的斜率。H的值量化了波动的尺度不变相关性。如果H =0.5,则与白噪声相对应的区间波动没有相关性。如果H <0.5,则波动中存在负相关,即较小的值更可能跟随较大的值,反之亦然。如果H >0.5,则波动存在正相关,即较大的值后面跟着较大的值的可能性较大,反之亦然。
2 实验与测试
2.1 汽车螺栓拧紧过程状态
根据建立状态转移网络的步骤,将汽车螺栓拧紧过程时间序列映射到网络中。网络中的每个节点表示一个状态,即图2 中的每个状态图就是图3 中的节点。在图2 中,观察到25 种状态(节点),片段长度s =5,因此本研究的状态转移网络中节点最多为25 个。注意,网络中的每个节点表示一个状态,即图2 中的每个状态是图3 中的节点。
如图3 所示,在取滑动窗口长度为s =5 时,第一组合格汽车拧紧过程序列到第五组合格汽车拧紧过程序列的状态转移网络。(a1-e1)表示由原始时间序列生成的状态转移网络;(a2-e2)表示在移除连接强度小于500 的连接后从状态转移网络获得的增强状态转移网络;(a3-e3)表示,从重组时间序列的状态转移网络中移除连接强度小于500 的连接后,获得的增强重组状态转移网络。状态转移网络中的每个节点由两个数字标识,即括号中的一个数字表示图2 中状态(或节点)的ID 号,括号左侧的另一个数字表示图1 中原始时间序列中首次出现的状态(或节点)的序列号。定向连接(箭头)表示从一个状态到另一个状态的转换。红色箭头表示权重描述转移频率的自连接,黄色框表示自连接节点。
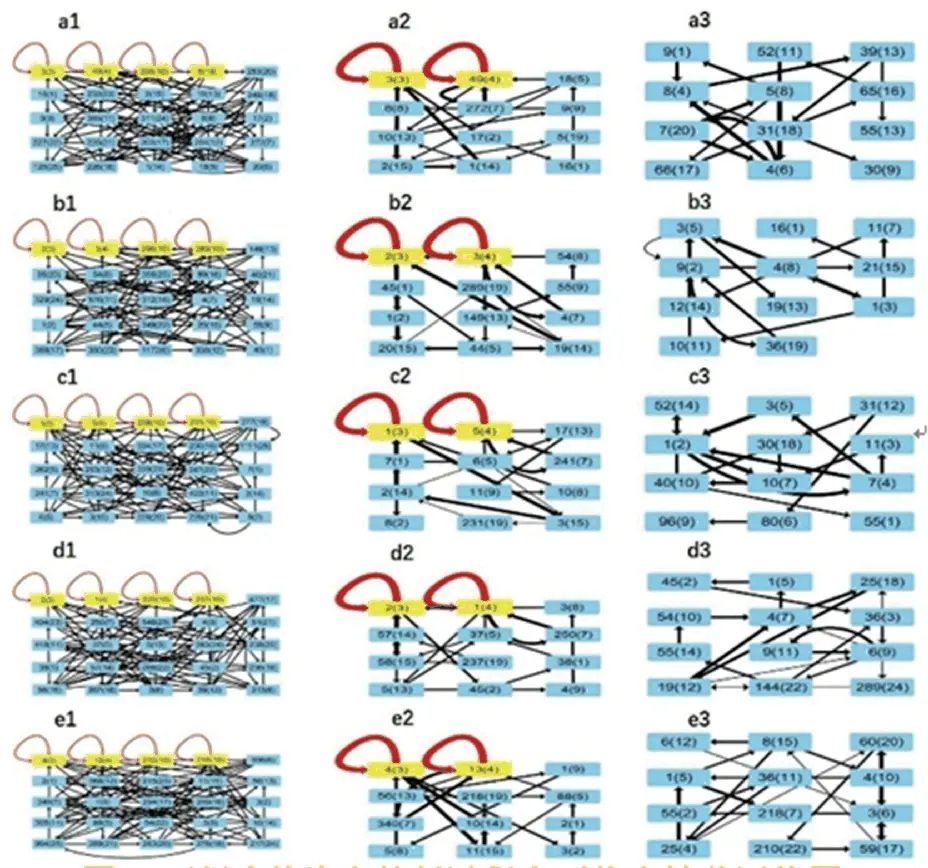
图3 5 组合格汽车拧紧过程序列状态转移网络图Fig.3 Time series state transfer network diagram of five groups of qualified automobile bolt connection process
如图4 所示,在取滑动窗口长度为s =5 时,第一组不合格汽车拧紧过程序列到第五组不合格汽车拧紧过程序列的状态转移网络。(a1-e1)表示由原始时间序列生成的状态转移网络;(a2-e2)表示在移除连接强度小于500 的连接后从状态转移网络获得的增强状态转移网络;(a3-e3)表示,从重组时间序列的状态转移网络中移除连接强度小于500 的连接后,获得的增强重组状态转移网络。状态转移网络中的每个节点由两个数字标识,即括号中的一个数字表示图2 中状态(或节点)的ID 号,括号左侧的另一个数字表示图1 中原始时间序列中首次出现的状态(或节点)的序列号。定向连接(箭头)表示从一个状态到另一个状态的转换。
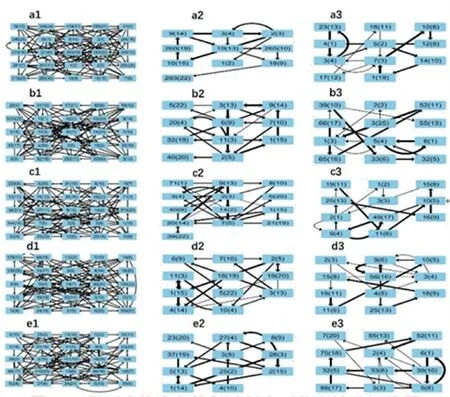
图4 5 组不合格汽车拧紧过程序列状态转移网络图Fig.4 Time series state transfer network diagram of five groups of unqualified automobile bolt connection process
如图5 所示,当滑动窗口长度为s =5 时,图为对合格汽车拧紧过程序列构造的状态转移网络和重组状态转移网络中得到了度分布、度比率和尺度指数图。(a1)-(e1)是第一组到第五组合格汽车拧紧过程序列的状态转移网络度分布。从图中可以很容易地识别出原始序列和无序序列中的关键节点;(a2)-(e2)是第一组到第五组合格汽车拧紧过程序列重组前后状态转移网络度的比值分布。从比率中可以很容易地找到关键节点;(a3)-(e3)是第一组到第五组合格汽车拧紧过程序列模体的位置时间序列标度指数,从中可以发现模体的长期记忆性。
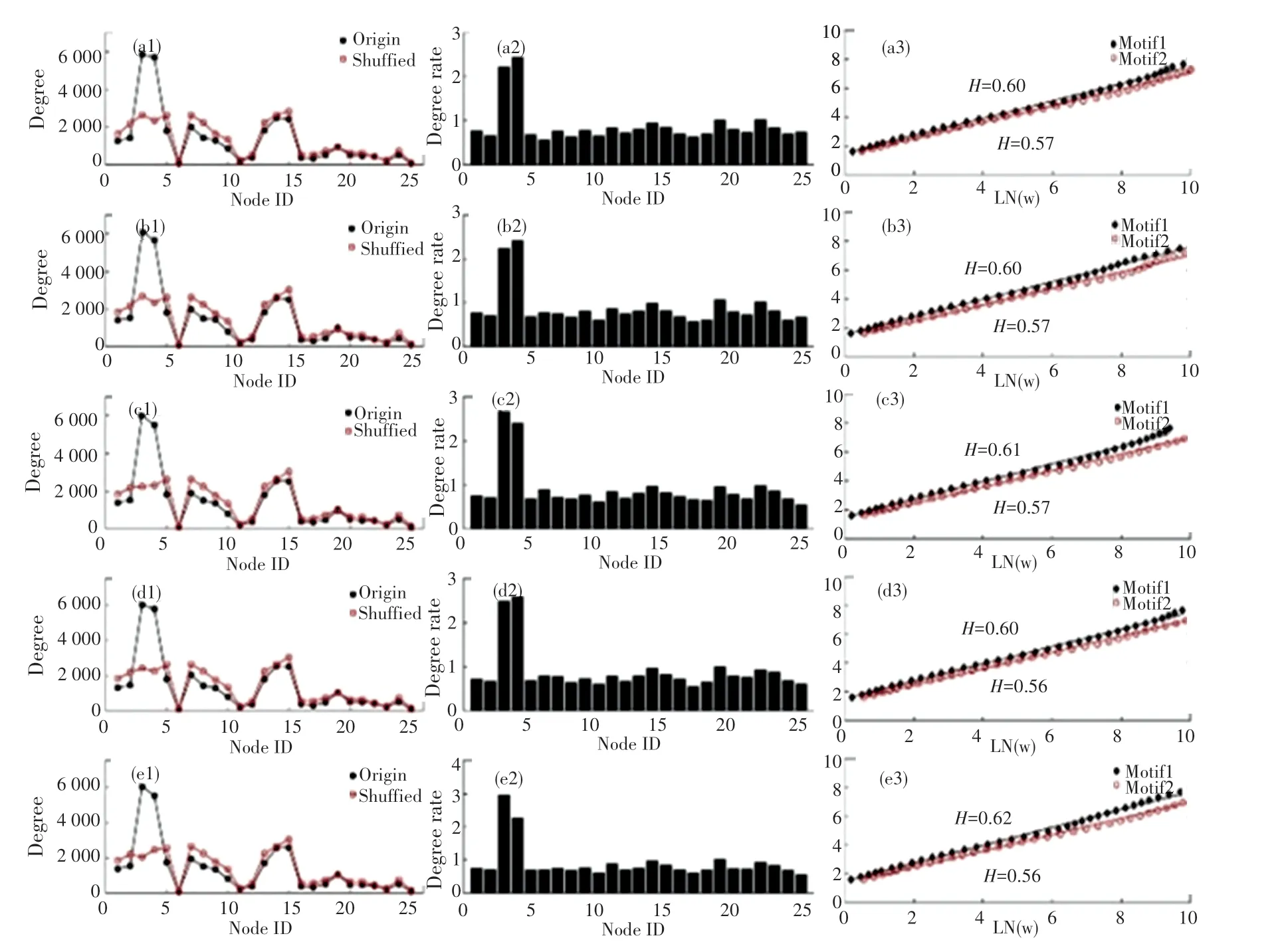
图5 5 组合格汽车拧紧过程序列状态转移网络特性分析图Fig.5 Characteristic analysis diagram of time series state transfer network of five groups of qualified automobile bolt connection process
2.2 汽车螺栓拧紧过程状态转移网络
由合格汽车拧紧过程和不合格汽车给拧紧过程的时间序列生成的状态转移网络分别如图3(a1-e1)和图4(a1-e1)所示。为了更清楚地观察网络结构,过滤掉原始状态转移网络中连接强度小于500的连接,得到图3(a2-e2)和图4(a2-e2)中的增强状态转移网络。为了进行比较,随机重组了原始合格汽车拧紧过程时间序列。删除连接强度小于500的连接后,随机时序的增强状态转移网络如图3(a3-e3)和图4(a3-e3)所示。每个节点由图3 中的两个数字标识,即括号中的数字表示图2 中状态(或节点)的ID 号,括号左侧的另一个数字表示图1 中原始时间序列中首次出现的状态(或节点)的序列号。例如,对于图3(a1)中的左上角节点20(6),“20”表示该节点第一次从图1(a)中的第20 个数据点出现,而“6”表示图2 中的第6 状态(节点)。
在状态转移网络中,自连接节点即具有从自身到自身的连接的节点,如图3(a1-e1)所示。a1 中第一组合格汽车拧紧过程序列的自连接节点分别为3(3)、49(4)、208(10)和5(19);b1 中第二组合格汽车拧紧过程序列的自连接节点分别为2(3)、3(4)、296(10)和289(19);c1 中第三组合格汽车拧紧过程序列的自连接节点分别为1(3)、5(4)、238(10)和231(19);d1 中第四组合格汽车拧紧过程序列的自连接节点分别为2(3)、1(4)、229(10)和237(19);e1 中第五组合格汽车拧紧过程序列的自连接节点分别为4(3)、13(4)、232(10)和218(19)。在增强的状态转移网络中,自连接节点也在图3(a2-e2)中可观察到,a2 中第一组合格汽车拧紧过程序列的自连接节点分别为3(3)和49(4);b2 中第二组合格汽车拧紧过程序列的自连接节点分别为2(3)和3(4);c2 中第三组合格汽车拧紧过程序列的自连接节点分别为1(3)和5(4);d2 中第四组合格汽车拧紧过程序列的自连接节点分别为2(3)和1(4);e2 中第五组合格汽车拧紧过程序列的自连接节点分别为4(3)和13(4)。在图3(a1-e1)中,虽然不同合格汽车拧紧过程序列中的自连接节点对应于原始时间序列首次出现的不同位置,但自连接节点的对应状态是相同的(自连接节点对应的括号外的数字是不同的,括号内的数字相同)。在增强状态转移网络中,合格汽车拧紧过程序列的不同组之间的自连接节点数目也是相同的;在图3(a2-e2)中,每个组的自连接节点数目减少到2 个。作为比较,本文提出的增强型重组状态转移网络中不存在自连接节点,如图3(a3-e3)所示。
此外,本文还研究了图3(a2-e2)中增强状态转移网络中自连接强度的值。具体地,对于合格汽车拧紧过程的第一组序列中的节点3(3)和49(4),状态转移网络中的连接强度分别为3 240 和3 239;对于合格汽车拧紧过程的第二组序列中的节点2(3)和节点3(4),状态转移网络中的连接强度分别为3 204和3 224;对于合格汽车拧紧过程的第三组序列中的节点1(3)和5(4),状态转移网络中的连接强度分别为3 149 和3 119;对于合格汽车拧紧过程的第四组序列中的节点3(3)和49(4),状态转移网络中的连接强度分别为3 204 和3 224;对于合格汽车拧紧过程的第五组序列中的节点4(3)和节点13(4),状态转移网络中的连接强度分别为3 166 和3 165。
与每组合格汽车拧紧过程序列相反,在图4 中的每个不合格汽车拧紧过程序列的状态转移网络、增强状态转移网络和增强重组状态转移网络中均未观察到自连接节点。这种自连接节点的差异表明合格汽车拧紧过程序列和不合格汽车拧紧过程序列之间的网络拓扑结构不同,并且暗示合格汽车拧紧过程序列和不合格汽车拧紧过程序列之间的动态行为也不同。
2.3 状态转移网络的节点度
由5 组合格汽车拧紧过程序列和随机重组时间序列生成的每个节点的度,如图5(a1)-(e1)所示;5 组合格汽车拧紧过程序列节点度与随机重组时间序列节点度的比率,如图5(a2)-(e2)所示。如果状态转移网络中关键节点的节点度明显大于无序状态转移网络中关键节点的节点度,则该节点称为模体,可以作为状态转移网络的全局代表。根据模体的定义,可以找到5 组合格汽车拧紧过程序列的模体。第一组合格汽车拧紧过程序列的状态转移网络中的模体1 和模体2,对应节点为3(3)和49(4);第二组合格汽车拧紧过程序列的状态转移网络中的模体1 和模体2,对应的节点分别为状态2(3)和状态3(4);第三组合格汽车拧紧过程序列的状态转移网络中的模体1 和模体2,对应的节点为1(3)和5(4);第四组合格汽车拧紧过程序列的状态转移网络中的模体1 和模体2,对应节点分别为2(3)和1(4);第五组合格汽车拧紧过程序列的状态转移网络中的模体1 和模体2,对应的节点为4(3)和13(4)。可见图显示5 组合格汽车拧紧过程序列对应的可见图结构(3)和(4)为模体,度值最大。可见图结构(3)和(4)在合格汽车拧紧过程序列中具有重要意义,如图5(a2)-(e2)。
为了研究模体在合格汽车拧紧过程序列中是否随机出现,提取了合格汽车拧紧过程序列中状态3或状态4 的位置,得到了对应的位置时间序列,采用去趋势波动分析方法计算Hurst 指数H值。第一组合格汽车拧紧过程序列的模体1 和模体2 对应的H值分别为0.60 和0.57;第二组合格汽车拧紧过程序列的模体1 和模体2 对应的H值分别为0.60 和0.57;第三组合格汽车拧紧过程序列的模体1 和模体2 对应的H值分别为0.61 和0.57;第四组合格汽车拧紧过程序列的模体1 和模体2 对应的H值分别为0.60 和0.56;第五组合格汽车拧紧过程序列的模体1 和模体2 对应的H值分别为0.62 和0.56。五组合格汽车拧紧过程序列对应的模体的H值均在0.6 左右,说明模体不是随机出现的。
3 结束语
本文通过可见图方法将5 组合格汽车拧紧过程序列与5 组不合格汽车拧紧过程序列映射到状态转移网络,探究了汽车拧紧过程的动态机制。经研究发现5 组合格汽车拧紧过程序列产生的状态转移网络在网络特性上趋于一致,并且5 组合格汽车拧紧过程序列具有相同的模体。而5 组不合格汽车拧紧过程序列产生的状态转移网络在网络特征上没有相似性,也没有模体的出现。
具体而言,(3)、(4)、(10)、(19)的自连接节点出现在5 组合格汽车拧紧过程序列的原始状态网络(图3(a1)-(e1))中,并且节点(3)和(4)经Hurst指数验证为5 组序列的模体。不合格汽车拧紧过程序列的原始状态转移网络中没有模体,这意味着5组不合格汽车拧紧过程序列在拧紧过程中表现出随机性,序列之间没有共同特征。为此,本文使用的状态转移网络的方法有效的验证了合格序列和不合格序列之间存在的差异。
实验结果表明:在可见图结构(3)和(4)中,5 组合格汽车拧紧过程序列中的出现最显著,并且出现明显的非偶然强自连接节点(3)和(4),这两种状态的标度指数均大于0.5,证明该时间序列具有长期记忆性,说明合格汽车拧紧过程序列具有长期记忆性。
由于合格汽车拧紧过程序列的分形性质,在未来的研究中,将进一步探索合格汽车拧紧过程序列在其他时间尺度上的运行规律,希望能揭示更深刻的时间序列运行规律。

