基于细胞型膜计算的煤矿巡检无人直升机姿态控制
许家昌, 黄友锐, 李虹金, 刘瑜, 韩涛
(1.安徽理工大学 计算机科学与工程学院,安徽 淮南 232001;2.安徽理工大学 电气与信息工程学院,安徽 淮南 232001;3.大连理工大学 生物医学工程学院,辽宁 大连 116000;4.安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南 232001)
0 引言
煤矿智能开采过程中[1],智能巡检(瓦斯浓度、管线及灾后搜救等)在煤矿灾害防控体系中占据重要地位,机器人在井下巡检具备一定的优势,面临大的障碍物时,在可通过性方面,无人直升机更具优势,如何让无人直升机快速高效完成巡检任务,姿态控制是关键。
近年来,关于无人直升机姿态控制[2-3]的研究取得了许多成果。文献[4]建立了无人直升机线性模型,设计实现了姿态跟踪控制器,通过仿真及实验证明了控制器设计的有效性。文献[5]采用反步法设计了无人直升机飞行控制律,利用自适应方法实现了系统参数在线估计,达到了对直升机姿态控制的目的。文献[6]利用反步法与神经网络相结合,实现了无人直升机的定位,一定程度上提高了无人直升机的飞行性能。文献[7]通过设计无人直升机非线性控制器,实现了无人直升机的姿态控制及位置跟踪。文献[8]利用非线性控制算法实现了无人直升机的自适应控制性能。文献[9]利用模糊控制理论,实现了无人直升机的控制器设计,提高了无人直升机的姿态控制性能。文献[10]利用神经网络和强化学习设计无人直升机的姿态控制器,通过实验验证了算法的有效性。文献[11]实现了复杂环境下的多机姿态控制。现有无人直升机姿态控制大多以线性和非线性算法为主,在控制效果上均表现出了较好的性能,但是伴随应用场景的变化,扰动也随之变化,导致无人直升机姿态波动幅度和误差变大。膜计算[12]作为受细胞组织机理启发而产生的计算模型,具有分布式、并行计算的优势,正朝着优化控制领域进行突破性延伸,成为当前的研究热点。因此,本文引入细胞型膜计算实现对煤矿巡检无人直升机姿态的优化控制。通过建立无人直升机动力学模型,推导出无人直升机姿态动力学模型,构建了无人直升机细胞型膜系统,以此作为无人直升机运动姿态控制的依据,通过构建无人直升机姿态膜控制器(Membrane Controller,MC)完成对无人直升机姿态的控制。
1 无人直升机姿态动力学模型
建立正确的机体坐标系与地面坐标系之间的换算关系是表征无人直升机运动状态的前提。为实现无人直升机姿态控制,需要控制姿态角(偏航角Φ、俯仰角θ、滚转角ψ)。
由于井下环境复杂,本文只考虑无人直升机在主旋翼和尾旋翼作用下的运动和动力学特性。无人直升机动力学模型由无人直升机本体动力学方程、旋翼动力学方程和角速度控制器3个部分构成,如图1所示,其中uped,ucol,ulat,ulon分别为方向舵机、主旋翼舵机、副翼舵机和俯仰舵机的输入,FB为外作用力,τB为扭矩向量。

图1 无人直升机动力学模型
作用于无人直升机上的力和力矩决定着无人直升机飞行性能的优劣,通过坐标系的变换确定无人直升机的位置和方向,从而提供准确的姿态和平移运动信息。假设地面坐标系下的线速度和角速度坐标向量分别为υ和ω, 则υ和ω在机体坐标系中表示为[13]
υ=oBvX+jBvY+lBvZ
(1)
ω=oBwX+jBwY+lBwZ
(2)
式中:oB,jB,lB分别为X,Y,Z轴的单位向量;vX,vY,vZ分别为X,Y,Z轴线速度;wX,wY,wZ分别为X,Y,Z轴角速度。
利用旋转矩阵R对地面坐标系下无人直升机位姿和平移运动推理,结合R的导数,可得无人直升机动力学方程:
(3)
式中I为单位矩阵。
考虑无人直升机负载,本文忽略尾翼推力对无人直升机的影响,即无人直升机仅受主旋翼和重力作用。
(4)
式中:G为无人直升机所受重力;TM为主旋翼作用力。
无人直升机姿态动力学模型为
(5)
式中:ωB为机体角速度向量;QM为反作用扭矩向量;(xc,yc,zc)为主旋翼位置向量;D为旋翼彀的刚度;a为正增益;(xh,0,zh)为尾旋翼位置向量;σ为控制姿态稳定性的输入向量。
2 细胞型膜系统
细胞型膜系统是一种具有分层膜结构分布式并行计算模型,考虑无人直升机参数的特性,定义度为s(s≥1)的数值膜系统[14]。
Π={s,H,μ,(V1,P1,V1(0)),…,(Vs,Ps,Vs(0))}
(6)
式中:H为膜标记集合;μ为包含度为s的膜结构;Vi为膜结构区域i内的1组变量,1≤i≤s;Vi(0)为Vi的初始值;Pi为膜结构区域i内的1组规则,包括值的产生规则和分配规则。
系统中第t条规则可定义为
Pt,i={ft,i(d1,i,d2,i,…,dk,i),
λt,1|g1+λt,2|g2+…+λt,n|gn}
(7)
式中:ft,i(d1,i,d2,i,…,dk,i)为膜结构区域i内值的产生规则,dk,i为膜结构区域i内第k个随机变量;λt,1|g1+λt,2|g2+…+λt,n|gn为第n个值的第t条分配规则,λt,1—λt,n为膜结构区域i内第n个值的分配比例系数,g1—gn为膜结构区域i内第n个值的分配对象。
当值的产生规则计算出值f时,该值除以分配比例系数λt,1—λt,n之和,得到膜的值。如果在膜的值分配过程中存在相同变量,把计算得到膜的值分配给每个变量,且把计算累加值作为变量的最终值。
3 无人直升机姿态MC
以姿态角振幅的大小和姿态控制误差表征无人直升机姿态MC稳定性和有效性。
设定控制率规则按照顺序执行,设定完整的无人直升机姿态MC计算周期需循环3次完成。假设eΦ为偏航角误差,则偏航角误差动力学方程为
(8)
式中b为偏航角速度伪控制矩阵。
(9)
式中:r为伪控制调节系数;αr为基于r的调节矩阵;ew为角速度误差。
式(9)去除非线性项后,可得
(10)
结合式(5),推导出角速度误差。
(11)
式中A为正增益对角矩阵。
同理,考虑正交向量约束的局限性,角速度伪控制下的方向误差动力学方程为
(12)
式中:[β1β2]为正交调节矩阵;ep为p的误差;Z0(θ)为正交向量。
式(9)、式(11)和式(12)构成无人直升机姿态误差方程。
4 实验验证
利用设计的细胞型膜系统及机载计算机与激光雷达、深度相机等传感器搭建实验平台,实验平台软硬件参数见文献[15]。为验证无人直升机姿态MC的性能,将MC分别与线性反馈控制器(Linear Feedback Controller,LFC)、传统滑膜控制器(Traditional Synovial Controller,TSC)进行比较。
4.1 地面上空飞行实验
实验所需的各种传感器均采用双面轻泡沫粘胶固定,以减小无人直升机飞行过程中因本体振动而出现过大的数据误差,起飞前调试并确保各姿态角与控制量之间呈同向关系。为保证实验结果更加合理可靠,地面上空飞行路线距离墙体1.5 m,距离地面高度为3.5 m。
实验开始时控制无人直升机达到平稳状态,之后将飞行状态转换到自动飞行状态,得到地面上空无人直升机姿态角随时间t变化曲线,如图2和图3所示。
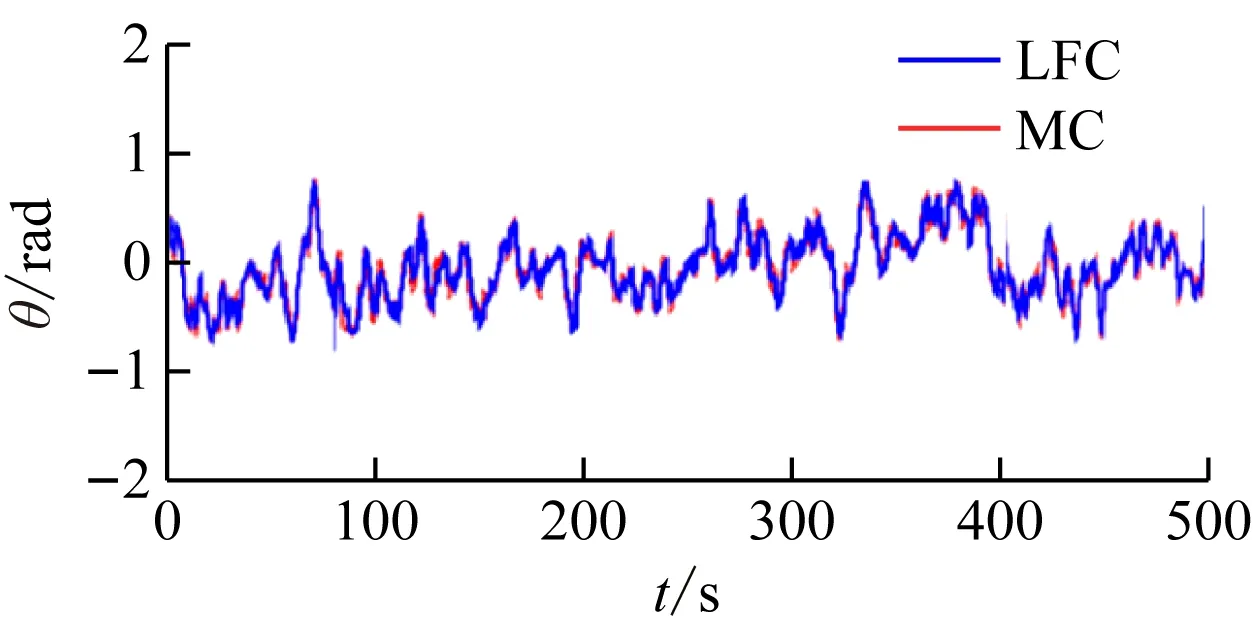
(a)俯仰角随时间变化
从图2和图3可看出,无人直升机在地面上空飞行过程中,在MC、LFC和TSC下均完成了对无人直升机姿态的控制,即姿态角幅度均得到了有效控制,达到了相对稳定状态;MC姿态角控制在-0.8~0.8 rad范围内,姿态角振荡幅度小于TSC和LFC下姿态角振荡幅度。
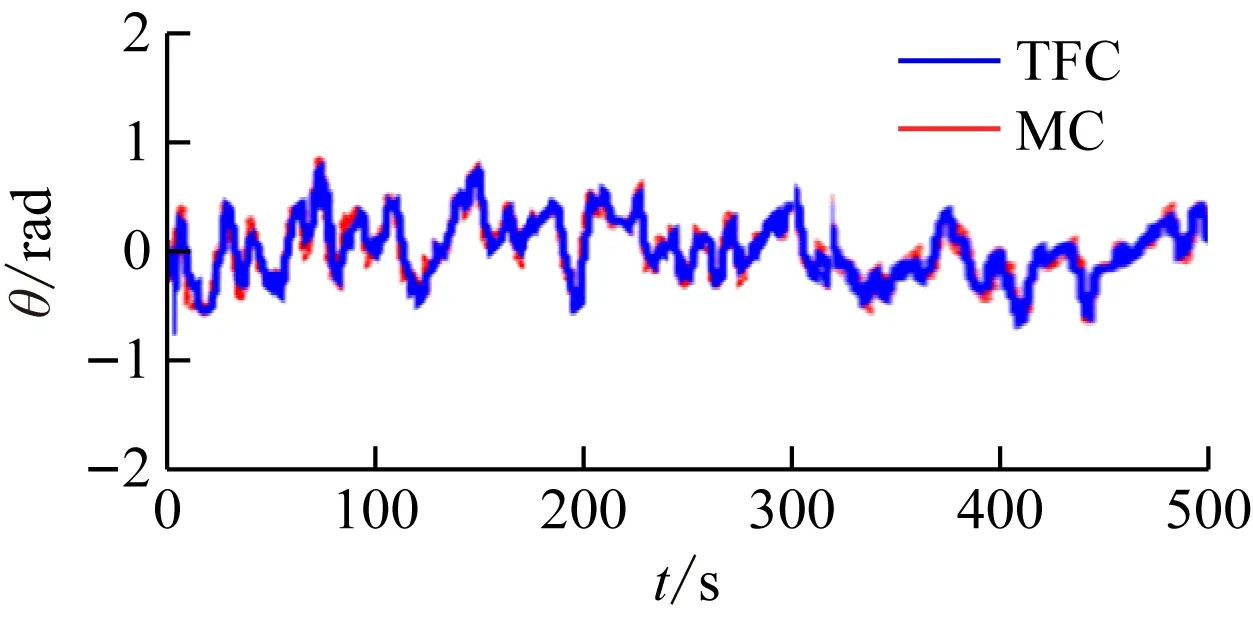
(a)俯仰角随时间变化
4.2 煤矿巷道飞行实验
受无人直升机电源防爆等限制,在模拟巷道(风速控制在4 m/s)进行实验。模拟巷道无人直升机姿态角随时间变化曲线如图4和图5所示。
从图4和图5可看出,无人直升机在模拟巷道飞行过程中,MC、LFC和TSC下无人直升机姿态角均没有出现大幅波动,姿态角振荡幅度为-2~2 rad;MC下姿态角振荡幅度最小,为-1.8~2.0 rad范围之内,且波动频率变小。

(a)偏航角随时间变化
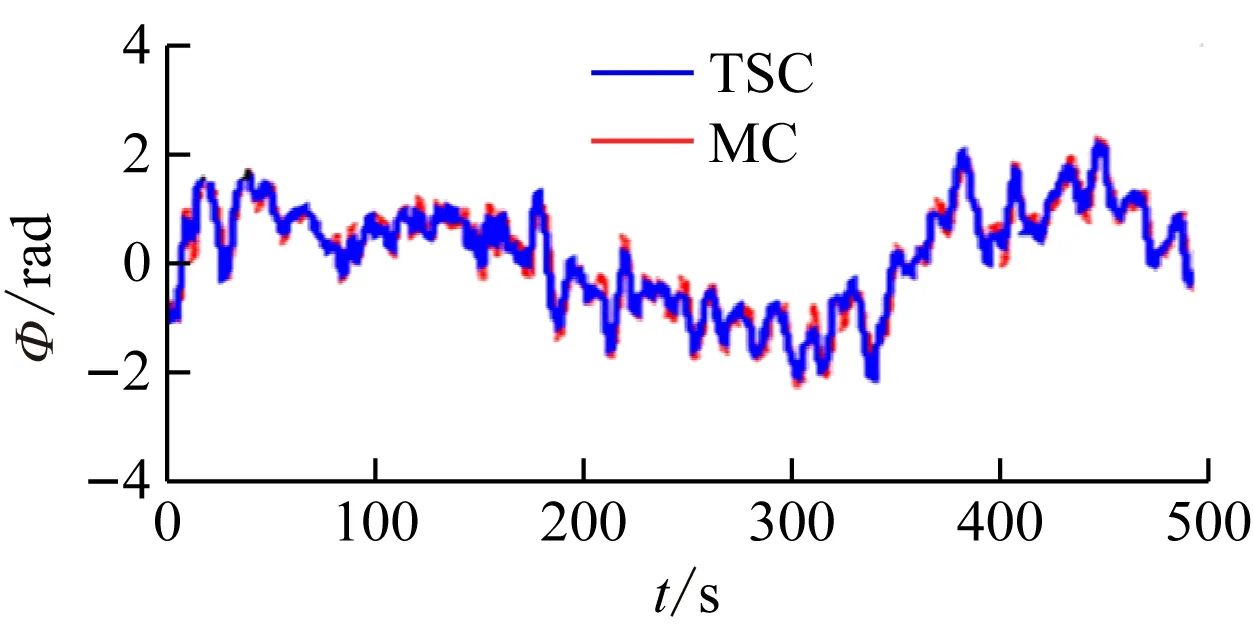
(a)偏航角随时间变化
4.3 姿态角误差
根据实验过程中得到的数据,TSC、LFC和MC下姿态角误差见表1,可看出MC下姿态角误差小于TSC和LFC下姿态角误差。

表1 姿态角误差
5 结论
(1)根据无人直升机动力学模型构建了无人直升机姿态动力学模型,设计了细胞型膜系统和无人直升机MC。
(2)在地面上空环境,MC下的姿态角控制在-0.8~0.8 rad,姿态角振荡幅度小于TSC和LFC下的姿态角振荡幅度;在模拟巷道环境,MC下的姿态角控制在-1.8~2.0 rad,波动频率小;MC下的姿态角误差小于TSC和LFC下的姿态角误差。
(3)由于实际工矿巷道下灰尘、温度、湿度与模拟巷道存在一定的差异性,可能导致实验结果与实际工矿巷道下的实验结果存在一定差异,通过地面上空和模拟巷道实验证明了MC的优越性能,后续在符合煤矿安全规程的前提下,继续进行实际工矿下的现场实验。

