扰动环境下火星精确着陆自主轨迹规划方法

邓云山,夏元清,*,孙中奇,沈刚辉

1. 北京理工大学 自动化学院,北京 100081

2. 复杂系统智能控制与决策国家重点实验室,北京 100081

未来的火星探测任务要求探测器具有精确着陆的能力[1-2]。探测器需要经历大气进入(Entry)、下降(Descent)以及最终着陆(Landing)过程(也称为EDL过程)[3],其中下降段包含伞降段与动力下降段(Powered-Descent Guidance, PDG),而动力下降段的轨迹规划是动力下降段制导控制问题中的重要研究内容。因此提高轨迹规划速度,使着陆器在线实时生成着陆轨迹对提高着陆器的生存能力和着陆精度具有重要意义[4]。

着陆器抛弃降落伞后,探测器进入动力下降段,需要利用火箭反推技术,进行姿态调整及障碍规避,最终悬停于预期着陆点正上方,释放火星车[3]。整个过程需要满足最大、最小推力约束,最小下降角等多个约束条件。文献[5]将能量最优动力下降段制导问题转化为二阶锥优化问题。在给定精度下,此类型优化问题可使用内点法在多项式时间内求解[6-8]。文献[9]在文献[5]的基础上,针对着陆点不可达问题,提出了最小着陆误差的轨迹规划算法,首先求解最小着陆误差问题得到距离预期着陆点最小距离的可降落区域,然后在该降落区域内求解能量最优规划问题。文献[4] 将能量最优下降问题转化为有限个推力为常值的分段函数,给出了每段内微分方程的解析表达式,并利用序列二次规划(Sequential Quadratic Program,SQP)算法对待求参数进行迭代求解。这种方法在一定程度上提高了计算效率。文献[10]基于凸优化方法研究了给定着陆精度下的约束可控集与约束可达集,通过对数据集的量化,评估给定着陆器着陆的可行性。文献[11]结合凸优化方法与伪谱法,对比了Radau伪谱法、Lobatto伪谱法与标准凸优化方法的求解结果,结果表明,结合伪谱法的求解精度较高,但求解时间增加,在少量谱点情况下具有工程实用性。文献[12] 研究了不规则小行星动力着陆轨迹规划问题,考虑引力模型,对固定时间着陆问题进行了无损凸化。

上述方法只考虑了固定终端问题,实际问题中,终端时间也为未知变量。文献[5,9]采用外嵌黄金分割法(Golden Search Procedure, GSP)进行终端时间的线性搜索,这种方法可以解决终端时间自由问题,但是以牺牲计算时间为代价。文献[13]考虑阻力模型,针对终端时间自由问题,对非线性动力学直接进行线性化,初步解决了终端时间自由轨迹规划问题。文献[14]针对直接线性化处理中,终端时间初值的估计不准确时,问题可能在迭代前几次不可行进而造成求解失败的情况,选择对高度变量进行求导并设计高度离散方法。所设计的高度离散方法可尽可能使对应离散点时间间隔相同,但无法保证统一的时间步长,同时无法对扰动进行建模。

针对扰动环境,常采用2种方式进行克服：① 采 用预先规划加反馈跟踪控制的思想进行;② 在 下降过程中不断进行重规划。其中,前者在扰动作用下,规划轨迹在实际中可能不可行。后者虽然从规划层次上考虑了扰动,相比于前者具由更强的鲁棒性,但重规划问题的可行性无法从理论上进行论证,可能出现重规划不可行的情况。值得说明的是,文献[15]结合本质鲁棒MPC(Model Predict Control)思想,提出了保证可行性的重规划问题,巧妙解决了重规划不可行问题。但其未考虑2次重规划间隔间的抗扰,抗扰能力与2次重规划间隔相关,重规划频率越高,抗扰能力越强,但依靠高频率优化进行制导,会出现重规划频率与计算能力的矛盾。增加内环反馈控制后可降低重规划频率,但同时需要考虑规划问题与内环控制的耦合。本文针对终端自由扰动环境下火星着陆动力下降段轨迹规划问题,结合Tube-MPC思想[16]设计反馈控制律,考虑规划问题与内环控制的耦合,提出了鲁棒意义下的自主轨迹规划框架并分析了重规划问题的可行性。外环采用序列凸优化(Sequential Convex Programming, SCP)方法进行求解,并分析了求解结果的最优性；内环采用反馈控制律直接控制,进一步提高抗扰性能。同时给出了重规划问题可行的必要条件,为实际工程应用提供参考。

1 问题描述

火星着陆动力下降段任务高度在距离火星5 km 高度内[5],重力加速度可视为常数。由于火星大气稀薄,在动力下降段最优轨迹规划中通常将气动力等其他力的作用视作扰动。

动力下降段开始前,通过伞降段充分减速,此时着陆器速度量级为100 m/s。动力下降段开始时,着陆器与降落伞分离,点燃火箭反推装置,从距离火星表面约1.5 km开始下降到期望着陆点正上方20 m处进行悬停。

动力下降段自主轨迹规划在初始时刻进行一次规划,随着着陆器的下降进行实时重规划。整个过程火箭反推推力需要位于允许最小推力与允许最大推力之间,着陆轨迹需要避免下降过程中与火星表面发生碰撞,并尽可能使整个过程能耗最小。

1.1 着陆器动力学

以期望着陆点为原心,X轴沿火星经线指向东方,Z轴竖直向上,Y轴满足右手定则,建立火星表面固连坐标系。着陆器动力学为

(1)

(2)

1.2 耗能最优

能耗最优的需求可描述为动力下降任务开始(0时刻)到结束(tf时刻),所消耗燃料的质量最小,也即最大化任务结束时刻着陆器质量与任务初始时刻着陆器质量的差：

maxm(tf)-m(0)

(3)

同时,由于着陆器质量满足式(2),因此上述指标等价于最小化任务过程中推力大小的积分：

(4)

1.3 过程约束

下降过程中,火箭发动机推力大小处于最小允许推力ρmin与最大允许推力ρmax之间,即

(5)

同时为避免与火星表面的山峰状障碍物相撞,下降轨迹需要满足滑降约束：

r(t)∈X

(6)

X={r∈R3:

(7)

式中:rX、rY、rZ分别为着陆器位置r沿坐标轴方向的投影分量;rfX、rfY、rfZ分别为预期悬停位置rf沿坐标轴方向的投影分量;γ为一给定角度常数。

滑降约束几何含义为着陆器下降轨迹位于以预期悬停位置为顶点,开口方向平行于Z轴向上的圆锥型区域内,属于二阶锥约束。

1.4 起始、终端约束

任务起始于着陆器满载燃料的质量mwet,初始位置r0与速度v0：

(8)

要求终止时刻着陆器的质量大于燃料耗尽时着陆器的质量mdry,且终止位置、速度达到预期悬停位置rf与速度vf：

(9)

1.5 无扰燃料最优轨迹预规划问题

着陆过程可描述为以能量最优为指标的最优控制问题,需要满足着陆器动力学约束、状态约束、控制约束。

燃料最优火星着陆动力下降段轨迹规划问题以下降过程中消耗燃料最少为性能指标,表示为[9]

P1(非凸燃料最优问题)：

(10)

s.t. 式(1),式(2),式(5),式(6),式(8),式(9)

其中:式(1)～式(2)为非线性等式约束,式(5)为非凸不等式约束。

文献[5]与文献[9]对优化问题P1进行凸化处理与变量替换,通过引入新控制变量Γ,对P1进行无损凸化,并给出了无损凸化的充分条件。并通过如下变量替换,得到问题P2。

(11)

(12)

z(t)=lnm(t)

(13)

P2(松弛燃料最优问题)：

(14)

s.t.

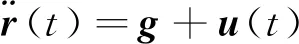
(15)

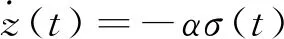
(16)

(17)

0≤ρmine-z(t)≤σ(t)≤ρmaxe-z(t)

(18)

r(t)∈X

(19)

(20)

引入新变量并进行变量替换后,动力学约束式(1)变为线性形式如式(15)所示。

2 扰动环境下轨迹重规划

实际下降过程中,由于受以气动扰动为主的扰动影响,预先规划的轨迹在实际下降过程中可能不可行,因此需要实时进行重规划,克服扰动的影响。对于重规划问题,本节将分析其可行性,并构造出重规划问题的可行解。

首先,给出扰动环境下的动力学模型,针对线性反馈控制律,参考Tube鲁棒思想[16],提出扰动环境下的轨迹重规划优化问题。其次,证明重规划问题的可行性。最后,提出扰动环境下火星着陆轨迹规划架构。

2.1 扰动环境下的轨迹重规划优化模型

由于火星大气启动参数难以在着陆前进行精确测量,因此在已处理动力学模型式(15)的基础上建立扰动动力学模型：

(21)

式中:dp(t)为火星大气等客观因素引起的扰动,扰动具有上界|dp(t)|≤η, |·|表示向量按位取绝对值。记m⊙n为2个向量按位相乘。tk时刻扰动环境下重规划问题如下。

P3(k)(扰动环境下重规划问题)：

(22)

s.t.

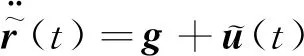
(23)

(24)

(25)

(26)

r(t)∈X

(27)

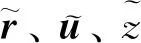
考虑单一方向上的特征根分布情况,特征方程在复平面左半平面内有2个共轭复根λ1=λRe+λImi,λ2=λRe-λImi(λRe<0,λIm≥0)时,rtube=η(2λIm-λRe)/(λImλ1λ2),vtube=η/λIm；当特征方程在复平面左半平面内有2个不同实根λ1≠λ2时,有rtube=η/(λ1λ2),vtube=η/|λ1-λ2|;当特征方程在复平面左半平面内有两相同实根λ1=λ2=λ时,rtube=2η/λ2,vtube=-η/eλ,e为自然常数。

注意,重规划问题P3(k)的初始状态被作为一个决策变量,实际控制量采用线性反馈形式进行控制,控制律如下：

(28)

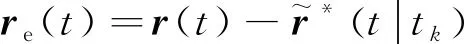
事实上,预先规划的本质是开环的,无法从规划的角度上考虑实时扰动；重规划对下降过程中的轨迹进行修正,可以达到更优的性能。重规划中,若不对优化问题进行处理,则无法保证问题的可行性。

2.2 重规划可行性分析

与直接以P2问题进行重规划相比,P3(k)可以在理论上保证重规划问题的可行性,并可以根据上次规划结果构造出下次重规划问题的可行解。本节将在连续时间情况下,分析重规划问题的可行性,首先给出引理1。

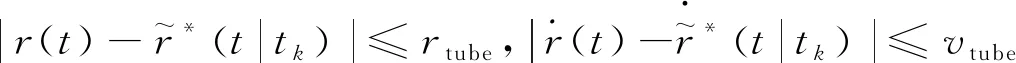
1) 单一方向上特征根λ1、λ2为不相等共轭复根,即λ1=λRe+λImi,λ2=λRe-λImi(λRe<0,λIm>0)时:

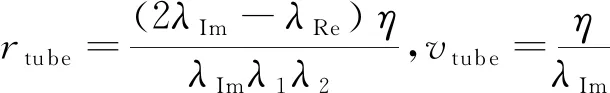
(29)

2) 单一方向上特征根为不相等实根,即λ1≠λ2时:

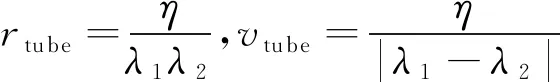
(30)

3) 单一方向上特征根为相等实根,即λ1=λ2=λ时:

(31)

证明：考虑单个方向的误差状态,由于

(32)

代入线性反馈控制律得：

(33)

即误差状态方程为

(34)

下面就特征根进行分类讨论：

1) 当特征根λ1、λ2为不相等共轭复根时：

C1eλ1t+C2eλ2t

(35)

有

(36)

第1项展开为

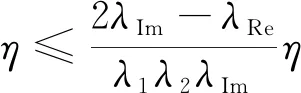
(37)

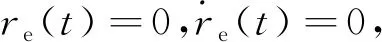
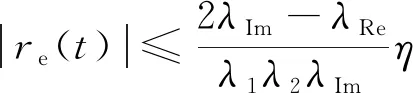
(38)

对(35)式求导有

(39)

放缩得到

(40)

2) 当特征根λ1、λ2为两不等的实根时,由于：

(41)

因此式(36)可放缩为

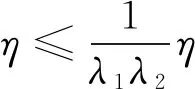
(42)

式(40)变为

(43)

3) 当特征根λ1=λ2=λ<0为相等的实根时：

(44)

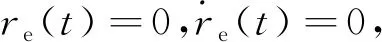
(45)

求导可得(λt-1)eλt单调递增,因此有

-1≤(λt-1)eλt≤0

(46)

所以

(47)

对式(44)求导得

(48)

有

(49)

求导可得teλt在t=-1/λ时取最大值,结合teλt≥0可得

(50)

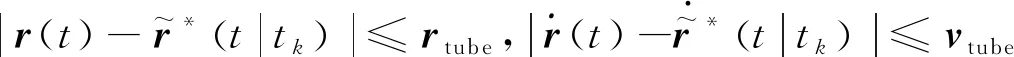
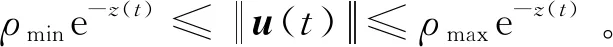
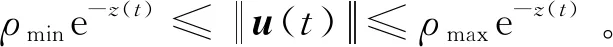
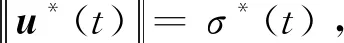
(51)

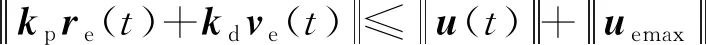
(52)

(53)

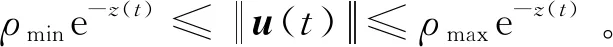
下面对重规划问题P3(k)进行可行性分析。

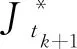
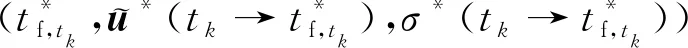
不难验证部分解满足P3(k+1)问题的式(6),式(20),式(23)～(26)约束。

考察部分解的初始状态,由引理1可知：

(54)

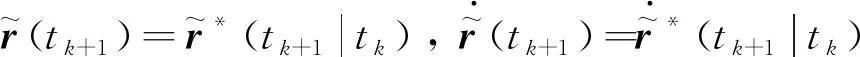
由于重归化问题可行性需求,需要对预规划问题P2的约束式(18)进行修正,用P3(k)中的约束式(26)替代,得到修正后的预规划问题P4。

通过数学归纳法可得,对于连续时间系统,当修正后的预规划问题P4可行时,后续重规划问题可行,且最优性更强。下面给出预规划问题P4的必要性条件,为参数筛选提供参考。

定理2当预规划问题P4可行时,控制参数满足如下不等式：

(55)

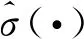
(56)

移项并代入uemax=kp⊙rtube+kd⊙vtube得：

(57)

依据式(13)进行变量反代换得：

(58)

□

其逆否命题可作为控制参数初步筛选的依据：满足式(59)的参数一定使预规划问题P4不可行。

(59)

注意,满足不等式(55)的参数不一定使问题P4可行。

2.3 扰动环境燃料最优轨迹规划算法框架

扰动环境燃料最优轨迹规划框架如算法1所示。

算法1 扰动环境燃料最优轨迹规划方法1. 初始化:k=1, t=t02. 在t0时刻检测着陆器实际状态,构建并求解修正轨迹预规划问题P4,获得最优控制序列;3. 根据线性反馈控制律式(28)计算实际控制信号,对着陆器进行实时控制;4. 检测当前时刻t是否满足重规划触发条件,若满足,进入步骤5;若不满足,返回步骤3;5. 令tk=t,构建并求解轨迹重规划问题P3(k),获得最优控制序列,k=k+1;6. 检测着陆任务是否完成:若未完成,返回步骤3;若完成,则退出算法。

重规划触发条件可以根据任务实际需求进行设置,可以设置为一定时间间隔Δt后自动开始重规划,也可设置为误差相关的事件触发条件。

注意,若直接在P2中代入当前状态信息进行重规划,难以构造可行解,并可能出现优化不收敛的情况,这极大降低了重规划的可靠性。但对于问题P3(k),可以根据上次规划结果直接构造重规划问题可行解,当求解器因为其他原因求解失败时,可依据上次规划结果构造可行解,直至某次重规划成功。同时,可设计事件触发重规划条件,进一步降低不必要的计算量。

3 终端时刻自由

对于终端时刻固定问题而言,P3(k)与P4可经过线性化、离散化转化为二阶锥优化问题,现有求解器可在多项式时间内进行求解。对于终端时刻自由问题,P3(k)与P4中的动力学约束为非线性约束,本节将以P4为例,对飞行时域进行映射,进一步将问题凸化为有限维二阶锥优化问题。

3.1 飞行时域映射

P4中,由于终端时刻tf是未知量,因此将飞行时域[0,tf]映射到区间[0,1],有：

(60)

(61)

进而问题转化为P5(注意,此时求导运算为对τt求导)。

P5：

(62)

s.t.

(63)

(64)

(65)

(66)

(67)

(68)

r(τt)∈X

(69)

z(0)=lnmwet,r(0)=r0,v(0)=v0

(70)

z(1)≥lnmdry,r(1)=rf,v(1)=vf

(71)

其中,目标函数式(62)、动力学约束式(63)～式(65) 均为非线性形式。

3.2 目标函数凸化

非线性目标函数可转化为线性目标函数外加一个非线性不等式约束的形式：

(72)

式中：δ(·)为中间变量。

3.3 离散化

在时域[0,1]上,使用欧拉法将动力学离散为N段,得到P6。

P6：

(73)

s.t.

(74)

(75)

zi-zi-1=-ασitf

(76)

(77)

(78)

(79)

σitf≤δi

(80)

ri=0,ri=1,…,ri=N∈X

(81)

zi=0=lnmwet,ri=0=r0,vi=0=v0

(82)

zi=N≥lnmdry,ri=N=rf,vi=N=vf

(83)

P6包含非线性等式约束式(74)～式(76)以及非凸不等式约束式(78)～式(80),其余约束为二阶锥形式(包含半平面)。因此可写为标准形式P6*。

P6*：

(84)

s.t.

Ay-b≥κ0

(85)

Cy-d=0

(86)

gi(y)≤0

(87)

hj(y)=0

(88)

式中：y为优化变量；c为式(73)转化为标准形式后的加权系数；符号≥κ表示在二阶锥κ中的广义不等式。式(85)表示旋转二次锥约束[17],相关参数A、b、κ由约束式(77)和式(81)整理得到；C、d由线性等式约束式(82)～式(83)整理得到；式(87) 为非线性不等式约束的一般形式,函数gi(y)由约束式(78)～式(80)整理得到；式(88)为非线性等式约束,函数hj(y)由约束式(74)～式(76) 整理得到。

3.4 线性近似

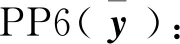
s.t.

(89)

(90)

(91)

(92)

(93)

(94)

ri=0,ri=1,…,ri=N∈X

zi=0=lnmwet,ri=0=r0,vi=0=v0

zi=N≥lnmdry,ri=N=rf,vi=N=vf

(95)

其中:约束式(95)为信赖域约束,是二阶锥约束,确保凸化的精确性,是算法鲁棒性的保证[18]。

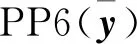
4 序列凸优化方法

序列凸优化将通过将原始非凸问题转化为一系列凸优化子问题进行迭代求解。每次需求解的凸优化子问题以上次迭代结果为基准,第1次迭代需要预先输入一个基准。

4.1 求解步骤

序列凸优化方法求解分为如下5个步骤：

步骤1初始化设计变量y0,及迭代次数n=0；

步骤2在yn处对非凸约束进行凸化,得到子问题PP6(yn)；

步骤3求解子问题,得到解记为yn+1；

步骤4检查是否满足收敛准则,若是,则算法结束,输出解yn+1,若否,则继续下一步；

步骤5n=n+1,返回步骤2。

s.t.

Ay-b≥κ0

Cy-d=0

(96)

(97)

4.2 结果可行性分析

首先验证算法收敛结果是否满足P6问题的所有约束,即解是否可行。给出如下定理。

定理3若算法得到的解数列{yn}收敛于解y*,则y*为P6*可行解。

证明：解数列{yn}收敛于y*,因此

y*=PP*(y*)

将y*代入PP*(y*)约束得：

(98)

即y*为满足P6*约束,因此y*为P6*可行解。□

4.3 结果最优性分析

定理4若PP*(yn)严格可行,解数列{yn}收敛于解y*,则y*为P6*的KKT(Karush-Kuhn-Tucker)解。

证明：P6*的拉格朗日函数为

(99)

式中：λ0、λi、υ0、υj为拉格朗日乘子。需要证明y*满足P6*的KKT条件[19],即原始约束式(100)、对偶约束式(101)、互补松弛式(102)以及拉格朗日函数导数为零等式(式(103))。

Ay-b≥κ0,Cy=d,gi(y)≤0,hj(y)=0

(100)

(101)

(102)

(103)

由定理3可知,y*满足原始约束式(100)。

PP*(yn)的拉格朗日函数为

(104)

PP*(yn)的对偶问题为

(105)

展开表示为如下形式：

(106)

由于y*为PP*(yn)最优解,因此y*满足对偶约束式(101)及拉格朗日函数导数为零等式(式(103))。

由于y*满足PP*(yn)约束,因此以下表达式成立：

(107)

由于PP*(yn)严格可行,y*满足PP*(yn)问题的SLATER条件,因此对偶间隙为0,即原问题最优值P*与对偶问题最优值D*的差为0,将式(107) 与式(103)代入得：

(108)

则有

(109)

由于

(110)

根据对偶锥定义[19]得：

(111)

因此有

(112)

由于对偶间隙为0且拉格朗日函数导数为0,因此以下表达式成立：

(113)

将yn=y*代入得：

(114)

又因为

(115)

所以

λigi(y*)=0

(116)

结合式(112),y*满足互补松弛条件式(102)。

综上,y*为P6*的KKT解。但实际求解中,由于精度限制,算法收敛结果接近P6*的KKT解。□

5 仿真验证

面向扰动环境下火星动力下降段自主轨迹规划问题,开展数值仿真研究,针对具体任务,进行仿真分析。硬件环境为Intel Core i7-6700 3.4 GHz PC,采用Yalmip进行问题描述与转化,采用Mosek求解器[20-21]求解,编程环境为MATLAB 2019b。

5.1 任务参数与算法参数

任务参数如表1所示。火星重力加速度g=[0,0,-3.114]TN/kg,初始位置r0=[0,2 000,1 500]Tm,初始速度v0=[0,50,-75]Tm/s,终端位置rf=[0,0,10]Tm,终端速度vf=[0,0,0]Tm/s。

表1 任务参数

设置控制时间间隔为0.01 s,重规划触发条件选择周期性触发,触发时间间隔为5 s,每次规划离散区间个数N=50,求解结果采用三次样条插值进行进一步离散。随机扰动上界设置为η=0.05(根据文献[22]中火星大气参数,当着陆器阻力系数为0.9,横截面积为2 m2时,以80 m/s的速度下降空气阻力所产生的加速度不超过0.049 8 m/s2),控制器参数选取为kp=0.2,

kd=2.1,根据引理1可以计算出rtube=0.25 m,vtube=0.026 3 m/s。

预规划问题P4初始终端时间基准设置为以火星重力加速度完成下降任务的时间的2倍,初始轨迹基准选择为连接始末位置的连线轨迹,初始速度基准为始末速度的连线速度,初始控制量基准在每个时刻设置为0。重规划问题初始时刻为根据上次规划结果构造的可行解。

5.2 自主规划结果

着陆器从预先位置触发,经过1次预规划,11次重规划后,抵达终点。预规划经过5次SCP迭代收敛,求解耗时0.935 6 s；11次重规划平均耗时0.565 8 s,最高耗时0.940 8 s。规划结果如图1 所示,不同颜色表示不同时刻的规划结果,符号“+”表示重规划触发时刻的位置,锥形区域为滑降约束。通过局部放大可以看出,由于下降过程中存在扰动,每次重规划结果的轨迹都会发生改变,但所有规划结果均可抵达目标位置。位置分量(rX、rY、rZ)、速度分量(vX、vY、vZ)、推力分量(TcX、TcY、TcZ)随时间的变化如图2所示,最终实际轨迹与多次重规划结果几乎完全相同。速度大小v变化与推力大小Tc变化如图3所示,可以看出推力大小满足约束。

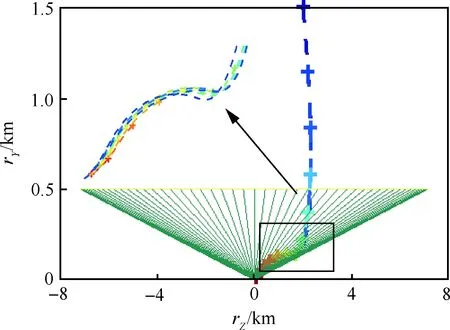
图1 下降规划结果

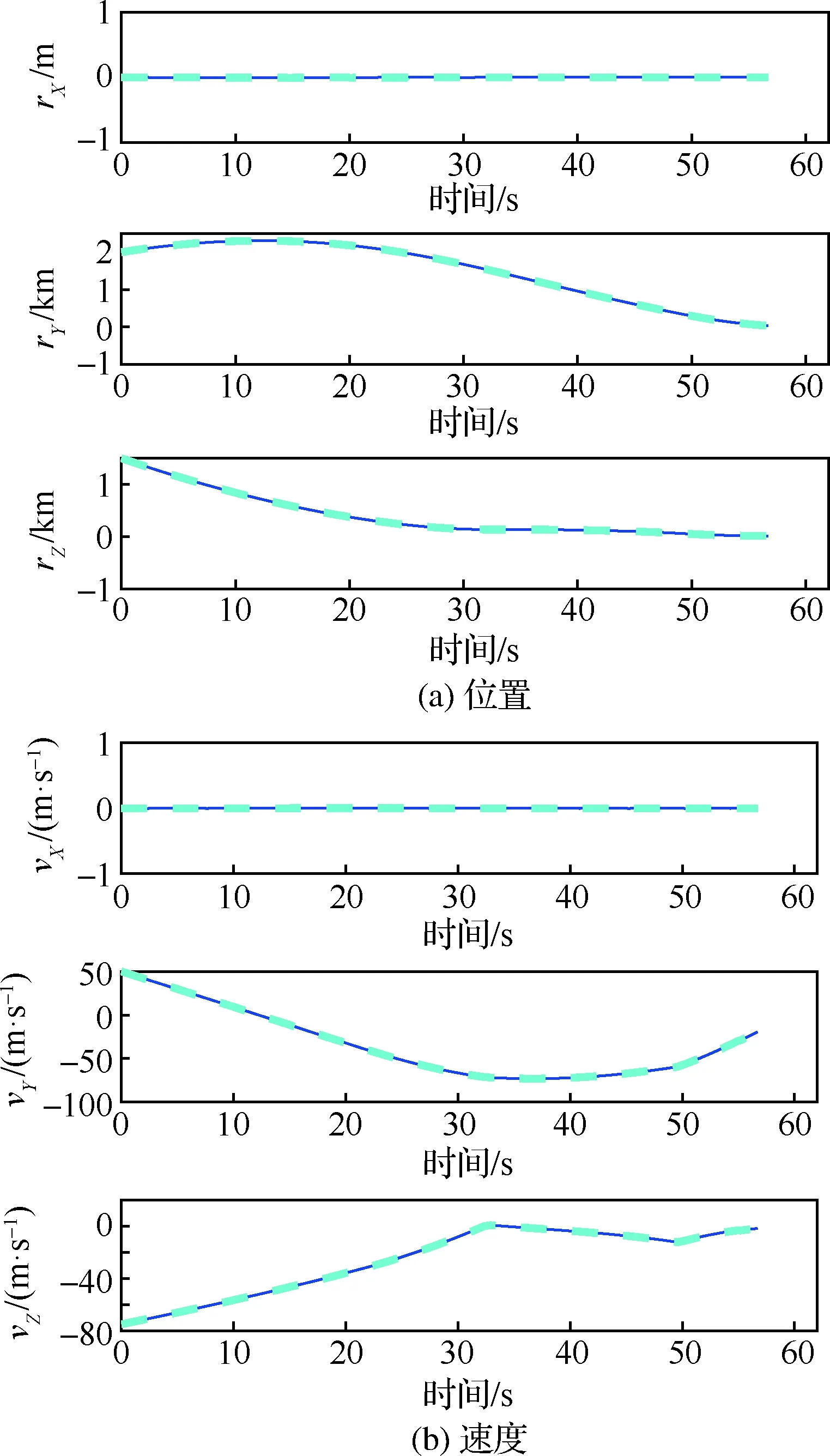
图2 状态及控制量变化(重规划与实际对比)

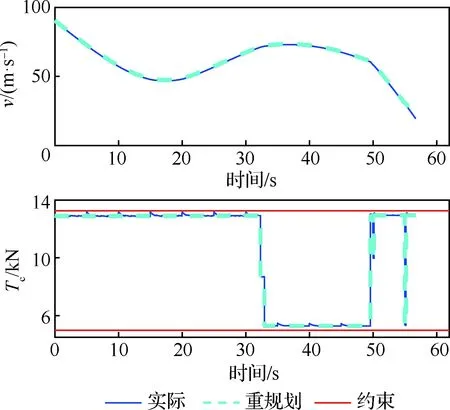
图3 速度大小与推力大小(重规划与实际对比)

实际位置与上次规划最优位置误差随时间的变化如图4(a)所示,速度误差随时间变化如图4(b) 所示。可以看出位置误差稳定在上述计算的rtube=0.25 m以内,仅在重规划初始时候略有超出,这是受重规划问题最优解离散精度的影响。同理,速度误差稳定在vtube=0.026 3 m/s以内,符合引理1结论。

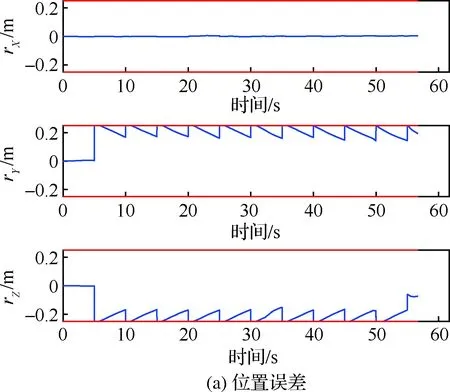
图4 状态误差变化

由于重规划问题与当前着陆器状态相关,因此重规划触发后,一般会引起误差突变,在下次重规划触发前,依靠线性反馈控制使误差逐渐收敛至有界,直至下一次重规划问题触发。

自主规划的最优值与最优终端时间情况如图5 所示。最优值呈现线性下降趋势,这是由于重规划中的代价函数没有考虑已经完成的轨迹代价。最后终端时间大体相同,但相比于预规划,略有减少,这是因为在重规划中修正了前次规划中次优的部分轨迹。

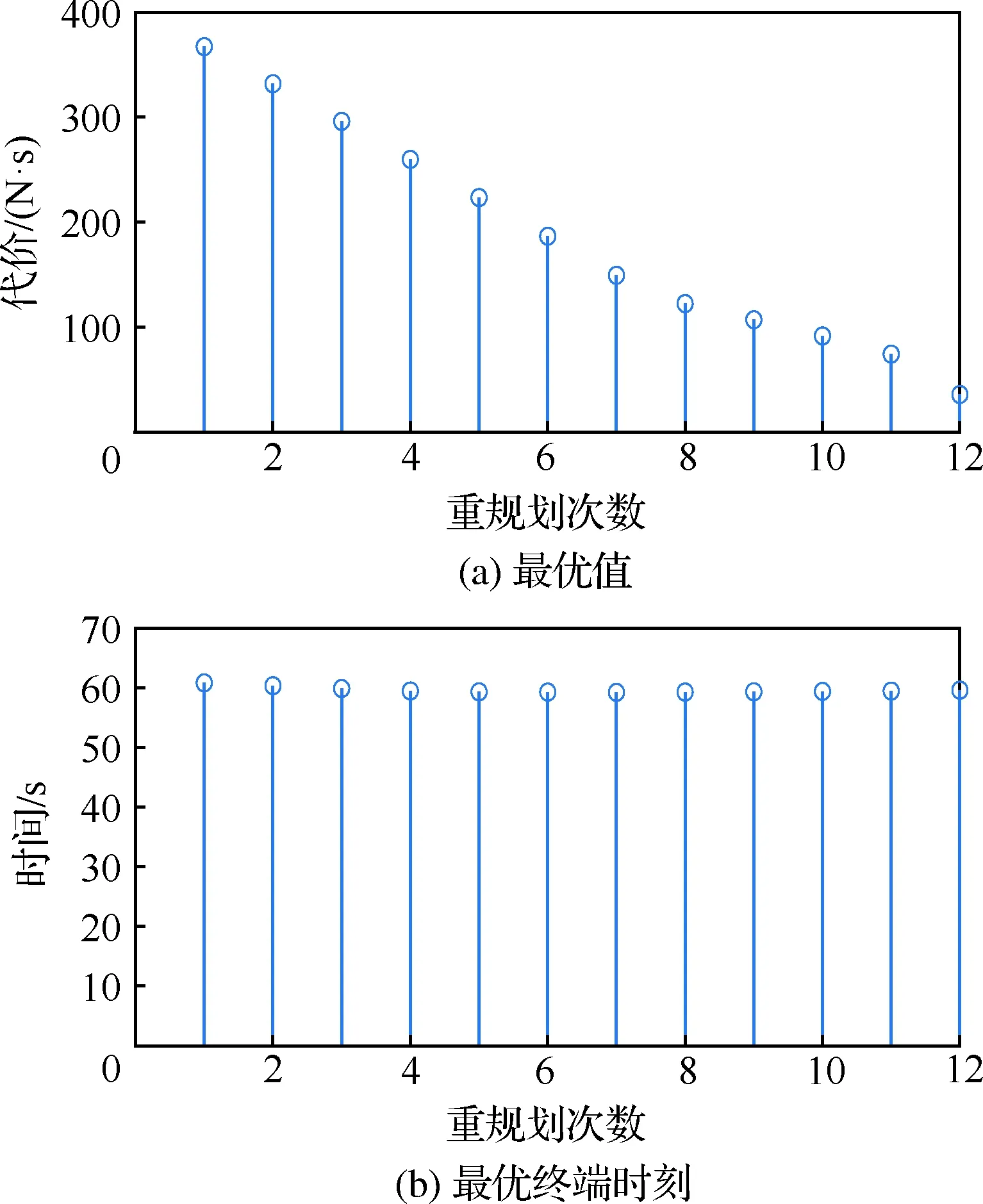
图5 自主规划的最优值与最优终端时间

5.3 规划结果对比

为进一步对比有无重规划的差异,在相同设置下进行了仅有预规划与反馈控制的仿真。仅有预规划时,下降时间为60.83 s,消耗燃料质量为292.035 5 kg；有重规划时,下降时间缩短至56.7 s,消耗燃料质量为272.607 0 kg。

实际上,在扰动作用下,预规划出的轨迹可能在出发不久就不是最优轨迹了,通过不断地重规划可以克服扰动影响并在一定程度上提高实际下降结果的最优性,减少下降时间。

将提出方法与文献[15]方法(PFGMPG)进行对比。重规划触发间隔为5 s,控制间隔为0.01 s,状态惩罚项系数设置为1。进行2组PFGMPG仿真,PFGMPG 1组中含有反馈控制律；PFGMPG 2组中不含反馈控制律,由规划结果直接控制。对比如图6所示。

从图6(a)中看出,含有反馈控制律的PFGMPG 1组在实际下降时推力违反了约束,这是

由于规划时忽略了控制环节的耦合作用,没有给内环控制器预留足够的抗扰控制量。从图6(b)中可以看出,在2次规划间隔内,提出方法位置误差在反馈控制律的作用下呈现逐渐减少趋势,而不加反馈控制律的PFGMPG 2组由于没有反馈,位置误差随着扰动影响逐渐增加；从图6(c)中可以看出不加反馈控制律的PFGMPG 2组的速度误差在2次规划间隔中可能超出约束,这是2次规划间隔中开环控制的直接结果。

6 结 论

针对扰动环境下火星着陆动力下降段自主轨迹规划问题,本文考虑终端时刻自由情况,建立预规划问题与重规划问题模型,使用SCP方法实现轨迹规划。给出了预规划问题可行的必要性条件,为控制器参数的选取提供参考。得到以下结论：

1) 在连续时间系统下,当预规划问题可行时,重规划问题可行,且可以构造出重规划问题可行解。

2) 误差线性反馈控制律参数在满足一定条件时可将实际轨迹约束在最优轨迹附近。

3) 在本文提出的重规划框架下,每次规划的最优值呈线性下降趋势,实际下降轨迹的时间略长于预规划出的下降时间结果。

4) 仿真结果表明,实际下降轨迹既可以保证在2次规划间隔内误差有界,又可保证推力满足推力大小约束。