一种改进的直方图概率多假设多目标跟踪方法

张奕群,尹立凡,王硕,孙承钢

北京电子工程总体研究所,北京 100854

未来强对抗的战场环境对目标跟踪系统的多目标处理能力提出了更高的要求。而传统的检测前跟踪(Track Before Detect, TBD)方法[1-3]在多目标情况下会遇到“维数灾难”问题[4]。为此人们致力于发展高效的多目标处理方法,直方图概率多假设跟踪[5](Histogram Probabilistic Multi-Hypothesis Tracking, H-PMHT)就是其中一种。该方法由Streit提出,其计算量与目标数呈线性增长,因而在多目标情况下仍可以保持较高的计算效率[5]。

H-PMHT方法有这一优势的关键在其多项式分布(Multinomial Distribution, MD)量测模型[6-7]。Streit等使用期望极大化(Expectation Maximization,EM)方法[8]在经验贝叶斯意义下对该模型未知分布参数进行了估计,其结果是包括目标状态和强度参数在内的未知参数寻优过程可以被解耦为多个易于计算的子寻优过程,由此为H-PMHT方法计算量与目标数呈线性关系奠定了基础。

在H-PMHT方法基础上,Davey等以多维泊松分布(Poisson Distribution, PD)替换了多项式分布[9],从而得到了不同目标强度参数互相解耦的改进的量测模型。因而,以此得到的泊松H-PMHT(Poisson H-PMHT,P-HPMHT)方法可以在估计中利用强度参数先验信息并同时保持计算量与目标数间的线性关系。因为P-HPMHT方法在目标数目较多时仍可以有效的利用先验信息,其表现比H-PMHT方法更为稳定[10]。

H-PMHT方法的一个主要问题是在低信噪比条件下跟踪能力较差。Davey等在文献[1,11]中通过仿真对包括H-PMHT方法在内的几种TBD方法的跟踪检测能力进行了比对研究,研究表明H-PMHT方法的低信噪比跟踪检测能力较弱。究其原因,H-PMHT方法的量测方程中并未考虑传感器噪声[12]。因此,其跟踪检测能力在低信噪比条件下会明显降低。自2000年提出至今H-PMHT方法对这一问题仍未能解决。其难点在于如果在多项式分布量测模型中引入噪声模型,则量测量的分布难以处理,进而无法得到有效的跟踪方法。P-HPMHT方法也存在相同的问题。目前,这一问题仍然没有解决[12-13]。

在H-PMHT方法中使用MD模型为量测模型,其中隐含着一个前提假设,即存在一个量化单位使得传感器数据量化结果满足多项式分布。然而,在实际中该量化单位无法确切得到,或并不存在。因此,若量化单位取值偏差较大,将导致估计结果误差增加。为解决这一问题,Streit提出了一种“修正先验信息”(Modified Prior)方法[5],以补偿量化单位取值偏差对估计精度的影响。随后,Davey等也使用了类似的方法解决了P-HPMHT方法存在的相同问题[9]。然而,这种解决方法是一种工程中的变通方法,其缺乏理论依据[14]。Willett等在文献[15]中以目标的状态估值为条件对量化单位进行了寻优。但该方法目标的状态估计受到量化单位估值误差影响,导致其估计仍存在偏差。

本文提出了一种带传感器噪声模型的H-PMHT方法：通过选择恰当的量测模型丢失数据,实现了引入噪声模型条件下寻优过程的解耦。又通过提出一种类泊松概率质量函数多重卷积简化计算方法,实现了寻优过程的高效计算。最终,在引入噪声模型条件下实现了计算量随着目标数线性增长。且同时,这一方法还给出了一种理论化的量化单位寻优办法。

全文内容安排如下：第1节,给出了使用到的符号与定义,并引出了要解决的问题；第2节,提出了带噪声模型的H-PMHT方法；第3节,在单目标低信噪比、双目标交叉及平行运动的场景下做了仿真实验,对比了H-PMHT方法、P-HPMHT方法、本文提出的跟踪方法和经典的联合概率数据关联(Joint Probabilistic Data Association,JPDA)方法[16]；第4节,总结了主要结论,并指出了后续还需要关注的问题。

1 符号、定义与问题的引出

(1)

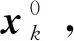
(2)

(3)

为第k时刻强度参数的集合。

假设传感器空间B分为I个不相交的传感器分辨单元。记其中第i号分辨单元子空间为Bi⊂B,第k时刻其上分布的来自目标及杂波的能量一般表示为[1]

(4)

式中：i=1,2,…,I。

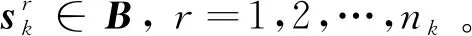
(5)

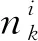
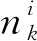
(6)

与之对应的传感器输出为

(7)

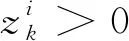
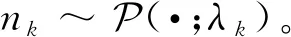
(8)

H-PMHT方法和P-HPMHT方法的量测模型方程均为

(9)

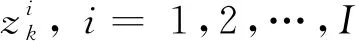
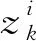
2 带传感器噪声模型的H-PMHT方法

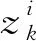
(10)

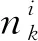
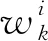
(11)

(12)

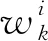
(13)

令量化输出

(14)

(15)

式中：*为卷积运算,f(x)|z为函数f在z处取值。

(16)

将式(16)代入式(11),即可以得到传感器输出Zk的改进概率模型p(Zk;Xk,Λk,η)。

令参数集

Θk={Xk,Λk,η}

(17)

以下,要解决的主要问题是通过求解式

(18)

来得到Θk的极大后验估计。式中：p(Zk|Θk)为式(11)；pΘ(Θk)为Θk的先验分布。

2.1 EM方法

在H-PMHT方法、P-HPMHT方法等一类估计问题中,都通过使用EM方法[7-8]对其模型参数进行寻优。本文也采用相同的方法求解式(18)。

根据EM方法,式(18)的优化问题可以变换为式(19)定义的一系列寻优问题

(19)

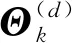
(20)

式中：Ok为丢失数据(Missing Data)的集合。

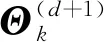
式(20)中,丢失数据Ok的选择非常重要。只有选择恰当的丢失数据Ok,才可以使得Q能够解耦,从而易于计算。

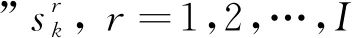
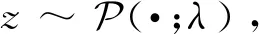
由式(8)可知,计数值

(21)

其中,

(22)

式中：

(23)

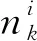
(24)

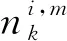
记来自第m号密度分量并落在Bi上的“样本点”为

而后,分别定义集合

(25)

i=1,2,…,I}

(26)

这里丢失数据为

(27)

2.2 期望步骤

期望步骤的目标是计算辅助函数Q,其定义见式(20)。根据贝叶斯公式,得到该函数表达式中的对数项为

lgp(Ζk,Ok,Θk)=lgp(Ζk,Ok|Θk)+lgp(Θk)

(28)

式中：等号右侧第1项为Ζk和Ok的对数联合条件概率密度函数；第2项为Θk的对数先验分布。

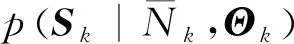
(29)

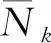
(30)

利用以上结果及概率乘法公式,即可以得到丢失数据Ok的条件概率密度函数为

(31)

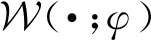
(32)

将式(32)与式(31)相乘,利用条件概率乘法公式得到Ζk和Ok的联合条件概率密度函数为

(33)

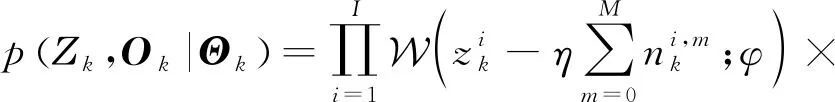
(34)

对式(34)等号两边求对数,可以得到

(35)

式中：C为与Θk无关的量。

假设各目标状态间相互独立,Xk的先验密度函数为

(36)

式中：pX为目标状态的先验密度函数。

假设Λk的先验密度函数为

(37)

式中：pΛ为强度参数的先验密度函数。

又假设Xk和Λk相互独立,得到Θk的对数先验密度函数为

(38)

将式(35)和式(38)一并代入式(28),对其等号两侧求条件期望E[·|·],而后利用约束条件

(39)

进行整理,辅助函数Q为

(40)

在式(40)中,等号右侧第1项仅与η相,第2～4项仅与Λk相关,第5～6项仅与Xk相关。易见辅助函数Q的极值求解问题被拆分成多个独立的极值求解问题。

根据贝叶斯公式知,丢失数据Ok的条件密度函数为

(41)

其中分母和分子项依次见式(11)及式(34)。利用该结果将式(40)做化简,其等号右侧第3行中的条件期望可以整理为式(33)。

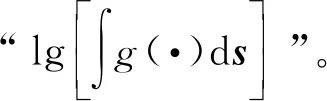
2.3 极大化步骤

接下来,计算式(40)的极值。首先,将式(40)整理为

(42)

式中：各分量为子辅助函数,其定义分别为

(43)

(44)

(45)

假设目标状态的演化规律可以用一阶马尔科夫模型来描述,则由C-K方程可得

(46)

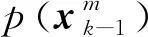
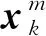
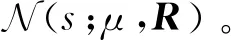
(47)

(48)

式中：

(49)

(50)

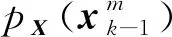
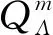
(51)

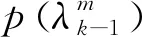
(52)

因而,借鉴Granström等提出的一种泊松强度参数滤波方法[19]对式(52)寻优。假设

(53)

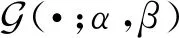
(54)

式中：ξ为遗忘因子；Δ为不同采样时刻时间间隔。可以得到其更新方程为

(55)

(56)

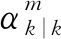
2.3.2 求Qη的极值

假设传感器噪声为高斯噪声,即

(57)

式中：μ为噪声均值;σ2为噪声方差。

对Qη表达式(45)中的对数项进行展开,得

(58)

计算式(58)展开结果中各项条件期望E[·|·],得到Qη展开为

(59)

对式(59)求导并令其为0,进而得到η的估计值为

(60)

式(60)计算过程中涉及到的2个期望值的计算问题,将在2.4节中讨论。另外,以上为高斯假设下得到的估计方法,对于非高斯情况,Qη的极大化问题有待进一步研究。

引理定义函数族

(61)

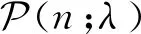
(62)

式中：cq为系数,其具体值由λa、λb、qa及qb计算得到。

(63)

因为2个函数卷积的特征函数等于其各自特征函数的乘积,所以证明等式(62)成立等价于证明存在系数cq使得

(64)

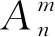
(65)

(66)

不失一般性,假设0≤qa≤qb。利用以上特征函数表达式,通过合并同类项可得

Pqa(τ;λa)×Pqb(τ;λb)=e(λa+λb)(ejτ-1)·

(67)

式中：系数

(68)

由式(65)～式(68)结果知,式(64)成立,又等价于存在系数cq使得

(69)

当m>n时,S(n,m)=0,将式(66)代入式(69) 等号左侧,即可得到

(70)

对照式(70)与式(67)知,若cq存在,即向量

(71)

存在,矩阵方程

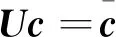
(72)

可解,式中：向量

(73)

矩阵U为(qa+qb+1)×(qa+qb+1)的上三角阵,且其中第i行、第j列元素为

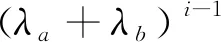
(74)

因为,S(j-1,i-1)=1、λa和λb都大于0,在矩阵U对角线上各项非0,所以其行列式非0。因此,存在逆矩阵U-1。也因此,向量c存在且

(75)

因此,引理证明成立。

(76)

式(76)中第2个等号成立是因为式(13)成立。

(77)

式中：系数c1为

(78)

它由式(75)计算得到。

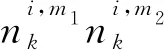
当m1=m2=m时,其条件期望为

(79)

当m1≠m2时,其条件期望值为

(80)

则使用前述引理可将上述2种情况都化简为

(81)

式中：当m1=m2=m时,系数cq依次为

(82)

当m1≠m2时,为

(83)

进一步,利用以上结果还易得

(84)

因而,还可以得到更简化的计算式

(85)

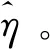
总结以上过程,对Θk进行估计,其步骤如下：

步骤1初始设置

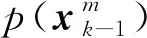
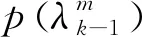
设定量化单位初始值η(0)为上一时刻估计值。

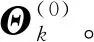
设定迭代次数计数值d=0。

步骤2迭代更新

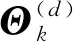
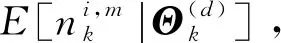
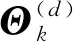
更新迭代次数计数值d=d+1。

步骤3回到步骤2,直到估计结果收敛。

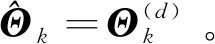
3 仿真验证

在仿真中,假设传感器空间B为xOy二维坐标平面上的正方形区域,其右上顶点为坐标原点O且两直角边分别在x轴及y轴上。设定传感器共包含20×20个分辨单元。以(i,j)表示沿x轴向第i行,沿y轴向第j列的分辨单元,设定其空间为正方形区域[(i-1)Δl,(j-1)Δl]×[iΔl,jΔl],其中Δl为每个分辨单元的边长。设定Δl=0.5。

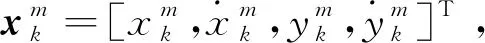
(86)

式中：F为状态转移矩阵

(87)

ωk-1为高斯过程噪声,其均值为0,协方差阵为

(88)

式中：qω表征噪声强度,设定qω=0.001。

假设第m号目标的能量分布为高斯密度函数

(89)

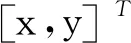
记式(84)在第(i,j)号分辨单元上的积分为

(90)

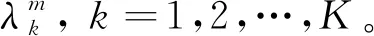
仿真中,模拟第(i,j)号分辨单元的输出为

(91)

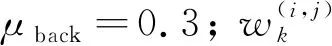
进而,定义目标的信噪比为

i,j=1,2,…,I

(92)

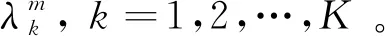
根据以上给出的参数,在目标信噪比为10 dB 和6 dB场合使用到的2帧传感器数据的示意图见图1。其中,目标位于左下角圆圈中心,目标强度扩散3×3个分辨单元。在10 dB时,目标还可能被分辨出来,但6 dB时,已经不能分辨出其位置。

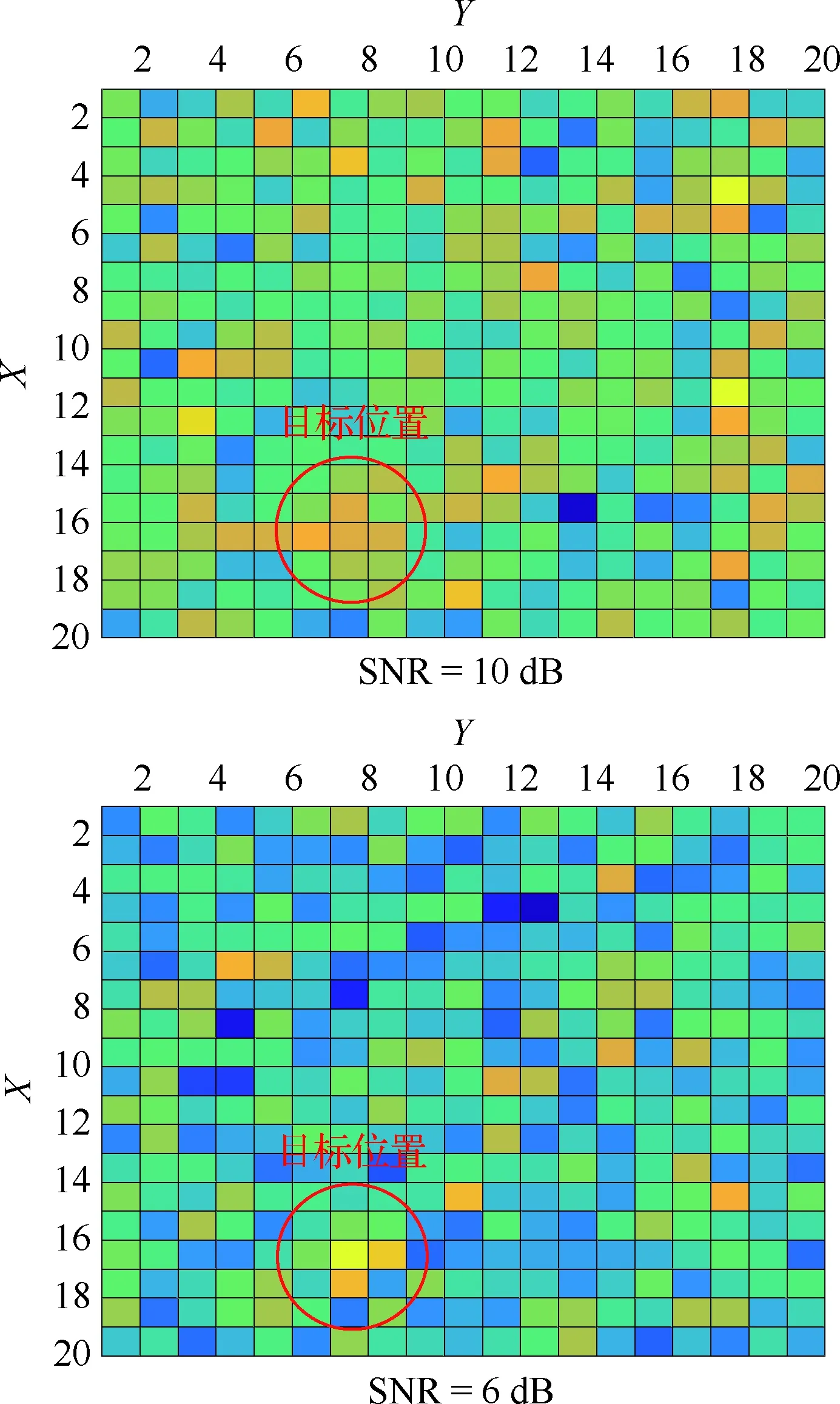
图1 仿真数据示意

3.1 仿真场景

场景1单个目标做匀速直线运动。目标的起始状态为x0=Δl[16.5,-1,5.5,1]T,即目标初始位置在分辨单元(17,6)的中心位置且其运动速度沿x轴及y轴分别为-1和1分辨单元/帧。目标的真实轨迹序列为X={xk:k=1,2,…,K},其中K设定为11帧。设定目标信噪比SNR分别为10、6和3 dB,根据式(91)模拟生成1 000组×11帧的传感器数据。再以无目标情况模拟生成1 000帧仅有噪声的传感器数据。

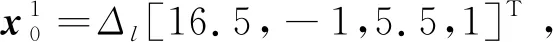
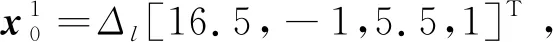
3.2 跟踪实现及性能评价

在场景1中,以H-PMHT方法、P-HPMHT方法及本文提出的H-PMHT/SN方法跟踪目标。其中,第k时刻本文方法的工作分为轨迹起始和轨迹维持2个部分。

1) 轨迹起始：设定检测概率为0.9,在给定的信噪比条件下确定检测门限。分割第k帧数据以得到该时刻的目标,并与前一帧目标关联构建新的轨迹。其条件为相应的目标间的距离小于1.5Δl。

利用M/N准则[6]管理轨迹,其中M为2,N为3,即连续3帧轨迹质量的测度大于门限,则维持这一轨迹,否则将其删除。其中,轨迹质量,即信噪比估计值按下式计算[6]

(93)

根据仿真结果,从跟踪检测能力和估计精度2个方面对跟踪方法进行评价。其中,以特征曲线(Receiver Operating Characteristic,ROC)评价跟踪检测能力；以位置估值的均方根误差(Root Mean Square Error,RMSE)评价各方法的估计精度。ROC定义为检测比率相对误跟踪比率的函数曲线。首先使用某一跟踪方法处理1 000帧仅有噪声的传感器数据,则检测到“目标”的一帧称为“误跟踪”帧。以“误跟踪”帧数比总的帧数为该跟踪方法的误跟踪比率。其中“误跟踪”帧的判据是：某一帧和与之相连的前2帧中估计得到的3帧轨迹,其中有任2帧的目标位置估值与目标真实位置间的距离误差大于2σsp。而后使用给定的跟踪方法处理不同给定信噪比条件下生成的1 000 组×11帧数据,其中正确检测到目标的总的帧数比总的帧数,即为检测比率。由此,得到的ROC曲线为图2。

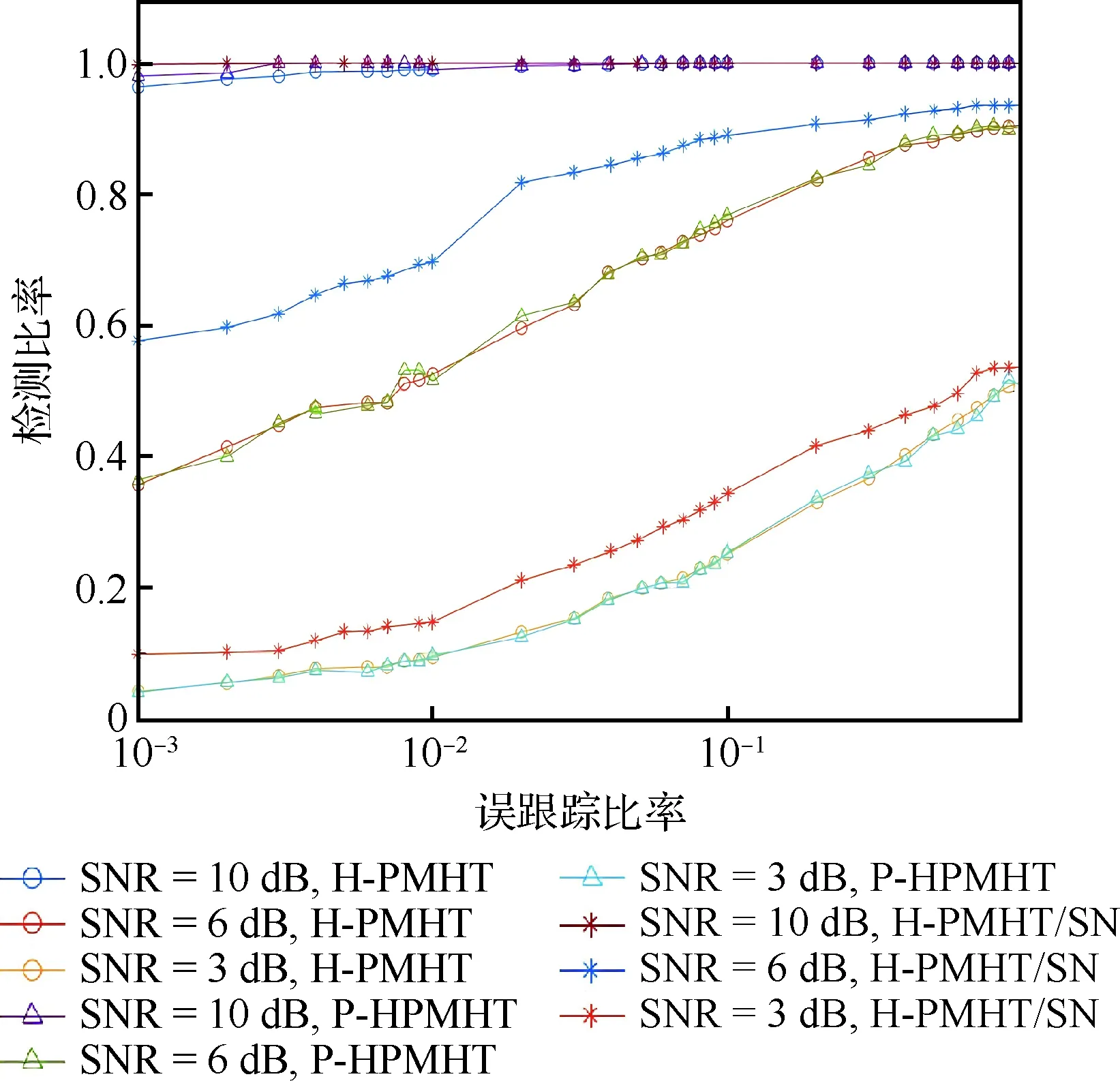
图2 ROC曲线

从结果看在低信噪比条件下,本文跟踪方法较H-PMHT方法和P-HPMHT方法表现更好,尤其是在信噪比为6 dB及3 dB时。以误跟踪比率为10-3时结果进行分析,在信噪比为6 dB时,本文方法检测比率提升了20%,信噪比为3 dB时,提升了10%。另外,各方法RMSE见图3。可以发现当跟踪上目标时,各方法的精度相近。

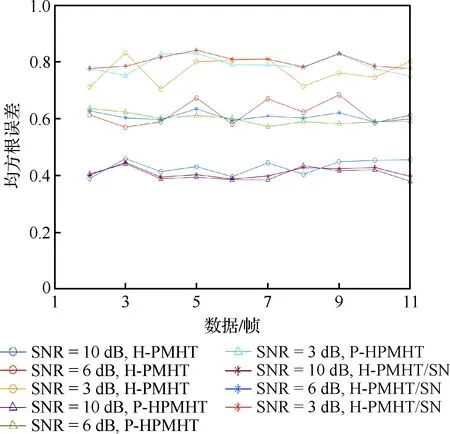
图3 RMSE图示

设置场景1的目的是对H-PMHT/SN方法的低信噪比跟踪能力进行评价。场景2则是检验

该方法在2个目标交叉运动时的跟踪能力。

以下采用轨迹丢失率(Track Loss Ratio,TLR)对跟踪结果进行评价。TLR定义为“误跟踪”的轨迹数比上总的蒙特卡洛仿真数。其中,“误跟踪”与仿真1中给出的定义相同,仿真数为1 000次。

在10 dB和6 dB信噪比条件下,比对跟踪方法的轨迹丢失率,见图4。当信噪比为10 dB时,H-PMHT、P-HPMHT和H-PMHT/SN这3种方法总体上保持了较低的轨迹丢失率,且并没有受到轨迹交叉的较大影响。但JPDA方法在轨迹交叉时,其轨迹丢失率明显升高。出现这一结果的原因是H-PMHT、P-HPMHT和H-PMHT/SN这3种方法是TBD算法,它们更充分地考虑了目标接近时的相互影响,也较少受到轨迹交叉影响。

当信噪比为6 dB时,H-PMHT和P-HPMHT方法的轨迹丢失率都出现了明显的上升。这是因为H-PMHT一类方法的收敛结果与迭代初值密切相关,而初值由前一时刻的估值所确定。因为噪声影响,6 dB时初值误差随时间积累加快,会导致这类方法轨迹丢失率增大。从结果看到,H-PMHT/SN方法跟踪效果也受初值误差累积的影响,但它利用了噪声信息,因而仍保持了较低的轨迹丢失率。该结果还可以由图4体现,H-PMHT和P-HPMHT方法的轨迹在末尾处偏差较大。另外,可以由图5发现JPDA方法在6 dB时的表现最差,其轨迹丢失率在轨迹交叉之后并未降低。这是因为在6 dB时该方法很难再纠正轨迹交叉时被“拉偏”的轨迹。

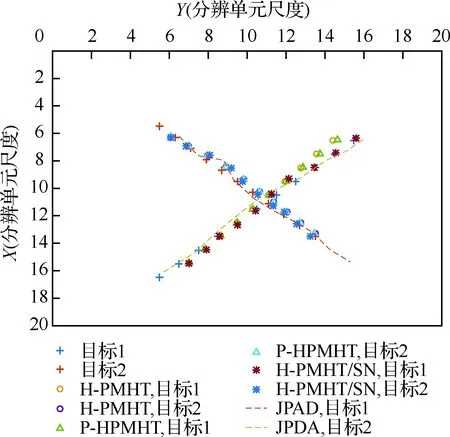
图4 场景2中的典型跟踪结果

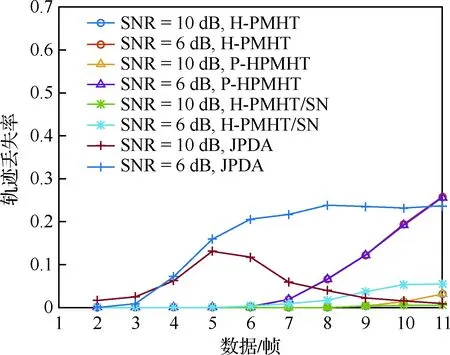
图5 场景2中的轨迹丢失率

场景3与2类似。所不同的是,2个目标的运动轨迹保持平行。在场景3中,一个典型跟踪结果见图6。图中,目标1和目标2从左下角向右上角运动,其间距离保持为2个分辨单元。同场景2一样,分别在信噪比10 dB和6 dB下,比对4种跟踪方法的轨迹丢失率,见图7。当信噪比为10 dB时,前3种方法都保持了较低的轨迹丢失率。但JPDA方法却表现较差。究其原因,目标在场景3中始终保持较小的间距,因而通过JPDA方法跟踪目标,轨迹有更大的概率被另一目标点迹“拉走”。这一现象也可以在图6中体现,其中不同目标轨迹发生交叉。当信噪比为6 dB 时,噪声对跟踪结果的影响更为突出。H-PMHT和P-HPMHT这2种方法的轨迹丢失率都出现了十分明显的上升,H-PMHT/SN方法却仍有能力保持较低的轨迹丢失率。这时该方法利用噪声统计特性的能力得到了体现。同样的,还可以发现这种程度的信噪比条件下JPDA方法的表现最差。

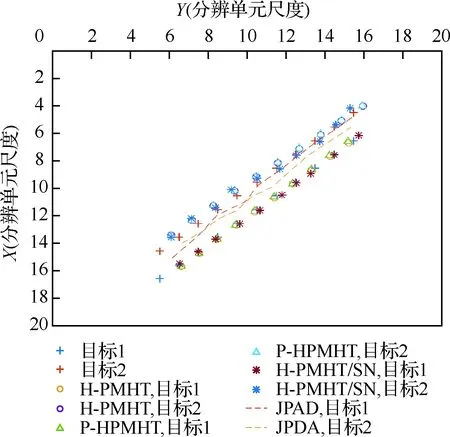
图6 场景3中的典型跟踪结果

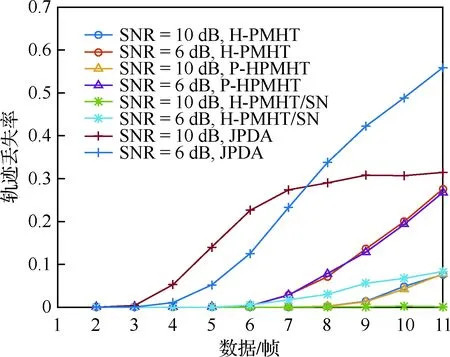
图7 场景3中的轨迹丢失率

4 结 论

1) 本文提出了一种带噪声模型的H-PMHT方法,即H-PMHT/SN方法。该方法较传统的H-PMHT方法和P-HPMHT方法在低信噪比条件下有着更强跟踪检测能力。同时,在多目标情况下,其计算量与目标数仍能保持线性关系。这为其实际应用提供了广阔空间。

2) 该方法对目标状态、强度参数及量化单位同时进行了估计,其中量化单位的估计准则为极大似然。在理论层面,它解决了量化单位真实值未知而导致的估计结果偏差问题。同时,还为工程中避免再使用“修正先验信息”这一变通方法提供了一种可行的解决办法。

3) 量化单位的估计值可能被用作构建惩罚函数来辨识目标总数M[14,15]。另外,本文并没有给出Θk估计误差的协方差阵,这将影响其滤波效果。这些问题有待进一步研究。