考虑连接非线性的大型桁架天线分散协调控制

刘付成,朱东方

1. 上海航天技术研究院,上海 201109

2. 上海航天控制技术研究所,上海 201109

3. 上海市空间智能控制技术重点实验室,上海 201109

随着航天技术的不断发展和高时空分辨率遥感任务的迫切需求,柔性化和大型化逐渐成为新一代航天器的发展趋势。对于尺度上远超传统航天器的新一代大型柔性航天器,由于受运载能力制约,高收纳比可展开桁架结构逐渐成为大型柔性载荷的主要承载形式。虽然可展开桁架式载荷满足了遥感任务对尺度和重量的需求,但由于多次展开方式导致结构中含有大量运动副铰链,而加工、装配、磨损等客观因素使得运动副铰链即使锁定后依然存在一定的间隙。而间隙引发的铰链部件间的碰撞/摩擦等非光滑特性和低刚度柔性特性共同作用将对航天器的动力学特性造成较大的影响[1-3],从而给航天器的高精度控制带来困难。另外航天器长期在轨运行期间,受到空间环境多种不确定因素的影响,易激发所装载大型柔性结构的挠性振动；同时由于大型柔性结构自身阻尼较低,其挠性振动被激发后衰减非常缓慢,易造成结构疲劳损伤甚至影响航天器系统的整体稳定性。

目前国内外学者针对含间隙铰链的机构或结构展开了大量的研究,并取得了一系列成果。Salahshoor等[4]采用多尺度方法对含多间隙铰的机械系统进行了振动分析,详细讨论了主共振和内共振,研究结果表明摆角受间隙影响不大,滑摆振动固有频率与系统垂直运动固有频率相差甚远。Flores和Lankarani[5]研究了含多间隙铰链的多体系统动力学响应规律。荀剑和阎绍泽[6]基于小波变换研究了含间隙太阳能帆板,系统分析了间隙对动力学性能的影响,实现了对航天器可展结构动力学性能在时频域内的“精细”描述。孙杰等[7]针对含间隙铰接的柔性航天器开展了研究,首先利用哈密顿原理和模态离散方法,建立了含间隙铰接柔性航天器的非线性动力学模型,并研究了铰链间隙对姿态运动和结构振动的影响规律,最后采用压电纤维复合材料MFC(Macro Fiber Composite)驱动器研究了主动振动控制方法。

为了降低模型复杂度,传统的铰接组合结构动力学研究通常忽略了铰链质量和刚度,即使在考虑铰链质量和刚度影响[7]的研究中,也将铰链刚度假设为常值,而未考虑铰链间隙导致的非光滑接触碰撞对铰链刚度造成的影响。然而含间隙的铰接结构是一个强非线性系统,外激励、铰链间隙和铰链振动幅值均能改变铰链的动刚度系数[8]。袭安等[8]针对大型环形桁架天线中的间隙铰,建立了铰链动刚度的模型,分析了外激励、铰链间隙及铰链振动幅值对动刚度系数的影响,研究结果表明间隙对动刚度系数的影响较为显著,最后通过实验验证了理论模型的正确性。因此,在含间隙的铰接组合结构尤其是含众多间隙的大型桁架组合结构中,若采用常值的铰链刚度建立动力学模型,将造成较大模型误差。

在实现精确描述大型空间结构动力学特性的基础上,开展其主动振动控制问题也一直是航天领域研究的重点内容。Hu等[9]和Kar等[10]采用H∞鲁棒控制方法,实现了柔性板的主动振动控制。Luo等[11]采用压电作动器,实现了大型桁架结构的比例-微分(PD)振动控制。Hu等[12]设计了自适应控制器,实现了大型空间悬臂柔性结构主动振动控制。许睿和李东旭[13]采用周期变论域,设计了变论域自适应模糊控制器,有效抑制了柔性太阳能帆板的振动。上述研究成果主要是采用集中式控制策略,但随着大型柔性结构的出现,其尺度可达百米量级,控制所需的传感器和作动器数目大幅增加,造成控制系统庞大且复杂[14]。为了提高集中控制器的求解效率,一般采用独立模态控制方法来减小控制器求解维数；而对于模态相对密集的大型空间结构,这种处理方式容易造成观测溢出或系统失稳。此外,集中式控制策略是采用单一控制器的形式,当唯一的控制器发生故障时无法保证系统的容错性能。

针对上述问题,学者们研究了应用智能材料或智能元件的分散式主动振动抑制方法,以解决大型空间结构在扰动情况下的稳定控制问题。目前学者们已研究了多种控制方法,可有效地抑制大型柔性结构的振动,例如混合正反馈(HPF)控制方法[15]、正位置反馈(PPF)方法[16]、基于最小能量的控制方法[17]、基于Lyapunov函数的非线性振动控制方法[18]、极点-配置-积分谐振控制方法等[19]。Li等[20-21]针对大型柔性结构分散化振动控制问题,开展了系统性研究,进行了卫星太阳能帆板和大型智能桁架结构分散化振动控制的理论研究与实验验证。“分散式”的控制方法可在实现整体结构振动控制的前提下,有效降低控制器的设计复杂度,继而提高计算效率。王恩美等[22]针对大型太阳能帆板主动振动控制器设计复杂、难以重复扩展且容错性能低等问题,提出了一种分布式控制方法,基于控制子模块的动力学模型直接设计控制器,并通过子模块的独立控制以及彼此间信息交互设计了整体结构振动控制器。

但随着柔性结构尺度变大,所需执行元件越来越多,分散化所构成的分布参数化控制系统越来越庞大,进一步需考虑分散化多子系统的协调问题,以提高控制系统容错性和鲁棒性等性能。目前,针对多无人系统(车、飞机、机器人、微小卫星)的姿态/位置协同控制问题[23-26],基于图论一致性理论的研究有了较成熟及全面的理论分析,而针对大型柔性结构设计分散式协同控制策略的研究还非常少。其中,Omidi和Mahmoodi[27-28]将一致性理论分别应用于简单的均质固支梁和悬臂梁的振动抑制问题,与集中式控制方法相比,得到了较好的控制效果。然而,尚未见一致性理论应用于考虑连接非线性的大型柔性结构高精度形面保持控制问题的研究。

因此,本文针对含非线性连接的大型桁架式天线,根据其结构特征,采用模态综合方法将满足线性弹性理论的部分作为线性子结构,并将铰链作为非线性连接子结构进行建模,进而建立低维的非线性动力学模型。在此模型基础上,将其转换为分散参数化模型,考虑状态变量的不完全可测因素,设计适用于一致性理论的最优观测器,并基于图论的思想进行系统的通信拓扑结构分析,将分布式最优观测器估计得到的模态坐标及其速度信息作为控制子单元的状态反馈信息,然后基于主从式结构设计一致性形面保持控制器,由于通过一致性的约束条件使相邻控制子单元相互合作,保证了各控制子单元间的不一致性收敛至零,从而在短时间内实现了各独立控制子单元间的同步。另外,本文所设计的一致性分散化控制方法具有很强的鲁棒性,其原理是通过参考邻近控制子单元的性能来补偿当前控制子单元的故障,相比于传统的集中式控制方法,该方法对作动执行机构的失效具有一定的容错性。

1 含非线性连接大型桁架式天线的动力学建模

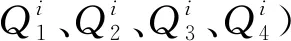
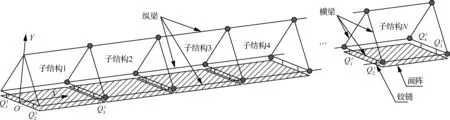
图1 大型桁架式天线结构示意图

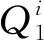
对于此类含非线性连接的大型桁架式天线,为了建立反映其非线性特性的低阶模型,根据结构特征,采用连接子结构的模态综合法[29],将支撑桁架和面阵等满足线性弹性理论的部分作为线性子结构进行建模,将铰链作为非线性连接子结构,采用广义弹簧单元进行建模。

建立第i个铰链非线性连接子结构的刚度矩阵为

(1)

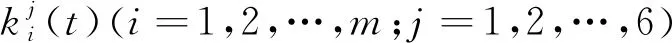
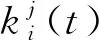
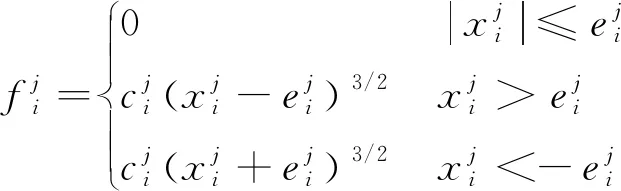
(2)

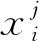
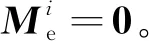
建立桁架式天线中n个铰链非线性连接子结构线性部分(锁定自由度)构成的质量矩阵和刚度矩阵分别为

(3)

然后基于有限元方法分别获取支撑桁架和面阵的质量矩阵和刚度矩阵,结合式(3),建立桁架式天线动力学模型为

(4)

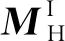
根据动力学方程(式(4)),采用固定界面模态综合方法,根据模态截断准则,忽略高阶剩余模态的影响,保留低阶主模态,进行模态降阶。建立支撑桁架和面阵模态坐标与物理坐标的关系为

(5)

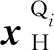
根据支撑桁架与面阵连接位移和力双协调条件,建立模态坐标变换矩阵为

(6)

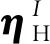
(7)

式中：T2、η分别为满足双协调条件的模态矩阵和模态坐标；Ω为模态刚度矩阵。式(7)不仅降低了动力学模型维数,同时也描述了系统非线性特性,可作为控制系统设计的理论模型。

2 控制器设计

2.1 模型转换

为了便于分散协同控制器设计,首先将桁架式天线振动方程(式(7))转换为分散参数化模型；根据振动测量信息解算出N个控制元件所在位置的N个形变位移信息,将每一组形变位移信息与控制元件构成一个控制单元,得到N个彼此连接、交互的控制单元；再根据动力学模型,将每一组形变位移信息变换为由n阶全局模态坐标描述。

建立桁架式天线对应于各控制单元的N组相似的分布式振动子系统状态方程：

(8)

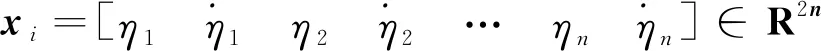
由于式(8)为线性时变系统,采用主从式协同控制策略,设计桁架式天线高精度形面保持控制器。

2.2 观测器设计

考虑到桁架式天线结构的被控状态量(全局模态坐标)不能通过测量敏感器直接测得,且形变速度信息通常也较难获得,因此构建最优观测器：

(9)

(10)

(11)

式中：Pi为Riccati方程的唯一正定解,有

(12)

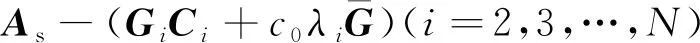
2.3 基于图论的大型桁架式天线形面保持一致性控制器

首先,基于图论思想进行系统的通信拓扑结构分析,确定连通路径,保证所有的跟随者直接连通或通过网络中的路径间接连接领导者。然后,根据形面高精度保持的控制目标,确定一个虚拟的领导者(即全局模态坐标及其速度为0),其他所有控制子单元跟踪其领导者,同时所有跟随者之间的误差收敛至0。通过分布式最优观测器估计得到的模态坐标及其速度信息作为控制子单元的状态变量,设计基于主从式的积分型一致性控制器结构为

(13)

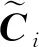
(14)

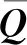
结合分布式振动方程、最优观测器和积分型控制器结构,增广的全局分布式协调系统为

(15)

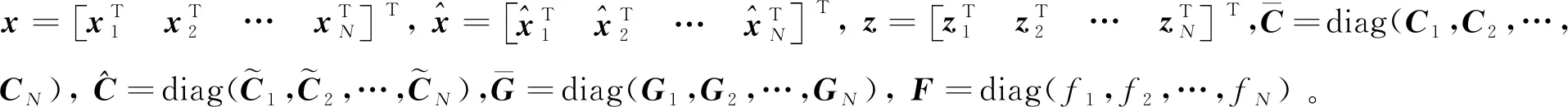
最后根据增广的误差动力学方程,采用预测控制方法,通过遗传算法进行优化,得到系统稳定的控制增益Φ和fi,在满足作动执行机构输入上限约束的基础上,实现形面保持控制系统的渐近稳定,并具有一定的鲁棒性。根据建立的一致性动力学模型,一致性约束条件令相邻控制子单元相互协调,使各子单元间的不一致收敛到0,在短时间内实现各独立子单元之间的同步,这种一致性控制方法为柔性结构的振动抑制带来了额外的鲁棒性,通过参考临近子单元的性能来补偿本单元的故障,相比于传统的集中式控制方法,基于一致性的分散化控制方法对于作动执行机构失效具有一定容错性。

3 仿真分析

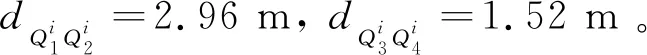
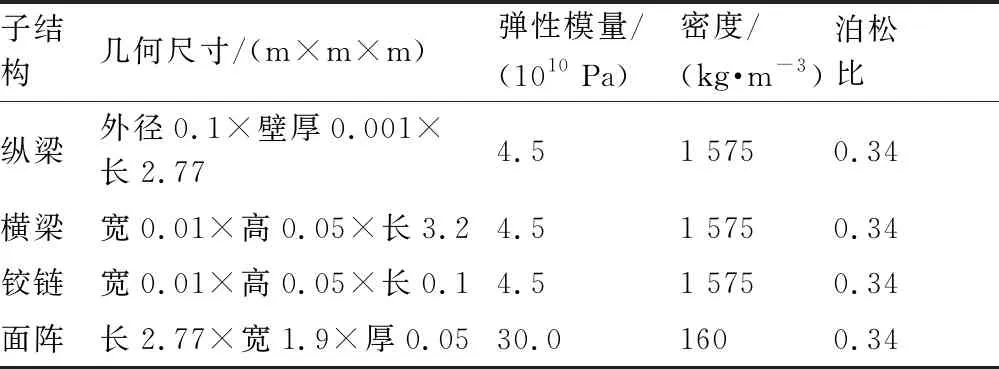
表1 单个子结构参数

根据式(5),分别求得由18节子结构的纵梁与横梁构成支撑桁架、面阵的前10阶模态频率与模态振型,进一步根据动力学方程,代入支撑桁架与面阵连接界面的位移协调条件(铰链约束关系),建立18个子结构组成的桁架式天线线性部分的8阶模态方程,模态频率分别为0.094 9、0.631 9、0.921 3、0.936 1、1.229 7、1.552 7、1.903 3、2.280 6 Hz,阻尼比为0.005。作动执行

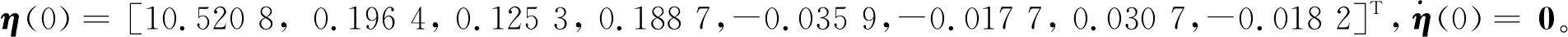
表示各控制子单元间关系的Laplacian矩阵为

(16)

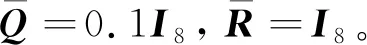
图2为桁架式天线自由衰减时,末端位移响应曲线与误差曲线。图3为应用所提分散协调控制方法的桁架式天线末端位移变化曲线。图4为选取其中的4个作动执行机构输出的控制力矩曲线。本文基于图论的一致性控制方法最大的优势是对作动执行机构的失效具有鲁棒性。图3(a)、图4(a)为12个作动执行机构完全有效时的情况；图3(b)、图4(b)为同样的干扰条件和控制参数下,假设12个作动执行机构中有4个完全失效时的仿真结果(节点62和节点232为其中2个失效的作动执行机构)。

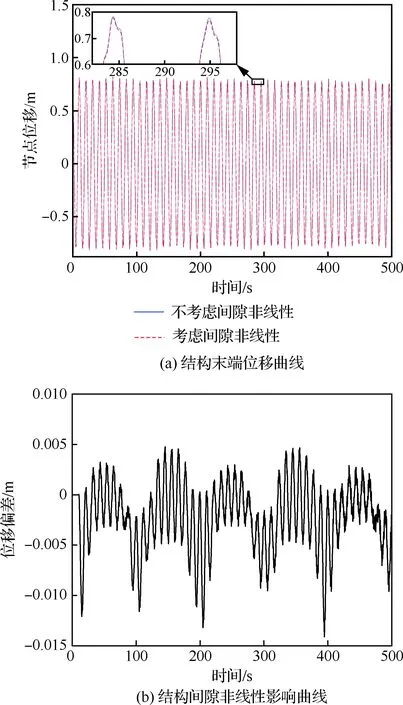
图2 桁架式天线末端的自由衰减位移响应曲线与误差曲线

从图3(a)、图4(a)可以看出,所提分散协调控制方法可以使考虑非线性连接的大型桁架式天线的振动快速衰减,在末端初始振动幅值为0.2 m 的条件下,约1 650 s后衰减至0.001 m以下,可满足天线在轨工作需求。对比图3(a)与图4(a)、图3(b)与图4(b)可以看出,末端实际形变量只存在微小的偏差,从2 000 s的总体变化来看,无明显变化,而从配置在这4个节点上的作动执行机构输出的控制力矩可以看出,由于节点62和节点232位置处的作动执行机构失效,故其输出控制力矩为0,而节点87和节点262位置处的未失效作动执行机构的控制力矩比原来稍大,但也未超出设定的100 N·m控制上限,仿真结果充分说明所提控制方法对于干扰和作动执行机构失效具有很好的鲁棒性。

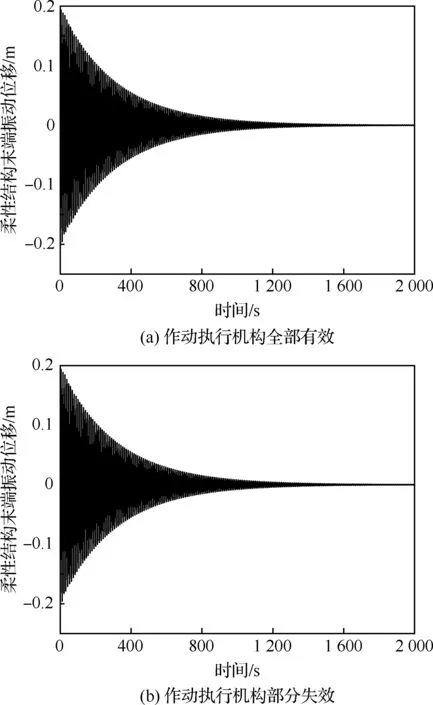
图3 基于一致性控制方法桁架式天线末端位移响应曲线

图4 基于一致性控制方法的作动执行机构控制力矩曲线

4 结 论

1) 针对带非线性连接的大型桁架式天线,采用连接子结构的模态综合法,将满足线性弹性理论的部分作为线性子结构进行建模,并将铰链作为非线性连接子结构进行建模,建立了大型桁架式天线的低维非线性动力学模型。

2) 提出了一种一致性分散协调控制方法,考虑了柔性结构分散化系统的一致协调控制问题,基于图论设计了柔性结构形面保持一致性控制器,不仅实现了柔性结构的高精度形面控制,同时也增加了系统的容错性和鲁棒性。