大气层内模型预测静态规划拦截中制导
周聪,闫晓东,*,唐硕,吕石
1.西北工业大学 航天学院,西安 710072
2.陕西省空天飞行器设计重点实验室,西安 710068
近年来,快速发展的高超声速武器系统对现有拦截系统造成极大挑战,一旦服役,必将打破原有战略平衡[1]。因此,世界各主要大国在加快进攻性高超声速武器的实战化步伐同时,也在大力发展高超声速武器防御技术,先进、有效的拦截制导方法是防御技术的关键之一[2]。与应对传统目标不同,中制导在此类目标拦截制导中被认为具有重要作用[3]:一是目标高机动以及轨迹难以预测的特性对中制导有效实施造成较大困难[4];二是在苛刻的拦截条件下,末制导以及最终拦截效果的实现更依赖中制导交班条件,对中制导交班精度与约束能力提出了更高的要求[5-6]。因此,针对此类目标的拦截中制导问题近年来得到了广泛关注与研究。目前,多种新型拦截中制导方法被提出,这些方法通过改善目标预测精度[7-8]、考虑更多约束[8-11]以及应用数值规划算法增强修偏能力[12-14]等方式来提高拦截高速机动目标的能力。但这些方法在设计时更多关注中末制导交班要求,且假定中制导启动时发动机已关机,对初制导段的飞行考虑较少。事实上,初制导段的飞行以及初中制导交班状态对后续中制导性能乃至拦截效果影响显著,而一般初制导所采用的预设程序转弯的方式很难保证能够提供较优的交班条件,也无法在目标机动时实时调整跟踪。尤其在面对具有较强机动能力的临近空间目标时,其灵活的机动形式和苛刻的拦截条件更要求精细化的初制导段以及初中制导交班条件设计,此时,将传统的初制导段纳入中制导范畴,进行联合一体化设计,不失为提高此类目标拦截能力的有效途径。
目前,针对这类初中制导结合的研究较少,文献[15]通过采用标准弹道族插值拟合的方法实现了全程的预测拦截制导。文献[16]考虑最大化射程要求,分别采用滑模和脉冲调制的方法设计了初制导和中制导,但实施起来较复杂,而且没有考虑制导的最优性。由于初、中制导一般对应拦截弹的动力段和滑行段[16],是一个典型的两段制导问题。而且动力段飞行时大气稠密,飞行状态变化剧烈,应用传统解析方法进行闭环制导设计时具有较大困难。近年来快速发展的凸优化[17]、模型预测静态规划(Model Predictive Static Programming, MPSP)[18]等在线优化方法为这类复杂制导问题解决提供了有力工具。其中,凸优化已广泛应用于各类制导问题中[19-21],模型预测静态规划算法作为另一类规划算法,相比凸优化方法具有更高的计算效率[22],而且其基于终端偏差修正的求解方式更易用于导弹制导问题中[13]。目前,MPSP算法在拦截中制导设计中已有所应用[12-13],但仍存在不足。例如只能使用控制量的二次型作为性能指标,将其直接应用于大气层内拦截问题时无法实现最大化终端速度的要求,影响拦截能力[12]。针对此问题,Kumar等提出了状态性能指标MPSP算法[23],通过优化减小阻力来实现最大化的终端速度,但其基于状态敏感矩阵构建的方式,不仅计算过程繁琐,而且将影响原有MPSP算法计算效率。此外,现有MPSP算法一般只能解决终端时间固定的单段制导问题,在应用时有诸多限制。
考虑到以上问题和需求,基于模型预测静态规划原理设计了一种初中制导联合规划制导方法。在进行中制导设计时,同时考虑了初始射向以及传统的初制导段,以最大化终端速度进行整体规划,提升拦截能力。所做的主要工作有:① 提 出了带初始状态规划以及复合状态性能指标的MPSP算法,相比原始MPSP[13]以及状态相关性能指标MPSP[23],在引入状态相关性能指标同时保持了原有MPSP算法计算效率,而且可以对初始状态进行优化;② 基于等效阻力建立了包含动力段与非动力的两段规划模型,通过采用分段离散以及构建关机点变分关系的方法,避免了内点约束的引入,使MPSP算法可直接求解;③ 结 合本文提出的MPSP算法以及两段规划模型,实现了终端速度最优的拦截轨迹规划;同时结合目标预测方法,实现了对机动目标的预测规划制导。仿真结果表明了本文方法的有效性。
1 问题描述与分析
1.1 拦截弹模型
地面发射坐标系下拦截弹的质点动力学方程为
(1)
(2)
(3)
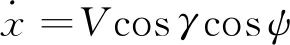
(4)
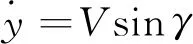
(5)
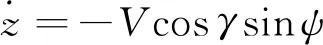
(6)
(7)
式中:V为速度;γ为弹道倾角;ψ为速度航向角;m为拦截弹质量;g为重力加速度;x、y、z为拦截弹在地面发射系下的位置;P、ms为发动机的推力和秒流量;α、β为拦截弹的攻角和侧滑角;X、Y和Z分别为拦截弹的阻力、升力和侧向力,定义为
X=qSCx(Ma,α,β)
(8)
Y=qSCy(Ma,α)
(9)
Z=qSCz(Ma,β)
(10)
其中:q为动压;S为参考面积;Ma为马赫数Cx、Cy、Cz分别表示导弹的阻力、升力、侧向力系数。
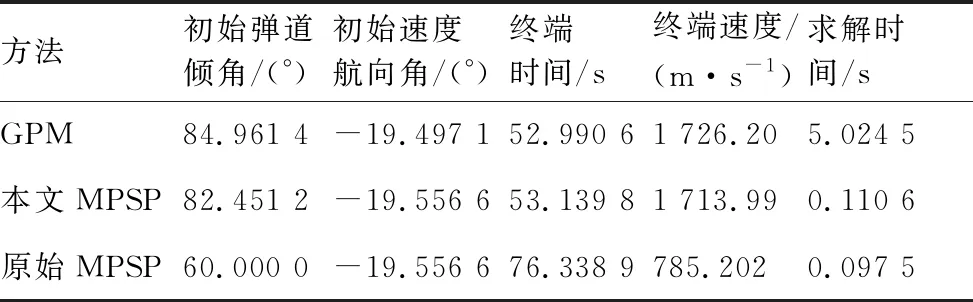
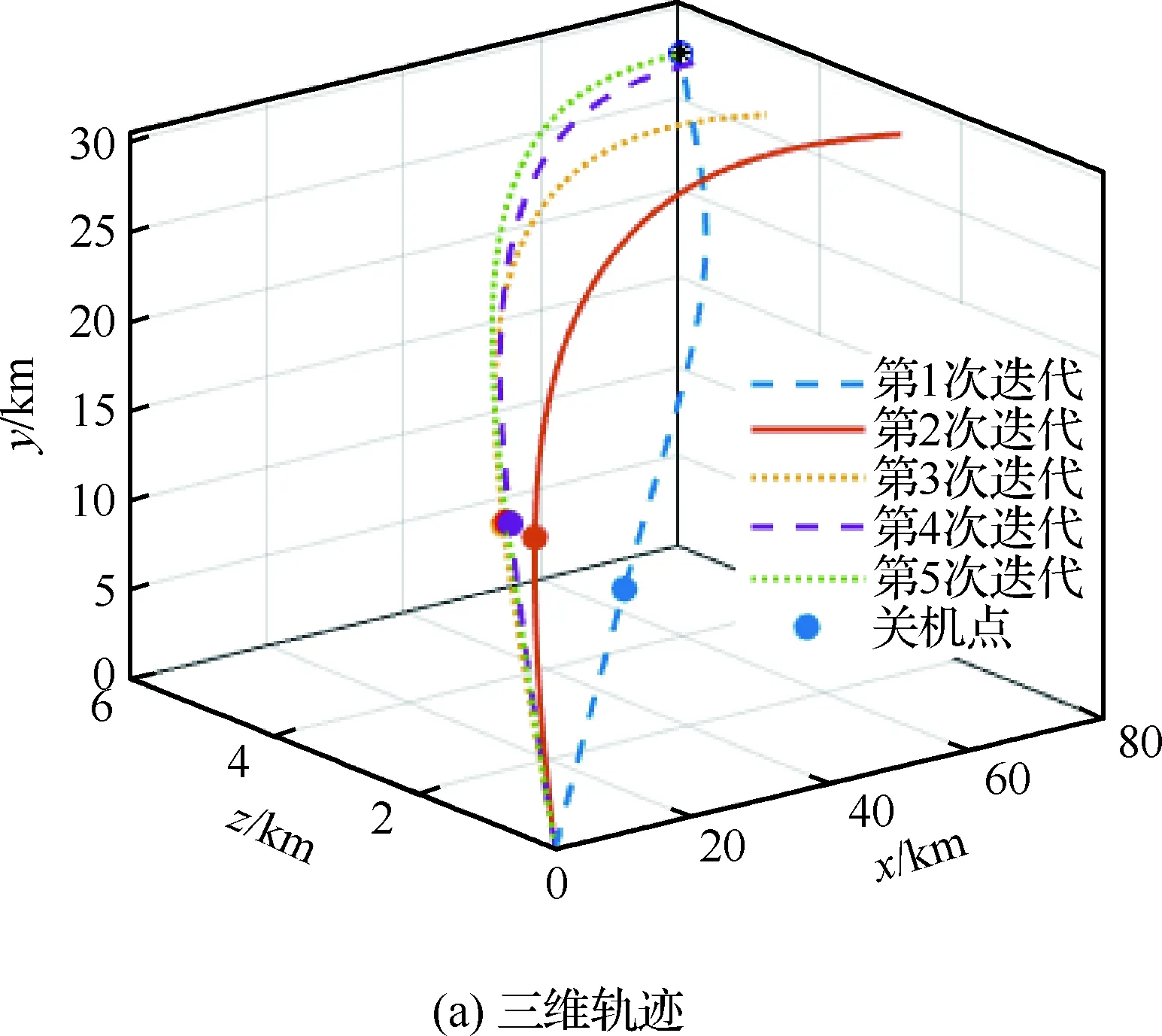
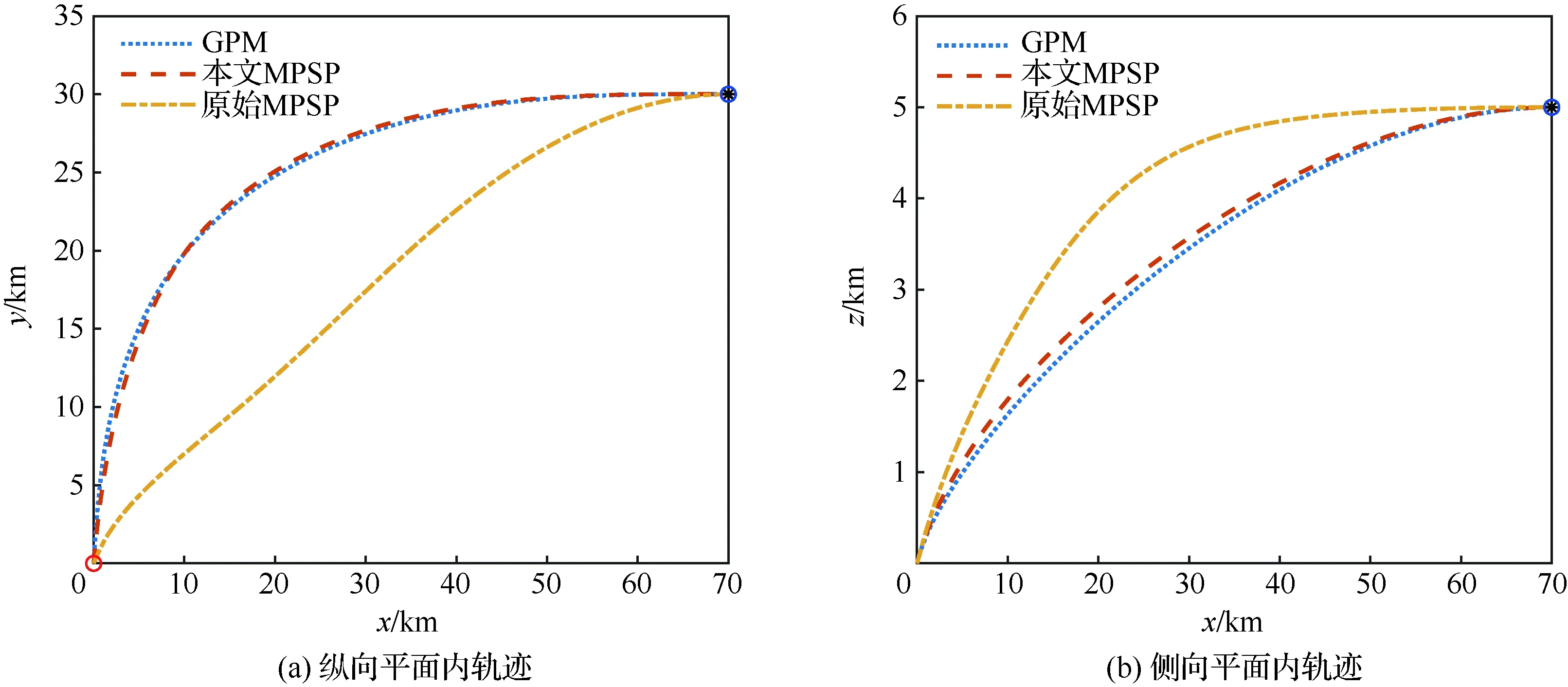
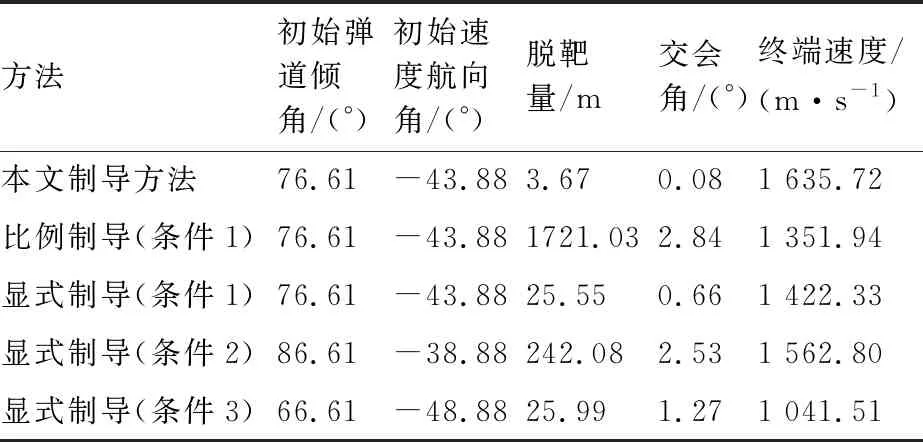
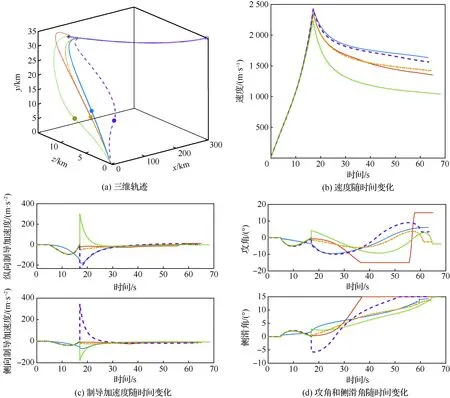
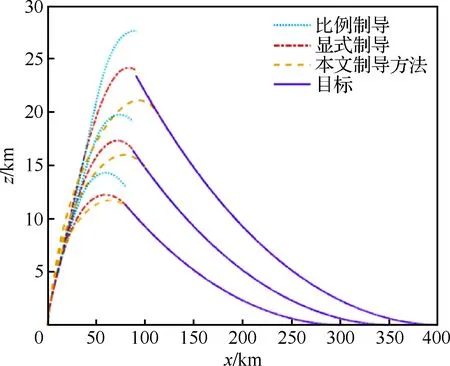
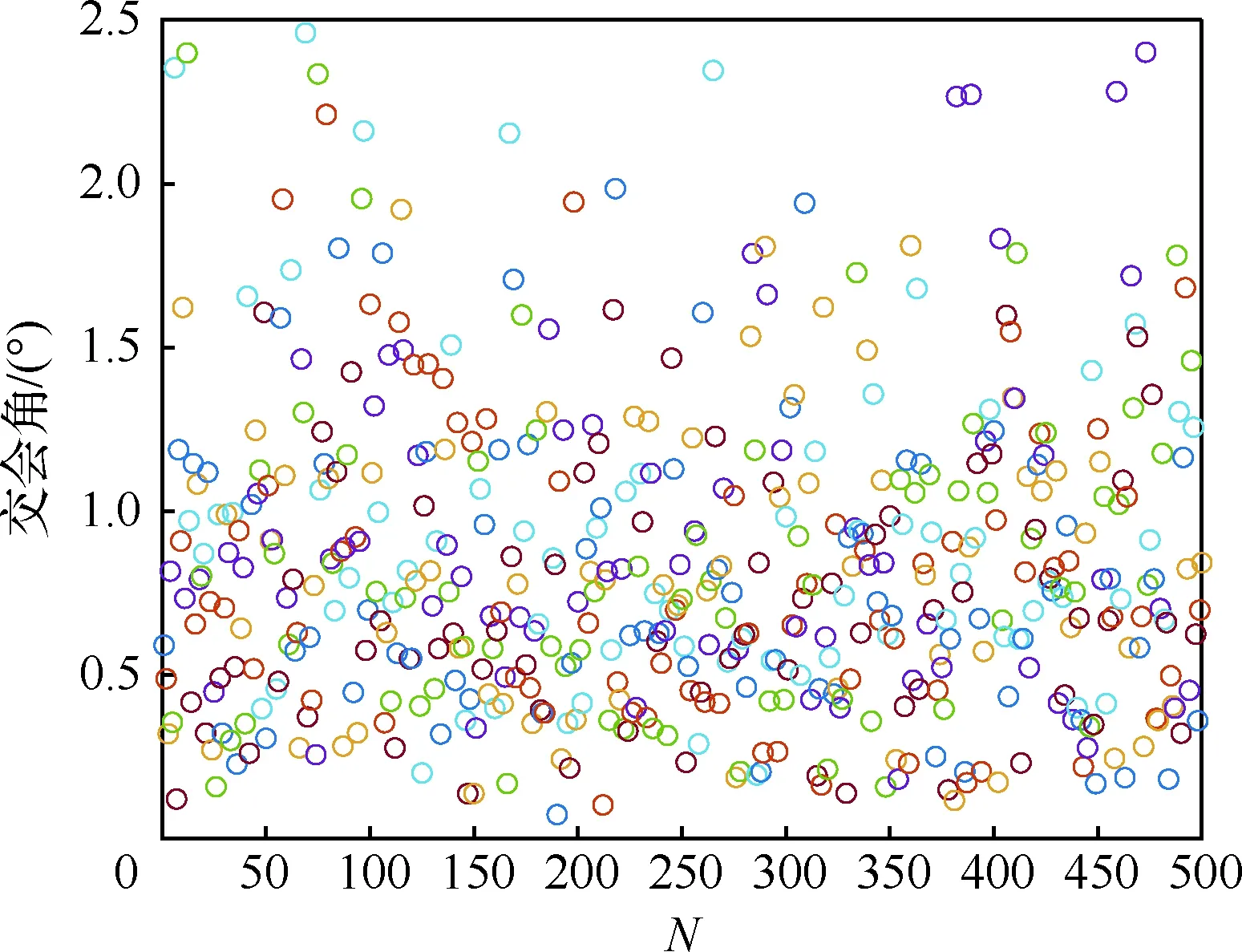
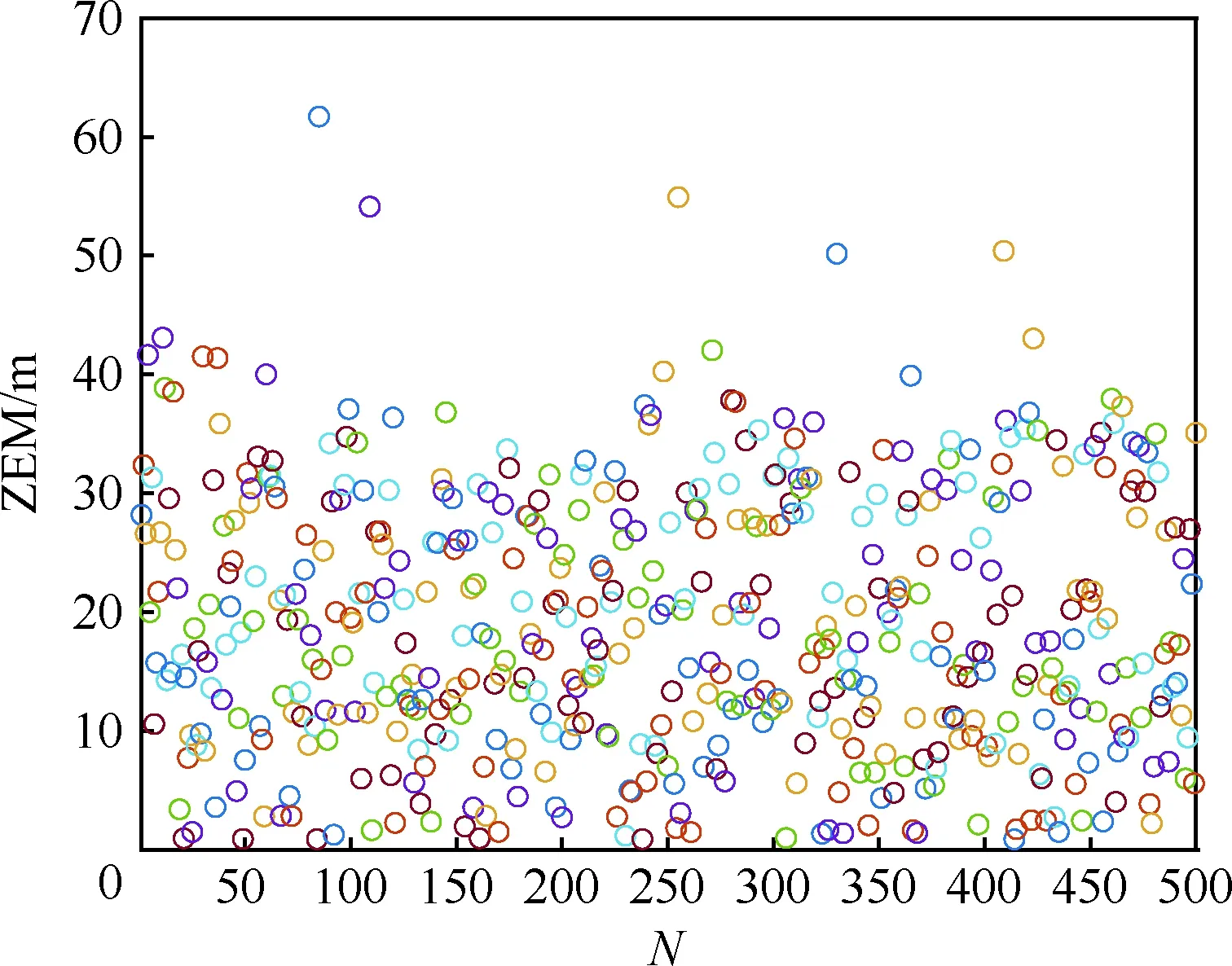
一般大气层内拦截弹采用单脉冲固体火箭发动机,其工作时间是固定的[16],整个飞行过程可分为动力段和无动力段(见图1)。假定其关机点时刻为t1f,则当t 图1 坐标系与拦截几何关系 (11) 拦截弹的纵侧向制导加速度分别由推力分量与气动力的合力提供: (12) 在动力段飞行时,由于有推力分量作用,可用制导加速度较为充足;而在滑行段时,制导加速度完全由气动力来提供,其大小受最大攻角和侧滑角限制: (13) 式中:Cymax、Czmax分别表示最大攻角和最大侧滑角下的升力和侧向力系数,其与马赫数有关。 中制导要求为末制导提供良好的初始条件,满足中末制导交班要求。在拦截高速机动目标时,除了约束终端脱靶量,还需要尽可能的减小交会角同时增大终端速度[6,8]。因此,中、末制导的交班条件可描述为 (14) max:V(tf) (15) 式中:(xf,yf,zf)为要求的预测拦截点位置坐标;(γf,ψf)为实现零交会角要求的终端弹道倾角和速度方向角;tf为终端拦截时刻。以上交班条件的实现,除了与中制导段飞行息息相关外,很大程度上还取决于初、中制导交班状态以及初制导段的飞行。 一般的,初、中制导分别对应拦截弹的动力段与滑行段[16]。令初、中制导段的制导加速度分别为[a1y,a1z]T, [a2y,a2z]T。为了保证拦截弹发射后飞行稳定,一般在初始飞行tc时间内采用零攻角方式,因此对于初制导加速度有: a1y(t (16) a1z(t (17) 此外,在实际拦截过程中拦截弹的射向(初始弹道倾角γ0和速度方位角ψ0)也将会对拦截效果和后续飞行带来较大影响。通过选择合理的初始状态,可以有效降低能量消耗。 综上所述,为了给末制导提供更好的初始状态,实现最优的交班的条件,需要考虑初始射向,初制导以及中制导段飞行,此问题可描述为:给出合理的初始状态[γ0,ψ0]以及初制导段和中制导段控制序列[a1y,a1z]T, [a2y,a2z]T,使其在满足式(13)式(14)以及式(16)和式(17)约束的条件下,最大化性能指标式(15)。 原始MPSP算法[13]一般用于解决固定初始条件,带终端约束最优控制问题,通常采用总控制量最省的性能指标: (18) 式中:Uk、Rk分别为第k离散步对应的控制量和控制权重。如前所述,对于大气内拦截问题,希望尽可能的增大终端速度,即需要减小飞行过程中的阻力。一般地,飞行器的阻力包括零升阻力和升致阻力两部分。当采用过载作为控制量时,应用如式(18)的性能指标可实现飞行过程中的升致阻力最小。但为了更好的实现最大化终端速度要求,还需要减少零升阻力。由于零升阻力主要与飞行状态相关(高度、速度),因此在规划时需要采用复合状态相关的性能指标;此外,为了选择合理的射向(初始弹道倾角和弹道偏角),需要对飞行器的初始状态进行优化。为了解决以上问题,提出了可进行初始状态规划,同时复合状态相关性能指标的改进MPSP算法。 改进的MPSP算法基于以下离散系统: Xk=Fk-1(Xk-1,Uk-1) (19) Yk=h(Xk) (20) 式中:Xk∈Rn,Uk∈Rm,Yk∈Rp分别为系统第k离散步下的状态矢量,控制矢量和输出矢量,且k=1,2,…,N。将系统的终端输出偏差ΔYN视为小量, 有: (21) 对式(19)进行泰勒展开,忽略高阶项,可得到第i离散步的状态偏差: (22) 同理可得第i-1,i-2,…,2离散步的状态偏差dXi-1,dXi-2,…,dX2,将其依次代入式(22),可得: (23) 式中:各系数矩阵为 (24) (25) 在原始MPSP算法中,不考虑初始状态偏差,即认为dX1=0。在这里考虑系统的若干初始状态Z=[z1,z2,…,zs]T∈X1可调,其中s≤n,此时令 (26) 相应的,式(23)可写为: (27) 若i=N,式(27)即表示终端状态偏差dXN。将其代入式(21),可得系统的输出偏差为 dYN=A0dZ+B1dU1…+BN-1dUN-1 (28) 式中: (29) A0,Bk即为可调初始状态量Z以及控制量Uk(k=1,2,…,N-1)对系统输出的敏感矩阵。 至此,获得了各离散时刻控制以及初始状态偏差与系统输出偏差的关系式(28)。MPSP算法的设计目标为同时迭代控制量Uk以及可调的初始状态Z,使系统输出趋向于要求值(YN→YNd),同时使以下复合系统状态相关的性能指标最优: (30) (31) (32) 此外,可调初始状态Z作为本文算法的另一迭代量有以下更新关系: Zp+1=Zp-dZ (33) 由此,可构建关于dZ和dUk(k=1,2,…,N-1)的静态规划问题,即在满足等式约束式(28)的同时使性能指标式(30)最小。此问题的增广拉格朗日函数为 (34) 式中:λ为拉格朗日算子,其一阶必要条件为 (35) (36) (37) 式中: (38) (39) (40) 因此,敏感矩阵hk和h′0的表达式为 (41) (42) 式中: (43) 获得以上敏感矩阵后,通过联立式(35)~式(37) 即可求解控制矢量和初始状态矢量的更新量dUk、 dZ。 首先由式(36)可得 (44) 将式(44)代入式(35),得 dYN-bλ-Aλ·λ-cλ-A0dZ=0 (45) 式中: (46) (47) (48) 此时,式(45)和式(37)可组成关于dZ和λ的线性方程组,令 有 W·X=N (49) 可解得 X=W-1·N (50) 由此,可得到dZ以及λ,将解得的λ代入式(44),即可求得dUk。 需要注意的是,若不考虑对初始状态Z优化,则矩阵A0、h′0、 dZp均为0,此时求解方程式(50)可得到复合状态性能指标下的控制矢量更新式: (51) 进一步的,若不复合状态相关性能指标,采用式(18)的性能指标形式,此时矩阵hk,cλ变为0,则控制矢量更新式(51)退化为 (52) 式(52)即为原始MPSP方法的控制矢量更新方法。 敏感矩阵计算是MPSP算法实施的关键,也是其计算耗时最多的部分[22]。为了提高计算效率,原始MPSP算法通过反向递归的方法计算敏感矩阵Bk[13]: (53) 式中:k=N-1,N-2,…,1,且当k=N-1时有 (54) 本文MPSP算法在实施时,除了Bk,还需要计算敏感矩阵A0、hk以及h′0。对于敏感矩阵A0,可在敏感矩阵Bk递归计算的基础上计算: (55) 而对于敏感矩阵hk和h′0,设计递归计算方法,首先令 (56) 则根据式(24)、式(25)及式(26),有 (57) 进一步地,令 (58) 根据定义,敏感矩阵hk和h′0可以表示为 (59) (60) (61) 为了应用本文MPSP算法求解如1.2节定义的规划问题,对式(1)~式(12)描述的动力学模型进行如下处理,首先令 Px=P(1-cosαcosβ) (62) Py=Psinα (63) Pz=Pcosαsinβ (64) 式中:Py、Pz分别表示导弹推力在纵向和侧向的分量,Px可理解为推力在速度方向的损失。此时拦截弹的纵向和侧向制导加速度可分别表示为 (65) (66) 分别应用式(62)、式(65)以及式(66),可将方程式(1)~式(3)改写为 (67) (68) (69) 式中: XD=Px+X (70) 将原动力学方程组中的式(1)~式(3)用式(67)~ 式(69)替换,同时加入时间t,可组成用于规划的动力学方程组: (71) 其中,状态向量X=[V,γ,ψ,x,y,z,m,t]T,控制向量U=[ay,az]T,XD可理解为导弹的等效阻力。为了应用此方程组,需要建立控制量[ay,az]与XD的关系: 首先考虑动力段,此时拦截弹的攻角,侧滑角均很小,式(65) 和式(66)可近似为 (72) (73) 式中: (74) (75) (76) (77) (78) 则式(75)和式(76)可写为 Py=c1·may,Y=c2·may (79) Pz=c1·maz,Z=c2·maz (80) 此时: (81) 应用阻力极曲线[22],可将拦截弹的阻力系数表示为 (82) 式中:Cx0为零升阻力系数,K为诱导阻力系数,其与马赫数有关。将式(82)代入式(8),同时结合式(79)和式(80),可将拦截弹的阻力表示为 (83) 式中: X0=Cx0·q·S (84) 将式(81)和式(83)分别代入式(70),整理可得: (85) 式中: (86) (87) (88) 模型预测静态规划算法基于固定自变量区间的离散模型,在实施时首先需要将原动力学方程离散化。对于一般的制导问题,由于终端时间不定,通常将导弹位置分量x作为离散自变量[14]。但本文规划轨迹包含了动力与不带动力的两段,如直接按位置分量x进行离散,由于关机点时刻位置不确定,将面临内点约束问题。考虑到动力段终端时间是确定的,而滑行段终端位置是确定,本文在求解两段轨迹规划问题时,采用混合离散的方法,即在动力段按时间离散,而在滑行段按导弹的位移分量进行离散,为此定义新的系统自变量: (89) 式中:t1f为关机点时刻,x1f为关机点位置的x坐标,x2f为拦截点位置x坐标。此时,动力段系统自变量τ∈[-1,0],而在无动力段τ∈[0,1]。 将规划方程(71)转化为以τ为自变量,首先令: (90) 定义权重量W=dt/dτ,同时由式(89)可得: (91) 则以τ为自变量的系统状态方程为 X′=f′(X,U,t)=f(X,U,t)·W (92) 对新的系统方程式(92)在区间τ∈[-1, 1]上离散,即可实现对原系统方程在动力段按时间离散以及滑行段按位移x离散的要求。一般地,采用欧拉离散,其离散方程可表示为 Fk(Xk,Uk)=Xk+f′(Xk,Uk,τk)·Δτ (93) (94) (95) (96) 在实际计算时,权重W中的x1f可取初始猜测或前次迭代得到的关机点时刻的导弹位移,即 x1f=x(t1f) (97) (98) 同时观察式(97),考虑到x1f仅由关机点时刻导弹状态决定,从而有 (99) 式中:ex=∂x/∂X=[0,0,0,1,0,0,0]。将式(99)代入式(98),可得 (100) (101) 基于3.1节和3.2节建立的离散规划模型,同时应用第2节介绍的MPSP算法,求解1.2节描述的两段轨迹规划问题。首先考虑拦截弹的初始弹道倾角和弹道偏角可调,即令Z=[γ,ψ]T;为了对终端脱靶量和交会角约束,定义系统输出为Y=[x,y,z,γ,ψ,]T。 本文轨迹规划的目标为终端速度最大,首先将终端速度近似为 (102) 式中:Δτ为离散步长。将式(67)和式(85)依次代入式(102),得 (103) Rk=(A2+A1)mW (104) (105) 此外,为了保证拦截弹发射后飞行稳定,确保在初始飞行tc时间内采用零攻角方式(即U(t Bk(k (106) (107) 其中,tkc=tc。 拦截高速机动目标时,需要采用预测制导的模式,即首先预估拦截点,然后引导导弹打击该拦截点。因此,为了应用本文方法拦截机动目标,需要结合目标预测方法。一般的,对目标状态的预测是基于目标当前状态(位置、速度、加速度等)和剩余飞行时间的,可将某一预测方法表示为 Y′T=fp(XT,tgo) (108) 式中:XT表示可获得的目标当前状态;tgo为剩余飞行时间;Y′T为预测的目标状态。 为了满足机动目标拦截以及交会角约束要求,预测方法需要给出拦截点处的目标位置以及航迹角,因此选择:Y′T=[x′T,y′T,z′T,γ′T,ψ′T]T。在实施时,将目标预测与MPSP方法的模型预测过程相结合:当MPSP算法采用数值积分方法逐时间步长tk计算导弹输出Y(tk)时,同步按照预测方程式(108)计算tk时刻(剩余飞行时间tgo=tk-t)的目标预测状态Y′T(tk),以及两者的脱靶量R(tk),直至R(tk) 图2 MPSP规划制导实施流程 采用这样的方式,MPSP方法在进行模型预测的同时即可估计预测拦截点状态,继而根据两者偏差规划实现对机动目标的预测拦截。由于MPSP方法在模型预测时采用了数值积分方法,相应的,目标预测方法式(109)可应用数值或解析形式。本文在实施时,采用文献[8]提出的圆弧预测方法,其需要的测量信息为多个历史时刻的目标位置。 通过数值仿真验证本文方法的实际效果,在实施时分为两部分:首先针对固定拦截点进行打击,验证本文MPSP方法的规划效果;然后以做侧向机动的CAV-H飞行器作为目标,验证本文MPSP方法结合目标预测后对机动目标的拦截能力。仿真时,滑行段可用过载由最大攻角和侧滑角α、β∈[-15°,15°]约束。 拦截弹的初始位置为(0, 0, 0) km,速度为15 m/s, 发动机工作时间17 s。给定的拦截点位置为(70, 30, 4) km,速度倾角和航向角约束均为0°。分别应用本文MPSP方法、原始MPSP方法以及高斯伪谱法(GPM)进行规划。其中在应用原始MPSP方法时,采用与本文方法一致的模型,控制量性能指标选择式(104)。由于原始MPSP方法不具备初始状态规划能力,在规划时初始速度航向角选择本文方法得到的结果,初始弹道倾角设为60°(其它值无法收敛)。在实施时,本文MPSP方法与原始MPSP方法在动力段与滑行段分别采用零控(U=[0,0]T)和比例制导作为初始猜测,终端脱靶量和角约束精度分别设为1 m和0.1°。各方法的规划结果如表1、图3~图4所示。 表1 针对固定点规划结果 图3给出了本文方法的规划迭代过程。可以 图3 本文MPSP方法规划结果 看到,经过5次迭代,其终端精度满足了要求。而且在迭代过程中,关机点和初始弹道倾角以及速度航向角进行了有效的调整,证明了本文方法以及所构建两段规划模型的有效。 图4给出了3种方法的规划结果对比。可以看出,本文MPSP方法规划得到的结果非常接近高斯伪谱法(GPM)给出的最优解,其终端速度(1 713.99 m/s)仅比高斯伪谱法得到的结果小12 m/s,而且两者得到的初始射向(如表1 所示),轨迹形式(图4(a)~图4(d))和加速度曲线(图4(e)~图4(f))也较为接近。相比之下,应用原始MPSP方法规划时出现了较大的速度损失,其终端速度(785.2 m/s)远小于速度最优解,轨迹形式和加速度剖面也显著不同于本文方法和最优解。导致这一差异的主要原因为原始MPSP算法所采用二次型性能指标形式(18),无法在其中引入零升阻力项。在这样的优化目标下,算法只能最大程度的减小升致阻力,如图4(e)~图4(f) 所示,其生成的制导加速度明显小于最优解,甚至在后半段直接令加速度为0,同时飞行时间也大幅度增加。这样的控制策略可以有效减小升致阻力(制导加速度由升力提供,与升致阻力正相关),但却使零升阻力的消耗大幅增加,从而导致了显著的速度损失(如图4(c) 所示)。显然,这样的速度损失将极大影响拦截能力。此外,本文MPSP算法在实施时相比原始MPSP算法仅增加13%的计算时间,远小于高斯伪谱法(如表1 所示)。其主要得益于一系列敏感矩阵递归计算设计,证明了算法的高效以及在线应用的可行性。 图4 针对固定拦截点的规划结果 以上结果和分析表明,零升阻力对大气层内拦截弹的飞行速度具有显著影响。应用原始MPSP算法进行规划时,由于在性能指标中不能考虑零升阻力,终端速度的最优性很难实现。而本文MPSP方法通过在性能指标中构建状态相关量以及构建终端速度最优的两段规划模型,在保持原有MPSP算法计算效率下,可得到接近最优解的结果,从而大幅提升终端速度,保证拦截弹具备良好的拦截能力 选择CAV-H飞行器作为机动目标,其初始时刻位置(300, 35, 0) km,高度 35 km,速度3500 m/s,速度倾角和航向角均为0°。在仿真时,CAV-H以恒定的攻角和倾侧角(α=10°,σ=40°)进行侧向机动,模拟其滑翔段的飞行方式。由于没有考虑末制导段,假定距目标 15 km时中制导结束,随后保持当前指令,以最终脱靶量和交会角为制导性能指标。其余初始状态和仿真条件沿用4.1节设置。 为了进行制导性能对比,分别应用本文提出的方法、比例制导以及变系数显式制导[8]进行仿真分析,均采用圆弧预测方法[8]进行目标预测。在实施本文方法时,首先应用本文带初始状态规划的MPSP算法(式(50))规划得到最优的初始弹道倾角和航向角,然后以此作为仿真初始条件采用不含初始状态规划的算法(式(51))进行制导。由于比例制导和显式制导一般只能用于无动力段,故动力段采用程序转弯方式[24],其转弯参数通过调制得到,初始弹道倾角和航向角选择本文方法给出的最优解。在实施时,首先调制出一组较优的程序转弯参数(条件1)应用于比例制导和显式制导,然后通过改变初始弹道倾角和偏角生成不同的关机点条件(如表2 所示,对应条件2,3)应用于显式制导以展示不同关机点条件对拦截效果的影响。 本文方法、比例制导以及不同关机点条件下显式制导的拦截结果如表2 和图5 所示, 可以看出:由于未加入末制导段修正,本文方法脱靶量和终端交会角没有完全收敛到0,然而其精度和终端速度显著高于比例制导和显式制导,且足以满足中末制导交班要求。作为对比,比例制导出现了较大的脱靶量,其主要是没有考虑可用过载约束,制导加速度饱和导致的[8]。当采用显式制导时,通过在初制导段选择合适的初始射向,调制合理的转弯参数(条件1),其精度也可以满足交班要求。但这一拦截效果的实现很大程度上依赖于初制导段良好的初始射向和飞行状态,如表2 所示,当调整初始弹道倾角和速度航向角使其关机点参数偏离调制所得到的较优条件(条件1)后,其拦截精度出现了较大程度下降(条件2),或是终端速度出现了较大程度的损失(条件3),而且其所需的制导加速度也出现了较大程度的增加(如图5 (c) 所示)。结果表明,初中制导交班条件对拦截效果具有较大影响,当在初制导段应用传统的程序转弯方式时,需要合理设计才能保证拦截效果。但在实际中这一要求并不容易达到,尤其考虑到临近空间目标灵活多变的机动特性和对拦截系统快速反应的要求。而本文所提出结合目标预测,采用MPSP进行初中制导联合规划制导的方法,不仅可以根据目标当前状态实时调整规划,而且可以实现更高的终端速度与精度。此外,结合MPSP方法进行预测拦截点估计时,由于直接应用了拦截弹非线性模型,可以考虑拦截弹速度变化,因此相比传统方法可以获得更高的预测精度(如图5(e)和图5(f) 所示),而预测精度的提升同样有助于提高拦截精度。 表2 机动目标拦截结果 图5 针对机动目标拦截轨迹 进一步地,在前述仿真条件的基础上,将目标初始位置依次设置为距发射阵地 350 km和 400 km 实施仿真。此时相比原有条件(距发射阵地 300 km),目标将实现更大的机动航程和机动横程(图6),相应的拦截结果如表3所示。与表2 表3 不同机动范围下目标拦截结果 图6 针对不同机动范围目标的侧向拦截轨迹 结果对比可以看到,随着目标侧向机动距离增大,比例制导和显式制导的拦截精度和终端速度显著下降,当目标初始位置为(400,0,0)km时已无法满足中末制导交班要求。而本文方法依然能实现较好的终端精度和终端速度,满足中末制导交班要求。结果表明,本文方法具备拦截更大机动范围目标能力,更能满足机动目标拦截的要求。 为了验证本文方法在测量信息不准确和参数偏差条件下的制导效果,在5.2仿真条件基础上,加入测量信息和气动参数偏差进行蒙特卡洛打靶仿真。其中,假定目标位置(x,y,z)和速度(Vx,Vy,Vz)分别含有一倍标准差为 50 m和 30 m/s的测量偏差[25],拦截弹的气动系数按三倍标准差为15%的偏差限摄动,仿真次数500。打靶统计结果如表4,图7以及图8所示。 图7 交会角分布图 图8 脱靶量(ZEM)分布图 表4 蒙特卡洛仿真统计结果 可以看到,加入随机偏差后,本文方法得到的零控脱靶量和交会角相比无测量偏差条件下均有所增大,其主要是由于位置偏差导致预测拦截点变化引起的。考虑到未加入末制导段修正,这样的精度与散布仍然能够满足中末制导交班要求。结果表明,在测量信息和气动参数存在随机偏差条件下,本文方法依然能够保持较好的预测和制导性能,且零控脱靶量和交会角可以满足中末制导交班要求。 1) 零升阻力对大气层内拦截弹的飞行速度具有显著影响,MPSP算法在规划时通过考虑状态相关性能指标引入零升阻力,可有效提升终端速度和拦截能力。 2) 在中制导设计时,通过考虑拦截弹的射向以及初制导段,进行联合规划,不仅可以提高导弹终端速度和制导精度,而且更能满足机动目标拦截的要求。 3) 测量不准确和气动参数不确定条件下,基于MPSP规划制导方法依然能够保持较好的制导性能,满足中末制导交班要求。 4) 带初始状态规划和复合状态相关性能指标的MPSP算法,以及所采用的两段规划模型的构建方法可用于其他制导问题。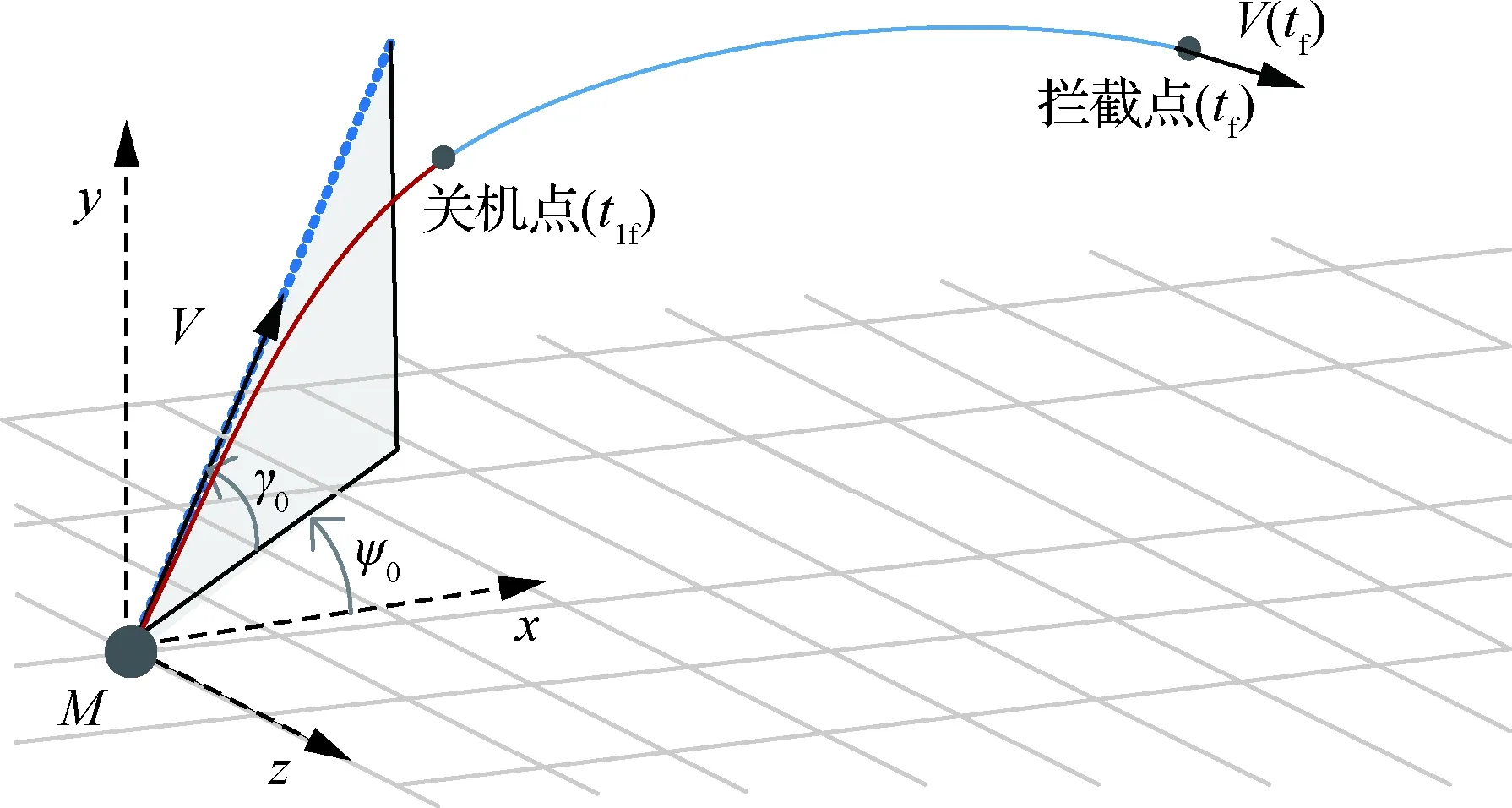
1.2 初、中制导联合轨迹规划与制导问题
2 改进的MPSP算法
2.1 带初始状态规划和状态性能指标的MPSP算法
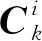
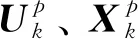
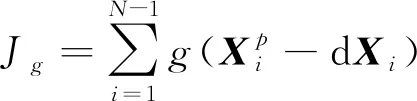
2.2 敏感矩阵计算方法
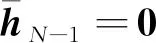
3 初、中制导轨迹联合规划
3.1 两阶段规划模型
3.2 方程离散化

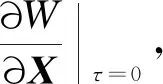
3.3 初、中制导轨迹联合规划
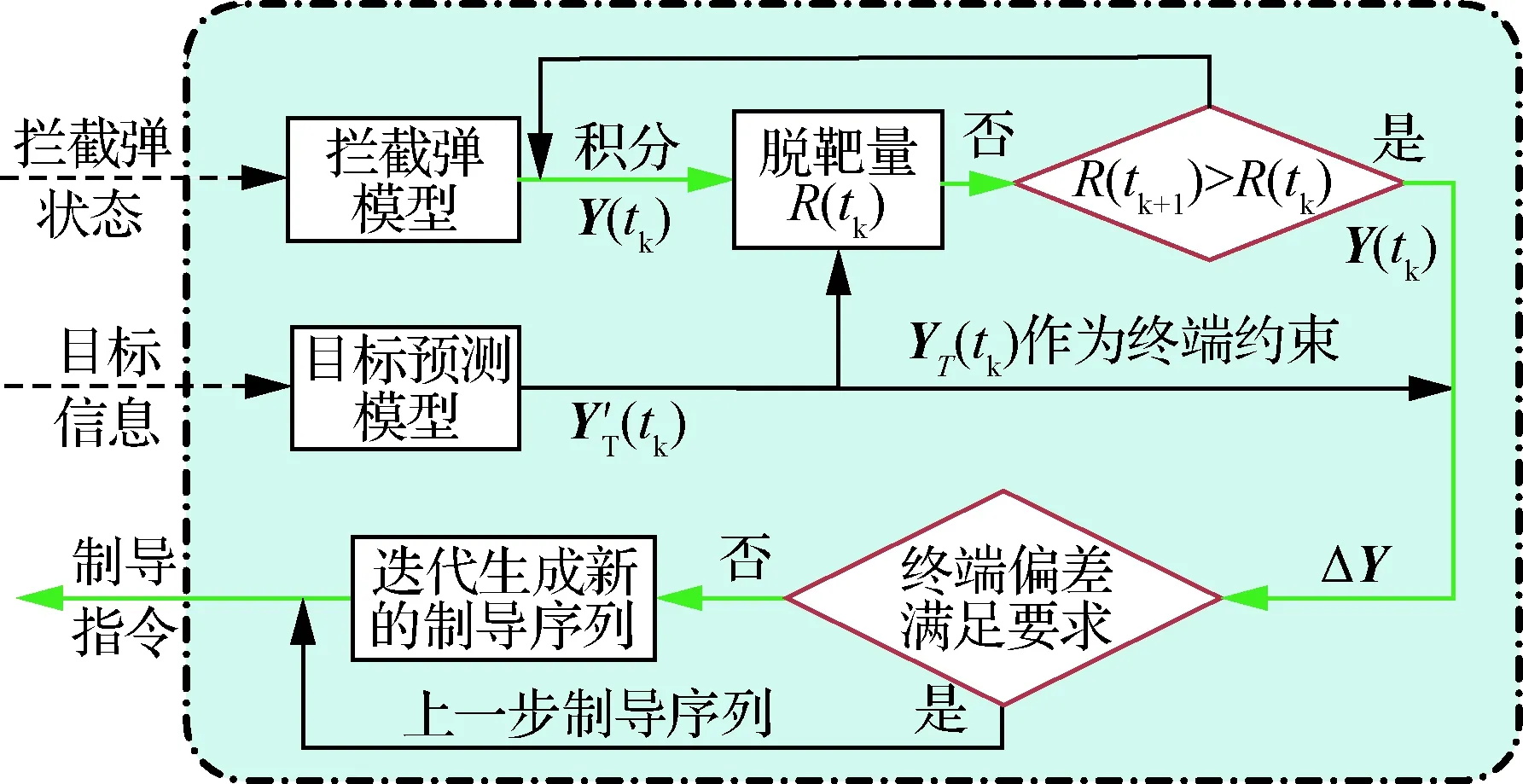
3.4 结合目标预测的规划制导方法
4 数值仿真与分析
4.1 针对固定拦截点规划结果
4.2 针对机动目标拦截制导结果


5 结 论

