基于NURBS曲面的三维人脸表情合成算法*

伍 菲

(桂林电子科技大学 信息科技学院， 广西 桂林 541004)

随着人工智能领域的快速发展，计算机视觉已成为该领域的热门研究方向.在技术研究逐渐深入的背景下，如何合成三维的人脸表情，成为了计算机视觉领域的重点研究方向[1-3]，具有较高的实用与商业价值.一般而言，三维人脸表情的合成是利用图片或视频中的数据，令中性参考模型生成丰富的表情变化.在不同光线、视角和角度等条件下，合成算法需对二维图片进行精细地刻画和优化[4-8].目前，大量学者已在三维人脸表情合成研究上取得了一定的成果[9-10].其中，Zhu等[11]使用BFM数据库和线性基，实现了三维人脸表情形状的生成；而Xiong等[12]在人脸表情生成过程中，引入了迁移方法，从而优化了算法的速度和执行效率.但人脸表情生成的研究领域仍有大量问题未被完全解决，例如：中性参考模型的选择，光线、角度和姿态等条件的影响，对应关系的选择及特征点位置的平滑性优化等.因此，如何设计一种适应多种背景条件且具有泛化性的通用算法，仍是三维人脸表情合成中急需解决的关键问题.

针对上述问题，本文在分析主流合成算法的基础上，提出了一种基于NURBS(non-uniform rational B-splines)曲面的人脸表情合成算法.该合成算法利用优化NURBS控制点的方法，确定连续的参考模型，同时该合成算法利用几何与平滑约束的方法，增加三维人脸表情的平滑性；通过相应的设置和优化，该合成算法部分消除了不同光线、角度和视角等条件的影响，从而得到更为优秀的三维人脸表情结果.

1 人脸建模

NURBS曲面是NURBS曲线由一维推广到二维运算的方法，具有局部可修改的特性，能够定义不均匀的节点间隔，因此，NURBS曲面可以刻画复杂的人脸几何结构.令参考模型M表示维度为a×b的NURBS曲面，P={Pi，j}m×n表示曲面中的控制点，U={ui}(1≤i≤m+a)与V={vj}(1≤j≤n+b)分别表示u和v方向上的节点向量，则参考模型可表示为

(1)

式中：Ni(u)、Nj(v)为样条基函数；w为非负数权因子.由于NURBS曲面理论能够定义不均匀的节点间隔，所以这里设定非负数权因子w=1.为了简化计算过程，本文将式(1)转化为矩阵运算，即

M(u，v)=Ru，v[Bx|ByBz]

式中：Ru，v为1×mn维的矩阵；Bx、By和Bz为控制点矩阵B的各个列向量，其维度均为mn×1.

2 三维人脸表情合成

利用NURBS理论可以确定人脸的中性参考模型，为了在参考模型中增加表情效果，本文需要利用人脸特征点来调节参考模型，同时增加几何和平滑约束，最终合成具有较高平滑度的三维人脸表情.

2.1 单视角模型

为了合成平滑的三维人脸表情，本文使用文献[13]中的人脸特征点检测算法，在二维图片和参考模型之间，提取准确的人脸特征点，并建立特征点集合之间的稀疏对应关系.根据二维图片与三维模型之间特征点的稀疏对应关系，令Ap表示维度为72×mn的特征点系数矩阵，Bn表示维度为mn×3的控制点矩阵，Qn表示二维图片对应的三维特征点，Tg表示整体的几何约束矢量，Ts表示局部的平滑约束矢量，λ和θ分别表示这两种约束的系数，单视角模型可表示为

(2)

2.2 约束条件

当求解迭代控制点Bn时，未知数个数大于方程个数，这意味着人脸的非特征点缺少必要的约束，所以，人脸表情合成过程中需要增加整体几何约束Tg和局部平滑约束Ts.

1) 几何约束.为克服人脸非特征点缺少约束的缺点，本文在参考模型中增加了基于二阶偏导的几何约束，其表达式为

(3)

式中：Bo为上一轮迭代的控制点；L2为z对于x与y求偏导数的和矩阵.令c表示NURBS曲面控制点的个数，则L2的维度为c×mn.若ru和rv表示维度为a×m与b×n的配置矩阵，则x、y和z的表达式为

(4)

需要说明的是，式(4)中Bx、By和Bz的维度均为m×n，由控制点矩阵B重排获得.利用z对x和y的二阶偏导数的几何与物理意义，本文可以确保人脸表情合成形状不出现非特征点噪声，从而增加合成结果的平滑性.

2) 平滑约束.为了降低稀疏对应关系产生的噪声，本文利用高斯权重法设计局部控制点的平滑约束，其计算表达式为

(5)

式中：B′o为中性参考模型的初始控制点；矩阵G的维度为c×mn.

通过增加高斯权重的平滑约束，算法可以调节特征点及其周边区域，避免人脸特征点变成奇异点，从而增加合成结果的平滑性.

单视角的模型进一步可表示为

(6)

对式(6)求导，令导数等于0，可得模型的最小值，即

(7)

式中，pinv为求伪逆矩阵的运算.

2.3 嘴部拟合

在人脸表情发生变化时，嘴部形状经常会比其他脸部位变化更大，因此，如何精细地拟合嘴部的轮廓，直接决定了三维人脸表情合成的视觉效果.为了更好地拟合嘴部轮廓，本文主要使用两种方式：1)增加嘴部特征点的数量和密度；2)提高NURBS曲线控制点的计算精度.按照此思路，文中使用的形式化模型表达式为

(8)

式中：Ap-m为维度是16×l的特征点系数矩阵，Ap-m每一个行向量均是一个嘴部特征点的特征点系数，l为控制点个数；Bn-m为维度是l×3的控制点矩阵；Qn-m为与二维图片具有对应关系的三维嘴部特征点集合.与式(5)的求解过程类似，对式(8)求导，当导数为0时得到最小值，即

(9)

3 仿真与分析

为了验证合成算法的有效性和泛化性，本文设计了相应的实验.该实验使用文中提出的人脸表情合成算法，将不同环境和光照条件的二维图片合成为三维的人脸表情形状，其合成前后的效果如表1所示.需要说明的是，本文的实验图片是一张合成图片，来自于文献[11].在迭代过程中，为了达到最优的实验效果，本文设定窗口尺寸W=7，权值系数λ=0.000 001，θ=1，方差δ=2.023.

在表1中，第1列图片是实验的原始图片，其中前4张是在不同的角度和姿势条件下拍摄的，后2张是在不同的光照条件下拍摄；第2列与第3列的图片分别展示了合成之后的平面和侧面的三维人脸形状；第4列图片展示了无纹理的合成形状.根据表1第2～4列所展示的图片可知，其人脸表情形状几乎无较大区别，这证明本文的合成算法具有较好的稳定性.

表1 合成前后效果对比图

由表1可知，本文合成算法可以重建出与输入图片一致的三维人脸表情，但表1展示的图片并未能衡量合成算法的重建准确程度.为了证明该合成算法重建准确度，本文将合成算法与文献[11]中的参考模型的多项运行结果进行了数据对比，其比较的项目分别是欧氏距离与均方根距离的均值，对比结果如表2所示.

欧氏距离与均方根距离的均值大小可以衡量三维人脸形状的准确度，即当这两个均值越小时，三维人脸形状越接近输入图片[13].其中，欧氏距离均值的计算方式为：首先计算合成的人脸形状特征点到输入图片最近点的距离；其次将该距离除以两点之间距离，完成标准化；最后对标准化之后的所有距离求均值.均方根距离均值的计算方

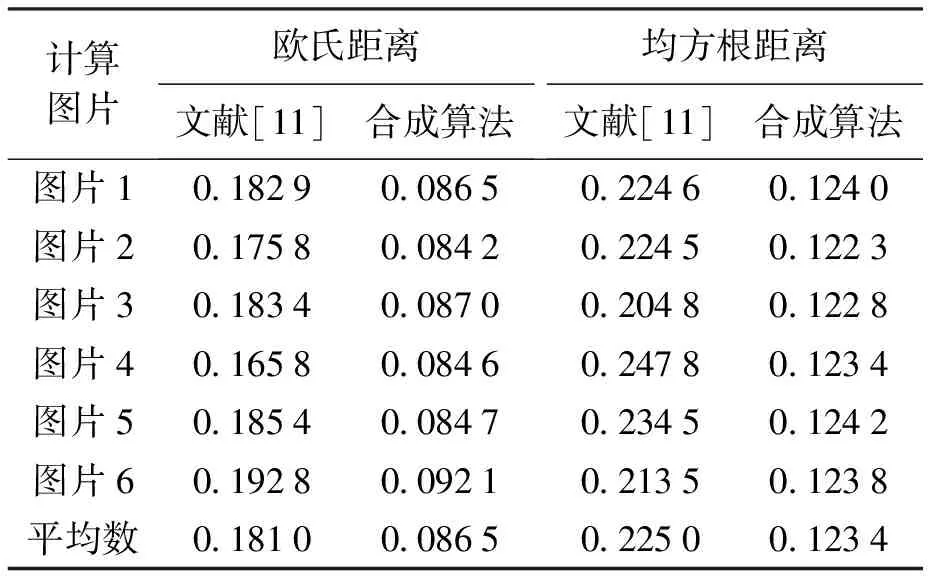
表2 文献[11]与合成算法重建结果对比Tab.2 Comparison of reconstruction results between reference [11] and synthesis algorithm

式为：首先使用合成特征点到最近点的距离减去欧氏距离，再求平方；其次，计算平方和，除以特征点总数；最后开方得到均方根距离.

根据表2可知，本文合成算法的欧氏距离和均方根距离的数值均小于文献[11]的相关参数.由参数的物理意义可知，本文合成算法重建效果优于文献[11]，具有一定的借鉴和参考价值.

4 结 论

基于NURBS曲面拟合与人脸特征点提取技术，并利用平滑约束和几何约束方法，本文提出了一种三维人脸表情合成算法.同时，本文对该算法进行了相关的仿真与分析，结果表明，该算法具有一定的稳定性和泛化性.但该算法的合成效果依旧不理想，仍存在较大的优化空间，尤其是在嘴部拟合部分，这也是未来的研究方向.