基于视觉原理的斜齿轮几何参数测量方法研究*

李 捷,刘 永,李昊泽,王 宸

(湖北汽车工业学院 机械工程学院,湖北 十堰 442002)

0 引 言

齿轮是机械传动领域中最为常见的机械零件之一[1]。随着现代工业的发展,对齿轮参数的在线测量方法和手段也越来越多。由于齿轮的几何参数较多,采用传统的测量技术已经无法满足现代工业领域自动、快速测量的需求。

作为一种全新的非接触式测量手段,视觉测量技术[2]具备测量精度及自动化程度高、操作方便等优点,现已被广泛地应用于汽车制造等工业领域中。

齿轮的参数较多,传统的手动及专用检测设备已无法满足自动、快速的在线测量需求。目前,不少学者基于视觉原理对齿轮的几何参数及相关误差进行了测量。

王文成[3]设计了一种基于机器视觉的测量系统,来对齿轮参数进行测量;但是该系统未能校正镜头所产生的畸变,导致齿轮图像出现失真,进而影响了其测量精度。程敏杰[4]采用最小外接矩形方法,测量了齿轮的齿顶圆直径,并将矩形边长的平均值作为齿顶圆的直径;但是该方法的测量结果容易受到齿轮边缘检测精度的影响,检测精度不高时,矩形与齿轮接触的点不一定真正在齿轮齿顶圆上,导致测量结果存在较大的误差。陈顺[5]、涂盼盼[6]采用改进的数学形态学边缘检测算法,提取到了更加完整、清晰的齿轮边缘轮廓;虽然该方法提高了齿轮的边缘检测精度,但是该研究没有涉及对齿轮的几何参数进行测量。王延忠[7]采用重心法对齿轮中心点坐标进行了测量,该方法效率高、操作方便;但是重心法只适用于对不带键槽的齿轮进行测量,采用重心法去测量带键槽的齿轮,会导致测量结果出现较大偏差。GADELMAWLA E S[8]采用边缘检测技术得到齿轮的轮廓曲线后,分别提取了齿顶和齿根圆弧部分的轮廓曲线,并采用最小二乘法拟合得到了齿顶圆、齿根圆的半径;该方法虽然计算量较小,但其数据较少,而且测量结果会受到轮廓曲线提取效果的影响,尤其是当轮廓曲线提取偏差较大时,其拟合结果也会存在较大的误差。WU W[9]计算了齿廓边缘点到中心点的距离值,并绘制了相关曲线图,通过计算图中波峰的数目来得到齿数;虽然该方法测量准确、效率高,但该研究在完成对齿数的测量后,未能利用曲线图信息测量齿轮齿顶圆、齿根圆半径等几何参数。

在研究了已有的齿轮几何参数视觉测量文献基础上,笔者提出一种基于视觉原理的斜齿轮几何参数测量方法。该方法首先采用槽型柔性组合夹具定位块将斜齿轮定位,并保证齿轮和相机的中心一致;其次,利用中值滤波等方法对采集的图像进行预处理,得到齿轮轮廓非零像素点坐标值;然后,采用最小二乘法拟合中心点坐标和中心孔半径,计算每个齿廓边缘点到中心点的距离值,并绘制成相关曲线图,通过曲线图信息来测量齿顶圆、齿根圆半径和齿数;随后,用Hough变换和两直线夹角公式来计算螺旋角,利用齿顶圆直径、齿数及螺旋角的相关公式,计算得到分度圆直径和模数值;最后,笔者利用最小二乘法拟合直线,通过计算得到键槽的尺寸。

1 测量系统构成及测量流程

1.1 测量系统构成

此处的测量系统[10]硬件装置采用维视智造公司研发的机器视觉教学研究创新实验平台(型号MV-VS1200S),主要包括工业相机、镜头、环形光源、工作台、槽型柔性组合夹具和计算机等。

计算机操作系统为Windows 10中文版,内存16 GB,处理器为AMD Ryzen 5 4600H with Radeon Graphics 3.00 GHz, MATLAB版本为R2020a。

相机型号为MV-EM120C,覆盖1.4×107pixels。镜头为BT-MPX系列(BT-MPX系列镜头有多种光学校正方式,具有低畸变率、低照度大通光孔径、高性能等特点,可最大限度地减少像差)。相机通过螺栓安装在支架上,高度可通过手轮调节,支架可移动,相机拍摄角度也可调节。

夹具通过螺栓固定在工作台上,利用槽型柔性组合夹具定位块,可将斜齿轮调整固定,经过多次调整相机、工件和夹具中定位键的位置,来保证齿轮和相机的中心一致(此时可最大程度减小畸变)。

测量时笔者将斜齿轮装夹固定,将采集到的图像传输到计算机上,通过计算机中MATLAB软件对图像进行处理,测量出斜齿轮相关几何参数。

测量系统整体构成如图1所示。

图1 测量系统构成图

1.2 测量流程

测量流程主要包括:图像采集、相机标定、重复性精度测试、图像预处理等部分,如图2所示。

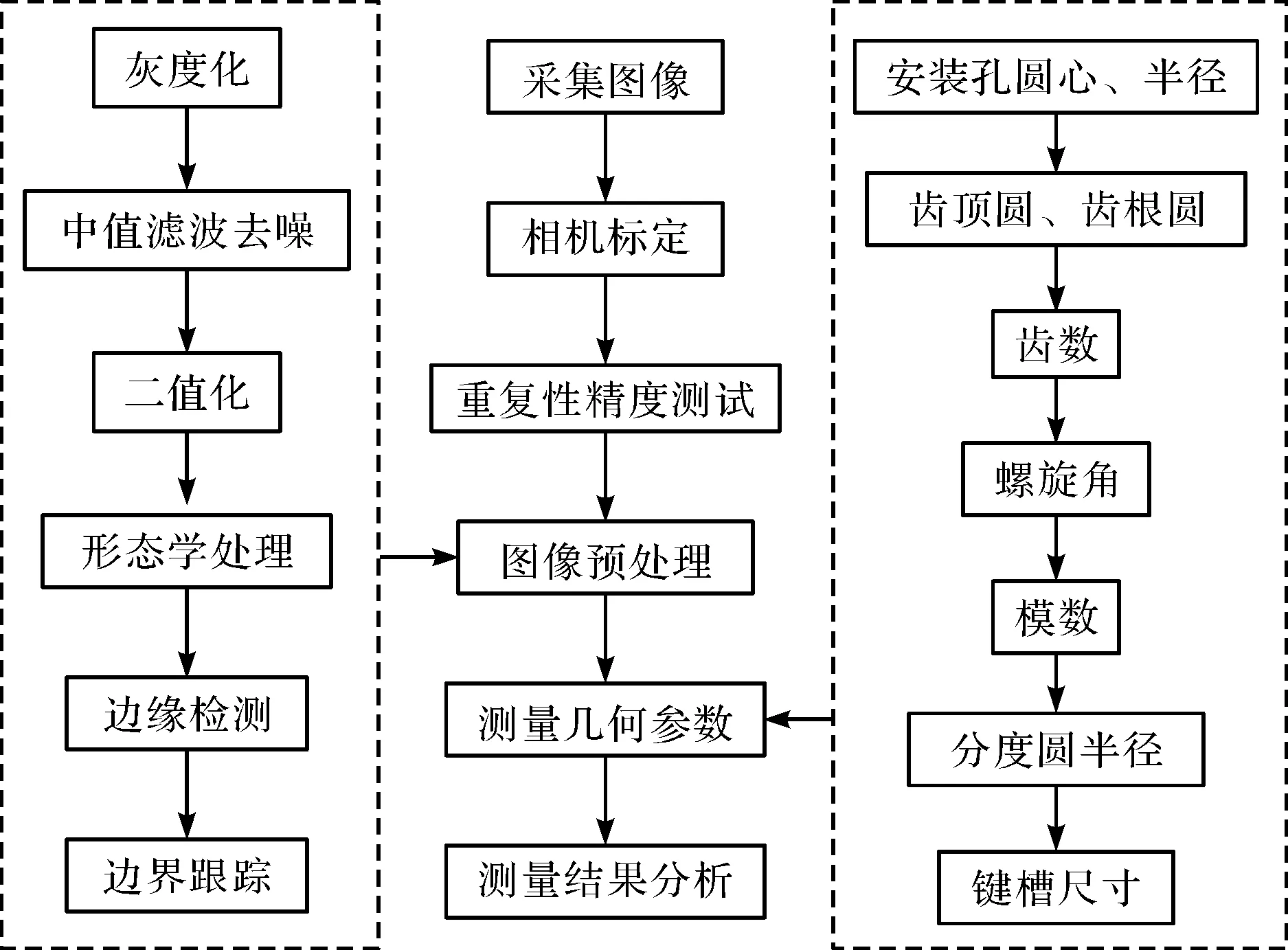
图2 测量流程图

2 相机标定

由于典型FA镜头存在0.5%～1%的畸变率,畸变会影响图像质量,导致图像出现失真,进而会影响测量精度,笔者采用方格边长为5 mm,外形尺寸为70×70 mm的棋盘格标定板,来得到相机的参数属性,进而对图像畸变进行校正。

首先,笔者利用相机拍摄20张标定板图像(每一张标定板位姿都不同),利用MATLAB中camera calibrator工具箱,来对标定板图像进行检测,并得到相机的参数属性,再调用undistortImage函数,即可完成对齿轮图像的畸变校正。

标定板实物图与角点检测图像如图3所示。

图3 标定板实物图与角点检测图像

完成畸变校正后,还需要标定出像素距离与实际距离之间的对应关系[11]。笔者采用公称长度为L,宽度与斜齿轮齿宽一致的标准量块,对相机进行标定。

测量螺旋角时,笔者通过量块组合,选择与齿轮齿顶圆直径相同的量块组。采集完斜齿轮图像后,在保证相机高度与拍摄角度不变情况下,笔者将量块装夹在相同位置,保证量块的成像平面与齿轮成像平面的一致性,进而采集量块图像。笔者再通过对量块图像进行处理,测出量块L的边长所占像素个数为N,最终得到相机像素与公称长度之间的关系K:

(1)

式中:L—量块公称长度;N—量块像素个数。

利用量块标定像素当量K为0.079 1 mm/Pixel,而棋盘格标定板标定像素当量K为0.080 6 mm/Pixel,两者相差不大。

量块原图像与边缘检测图像如图4所示。

图4 标定量块原图像与边缘检测图像

3 重复性精度测试

为了验证系统测量结果的重复性,笔者采用高精度圆形标定板进行重复性精度测试[12]。

此处,标定板圆形阵列4个顶点和1个中心点的中心坐标需要各测量10次,再利用贝塞尔公式计算各个中心点坐标值的标准差σi和不确定度ΔXi。

第i个点第j次测量中心距lij为:

(2)

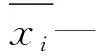
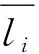
(3)

各个中心点坐标值的标准差σi和不确定度ΔXi为:

(4)

(5)

式中:σi—第i个点测量n次的标准差;ΔXi—第i个点测量n次的不确定度;tα(n-1)—自由度n-1显著水平α下的t分布置信因子。

4 图像预处理

4.1 灰度变换与图像去噪

由于相机采集到的斜齿轮图像中含有夹具干扰,笔者采用k均值聚类分割算法提取齿轮的RGB图像。又由于RGB图像含有大量信息,所占空间大,计算机处理的时间长。因此,需要将RGB图像转化为灰度图,将单个像素由24位降为8位表示,以减少数据量,提高运算速度。

在图像采集的过程中,由于环境光以及设备等因素的影响,不可避免地会产生一些噪声点,噪声点会增加运算量,而且还会影响测量精度,需将噪声点滤除。

此处采用中值滤波来滤除噪声。中值滤波是一种非线性的滤波技术,它在去除噪声的同时,还能很好地保护图像边缘信息,因而是一种常用的去噪手段[13]。

笔者调用MATLAB中Rgb2gray函数,将斜齿轮图像转化为灰度图,调用MATLAB中Medfilt2函数,对图像进行中值滤波去噪。

灰度图与中值滤波图像如图5所示。

图5 灰度图与中值滤波图像

4.2 二值化与形态学处理

二值化是将图像转化为只有0(黑色)和1(白色)两种像素值,整个图像只有黑和白两种颜色,从而突出目标部分,增强图像与背景的对比度,降低图像的信息量。

笔者选择某一阈值T,将图像灰度值大于T的像素赋值为1(目标部分),将图像灰度值小于T的像素赋值为0(背景部分),然后输出二值图像g(x,y)。其公式可表示为:

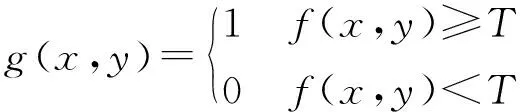
(6)

式中:f(x,y)—灰度图像中(x,y)点的灰度值。

二值化的关键是阈值的选择。笔者采用Otsu算法对阈值进行选取,通过调用MATLAB中graythresh函数选择合适的阈值,再调用im2bw函数对图像进行二值化处理。

由于二值化图像中存在细小的孔洞,这些孔洞会影响后续图像处理以及测量的精度,必须将这些孔洞进行填充。图像的闭运算可以填充图像物体存在的细小孔洞、连接断开部分。

笔者在MATLAB中调用imclose函数对图像进行闭运算处理。二值化和闭运算的结果如图6所示。

图6 斜齿轮二值化与闭运算图像

4.3 边缘检测

边缘检测[14]可以得到斜齿轮的边缘图像,减少后续处理的数据量。经过二值化处理后整幅图像信息进一步简化,齿轮与背景之间的对比度更加明显,突出了齿轮部分,使得边缘检测能够更加清晰、准确地提取齿轮边缘图像。常用的边缘检测算子主要有Canny算子、Prewitt算子、Sobel算子等。通过比较,笔者采用Canny算子。

4.4 边界跟踪

笔者通过边界跟踪函数获得斜齿轮轮廓非零像素点坐标，在齿轮边缘、中心孔上分别选取一点作为起始点,按照8邻域顺时针方向开始搜索,直到边缘搜索完毕后终止。笔者在MATLAB中调用bwtraceboundary函数对图像进行边界跟踪处理。

5 实验及结果分析

由于工作台大小及镜头视野尺寸的限制,可测量的齿轮齿顶圆直径最大值为70 mm,最小值为10 mm。

为了验证上述方法的准确性,笔者选择2个齿顶圆直径分别为66.78 mm、39.62 mm的斜齿圆柱齿轮。其中,齿轮1和齿轮2边界跟踪图像如图7所示。

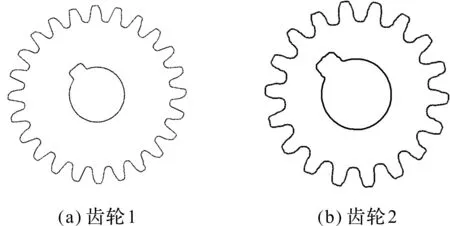
图7 齿轮1和齿轮2边界跟踪图像

具体的测量步骤如下:

(1)重复性精度测量结果。取式(5)中α为0.05,查表得tα(n-1)=2.23,可得到重复性精度测量结果,如表1所示。

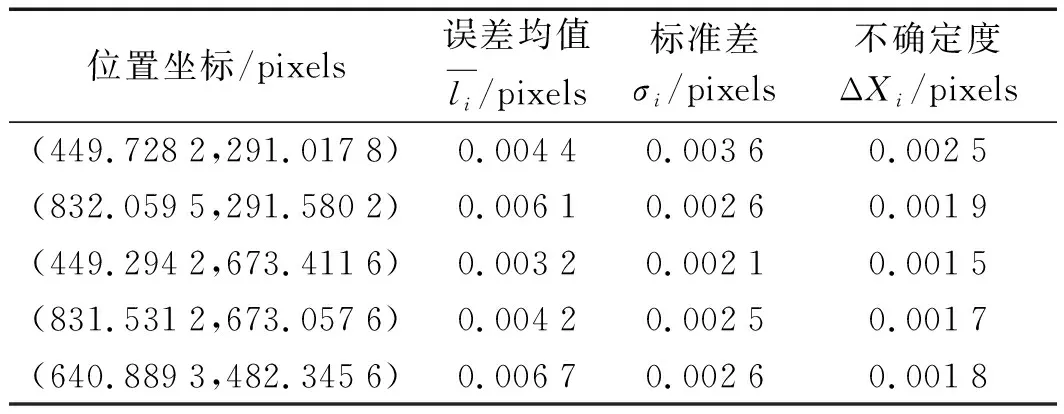
表1 重复性精度测量结果

(2)齿轮中心点。齿轮中心点是测量其他几何参数的基准,齿轮中心点像素坐标可以采用重心法和最小二乘法进行测量[15]。由于中心孔存在键槽,笔者选择最小二乘法进行测量,即提取中心孔圆弧部分的坐标,利用最小二乘法拟合轮廓曲线,从而得到中心点像素坐标以及中心孔半径值。

(3)齿顶圆、齿根圆半径。采用的算法如下:计算每个齿廓边缘点到中心点的距离值,统计在这些距离值区间内像素点距离值的分布情况。

齿廓像素点到中心点像素距离的分布情况,如图8所示(横坐标为齿廓像素点到中心点的像素距离值,纵坐标为齿廓像素点到中心点像素距离分布在各个区间内的个数;A、B两点横坐标分别对应齿根圆、齿顶圆半径信息)。

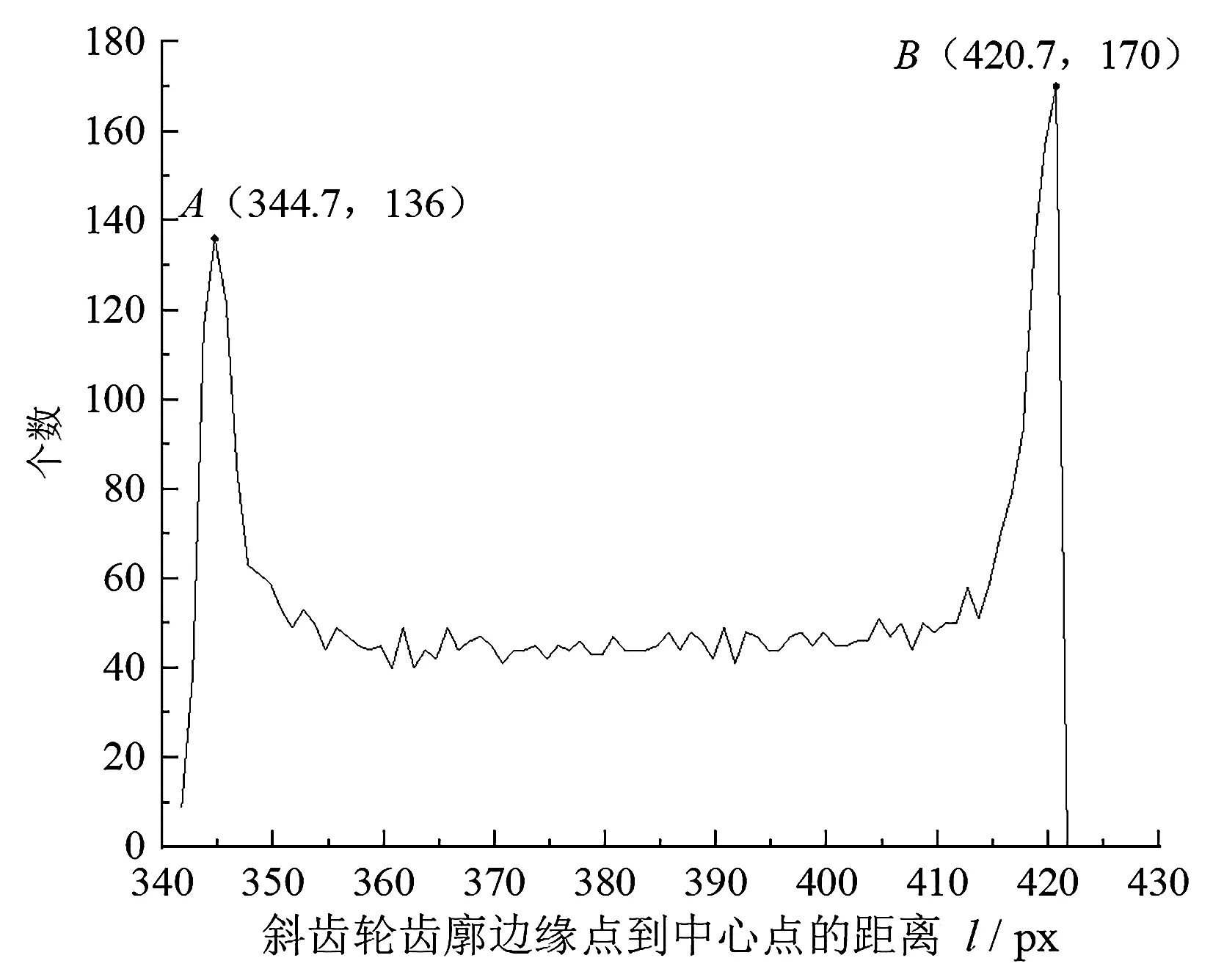
图8 齿廓像素点到中心点像素距离的分布图

在加工过程中,由于存在着齿坯安装孔轴线和机床工作台心轴轴线不重合引起的几何偏心,部分实际齿根圆、齿顶圆半径值与设计值之间会存在误差。因此,在计算得到所有距离值后,笔者在最小值到最大值的区间内,每隔1 Pixels划分为一个小区间,统计这些距离值落在各个小区间内的个数,数目最多的两个区间对应的两个距离值分别对应齿根圆、齿顶圆半径信息。

(4)齿数测量。需要用到步骤(3)中测量的齿廓边缘点到中心点的像素距离。理想状态下,齿廓边缘点到中心点的距离分布曲线应是周期变化的。

齿廓边缘点到中心点的像素距离分布曲线图及曲线局部放大图如图9所示。

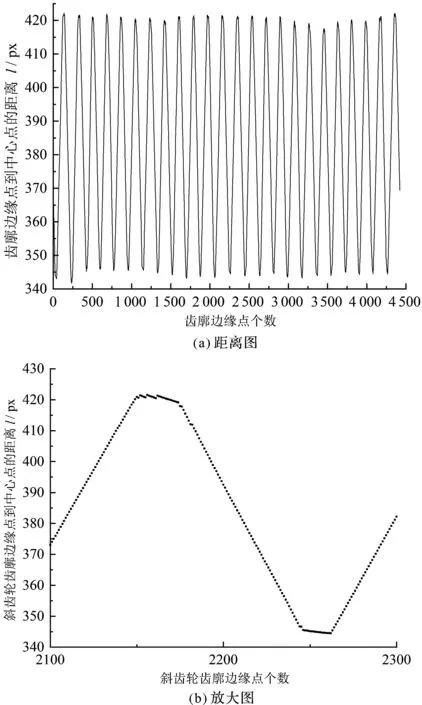
图9 齿廓边缘点到中心点的距离及放大图

图9(a)中:纵坐标为齿廓边缘点到中心点的像素距离,横坐标为齿廓曲线上像素点个数的序列(该序列从1到4 422,其从边界跟踪起始像素点,按顺时针方向依次排列齿廓曲线上的全部像素点)。

图9(b)中:周期分布曲线的顶部像素点的个数,即为一个轮齿齿顶圆弧部分像素点的个数;同理,曲线底部像素点的个数即为一个轮齿齿根圆弧部分像素点的个数。

由于存在加工误差,每个齿廓部位的齿顶圆、齿根圆半径值存在一定的波动。笔者设置一个距离变化区间,该区间为齿根圆半径加10到齿顶圆半径减10;通过设计算法,计算齿廓边缘点到中心点的像素距离从最小到最大区域的次数,通过统计次数即可测得齿轮的全部齿数。

(5)斜齿轮螺旋角。斜齿轮螺旋角部分实物及检测图,如图10所示。

图10 斜齿轮螺旋角部分实物及检测图

槽型柔性组合夹具加工有T形槽,利用定位块可将斜齿轮装夹固定在T形槽内,经过多次调整夹具中定位键的位置来保证齿轮端面与工作台平面垂直。通过步进电机可以驱动工作台转动,经过细分驱动器细分后步距角可达到0.12°。经过多次调整工作台旋转角度,参考相机视野水平线,保证齿轮端面和视野水平线垂直。水平方向偏差为细分后步距角0.12°。

笔者对螺旋角[16]实物图像进行预处理,利用Hough变换得到检测图像(Hough变换是一种常用的直线检测方法,它将图像上的一个点转换为参数空间的一条曲线[17]),图像上共线的点对应参数空间的曲线会相交于一点,可通过统计累加器中的极大值来对直线信息进行提取。提取直线信息后可得到直线的两端点坐标值,从而计算出斜齿直线的斜率k1,水平直线的斜率k2为0。

通过两直线夹角公式可以求得斜齿轮螺旋角β:

(7)

式中:k1—斜齿直线斜率;k2—水平直线斜率。

(6)模数通过间接测量得到。根据齿顶圆半径da、模数m、齿数z与螺旋角β之间的关系,可经过计算得到,即:

(8)

式中:da—斜齿轮齿顶圆直径;z—齿数;β—螺旋角。

先利用公式(8)计算出一个模数值,再将其与国标中标准模数值进行比较,最终得到实际模数值m。

(7)分度圆直径d通过间接计算得到。可通过齿数z、模数m和螺旋角β的关系得到,即:

(9)

式中:z—齿数;m—模数;β—斜齿轮螺旋角。

(8)齿轮键槽参数。齿轮键槽图如图11所示。

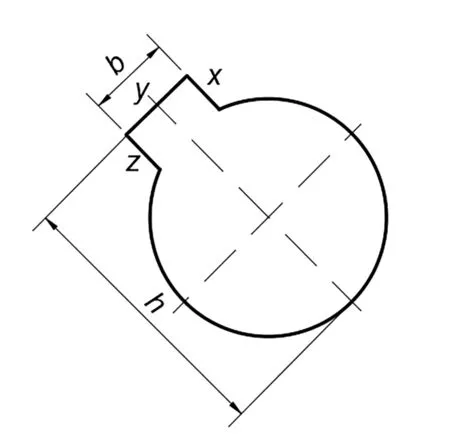
图11 键槽图

笔者利用最小二乘法拟合出键槽的3条边缘直线x,y,z,求得两交点的距离即为键槽宽度值b,齿轮中心点到键槽底面直线y的距离值加中心孔半径值,即为键槽深度值h。

(9)笔者采用人工和本文方法分别测量两个齿轮的几何参数,各10次,求其平均值,得到人工测量值和图像测量值,最后将测量结果进行对比分析。

其中,齿轮1人工测量与图像测量结果对比如表2所示。

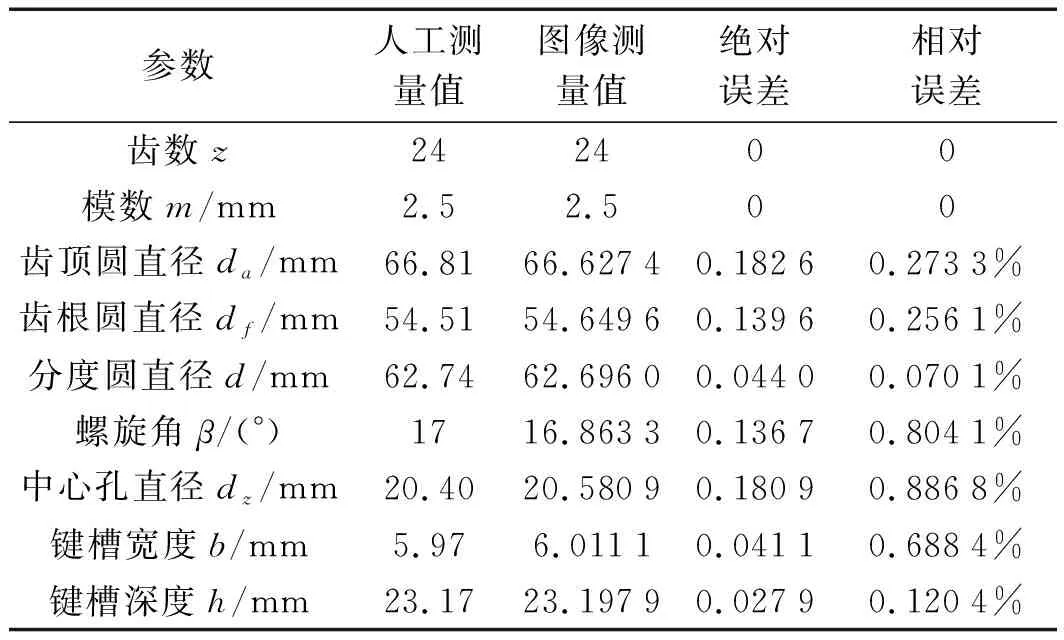
表2 齿轮1人工测量与图像测量结果对比

齿轮2人工测量与图像测量结果对比如表3所示。

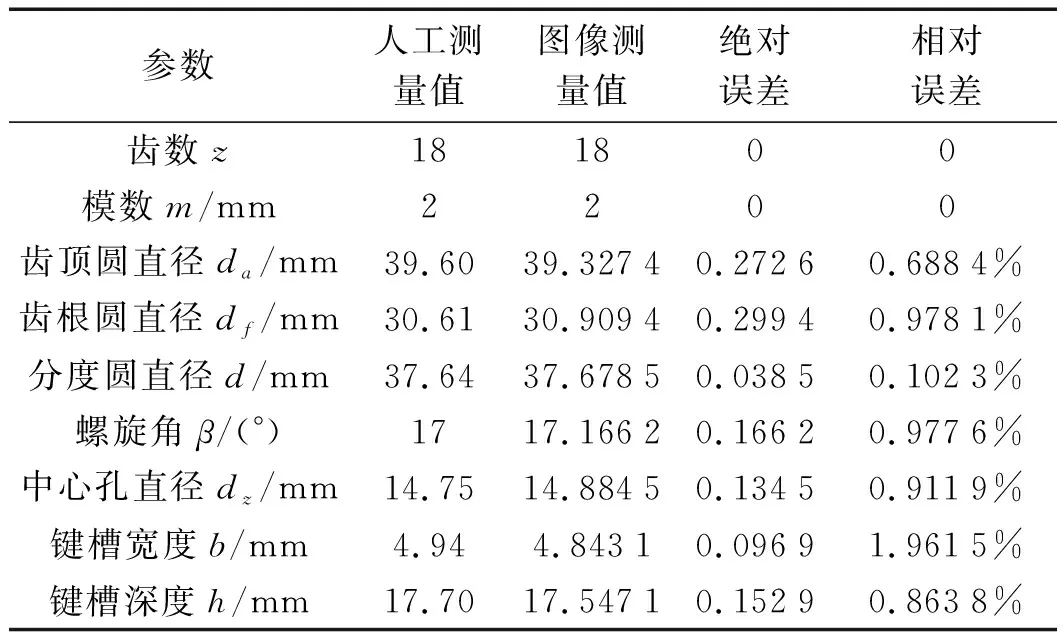
表3 齿轮2人工测量与图像测量结果对比

从表2和表3可以看出:

(1)齿轮1、齿轮2的齿数z和模数m测量结果不存在误差,齿轮1其他参数相对误差均在1%之内,齿轮2其他参数相对误差均在2%之内;(2)由于在相同拍摄条件下齿轮1的尺寸大、齿数多,边缘检测精度较高,尺寸大的齿轮1测量精度较高。

6 结束语

笔者提出了一种基于视觉原理的斜齿轮几何参数测量方法。首先，用MATLAB软件对图像进行了一系列预处理操作;然后,设计了相关的算法,以自动、准确地测量出齿数、模数、齿顶圆直径、齿根圆直径、分度圆直径、螺旋角、中心孔直径、键槽宽度和深度等参数;最后对测量系统进行了重复性精度测试。

研究结果表明:

(1)与人工测量结果相比,大、小齿轮各项参数相对误差分别不超过1%和2%,满足自动、准确测量斜齿轮几何参数的要求;

(2)测量系统不确定度均小于0.003 pixels,表明系统的测量结果比较稳定、可靠;

(3)由于在相同拍摄条件下大齿轮的尺寸大、齿数多,边缘检测精度较高,针对大齿轮的测量精度较高。

由于当前的算法只考虑了图像像素级边缘检测和齿轮几何参数的测量,在接下来的研究中,笔者将对图像亚像素级边缘检测和齿轮齿距偏差、齿廓偏差测量进行深入研究,以不断提高、完善该方法的测量精度及通用性。