基于数值模拟的水下节流阀早期冲蚀故障特征分析*

2021-11-27 04:35王泓晖田晓洁刘贵杰

机电工程 2021年11期

关键词：节流阀冲蚀增量

房鑫,王泓晖,田晓洁,刘贵杰

(中国海洋大学机电工程系,山东青岛 266100)

0 引言

随着陆地油气资源的逐步枯竭,储量多且潜力大的深海油气资源现已成为能源供给的重要途径。

现阶段,水下生产系统是实施深海油气资源开发和利用的首选方式[1]。但由于深海油气生产是在高温、高压的恶劣条件进行的,对水下生产系统的安全、可靠运行带来了极大挑战[2]。

水下节流阀是水下生产系统的核心部件[3],它在深海油气生产中,起到控制油气启动、停止和调节生产的关键作用。同时,由于该部件直接面对高温、高压、高速,且携带砂砾的油气资源,使其成为出现失效和故障的重灾区。

相关调研资料表明,较其他水下阀门,水下节流阀失效概率更高,约是水下闸阀的6倍[4];而且在某些极端情况下,水下节流阀阀芯可能会在10 h～12 h内受到砂砾的冲蚀而出现节流失效现象[5],引发停产等事故的发生。为此,对水下节流阀的故障诊断进行研究,对保证深海油气资源的安全生产具有重要意义和价值。

阀芯的冲蚀故障是水下节流阀的主要故障类型之一,约占其各种失效类型的28%。现阶段,围绕着阀芯的冲蚀故障,国内外学者已经展开了很多的研究工作。例如,MALAVASI S等人[6]、PAGGIARO R等人[7]和战晓溪等人[8]基于计算流体力学方法,探索了阀芯在工作时的主要失效模式和机理,重点分析了油气流动参数对冲蚀的影响规律,提出了阀芯和阀套的冲蚀故障诊断模型,取到了较好的诊断效果。除此之外,HAUGEN K等人[9]建立了阀芯的性能退化经验公式,并据此分析了阀芯的冲蚀故障,证明该经验公式具有一定的工程实际应用价值。

然而,上述研究主要是针对陆基节流阀展开的研究,尚未涉及到水下节流阀。虽然二者的研究方法可以借鉴,但因为水下节流阀阀芯冲蚀程度一旦超过其阈值,将会导致水下生产系统停产,造成极大的经济损失。同时,当前的研究常使用阀门值进行阀芯冲蚀磨损诊断[10],该方法虽然具有一定的有效性,但是难以在冲蚀损伤初期对其进行故障的有效识别。为此,有必要探求得到能够有效表征阀芯早期冲蚀退化的特征量,以便据此安排维护、维修计划,将损失降低到最低。

根据以上论述,笔者以笼套式水下节流阀为研究对象,通过对其冲蚀退化过程进行仿真,从时域分析和频域分析两个角度出发,得到能够有效表征其冲蚀故障的特征量,以期为水下节流阀阀芯的早期冲蚀故障诊断提供依据和参考。

1 水下节流阀阀芯冲蚀数值仿真模型

1.1 研究对象

为了研究水下节流阀阀芯的冲蚀故障诊断方法,笔者选取CAMERON公司生产的COMPACT型笼套式水下节流阀作为具体的研究对象。

该节流阀如图1所示。

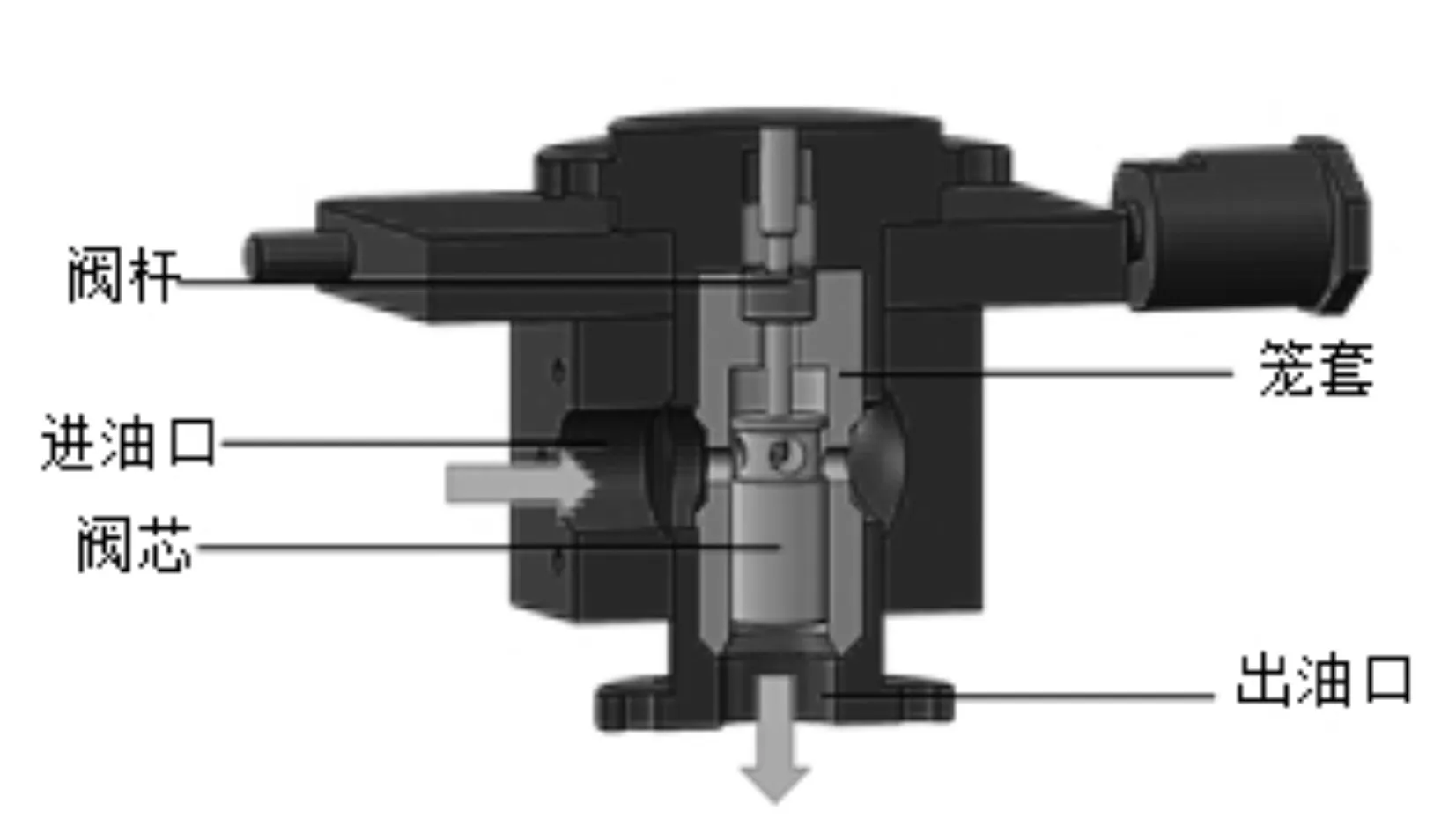
图1 水下节流阀

该水下节流阀由执行结构和阀体两部分构成,其中,阀芯位于阀体中,它由执行机构进行驱动,通过上下移动的运动形式,调节过油孔的流通面积,实现对油气资源进行节流控制。

由于本次研究侧重于阀芯的冲蚀退化过程,探究的着眼点聚焦于阀体部分,笔者仅建立由阀芯、阀座和阀体构成的数值分析模型。

其相关的材料参数如表1所示。

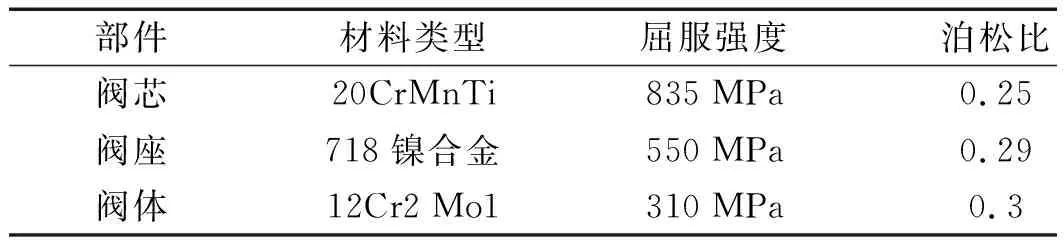
表1 阀芯、阀座和阀体的主要材料属性

1.2 阀芯冲蚀退化仿真分析方法

1.2.1 冲蚀退化模型

由于阀芯的冲蚀退化是由高速流动的油气资源(含砂砾)的冲击造成的,该退化机理可通过Tabak off-Grant模型[11]进行分析。该模型具有计算精度高、适用参数范围广等特点,被广泛用于实际生产中各类冲蚀率的计算。

冲蚀率公式如下:

(1)

其中:

(2)

式中:E—冲蚀率;γ1—砂粒的撞击角度,rad;VP—砂粒的撞击速度,m/s;RT—切向恢复比;γ0—砂粒的最大撞击角度;V1,V2,V3,k2,k12—常数,取值与颗粒性质和靶材材料有关。

由上述公式可知,阀芯冲蚀退化的速率是颗粒形状、颗粒冲击角度、材料类型和冲击速度之间的函数,且该函数关系是连续的。在进行有限元仿真时,还需要将该模型离散化,即认为冲蚀过程是多个冲蚀量的累积,且在足够小的增量步中,模型中各个变量和系数是恒定不变的。

根据有限元理论,冲蚀退化过程可分解到每个节点的冲蚀量上,其具体表达方式如下:

ei,n=ei,n-1+Δer

(3)

式中:ei,n—第i个节点在第n个增量步下的冲蚀总量;ei,n-1—第i个节点在第n-1个增量步下的冲蚀总量;Δer—两个增量步之间的冲蚀量,符合式(1)。

1.2.2 阀芯冲蚀退化的形状特征更新

阀芯产生一定程度的冲蚀退化后,会导致阀芯过油孔处的几何形状发生改变[12],如图2所示。

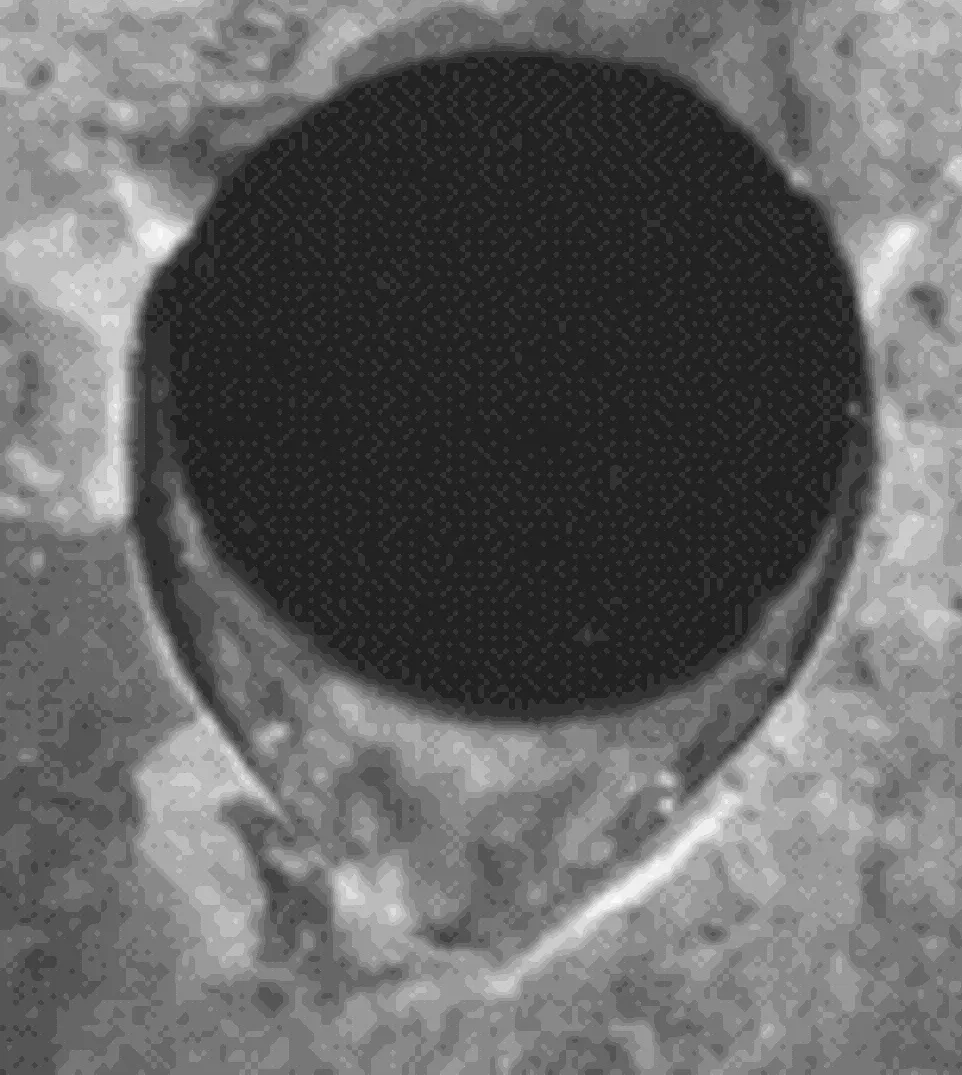
图2 冲蚀损伤

此时有两种更新方式:(1)采用生死单元法,将受损的单元删除或者作无效化处理;(2)采用节点位移技术,通过移动节点的方式,完成其几何形状的更新。

对于上述第一种方法,容易造成单元之间的不连续,进而引起迭代计算过程不收敛,故而此处采用第二种方式。

同时,如果节点位移过大,会出现网格畸变、负体积等问题,直接导致仿真过程失败。为此,笔者引入ALE自适应网格技术,通过网格重画的方式来解决上述问题。

ALE自适应网格技术如图3所示。

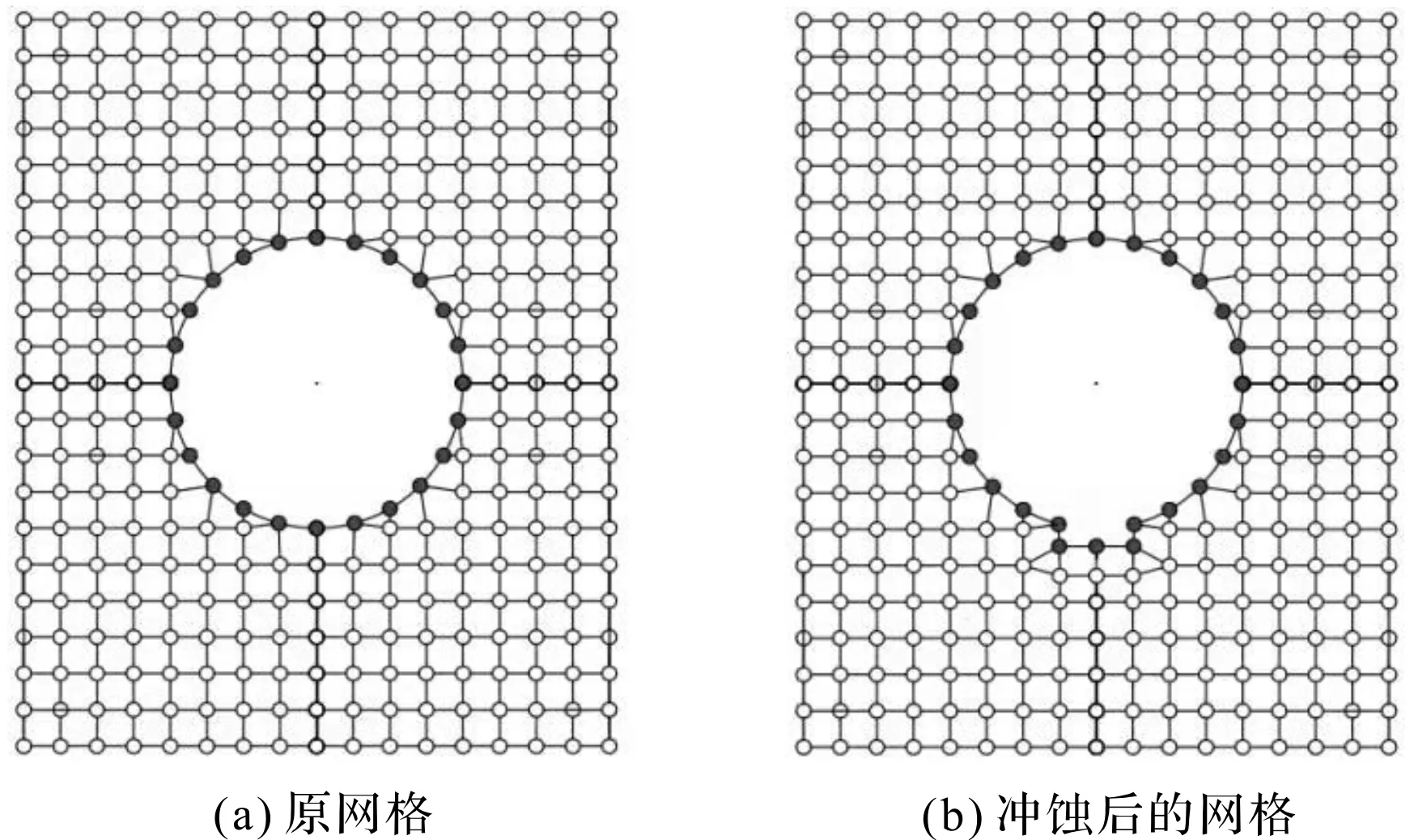
图3 ALE自适应网格技术

1.2.3 油气流动过程仿真

阀芯的冲蚀由油气流动导致,因此还需要对该流动过程进行仿真。该油气资源为地层原油,涵盖元素多且组成复杂,是一种典型的多相流。

原油参数如表2所示。

表2 原油参数

由于对多相流运动的仿真效果好、精度高,近年来,耦合欧拉-拉格朗日方法(coupled Eulerian Lagrangian,CEL)在业界得到了广泛应用。为此,本研究采用该方法来对原油流动过程进行仿真。

其相关仿真流程如图4所示。

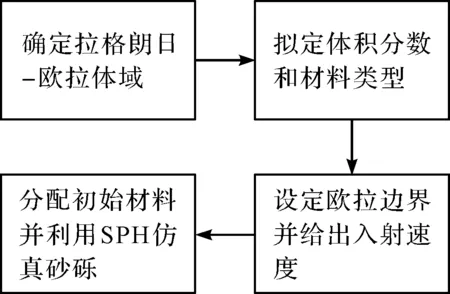
图4 原油多相流CEL仿真步骤

由图4可作如下论述:

(1)建立拉格朗日-欧拉体域(一般为立方体域),确定欧拉体积分数;同时,拟定欧拉单元的材料类型,并令该域包裹整个阀体;

(2)设定欧拉边界,指定入口类型和出口类型(压力边界、自由边界等),给定入射速度;

(3)在入口处分配初始材料,否则无法实现原油的流入;

(4)利用SPH技术仿真砂砾,完成携带砂砾的油气资源流动的模拟过程。

1.2.4 阀芯冲蚀仿真流程

通过在ABAQUS环境中开发UMESH-MOTION子程序,并结合网格自适应技术,同时利用CEL获得的油气资源流动仿真过程,可以完成对阀芯冲蚀的模拟和分析。

具体的流程如图5所示。

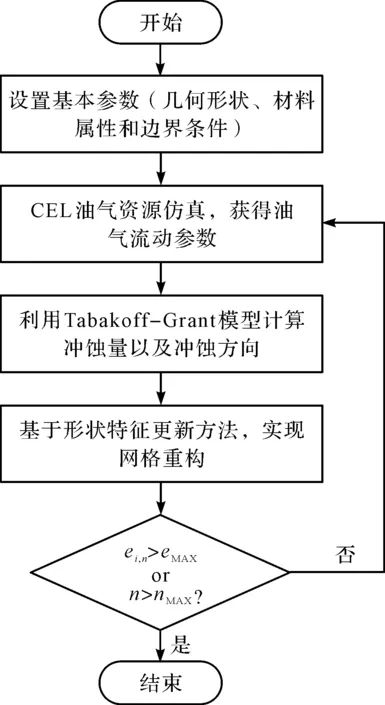
图5 阀芯冲蚀仿真流程

由图5可知:

(1)在UMESH-MOTION程序中,基于CEL求解结果,可以获得颗粒形状、颗粒冲击角度、材料类型和相对冲击速度等参数;

(2)使用Tabak off-Grant模型计算冲蚀量以及冲蚀方向;

(3)在每个增量步中,利用形状特征更新方法来实现几何与网格重构,并存储此时的冲蚀量;

(4)不断重复上述过程,直到增量步达到预定值或者冲蚀量达到预定最大值。

基于以上内容,笔者在ABAQUS中建立起针对阀体且面向阀芯冲蚀过程的有限元仿真模型,如图6所示。

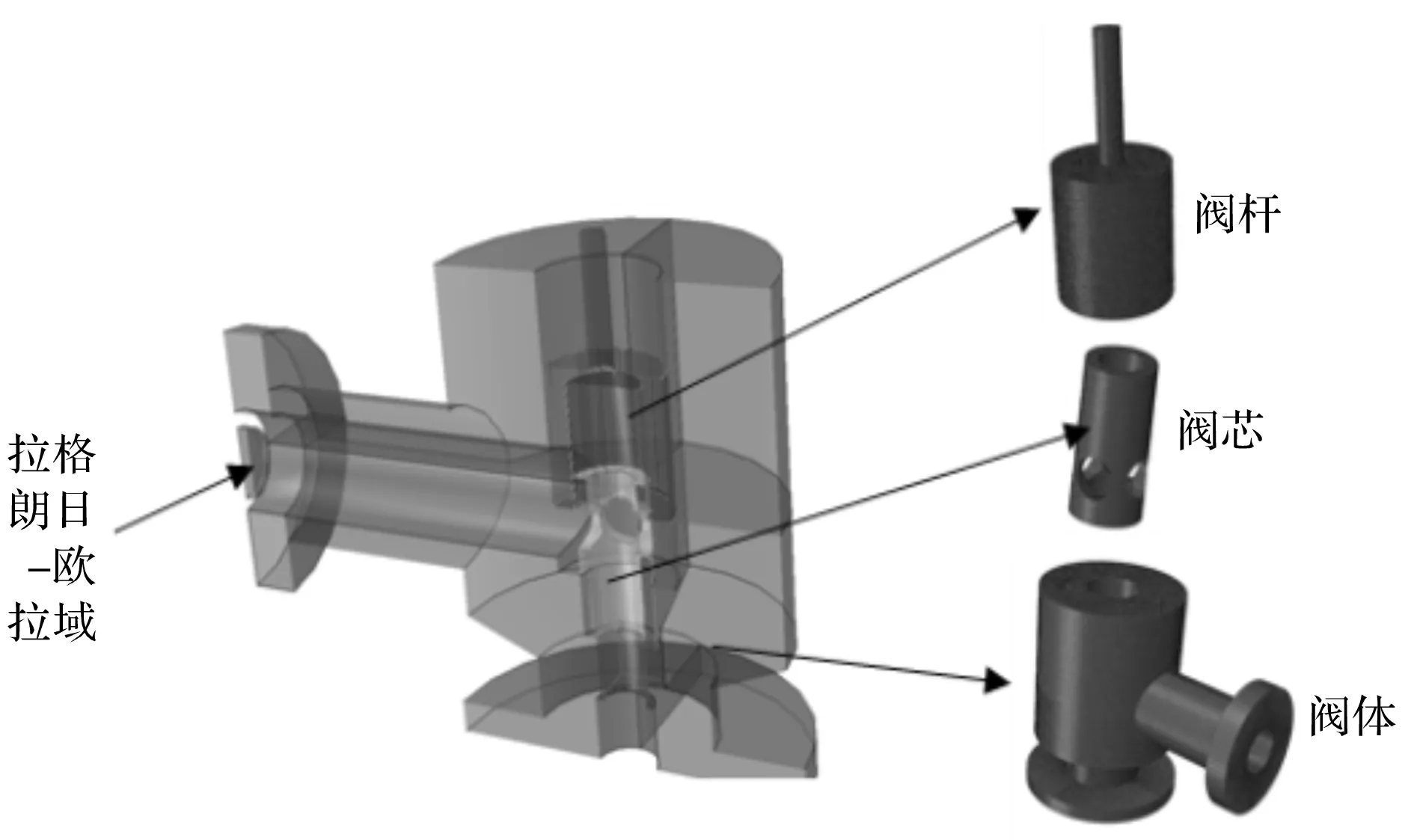
图6 有限元仿真模型(基于ABAQUS)

2 水下节流阀阀芯冲蚀仿真

2.1 仿真工况

由于油气资源流动参数以及阀芯过油孔的流通面积(阀门开度)等工况参数,会直接影响阀芯冲蚀退化的过程和阀芯产生冲蚀故障的时间,笔者将DNV-GL(2015)手册[13]拟定的油气流动工况,作为实施模拟的基本参数。

油气流动工况的参数如表3所示。

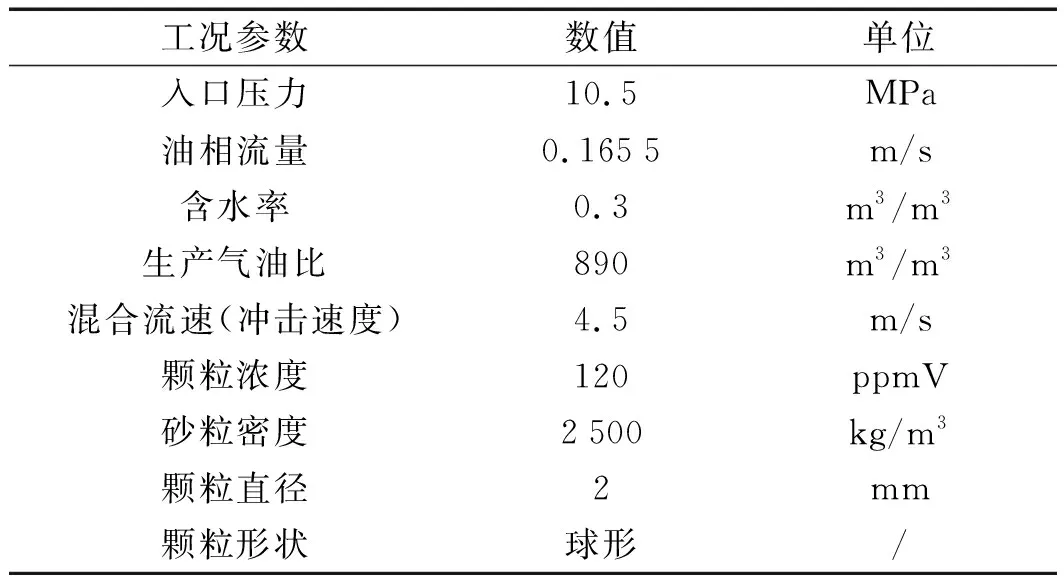
表3 油气流动工况参数

由于颗粒为沙子,阀芯材料为20CrMnTi,笔者依据参考文献[14]的参数选用原则,并结合表3给出的工况数据,来确定出冲蚀率计算公式中的各个常数。冲蚀计算公式常数的确定如表4所示。

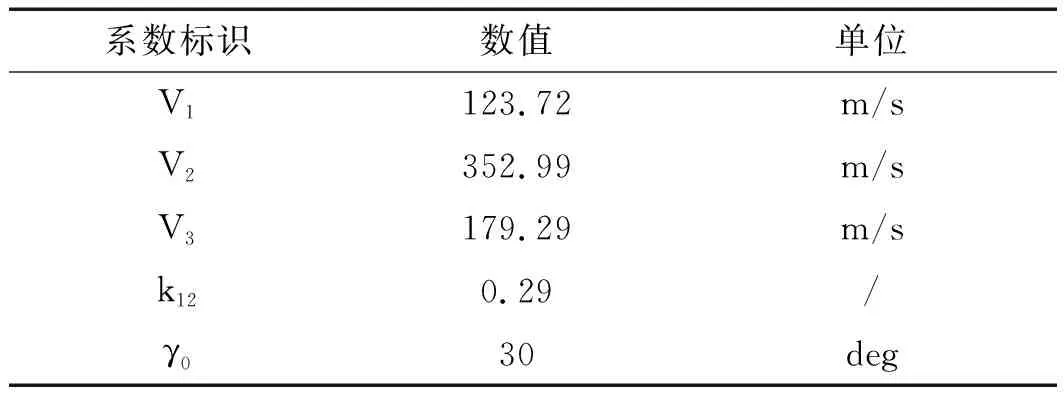
表4 冲蚀计算公式常数确定

笔者将阀门开度调至100%,在表3中所述的工况作用下,通过仿真分析水下节流阀的冲蚀故障,将冲蚀部分近似表示为圆形,采用冲蚀圆半径与过油孔半径的比值,作为冲蚀退化程度的描述值。

2.2 故障特征信息提取及仿真测点布置

在ABAQUS环境中,利用构建的有限元模型,可以获得阀门在工作时的各种力学和运动学数据,例如,流场内某处的压强和流速、阀门外部某处的振动特征等。而随着冲蚀退化程度的逐步加大,这些数据均会较之前未发生冲蚀时发生一定程度改变,从而反映出当前的冲蚀故障。

为此,本文通过数值模拟的方式,提取阀门运行过程中的振动特征和流场特征,作为故障特征信息,来分析阀芯的冲蚀故障。

为了获得上述特征,需要给出仿真环境下的测点布置方式(简称仿真测点)。其具体布置原则为:(1)面向流场特征提取的仿真测点,主要集中在阀门出口处,采取定深环状布置的形式,以尽可能获得流场相对全面的压强和流速数据;(2)面向振动特征提取的仿真测点,安置在靠近阀芯的阀门外侧,以捕捉由阀芯冲蚀故障引起的特征信号。

仿真测点的具体布置方式如图7所示。

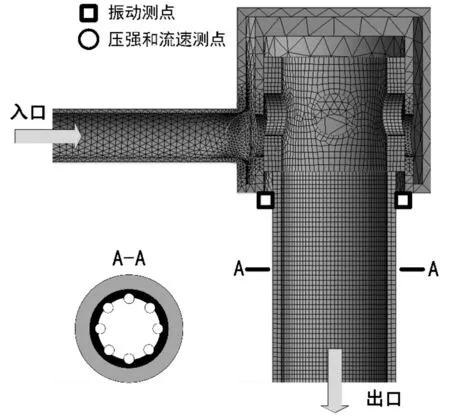
图7 仿真测点布置

2.3 仿真流程

阀芯冲蚀数值仿真的试验流程如下:

(1)基于给定的油气流动工况参数,将阀门开度调至100%,进行阀芯冲蚀退化仿真,验证构建有限元仿真模型的有效性;

(2)将阀门开度调至最大,存储各个仿真测点的数据;

(3)提取仿真测点特征值,分析在相应冲蚀量下的特征值变化情况,并按照敏感性对特征值进行筛选,以构建起与早期冲蚀故障之间的联系。

3 仿真及结果分析

3.1 冲蚀有限元仿真模型有效性验证

笔者在某工作站完成该仿真试验。该工作站CPU配置为Intel Xeon-W3175X,内存为128 GB,可满足上述内容的数值模拟要求。在仿真时,笔者设定了104个增量步,用于模拟节流阀阀芯的冲蚀退化过程。

计算前和计算后的阀芯形状特征如图8所示。

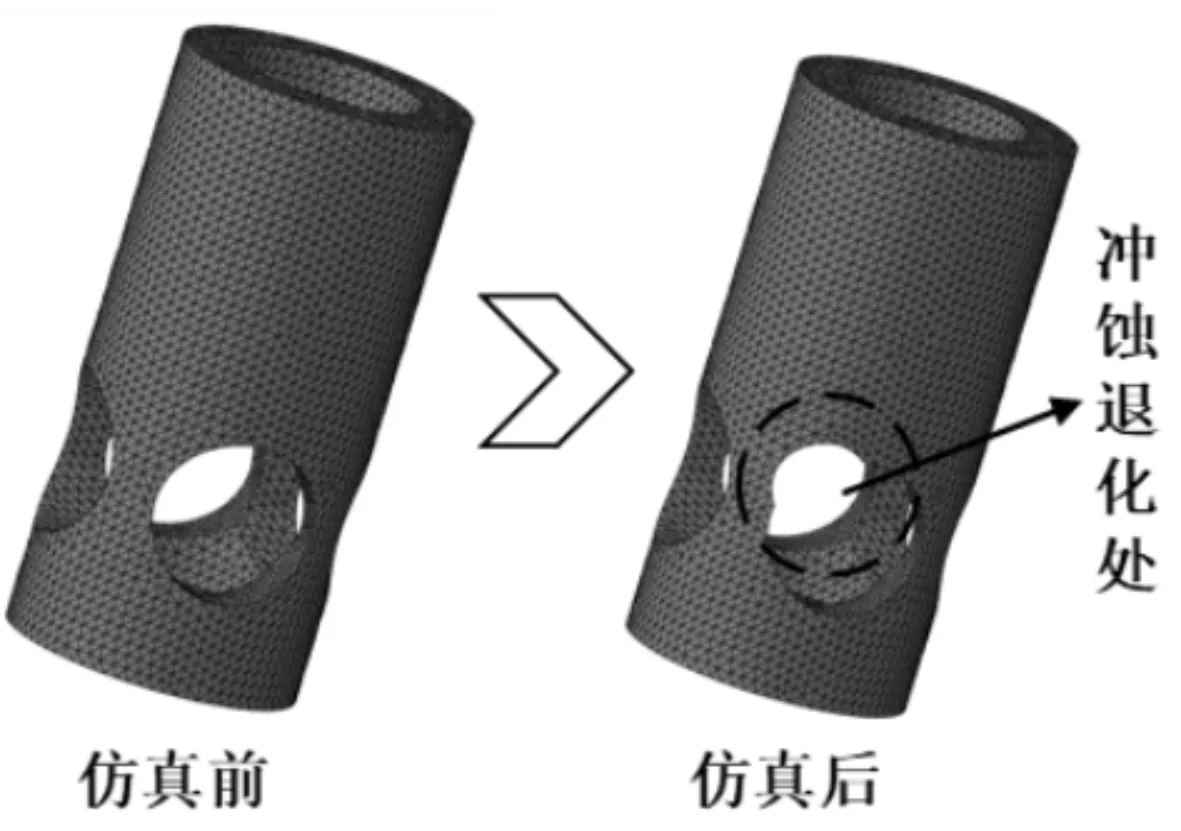
图8 阀芯形状特征变化

由图8可知:经过冲蚀模拟后,阀芯出现了较为明显的冲蚀退化现象。

在实际生产中,常用节流阀整体质量损失来表征其冲蚀状态,拟定一个总的质量损失作为阀门的失效标准。该标准需根据阀门的结构和材料性能,经泥浆实验得出。

根据该方法,此时的质量损失为2.24 kg,而失效标准为7.2 kg,冲蚀退化程度约为32%。但该方法需将阀门由井口设备拆下,并提升至水面进行测量,这个过程存在风险,并造成经济损失;同时,该方法也无法对阀门的冲蚀退化程度进行实时监测。

为解决以上的实时监测问题,有学者提出利用阀门流量系数(Cv)的值,来判断是否达到了阀芯的使用寿命[15]。

相关资料显示:当流量系数增量ΔCv大约为7时(阀门全开时),阀芯被认为失效。

Cv的计算方法如下:

(4)

式中:qv—体积流量;ρ—流体密度;Δp—阀门压力损失。

笔者利用式(4),计算得到阀门未发生冲蚀损伤和冲蚀损伤退化程度为32%时的Cv值,分别为21.68和29.23,增量为7.55,此时可认为阀门已经发生了较为严重的冲蚀故障,达到了其更换阈值。

通过以上仿真结果和分析可知:笔者构建的有限元模型可以对阀芯的冲蚀退化过程及冲蚀故障进行仿真,且在给定工况下的104个增量步内,包含其从未冲蚀损伤到冲蚀失效的整个过程。

3.2 冲蚀程度变化及仿真测点特征值分析

在给定工况下,冲蚀程度与增量步之间的映射关系如图9所示。

图9 冲蚀程度变化曲线

由图9可知:冲蚀程度前期变化较缓,后期变化较快,符合冲蚀退化过程的基本规律。阀门冲蚀退化故障诊断的关键是通过对仿真测点的分析,得到能够表征早期冲蚀退化的特征量。

为了能够方便论述,此处列出了流场测点位置的标识,如图10所示。

图10 流场测点位置标识

随着仿真过程的进行,流场测点压强和流速也发生相应的改变,其压强变化曲线如图11所示。

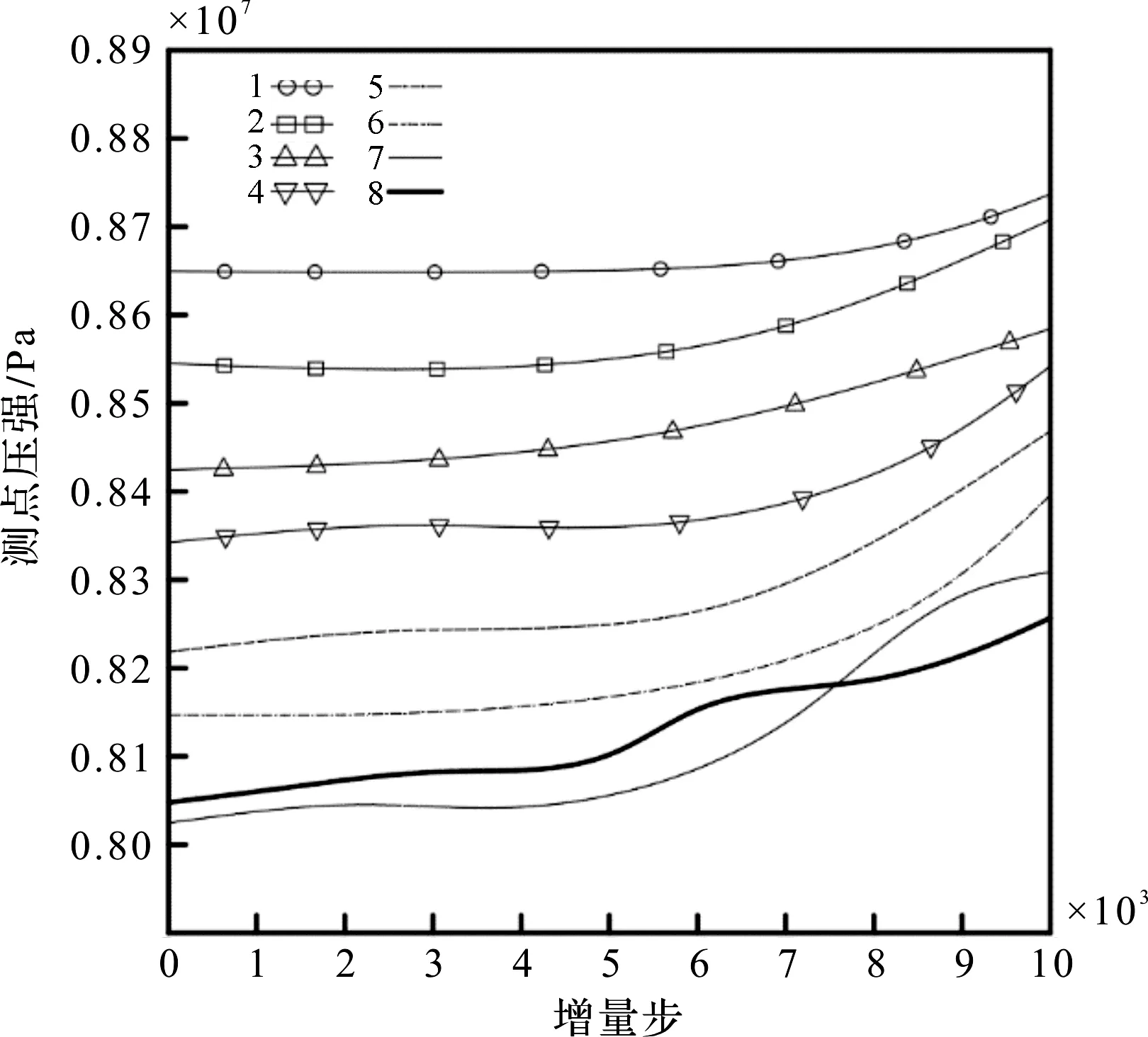
图11 压强变化曲线

流速变化曲线如图12所示。

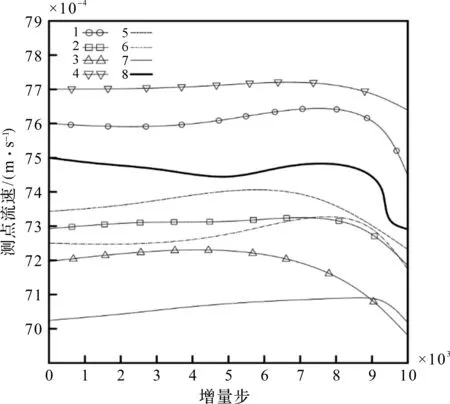
图12 流速变化曲线

通过分析图11、图12的曲线可以发现:

(1)无论是测点的压强还是流速,在6×103个增量步之前,均没有出现较大的变化幅度,而此时冲蚀程度在7%左右,已经出现一定程度的冲蚀损伤;(2)曲线只有在9×103个增量步之后,才出现较为明显的变化,这时的冲蚀程度已经在20%左右,损伤程度已较为严重。

简而言之,仅通过此种类型曲线还不能诊断阀芯早期的冲蚀退化故障,还需进一步提取数据特征。

虽然测点的压强和流速对早期冲蚀退化敏感性较低,但是分析图11和图12也可发现,在冲蚀退化的后期,8号测点的速度变化幅度较大,这是因为该测点距离阀芯冲蚀退化的位置相对较近,敏感性较高。

实际上,上述分析主要侧重时域分析策略,此种策略虽然能够有效表示某个参量随时间变化的规律,但是分析过程较为复杂,难以提取到其细微的变化特征。频域分析法可有效弥补上述不足。频域分析法通过获取诸如固有频率和功率谱密度等特征值,表征其与故障程度之间的关系。由已有的文献资料可知,功率谱密度是一种可有效表征系统故障的特征量[16]。

为此本研究针对该仿真测点的速度变化曲线,采取频域分析法来计算速度的功率谱密度值,该值可以识别出各频率成分功率能量的分布关系,可以很好地提取到故障特征量。针对整个仿真过程,每隔500个增量步,笔者计算一次功率谱密度值。

4 结束语

笔者以笼套式水下节流阀为研究对象,基于数值仿真的方式,构建了水下节流阀阀芯冲蚀退化的有限元分析模型,得到了能够有效表征其冲蚀故障的特征量,并在给定工况下,对该阀芯冲蚀故障进行了模拟,得到以下结论:

(1)笔者使用冲蚀退化模型、CEL仿真方法和UMESHMOTION程序接口构建的冲蚀模型,可以完成对节流阀整个服役期冲蚀退化过程的模拟仿真;

(2)笔者使用监测测点(振动数据和流速数据)的功率谱密度值作为特征量,可大概率诊断出冲蚀程度在10%的冲蚀故障。

在之后的研究中,笔者拟进一步探索功率谱密度值以外的特征量(如裕度、峭度等)对水下节流阀阀芯冲蚀退化过程的敏感性,以进一步提高冲蚀故障识别的程度;同时,将展开水下节流阀阀芯的冲蚀退化实验,分析并验证相应特征量在实际工况下的有效性。