基于改进NSGA-II的多无人机三维空间协同航迹规划研究
王 猛,王道波,王博航,周晨昶,姜 燕
(南京航空航天大学自动化学院,江苏 南京 210016)
0 引言
现如今,无人机自主能力不断完善,环境感知和认识能力愈发成熟,在越来越多的领域大显身手;另一方面,飞行任务多样性和复杂性不断上升,促使无人机集群自主控制成为了新的研究热点[1]。
其中,协同航迹规划为多无人机提供执行任务的最优航迹,是保证任务完成的重要环节[2]。目前,大部分算法[3-4]存在将多个目标条件人为加权求和,变为单一目标进行讨论的情况,结果受加权系数影响较大。Deb等[5]在2001年提出了多目标优化算法——非支配排序遗传算法(non-dominated sorting genetic algorithm II,NSGA-II),该算法使用Pareto最优解集,避免了多目标单一化处理,正广泛应用于多个领域[6-7];Lee等[8]将纳什均衡方法与NSGA-II算法相结合,在仅考虑空间协同约束的条件下,有效解决了多无人机航迹规划问题;周德云等[9]将时间协同和空间协同作为约束条件,在包含威胁区的二维平面内规划出多无人机航迹,但忽略了拥挤度算子,降低了种群个体的多样性,易陷入局部最优。
目前,针对多无人机协同航迹规划,依旧存在以下问题:
a.部分算法在二维平面内进行讨论。
b.缺乏同时考虑无人机的机动性能约束和协同约束,或约束条件描述不够详细。
c.使用算法缺少寻优能力和收敛性上的改进。
本文使用改进后的NSGA-II算法,在三维空间中进行多无人机协同航迹规划。首先,构建多无人机飞行环境的数学模型,选用双染色体编码方式表示无人机航迹;同时考虑自身性能约束和协同约束,并对算法进行改进:优化交叉和变异概率,在选择操作和精英保留策略中引入时间空间协同系数的比较;最后,进行仿真实验,与改进前的NSGA-II算法进行对比,证明改进后算法的优越性。
1 问题描述
假设在某片区域中,地势和地形已通过卫星等方式获取,区域内包含敌方雷达,如图1所示。同时,任务区域内存在许多控制点,位置已知,且部分控制点也处于雷达的检测范围之内。为控制此片区域,无人机必须要反复检查控制点处情况。
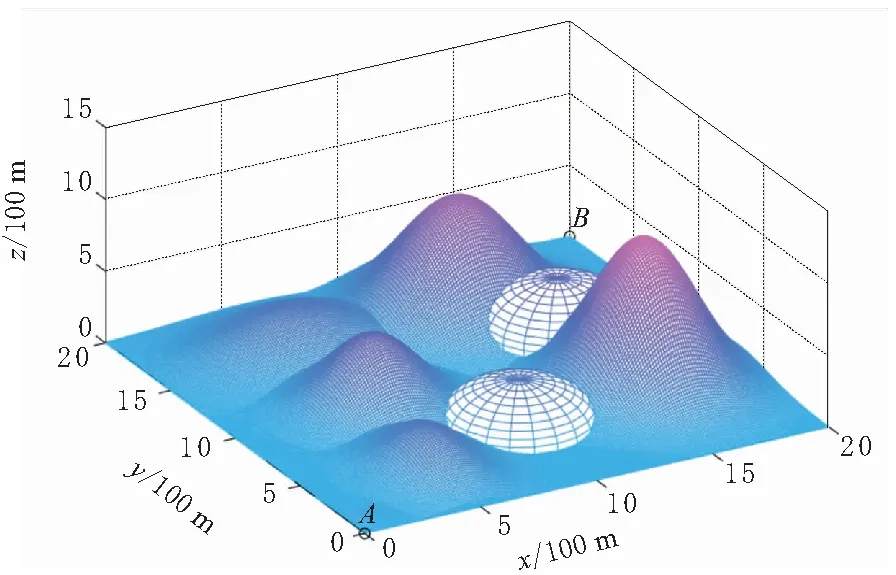
图1 任务场景
为控制此片区域,由n(n>1)架无人机组成的编队必须要反复检查控制点处情况。无人机从起始航空站A起飞进行侦察,侦察任务结束后飞入另一终点航空站B中,完成整个控制区域的侦查任务。飞行过程中考虑无人机自身性能约束、多无人机时间空间协同约束、航迹长度和雷达检测威胁等条件的情况,要求任意两机互不相撞,无人机总航程距离最短,同时使无人机尽量远离雷达,降低被发现概率,为多无人机编队规划出最优航迹。
2 建模分析
2.1 协同飞行约束条件设计
为保证所设计的航迹可满足多无人机飞行的要求,必须考虑一系列约束条件,本文从自身性能约束和协同约束2方面进行考虑。
2.1.1 自身性能约束
a.最大航程约束。
无人机自身携带油量一定,同时有配给的影响,因而存在航程上限,记最远航程为Lmax。假如某条航迹中包含m个航点,则要求该航迹段
(1)
li为该航程第i个航迹段的长度,本文取最远航程为80 km。
b.最大爬升角。
飞机的爬升角约等于俯仰角,为防止飞机失速,必须考虑无人机的最大爬升角γ。航迹相邻两节点的角度α满足
(2)
其中,第i-1个点坐标为(xi-1,yi-1,zi-1);第i个点坐标为(xi,yi,zi)。
本文取最大爬升角为30°。航迹规划还需考虑最大转弯角、最小步长和最小飞行高度等其他条件。由于所需侦察的控制点的位置相对分散,其余约束基本满足,暂不考虑。
2.1.2 协同约束
a.时间协同约束。
多机时间协同约束是指无人机间的出发时间和到达终点时间满足一定关系,从而达到多机协同合作的效果。本文中,起点航空站同时派出所有无人机,根据无人机飞行速度范围以及每个无人机的飞行距离,计算出每个无人机飞行所需的最长和最短时间。若能保证无人机同时到达航空站,则无人机的飞行到达时间区间必须存在交集,即可保证在一定时间范围内达到终点航空站。
假设第i-1架无人机的飞行速度为vi-1∈[vmin,vmax],飞行航程距离为Li-1,第i架无人机的飞行速度为vi∈[vmin,vmax],飞行航程距离为Li,则无人机飞行到达时间为
Ti-1∈[Ti-1,min,Ti-1,max]=[Li-1/vmax,Li-1/vmin]
(3)
Ti∈[Ti,min,Ti,max]=[Li/vmax,Li/vmin]
(4)
若2机满足时间协同条件,则
(5)
时间协同系数ft记为
(6)
可见,当ft小于0时,该航迹符合时间协同约束条件,且ft值越小,协同性能越佳。本文取飞机最小飞行速度vmin为80 km/h,最大飞行速度vmax为160 km/h。
b.空间协同约束。
空间协同约束表示无人机在执行任务的过程中,任意两机之间距离须不小于最小的安全距离dsafe。为避免无人机相撞导致任务失败,协同规划过程中考虑无人机避撞情况。记第i架无人机的位置为Xi,第j(i≠j)架无人机的位置为Xj,则两架飞机间的距离d应满足
(7)
当无人机结束各自航程,飞入终点航空站时,机间距离不可避免地不断减小,需调整安全距离dsafe,即
(8)
s为飞机与终点航空站之间的距离。同时,记本文中安全距离D=0.5 km,空间协同系数fs为
(9)
2.2 航迹代价模型设计
航迹规划的目的是以航迹代价模型作为评判标准,设计出最适合多无人机飞行的航迹,所以航迹代价模型的设计是航迹规划的核心。
a.航迹长度代价。
无人机飞行航迹长度越短,执行任务耗时减少,任务的成功率也相对更高。累加所有航迹段的长度,求得航迹长度代价函数。假设本次任务中,航迹段个数为n,航程距离总和为fL,则
(10)
li为第i个航迹段长度。
b.雷达威胁代价。
雷达的信噪比[10]S/N数值越小,则代表该目标被此雷达捕捉的概率越小,反之亦然。信噪比主要与目标和雷达的距离有关,对其原始公式[11]进行化简,得到
(11)
k为常数;dR为目标与雷达的距离。假设侦查雷达的天线可以360°扫描,能进行全方位侦查,则侦察到无人机的概率pR为
(12)
dmax为雷达所能探测到的最大距离;dmin为雷达一定能探测到目标的距离范围。如图2所示,O点为雷达位置。

图2 雷达作用范围
为计算航迹段的雷达威胁代价值,将该航迹段平均分为5份,计算出目标处于4个等分点和航迹段终点时被雷达侦查的概率,将5个值求和再取均值,求得该航迹段的雷达威胁代价。将所有航迹段的代价值相加,即得到该航迹的雷达威胁代价函数值。
3 NSGA-II算法设计
1994年,Deb等提出了NSGA(non-do-minated sorting genetic algorithm)算法。2001年,该团队为更好地解决多目标优化问题,在原先NSGA[12]算法基础上,提出了NSGA-II算法。NSGA-II算法降低了NSGA算法运算时间复杂度,提高了收敛性。该算法通过不断迭代,经过变异交叉选择等操作,最终生成1组Pareto最优解。
快速非支配排序和拥挤度距离计算是NSGA-Ⅱ算法的重要步骤,前者将目标解进行划分,生成Pareto前沿,Pareto前沿等级最优解组成Pareto解集,后者在前者的基础之上,计算每层Pareto前沿上相邻解的拥挤距离,算法则让Pareto等级更高,拥挤距离更大的解作为子代种群,再次进入循环,这样便同时保证了解的多样性和收敛性。
3.1 Pareto解集
多无人机协同航迹规划问题的目标函数之间通常存在冲突,难以得到使所有目标均达到最优的解。通过权衡各目标函数生成的Pareto解集[13],得到一系列“近似最优解”,即在约束条件允许的情况下,使得一个或多个目标条件达到最优,其余目标条件尽可能最优。在避免人为加权影响结果的情况下,可根据实际情况的具体要求选择不同的解。
假设该优化问题存在M个目标函数,N个决策目标,即
(13)
x为由N个决策目标组成的决策变量;y为目标向量。
定义1(Pareto支配关系),若存在决策变量x0和x1,使得
fi(x0)≥fi(x1)i=1,2,…,M
(14)
(15)
则称x0对x1是Pareto支配的。
定义2(Pareto前沿),受支配情况相同的解Pareto等级相同,构成Pareto前沿。
定义3(Pareto最优解集),对于一个决策变量,如果不存在能够支配它的其余变量,则为非支配解,称该变量为Pareto最优解。一系列非支配解所构成的集合即为Pareto最优解集。
3.2 种群自适应交叉和变异
种群个体的交叉和变异是产生新个体的重要来源[14],但是,盲目的进行交叉和变异可能导致最优解的破坏,迭代结果陷入局部最优。NSGA-II主要通过拥挤距离来判断种群的离散程度,本文将个体拥挤距离与该个体所在Pareto前沿的个体平均拥挤距离进行对比,并引入迭代因子i,确定交叉变异概率的大小,实现种群自适应进化,加强算法的搜索能力以及收敛方向的准确性。交叉概率pc和变异概率pm分别表示为
(16)
(17)
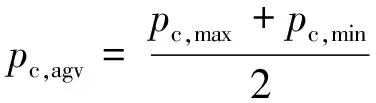
在种群迭代更新前期,进化个体具有较大的交叉和变异概率,满足种群个体多样性的要求,加强了算法的全局搜索能力;更新后期,进化个体的交叉和变异概率趋于平均值,算法着重于局部搜索,得到最终解。在原始的NSGA-II算法中,Pareto前沿的边缘个体拥挤距离设为无穷,为方便平均拥挤距离的计算,本次案例中设为0。
3.3 NSGA-II算法设计过程
3.3.1 染色体编码及种群初始化
本文使用双染色体编码方式[15]描述航迹。将所有的航点进行编号,一条染色体的基因表示航点(不包含起始点和终止点),另一条染色体的基因表示断点,该断点将表示航点的染色体进行分段,每一段表示1架无人机的航迹。假设现规划4架无人机的航迹,共侦查11个控制点,如图3所示。染色体1的基因表示航点,其基因数量与航点数相同;染色体2的基因表示断点,基因个数与无人机数量相同。染色体2中3表示无人机1需要依次侦查染色体1中前3个控制点,以此类推,从而得到所有飞机的航迹,其中,0表示出发的航空站,12表示终点航空站。
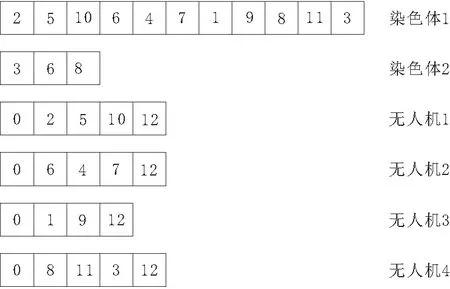
图3 双染色体表示航迹
本文采用随机数法进行种群初始化,同时考虑单无人机侦查的航点个数的最大和最小值。一方面可以一定程度上满足无人机最大航程的约束,另一方面可以使得无人机间分配的航点相对分散,生成的初代种群相对合理。本文设单机侦查航点数最大值Cmax=10,最小值Cmin=4。
3.3.2 选择操作
NSGA-II算法通过经典二元锦标赛选择法进行种群中优质个体的选择,本文对其进行如下修改。首先,剔除生成的种群中不满足自身性能约束的解,然后再对剩余的解使用二元锦标赛选择法:
a.若两解均满足协同约束,则先比较Pareto等级,选择等级更优者;若Pareto等级相同,则比较拥挤距离,选择拥挤距离较大的一方。
b.若有一解不满足协同约束条件,则选择满足协同约束条件的一方。
c.若均不满足协同约束条件,则进行协同系数比较,先比较空间协同系数,择优录取;若相同,再比较时间协同系数,择优录取。反复执行多次二元锦标赛选择法,直至所筛选个体数目与原种群个体数目相等。
3.3.3 交叉操作
进行交叉操作时,针对以航点作为基因的染色体进行双点交叉。随机选择2条航迹作为交叉对象,再随机选择相等数目的多个相邻航点进行交叉操作。以图3举例,交叉结果如图4所示。

图4 交叉操作
3.3.4 变异操作
变异操作分为航点变异和断点变异,2种变异相互独立,概率相同。航点变异方式有2种,发生变异时,算法会随机选择一种方式进行变异。一种是在同一条以航点作为基因的染色体随机选择2个航点,进行交换操作;另一种则是在染色体中随机选择1段航点进行翻转操作。断点变异则是重新生成断点染色体。同样以图3为例,航点变异如图5和图6所示。

图5 航点变异方法一

图6 航点变异方法二
3.3.5 精英保留策略
剔除所有不满足自身性能约束条件的解,再将剩余的解依据是否同时满足时间空间协同约束分为2类。对所有同时满足时间空间协同约束的第1类解依据Pareto等级和拥挤距离择优录取;若第1类解数量不足N,则在第2类解中继续挑选——先挑选满足空间协同约束的解,若挑选的解的总数还是不足N,则对第2类解中剩余解按照时间协同系数大小从小到大继续挑选。直至挑选的解的总数为N。
3.4 NSGA-II算法流程
a.种群初始化。确定雷达、航空站以及所需侦查的控制点(航点)的数量和位置,同时确定无人机数量以及单无人机侦查航点数的最大、最小值,并进行种群初始化,种群个体数目为N。计算初代种群个体(初代父代种群)的代价函数值及约束值,利用快速非支配排序得出每个个体的Pareto等级,并计算每个个体的拥挤距离。
b.优质解选择。对父代种群进行选择操作,挑选优良个体,组成个体数目为N的新种群。
c.交叉和变异操作。对新的种群个体进行自适应交叉和变异,生成个体数目为N的子代种群。
d.目标函数值和约束值计算。计算子代种群个体的2个目标函数值、2个性能约束值和2个协同约束值,进而计算每个个体的Pareto等级和拥挤距离。
e.生成新的父代种群。将父代种群和子代种群混合,使用精英保留策略筛选个体。当所筛选的个体数量累计为N时,结束筛选工作,构成新的父代种群。
重复b~e,直至达到终止条件,得到最终结果以及每代的最优结果。流程如图7所示。
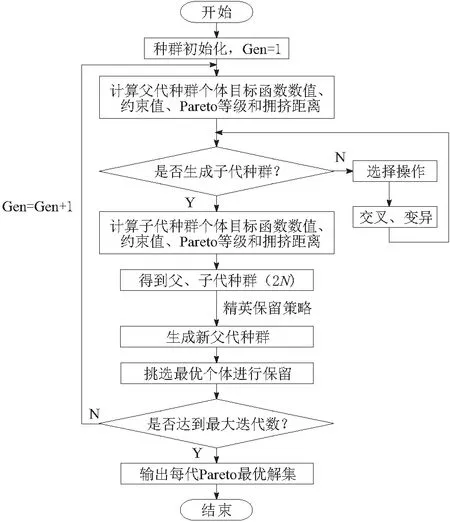
图7 NSGA-II算法流程
在算法的迭代过程中,剔除掉不满足自身性能约束的解,针对不满足协同约束条件的解不能轻易地剔除,一方面保证解的多样性,另一方面这些解中可能包含较优的部分,可进入下一轮迭代。
4 仿真验证
仿真平台为 Intel Core i7-7500U CPU、16GB内存、64位Win10操作系统的联想笔记本。编程工具为MATLAB R2016b(64位)。
4.1 参数设置
现给出待侦察控制点的位置坐标,无人机数量为3,敌方雷达数量为2,控制点位置暂不列出,航空站及雷达位置如表1所示。假设本例中使用一小型雷达,探测范围中dmax=3 km,dmin=0.4 km。

表1 参数设置
h1和h2分别为雷达所在地的当地高度,由地势方程决定。
选取算法迭代次数为500,种群个体数量为100,同时,算法中适应度函数取为2个代价函数的倒数,则满足适应度函数值越大,该解越优的情况。两者的适应度函数为
(18)
f1为航迹长度代价的适应度函数值;f2为雷达威胁代价的适应度函数值。因为雷达威胁代价相对航迹长度较小,则需调整系数,使得f1与f2在一张图中,便于实验观察,不影响分析结果。
4.2 有效性分析
使用自适应交叉变异的NSGA-II算法(算法1)与原始的NSGA-II算法(算法2),最终均规划出满足自身性能约束和协同约束的多组最优航迹。算法2的交叉及变异概率为定值,交叉概率为0.5,变异概率为0.055,数值大小与算法1平均交叉概率pc,agv、平均变异概率pm,agv相等。
将2个算法多组最优航迹的长度代价函数值f1、雷达威胁代价函数值f2和时间空间协同系数值ft、fs进行对比。其中,算法1的多组最优航迹的代价函数值和协同系数值均相同,即表明多组最优航迹虽航程不同,但最终导致的结果相同;算法2的多组最优航迹最终导致2种结果,构成2组代价函数值和协同系数值。结果如表2所示。

表2 算法结果对比
算法在迭代过程中筛除了不满足自身性能约束的解,最终代结果均满足自身性能约束,2种算法所得最终解均满足时间空间协同约束。虽然算法2的最终解可根据结果分为2类,可供决策者进行筛选,但算法1的解在适应度函数值上均优于算法2的解,代表算法1所求得的航迹拥有更短的航迹长度,受雷达威胁程度的更低。说明NSGA-II算法经过改进之后,增强了求解精度,自适应进化增强了算法对最优解的搜索能力。
由算法1所求得的最优航迹如图8所示,由算法2所求得的航迹如图9所示。可以看出,2组航迹的前半段类似,主要的区别在与后半段。

图8 算法1最优航迹
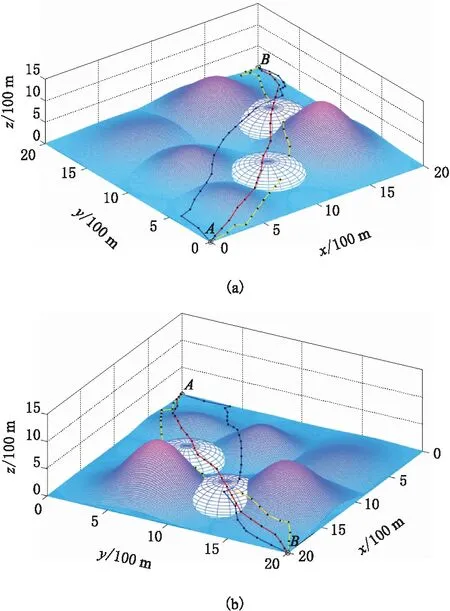
图9 算法2最优航迹
每代Pareto最优解的个数即为每代最优航迹数,算法1与算法2每代最优航迹数如图10所示。
从图10中可以发现,算法1的最优航迹数增加较快,在第23代达到最大值,随后保持不变,即说明已找到最优解集。算法2的最优航迹数较不稳定,在算法迭代运算中期达到最大值,随后出现明显回落,振荡严重,说明一直未能找寻最优解集,最终在第366代保持稳定,此时找到最优解集,且最优解个数较少。

图10 最优航迹数比较
可以看出,改进后的算法1寻优能力远大于算法2,不仅可以寻找到更优解,寻找最优解集的速度和数量明显优于算法2。
4.3 收敛性分析
记录下每代种群的Pareto最优解集中适应度函数最大值,以及协同系数最小值,通过最值判断算法的寻优情况。算法1的最值情况如图11所示,算法2的最值情况如图12所示。

图11 算法1适应度函数及协同系数最值变化情况

图12 算法2适应度函数及协同系数最值变化情况
对图11和图12分析结果如下:
a.算法1的收敛情况明显优于算法2。算法1中代价函数值f1、f2和时间空间协同系数ft、fs从第15代开始便保持稳定,而算法2则一直处于寻优状态,在第320代后保持代价函数值和协同系数稳定。可以看出,改进后的算法1收敛速度优于算法2,稳定性更好,且收敛的最终结果更优,收敛方向的准确性更优。
b.针对该多约束条件下多目标多变量问题,算法为寻求最优解,约束条件和适应度函数之间往往也存在冲突。在算法2的第350代解中,航迹长度代价函数值f1变大,时间协同系数变小,说明最优航迹长度变短,时间协同性能增强,与此同时,雷达威胁代价函数值f2变小,说明受雷达威胁程度的上升。说明规划出的最优航迹通过增加无人机受雷达威胁程度,可以获得更短的路径和更好的时间协同性能。
5 结束语
为在三维空间中实现对多无人机的航迹规划,本文采用双染色体编码方式表示航迹,对无人机飞行的航迹长度、航迹安全性、自身性能约束以及时间空间协同性等方面进行综合考虑,并且针对NSGA-II算法进行改进:加入了自适应进化策略,同时优化了种群个体选择操作及精英保留策略,避免盲目进化,加强算法的求解精度和收敛性。仿真实验证明,改进后的NSGA-II算法增强了算法的寻优能力,收敛速度变快,收敛方向的准确性明显提升,可以更好地解决多无人机的航迹规划问题。未来研究,一方面注重于对选择操作等环节的不断优化,使得算法运行效率的不断提升;另一方面,结合更多复杂环境,注重于航迹规划中时间空间约束条件的创新。

