微电阻率扫描测井仪极板推靠机构研究

宋 红，张魁峰，张春琳，唐道临，任 涛

(1.西安石油大学 机械工程学院，陕西 西安 710065；2.成都北方石油勘探开发技术有限公司，四川 成都 610051；3.延长油田股份有限公司 物资装备部，陕西 延安 716000)

引 言

微电阻率扫描测井仪是当今世界最先进的成像测井仪之一[1]。微电阻率扫描测井仪能够提供井眼地层高分辨率、大动态范围微电阻率成像，在复杂地层的勘探开发中发挥了重要作用[2]。微电阻扫描成像测井技术还具有高分辨率、高井眼覆盖率和直观可视等特征[3]。套后电阻率测井技术能有效地用于油气藏动态监测、确定含油饱和度等[4]。目前，关于测井仪推靠机构的运动学及动力学分析方面的研究较少。任涛等人[5]利用复数矢量法进行新型分动式六臂井径测井仪推靠系统运动学及动力学分析，得到了该测井仪推靠机构各杆件的位置方程、速度方程及加速度方程；任涛等人[6]用矩阵解析法对微球聚焦测井仪推靠系统运动学进行分析，从而得到该测井仪推靠机构各杆件运动参数，真实反映推靠机构的实际运动状况。

推靠机构运动性能的好坏直接影响测井数据的准确性[5]。本文就微电阻率扫描测井仪推靠机构运动学及动力学进行研究，运用矩阵解析法得到微电阻率扫描测井仪推靠机构各杆件的位置方程、速度方程及加速度方程，并对各杆件进行动态静力学分析得到了动态静力学方程；运用Adams对微电阻率扫描测井仪推靠机构进行建模，并虚拟仿真其运动，进一步分析了其运动规律，为后续推靠机构动力学分析及结构参数优化提供了理论依据[7]。

1 微电阻率扫描测井仪物理模型建立

本文使用Solidworks对微电阻率扫描测井仪进行建模，如图1所示。推靠机构机械传动部件主要包括：电机、泵体、液压缸、活塞、主力杆、顶杆、蝶形弹簧、主推杆、支臂、辅助杆、调节杆、极板和杆系架。

图1 微电阻率扫描测井仪三维实体模型

本文所提出的新型推靠机构的主要优点在于：与原推靠机构相比，该新型推靠机构在测相同大小的井径时所需的碟簧推靠力相差不大，但新型分动式推靠机构顶杆对密封圈没有挤压，而原机构顶杆对密封圈存在非均匀挤压，类似于滚动轴承的受载，容易导致密封失效，并且新型分动式推靠机构采用了带渐开线型凸轮的主力杆，其机械效率更高。

2 推靠机构打开过程运动学及动力学分析

为了保证微电阻率扫描测井仪具有确定的运动，需要计算该推靠机构的自由度。如图2所示，该机构自由构件数n为6(即主推杆1，支臂2，主力杆3，顶杆4，极板5，辅助杆6)，低副pl个数为7(5个转动副A、B、C、D、E和2个移动副H、J)，高副ph个数为2(凸轮副L和槽销副B)。根据机构自由度计算公式得该机构自由度F为2。

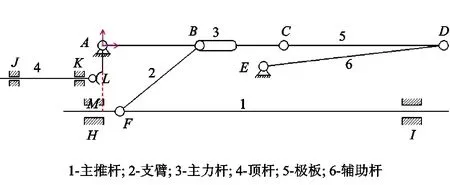
图2 微电阻率扫描测井仪推靠机构简图

由机械原理可知，如果机构的原动件数目小于机构的自由度，机构运动将不完全确定[8]。微电阻率扫描测井仪推靠机构的工作过程分为打开过程和测量过程。推靠机构打开过程中，支臂与主力杆铰接处，在蝶形弹簧预紧力的作用下，销钉只转动，并没有和销槽发生相对移动，所以销钉和销槽在打开过程中形成了一个转动副。于是，机构高副个数为1(凸轮副L)；低副个数为8(2个移动副H、J，6个转动副A、B、C、D、E、F)。因此，该机构在打开工作过程中自由度为1。测量过程中，由于电机停止工作，主推杆1停止移动；自由构件数为5(即支臂2，主力杆3，顶杆4，极板5，辅助杆6)，高副个数为2(槽销副B、凸轮副L)；低副个数为6(1个移动副J，5个转动副A、C、D、E、F)。该机构测量工作过程中自由度也为1。所以，微电阻率扫描测井仪推靠机构两种运动都是确定状态。

2.1 推靠机构打开状态运动学分析

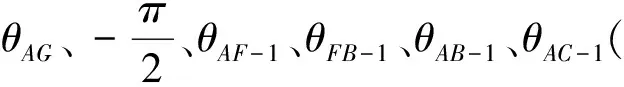
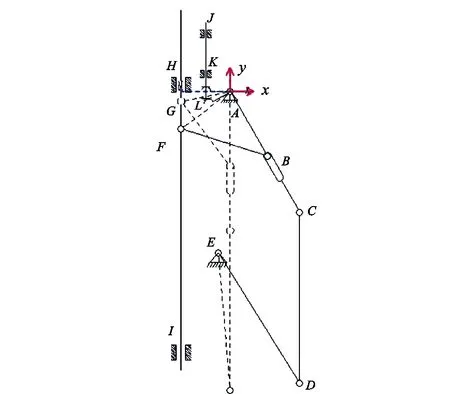
图3 推靠机构打开(收拢)过程简图

2.1.1 推靠机构打开过程中各构件位置分析

根据封闭矢量多边形投影法，连接AG、AF，封闭矢量方程式为

lAF-1=lAG+lGF=lAB-1-lFB。

(1)

式(1)中各矢量在x、y轴上投影，得到F点的位置方程：

(2)

主力杆C点的位移：

(3)

主力杆质心的位移：

(4)

极板质心的位移：

(5)

辅助杆质心的位移：

(6)

2.1.2 推靠机构打开状态速度分析

式(2)对时间t求一阶导数，整理成矩阵形式为

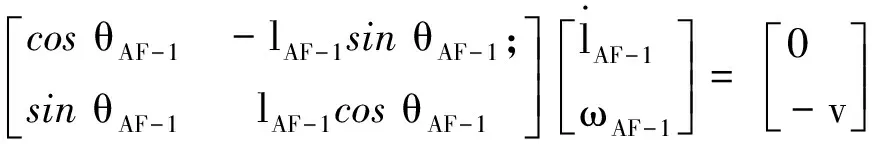
(7)

(8)

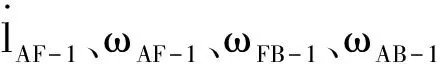
在解得以上各未知量后，可得出各点速度方程：

主推杆F点速度为

(9)

式(3)对时间t求导，得主力杆C点速度为

(10)

式(4)对时间t求导，得主力杆质心速度为

(11)

式(5)对时间t求导，得极板质心速度为

(12)

式(6)对时间t求导，得辅助杆质心速度为

(13)

2.1.3 推靠机构打开状态加速度分析

式(2)对时间t求二阶导数，整理成矩阵形式为

(14)

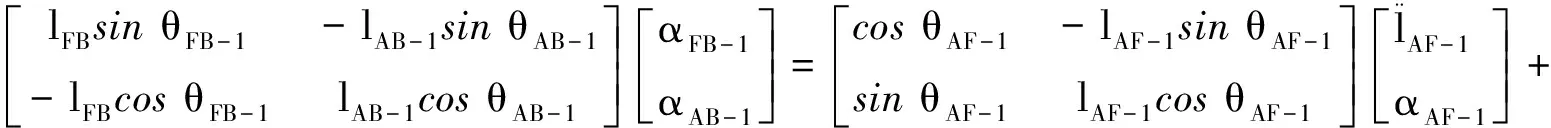
(15)

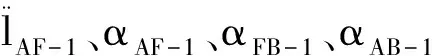
在解得以上各未知量后，得到各点加速度方程：

主推杆F点加速度为

(16)

式(10)对时间t求导，主力杆C点加速度为

(17)

式(11)对时间t求导，得主力杆质心加速度为

(18)

式(12)对时间t求导，极板质心加速度为

(19)

式(13)对时间t求导，辅助杆质心加速度为

(20)

2.2 推靠机构打开状态动力学分析

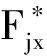
在运动学求解部分已经得到了各杆件的加速度，从而可求出各杆件所受的惯性力以及惯性力矩。根据支臂受力情况，分别以各构件为研究对象，建立动力学平衡方程。

(1)支臂FB受力情况如图4所示。动力学平衡方程为

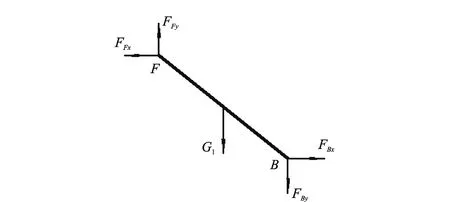
图4 支臂FB的受力分析简图

(2)主力杆LAC受力情况如图5所示。动力学平衡方程为

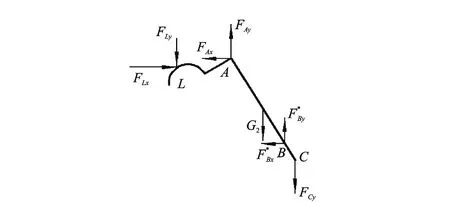
图5 主力杆LAC受力分析简图

(3)极板CD受力情况如图6所示。动力学平衡方程为

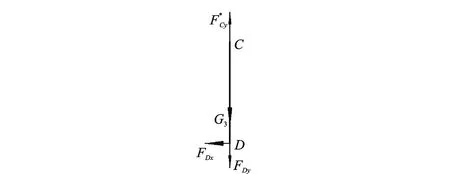
图6 极板CD受力分析简图

∑MC=FDxlCD-JCαCD=0。

(4)辅助杆ED受力情况如图7所示。动力学平衡方程为

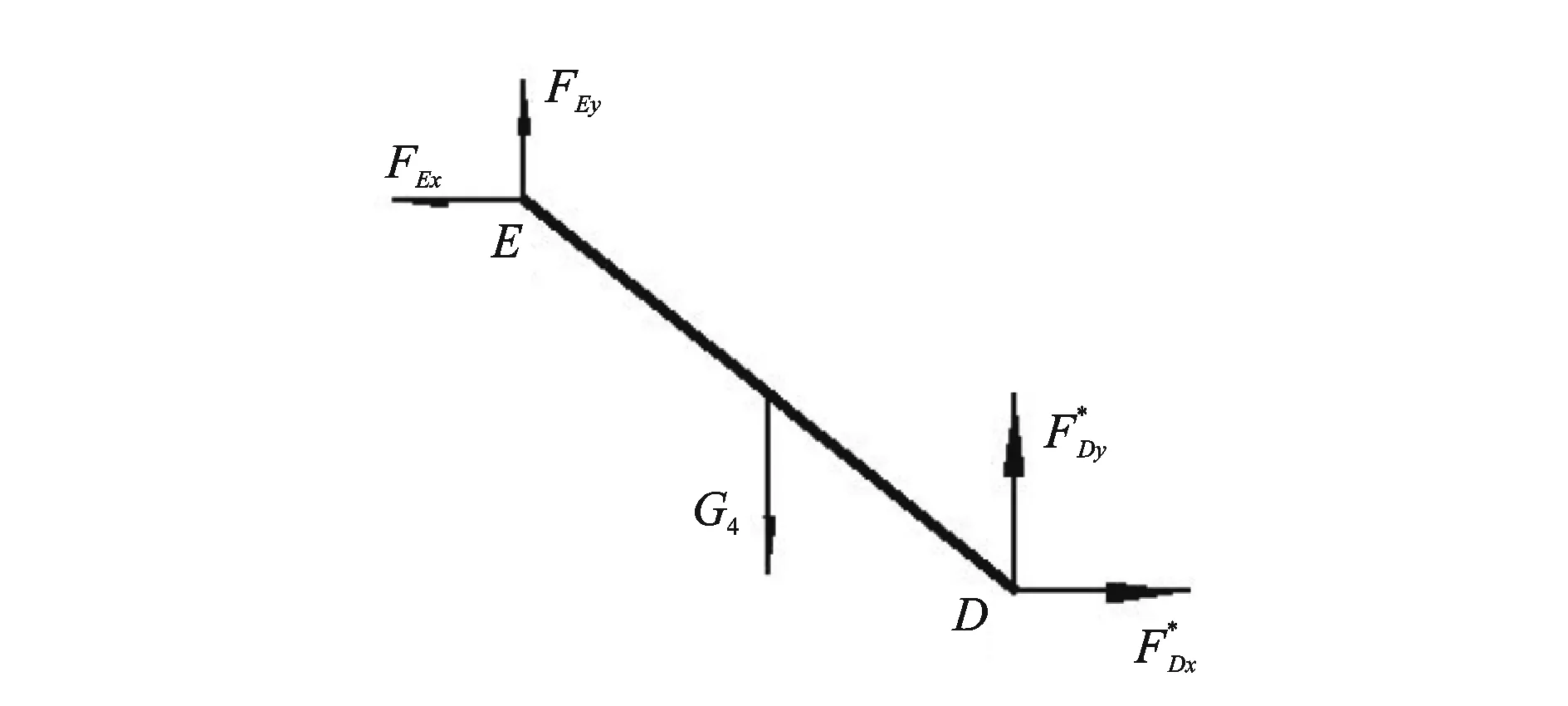
图7 辅助杆ED受力分析简图

3 推靠机构贴壁测量过程运动学及动力学研究

3.1 推靠机构贴臂测量过程运动学分析

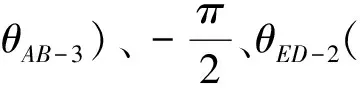
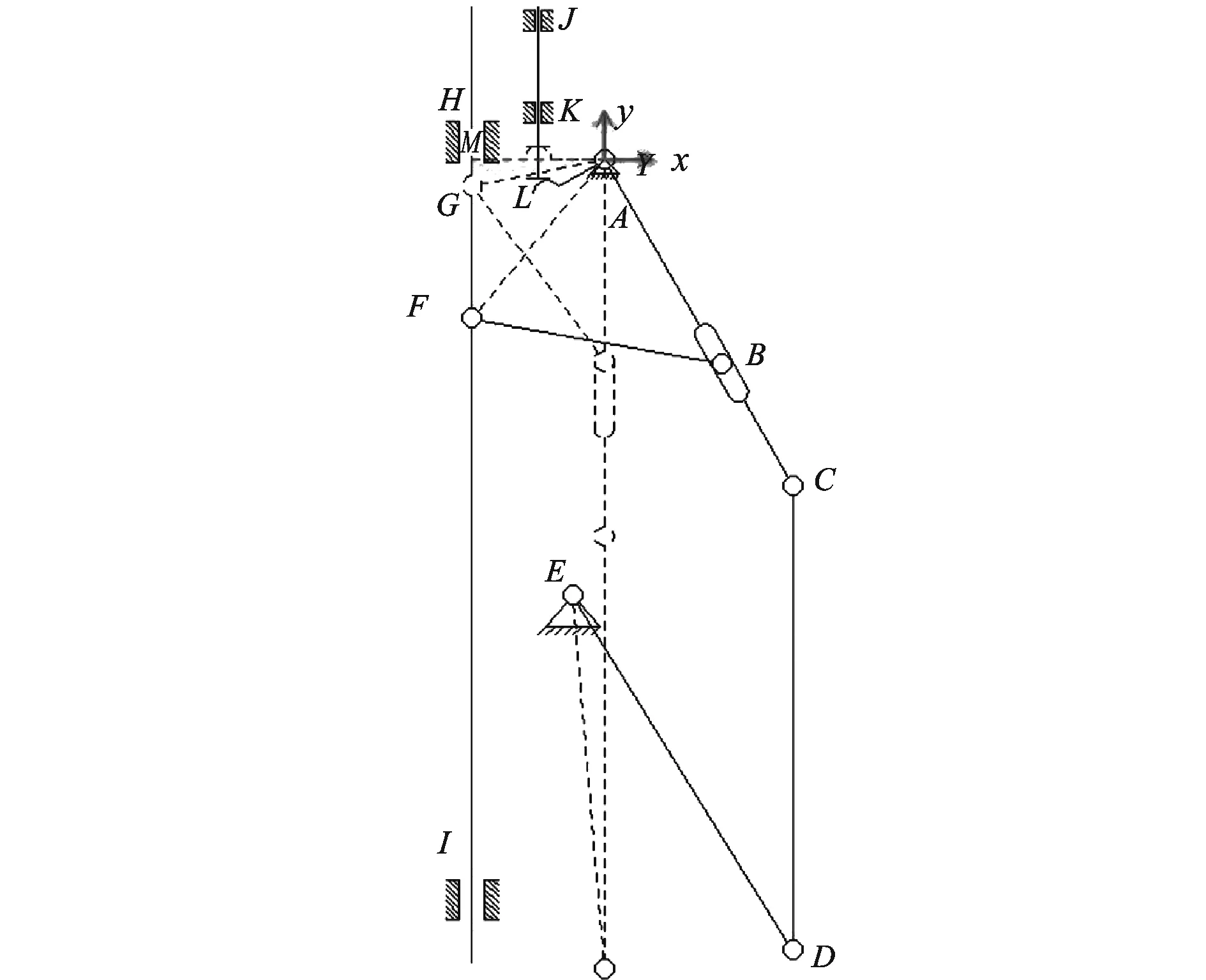
图8 推靠机构贴壁测量过程运动分析简图

3.1.1 推靠机构贴臂测量过程位移分析

根据封闭矢量多边形投影法，连接AF，封闭矢量方程式为

lAB-2=lAF-2+lFB-2。

(21)

式中：各矢量在x、y轴上投影，得到B点的位置方程：

(22)

式(22)中:θFB-2、lAB-2未知，可由式(22)解得。从而得到推靠机构各点在贴臂测量过程中的位置方程：

主力杆C点位移为

(23)

主力杆质心位移为

(24)

3.1.2 推靠机构贴壁测量过程速度分析

式(22)对时间t求一阶导数，整理成矩阵形式为

(25)

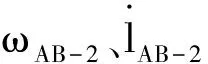
式(22)对时间t求导，主力杆B点速度为

(26)

式(23)对时间t求导，得主力杆C点速度为

(27)

式(24)对时间t求导，得主力杆质心速度为

(28)

3.1.3 推靠机构贴壁测量过程加速度分析

式(22)对时间t求二阶导数，整理成矩阵形式为

(29)

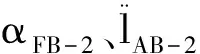
式(26)对时间t求导，主力杆B点加速度为

式(27)对时间t求导，主力杆C点加速度为

(31)

式(28)对时间t求导，得主力杆质心加速度为

(32)

测量过程动力学分析与打开过程类似，只是多了井壁对极板的作用力，这里不再推导。

4 推靠机构运动学仿真

4.1 分动式推靠传动机构仿真模型建立及运动学仿真

在Solidworks中建立微电阻率扫描测井仪的三维简化模型,并只保留微电阻率扫描测井仪推靠机构,将建立的三维模型另存为Parasolid(*.x_t)格式输出,然后进入Adams环境中,通过import打开已保存的模型[9]。

本文设计的微电阻率扫描测井仪主要适用于10 in(即254 mm)裸眼井。工作过程中，分动式推靠机构3个极板的运动状态是相同的，所以通过简化模型，运用Adams中的Adams/View模块只对该推靠机构中的一组机构进行结构参数化设计[10-11]。

4.1.1 推靠传动机构几何模型

已知AL=28 mm、AM=51.1 mm、MG=54.5 mm，主推杆速度v=2.5 mm/s。

(1)推靠传动机构的创建

图8中每个构件基本参数：主力杆AC长284 mm，支臂FB长148 mm，极板CD长410 mm，主推杆HI长450 mm。

(2)推靠传动机构运动副的创建

实体模型建立后，根据推靠机构各部件之间的连接关系和实际工况添加约束和驱动。建立主推杆和外壳的移动副，顶杆和地面之间的移动副，主力杆和地面之间的转动副，主力杆和支臂之间的转动副，支臂和主推杆之间的转动副。

(3)推靠传动机构运动驱动的创建

建立主推杆和地面的平移驱动并修改运动函数为2.5 * time，创建完成后的仿真模型如图9所示。

图9 推靠机构仿真模型

4.1.2 仿真与测试

设置仿真终止时间为5 s，仿真步数为100。图10为推靠机构中主力杆在x轴方向位移曲线。图11为主力杆角速度和角加速度曲线。图12 为主力杆C点速度、加速度曲线。

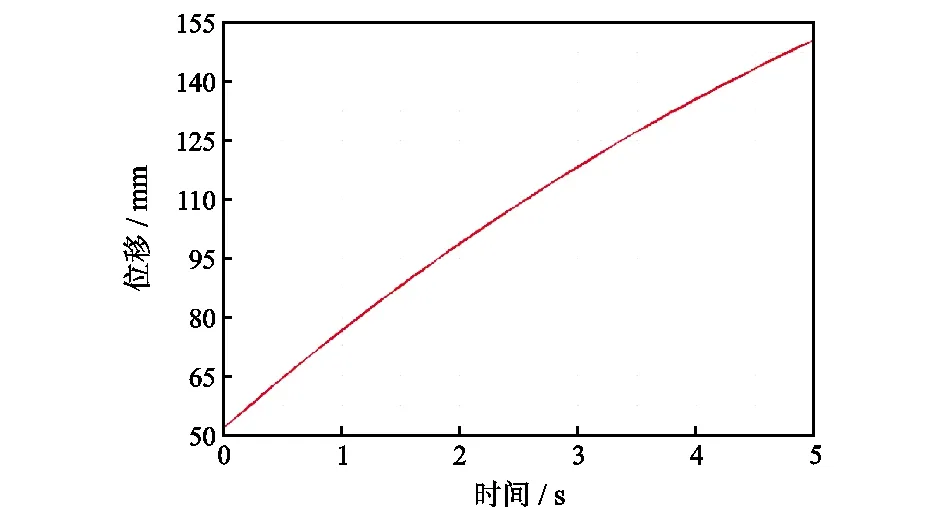
图10 推靠机构中主力杆在x轴方向位移曲线

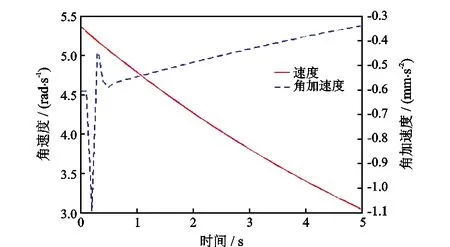
图11 主力杆角速度和角加速度曲线

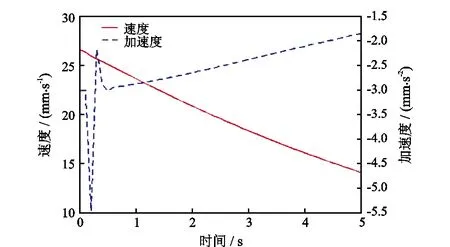
图12 主力杆C点速度、加速度曲线

由图10可知，主推杆以2.5 mm/s的速度运动时，主力杆上C点运动到10 in井壁停止所需时间约为3.4 s。

由图11可知，主力杆打开时的角速度逐渐减小，其角加速度在开始很短时间内发生突变，这是由于各铰接点间存在一定的间隙，仪器突然启动时会发生一定程度的振动。

由图12可知，主力杆端点C点的速度逐渐减小，验证了设计方案和理论模型的合理性，即在和井壁接触时的速度最小，从而井壁对测井仪的冲击更小。其加速度在仪器启动的瞬间发生突变，说明仪器突然启动会引起振动与冲击。

A点、F点支反力、力矩分别如图13、图14所示。

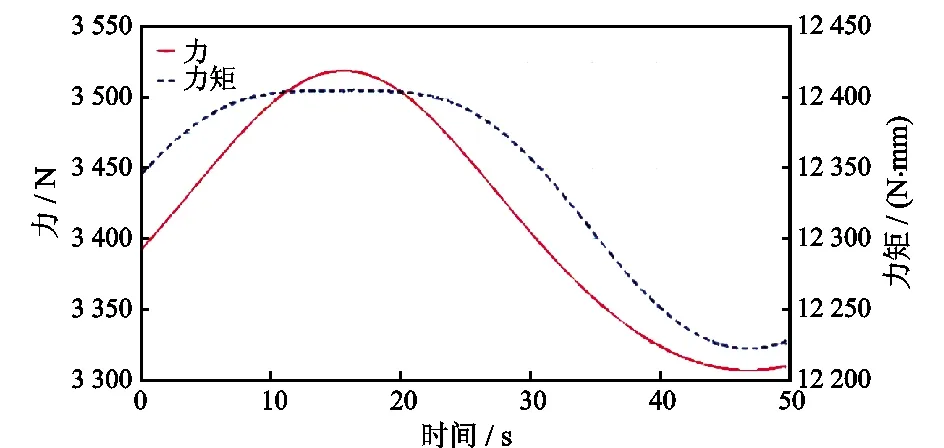
图13 A点支反力、力矩

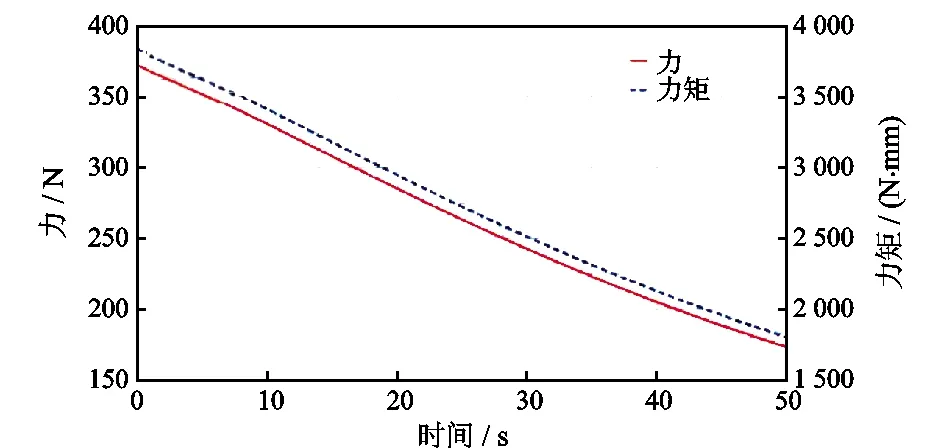
图14 F点支反力、力矩

从图13可以看出，A处的销钉所受的最大剪力不超过3 525 N，该值可作为销钉强度设计的理论值。

从图14可以看出，F处的销钉所受的最大剪力不超过380 N，该值可作为销钉强度设计的理论值。

5 结 论

(1)通过分析研究发现，本文所提出的一种新型推靠机构在打开和贴臂测量两种工作过程中的运动都是确定的，且该机构相较于原机构，极板贴靠井壁时的瞬时速度更小，则井壁对极板的冲击更小，有益于延长极板的使用寿命。

(2)本文对新型推靠机构各杆件的运动参数做了详尽的理论分析和仿真，为国内带推靠装置的测井仪器的设计提供了理论依据和参考。

(3)通过Adams虚拟仿真得出了机构的运动规律曲线等，对推靠机构的设计具有指导意义；机构运动过程中所受的外界阻力主要为井壁的摩擦阻力，由于条件所限未能获取到相关实验数据，在仿真实验中未考虑，所以仿真结果必然存在一定的误差。