基于随机森林的致密储层分类——以延安气田东部盒8段为例

王 妍，王若谷，魏克颖，卢海娇，熊小伟，张天杰

(1.西安石油大学 石油工程学院，陕西 西安 710065；2.陕西延长石油(集团)有限责任公司 研究院，陕西 西安 710006；3.中国石油长庆油田分公司 第三采气厂，内蒙古 乌审旗 017300；4.中国石油长庆油田分公司 长北作业分公司，陕西 西安 710000；5.中国石油长庆油田分公司 第三采油厂，宁夏 银川 750000；6.中国石油长庆油田分公司 第一采油厂，陕西 西安 710000)

引 言

近年来，我国致密砂岩研究已获得突破。在多个盆地，致密砂岩已成为增储上产的重要领域。但是我国致密砂岩油气的形成和分布复杂、多变，资源品质较差，开发利用经济敏感性强，需要在经济与技术策略相对一致的情况下分阶段、分类型开发[1-3]。储层分类是按照储层优劣等级对研究区储层进行排序，是开发选区、井位部署、产能预测以及开发方案制定的重要依据[4-5]。不同于常规储层，致密砂岩储层孔喉半径多为微米级。孔隙结构复杂的特殊性对致密砂岩储层分类计数的精度和方式提出了更高的要求[6-10]。

常规的储层分类方法主要有3种。第一种是单参数分类法，即仅考虑单一参数进行储层分类，如：根据渗透率大小将储层分为高渗、中渗以及低渗储层[11-12]，或根据压汞实验中进汞饱和度达到35%时，对应的喉道半径r35的大小进行储层岩石物理分类[13]；第二种是基于现场实际的地质经验法[14-15]，对研究区砂体特征、沉积相带展布、储层物性特征及气水分布进行分析，在孔隙结构分类的基础上，综合考虑上述两种或若干种特征参数，对研究区储集层进行分类；第三种是基于数理统计学的多元统计分析法[16-18]，借助地质统计学、聚类分析、模糊识别等数学方法，对储层进行定量表征和分类评价。

上述三类分类方法有各自的适用性，也有一定的局限性，具体表现在：(1)影响储层品质的因素多，各因素相关关系复杂，简单利用单一参数分类法不能准确反映储层的真实情况。(2)不同区块地质特征差异显著，源于具体研究区勘探生产实践的地质经验法仅能充分考虑本区储层成因的影响因素，在本区应用效果良好，但不能建立普适的评价方法和标准。(3)前人采用多元统计分析法对储层进行分类的过程中，往往重数据统计而轻数据分析。简单的数据统计不能满足储层分类的精度要求。

致密砂岩储层孔喉结构复杂、井间产能差异明显，因强非均质性而不能使用单一参数评价储层类型，同时也使得各个评价参数均具有一定的独立性。多个评价参数彼此相关关系不明显、主次不清，使分类结果表现出模糊性、多解性，评价效果主观性强，不能满足储层分类的要求。因此，针对致密砂岩储层，需要在多变量分析的基础上，根据数据关系的密切程度对其进行分类[19-21]。

选择延安气田上古生界二叠系盒8段致密砂岩的岩心压汞数据，通过主成分分析和随机森林算法对其分析，研究适用于致密砂岩储层的分类方法。延安气田盒8段致密砂岩气藏分布广，具有低压、低产、低丰度等特征，有效单砂体规模小、单井产量变化大[22]，因此，需要在勘探开发阶段进行储层分类，优化开发方案，分阶段、分类型开发。本文提出使用随机森林的致密储层分类评价方法，以期解决致密砂岩储层分类评价涉及指标多、需要借助压汞曲线判别储层类型、耗费时间和人力多的问题。

1 计算原理

1.1 主成分分析法

主成分分析法(Principal Component Analysis，PCA)是一种常见的数据分析方式，通过正交变换将一组线性相关的原始数据变换为一组由线性无关变量表示的数据，可用于提取数据的主要特征分量，常用于高维数据的降维[23]。假设有m条n维的零均值化样本数据X，

(1)

ΛE=CE。

(2)

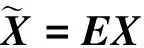
1.2 基于CART决策树的随机森林

随机森林算法是一种有监督的集成学习方法，属于Bagging方法(Bootstrap Aggregation,自举汇聚法)。随机森林由多棵决策树构成，决策树可以是ID3，C4.5或CART等类型，决策树彼此没有关联。通过随机重复抽取N个训练样本，在森林中并行构建M棵决策树。森林中的每一棵决策树都可以进行分类，事实上，这就形成了M个分类器。最终，测试样本的分类是根据这M个分类器的投票结果，选择分类结果中出现次数最高的作为随机森林的最终分类结果。随机森林算法借助森林中决策树的随机性，降低决策树的深度，并在训练时避免分类模型的过拟合，能提高模型预测准确性，具有良好的适应能力[24]。

(1)CART决策树

CART(Classification and Regression Tree)决策树是一种二叉决策树，既能处理分类又能处理回归问题。本文构建的CART决策树，使用基尼系数(Gini)来选择最好的数据分割特征，基尼系数描述的是纯度，与信息熵的含义相似。

构造训练集用来训练随机森林分类模型。假设在训练集S(C,D)中有|S|个样本，那么|S|的数量是来自M个储层的共计L1条压汞数据。其中，C为样本的条件属性，即识别有效储层的标准，也称为储层特征；D为决策属性，即储层的分类类别。

可将储层识别为Ⅰ类(记为1)、Ⅱ类(记为2)、Ⅲ类(记为3)和Ⅳ类(记为4)。因此，将决策属性分为4类，记为Do(o=1,2,3,4)。储层特征Cj将训练集S划分为Ⅰ、Ⅱ、Ⅲ和Ⅳ类储层子集。在子集Sg(g=1,2,3,4)中有|Sg|样本，子集Sg的基尼系数定义

(3)

其中,pog是子集Sg中Do类的概率。基尼系数越小，说明子集的纯度越高，信息增益越大。如果子集Sg中所有样本都属于同一类，则基尼系数为零。

训练集S的基尼系数

(4)

当使用CART算法进行节点划分时，需要计算各特征的基尼系数值，并选择最小的基尼系数值进行划分，然后递归构造决策树，生成分类规则。

(2)每棵决策树的训练子集生成

在随机森林分类模型中，每棵决策树都有一个对应的训练子集。如果存在N棵决策树，则需要从原始训练集中随机选择N个训练子集。本文采用Bagging(bootstrap aggregation)方法，这是一种有放回的抽样方法。在初始训练集S中采样，生成一系列训练子集S*。步骤如下：(a)从S中随机选取一个样本，放入S*；(b)将样本放回S中，以便在下一次取样时仍可选择该样本；(c)重复步骤(a)到(b)i次，得到包含i个样本的子集S*。S*是决策树的训练集；(d)重复步骤(a)至(c)N次，以获得N个子集S*用于训练N棵决策树。

(3)随机森林构建

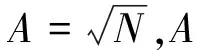
Tree(x,ξk)。

(5)

其中，Tree(x,ξk)为第k棵决策ξk树；x是输入变量，是独立且同分布的随机变量，表示决策树中使用的参数集。通过以上两个随机选择过程建立了一个包含N棵决策树的随机森林，表示为{Tree1(x),Tree2(x),…,TreeN(x)}。

(4)随机森林的决策

构造测试集用于模型验证。假设测试集S′中有|S′|个样本，那么|S′|的数量是来自M个储层的共计L2条压汞数据。在随机森林分类模型中，储层的类别首先由每棵决策树分类，表示为{Y1，Y2，…,YZ}，然后将每棵决策树的结果通过一种组合策略进行组合，得到最终的分类结果。最常用的组合策略是投票法。该方法选择分类结果中得票最高的作为最终的分类结果。同时，通过随机森林分类模型得到第k个样本属于Do类的概率，表示为Pko。

1.3 分类性能的评价方法

储层分类评价将数据分为两类：训练集和测试集。训练集用于构建模型，通过测试集对模型进行最终评估。一般使用精度、混淆矩阵等评价分类的性能。其中，精度为所有预测正确的样本数与测试集样本数的比值。同时，随机森林算法可采用袋外误差(Out-of-Bag error，OOBe)来衡量自身的性能，评估模型准确度。因此，本文采用精度、OOBe曲线和混淆矩阵来评价分类的效果。

在研究区应用随机森林算法进行储层分类，其流程如图1所示。具体步骤如下：

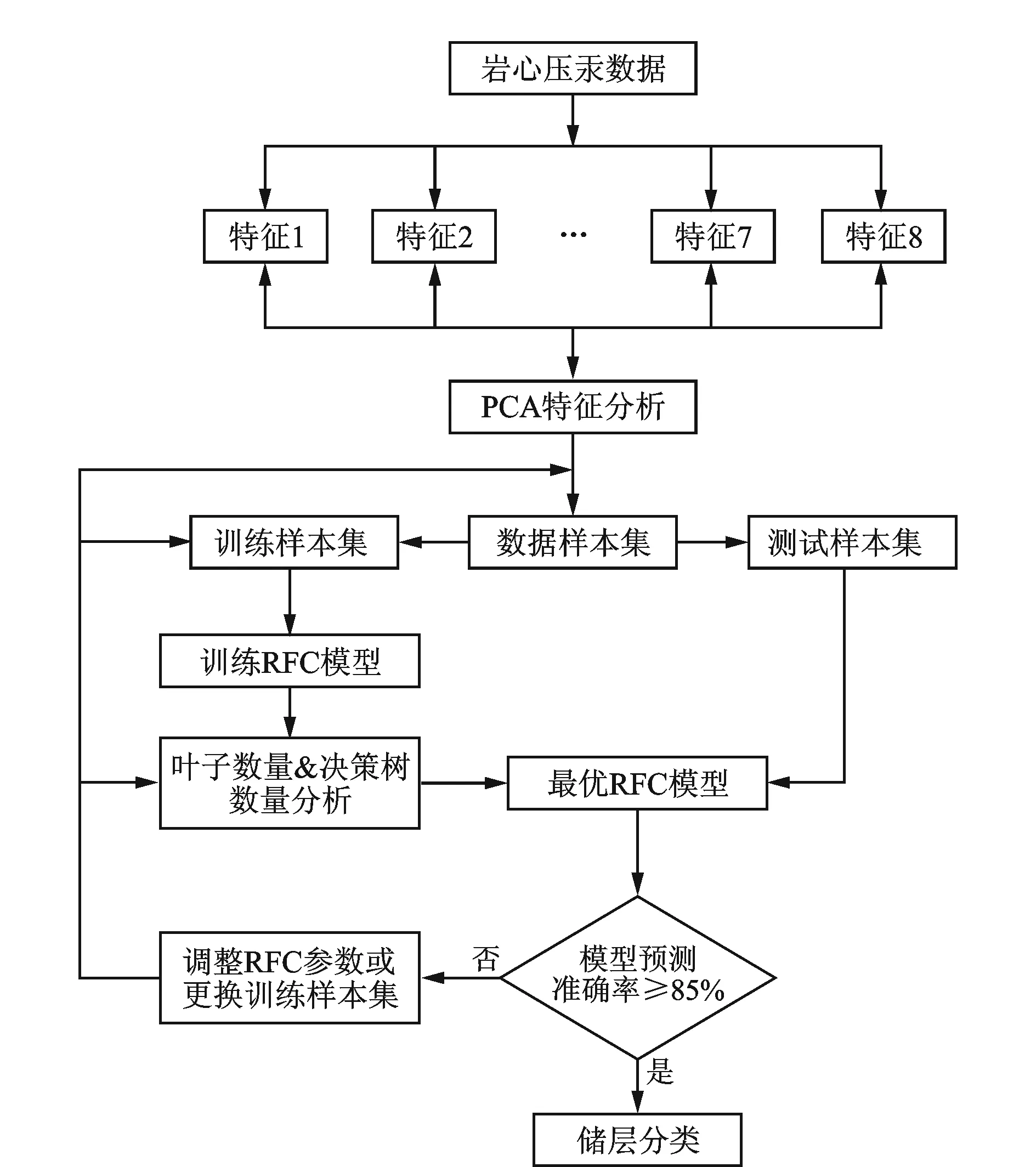
图1 主成分分析-随机森林储层分类流程

(1)对岩心压汞数据中反映储层微观孔隙结构的特征参数进行归一化处理，利用PCA分析这些特征的主成分因子，选取因子值最大的若干个特征参数作为储层分类的依据。

(2)利用分析后的数据样本集，采用有放回的随机抽样方式，构建若干个决策树的训练样本子集。

(3)使用所构建的训练样本子集，逐一地训练生成若干棵决策树，这些决策树就构成了用于储层分类的随机森林模型(RFC模型)。

(4)通过训练样本集的分类精度、袋外误差来分析随机森林分类模型决策树数量和叶子数量对分类结果的影响，选取最优的参数形成最终随机森林分类模型。

(5)使用最终随机森林分类模型对测试样本集进行储层分类。如果模型预测精度高于85%，则达到储层分类算法的设计要求。如果预测精度低于85%，则通过调整分类模型的超参数(样本特征数量、训练样本集抽取数量、决策树数量和叶子数量)来优化模型。

2 实验验证

2.1 数据来源

以延安气田东部下石盒子组致密砂岩储层作为研究目的层。延安气田东部位于鄂尔多斯盆地东南部(图2)，地处陕北斜坡一级构造单元，其构造形态呈西南倾向的宽缓大型单斜，局部发育小型鼻状隆起。目前已发现二叠系下石盒子组盒8段、山西组和石炭系本溪组等多个含气层系。截至2020年底，延安气田致密砂岩储气量达7 635×108m3，其中盒8段致密砂岩探明天然气地质储量近1 447×108m3，是目前鄂尔多斯盆地上古生界最大的致密砂岩气藏之一。

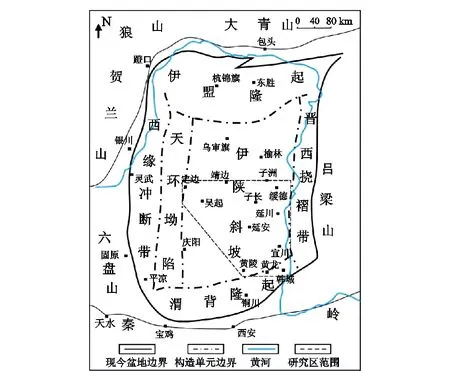
图2 研究区构造位置

延安气田盒8段沉积期主要发育辫状河三角洲前缘亚相(图3)。受控于沉积相带的展布，盒8段储层主要分布于水下分流河道。储层岩石类型多样，岩屑砂岩、岩屑石英砂岩和石英砂岩均有发育(图4)。孔隙类型以次生溶孔、晶间孔为主，孔喉结构多以细孔—细微喉道和微孔—细微喉道组合为主，对应的压汞曲线多为Ⅱ型和Ⅲ型(图5)。

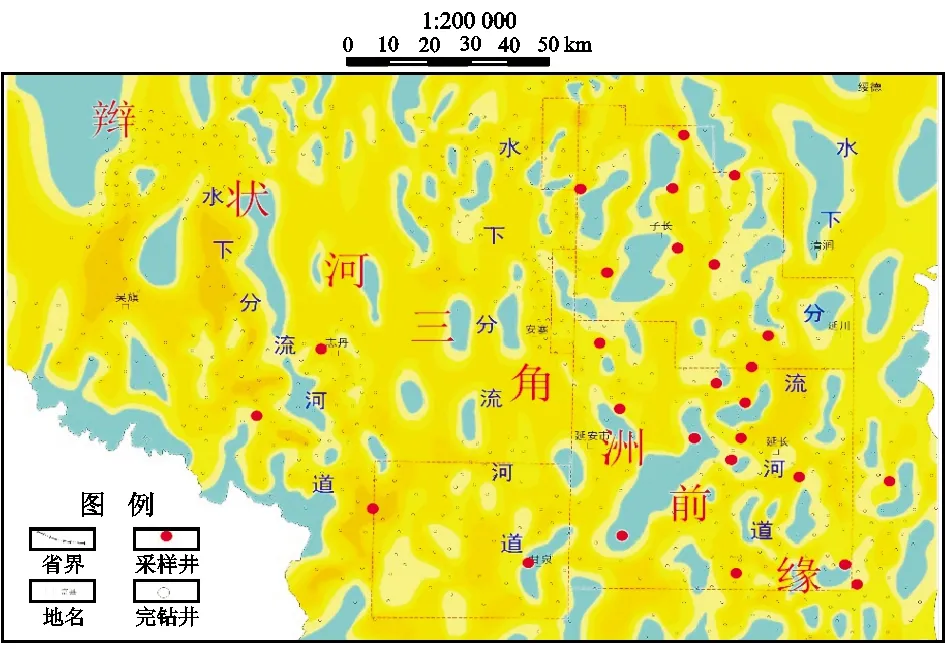
图3 延安气田东部盒8储层沉积相及采样位置

图4 研究区不同类型储层孔隙特征

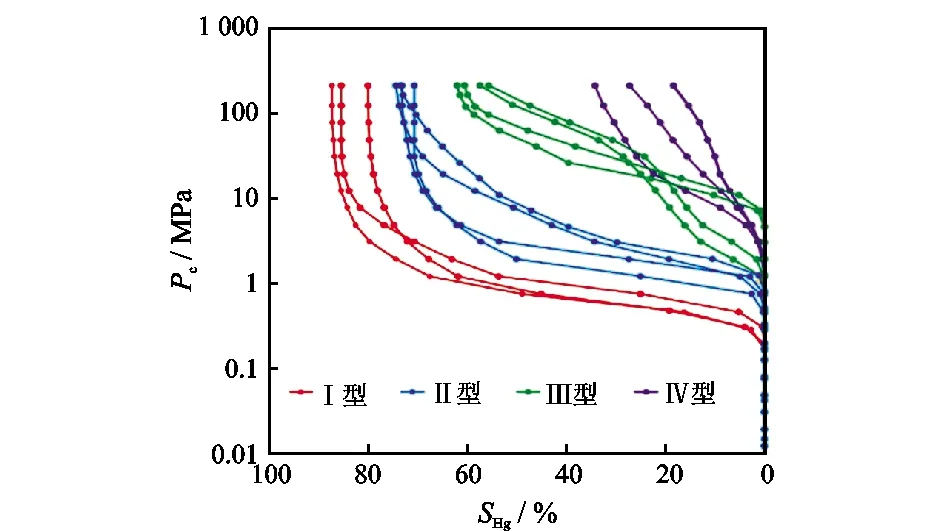
图5 延安气田东部盒8储层典型毛管压力曲线

2.2 实验设计

数据集由延安气田东部盒8段的岩心实验数据构成，采样位置见图3。其中训练集样本100个，测试集样本100个，训练集与测试集样本的构成要素一致。选取的特征参数由表征储层样品物性(孔隙度、渗透率)、孔喉大小(排驱压力、中值压力、中值半径)、孔喉分选性(喉道分选系数、歪度系数)以及孔喉连通性(最大进汞饱和度)组成。

样本特性如表1所示。使用主成分分析法，得到孔隙度、排驱压力、中值压力、最大进汞饱和度为权重最高的4个指标。因此，本次实验选择这4个特征参数，训练集所有样本进行归一化处理。在进行随机森林分类器训练前，需要配置分类器的参数。通常情况下，森林中决策树的数量和决策树的叶子数量对算法效率和分类精度影响较大。利用随机森林袋外误差评估分类器的性能，分析参数对结果的影响，从而选择合适的参数进行配置。参数配置完成后，使用训练集样本训练随机森林分类器。最后，在测试集上应用随机森林分类器，计算分类的进度和混淆矩阵，分析所训练分类器的性能。

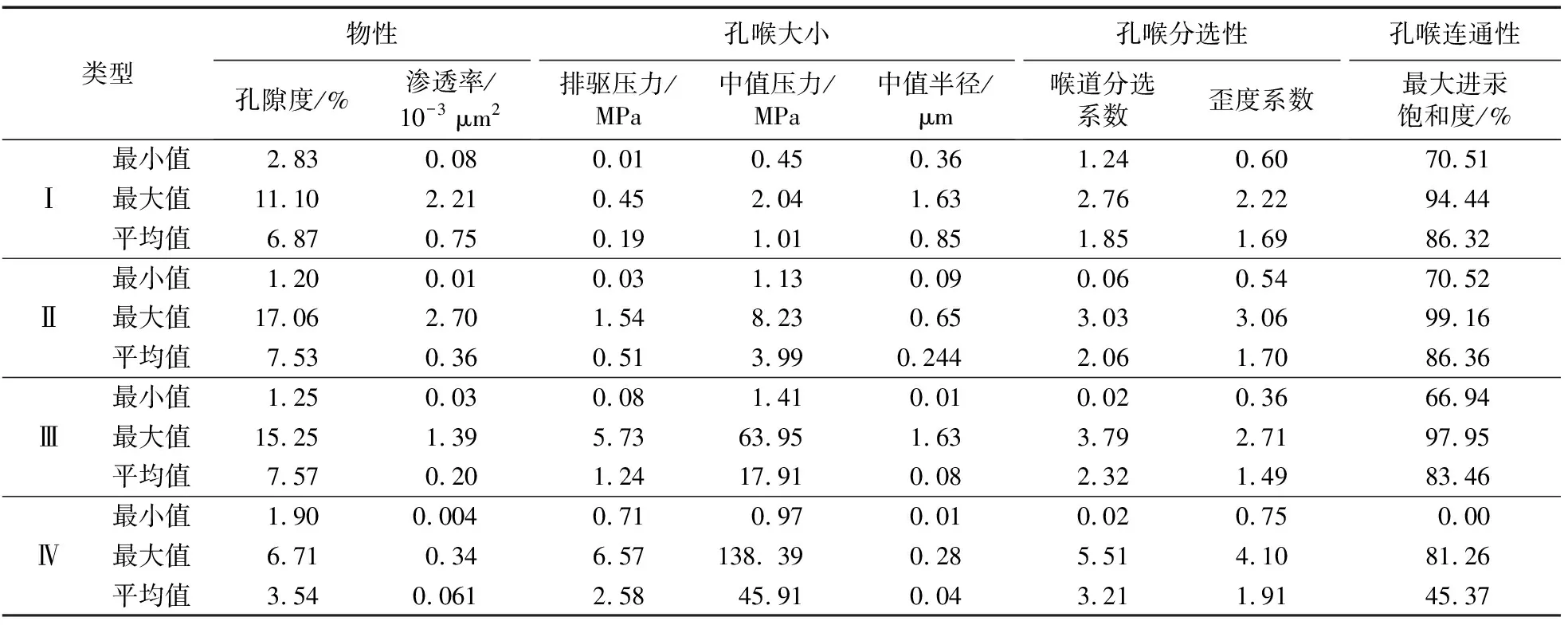
表1 样本特性

2.3 实验结果

随机森林中决策树叶子数量对袋外样本分类误差的影响曲线如图6所示。图中不同颜色的线条表示不同的决策树叶子数量。从图6可以看出，森林中决策树数量和决策树叶子数都直接影响袋外样本分类误差。决策树数量小于50棵，随着决策树叶子数量在0～20的区间内增加，分类误差逐渐降低。但是叶子数量进一步增大时，分类误差反而随之增大。这说明叶子数量不是越大越好，需要根据实际情况进行选择。

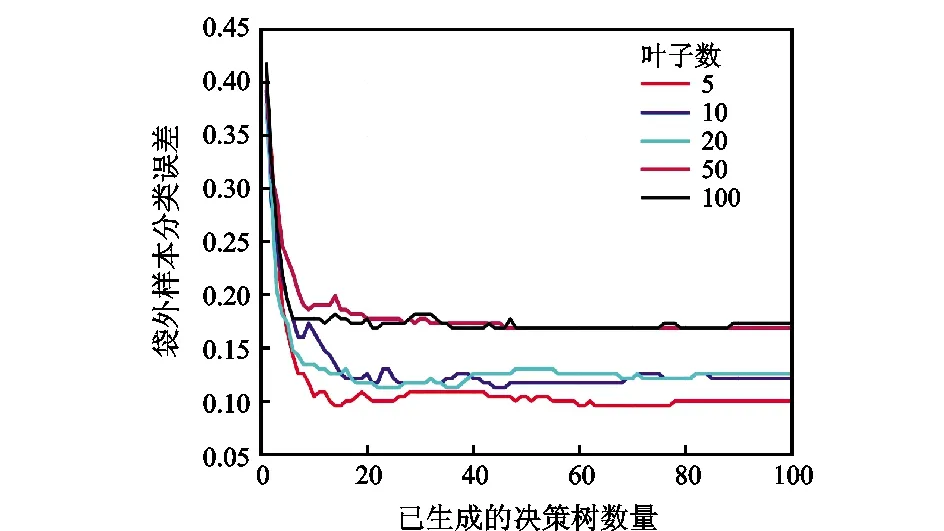
图6 叶子数量对袋外样本分类误差的影响曲线

随机森林中决策树数量分别为100和500棵时，袋外样本分类误差曲线和不含袋内样本的袋外样本分类误差曲线如图7—图10所示。由图可以得出，随机森林中决策树数量的增加，并不会出现过拟合现象。随机森林规模达到50棵以上时，分类器性能不会发生明显变化。从不含袋内样本的袋外样本分类误差来看，其数值与袋外样本分类误差相当。这说明分类器对样本的适应性较好。因此，综合考虑计算精度和计算效率，选择森林中决策树的数量为100和决策树的叶子数量为5进行随机森林分类器训练。随机森林训练完成的决策树如图11所示。

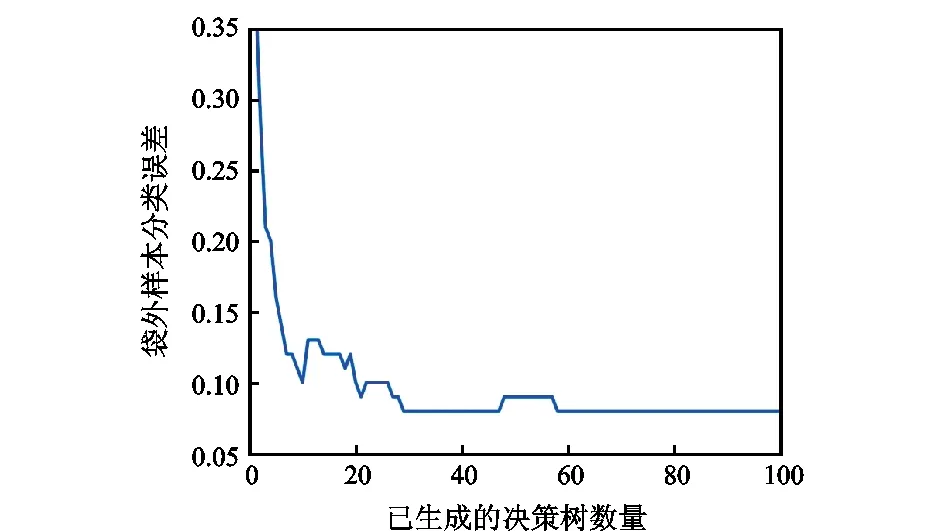
图7 袋外样本分类误差曲线(Trees=100)

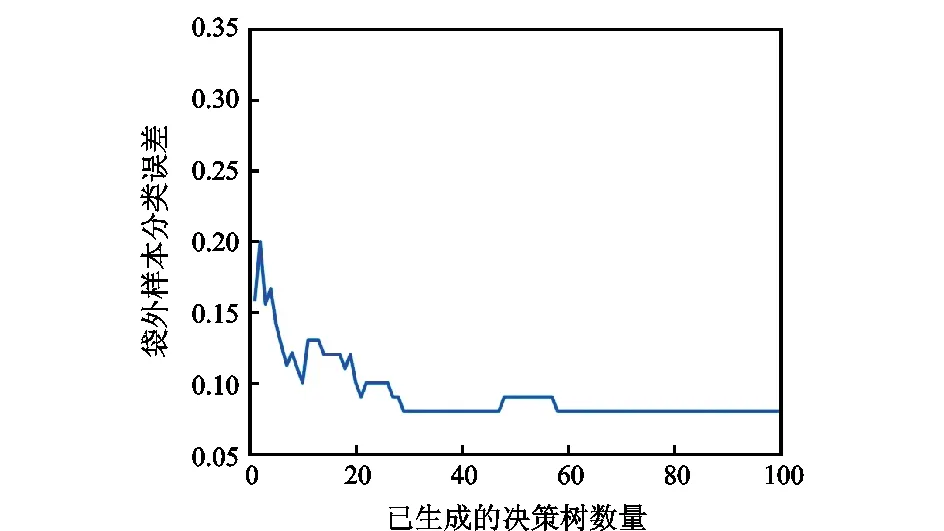
图8 不含袋内样本的袋外样本分类误差曲线(Trees=100)

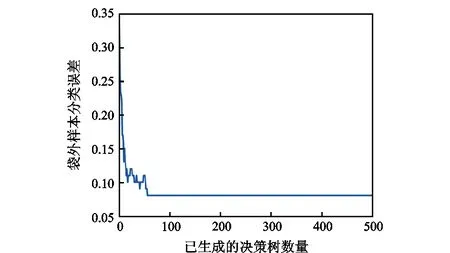
图9 袋外样本分类误差曲线(Trees=500)

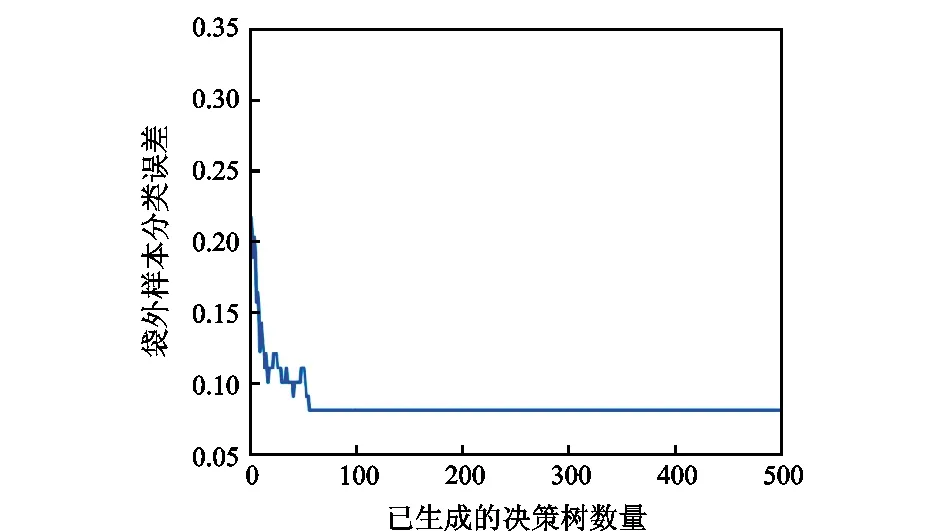
图10 不含袋内样本的袋外样本分类误差曲线(Trees=500)

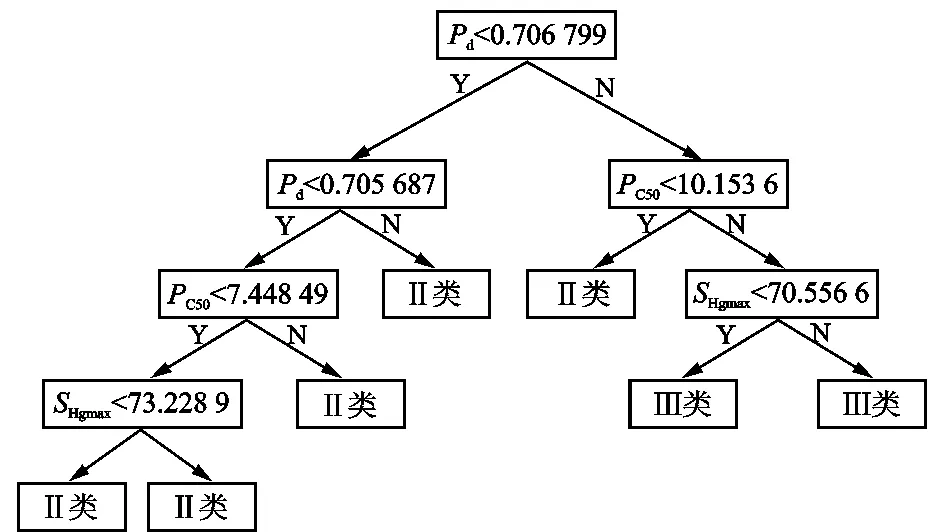
图11 随机森林中训练完成的某一棵决策树

利用训练完成的随机森林分类器，在测试集上进行测试，测试结果如表2所示。分类器的混淆矩阵如图12所示。训练集和测试集的模型精度分别为93.00%和89.10%，袋外样本分类误差和不含袋内样本的袋外样本分类误差均为8.00%。从随机森林分类器测试集的混淆矩阵可以看出，对Ⅰ类、Ⅱ类和Ⅲ类的分类准确率分别达到了100.00%、93.00%和98.00%，Ⅳ类的分类准确率相对较低，为67.00%。因此，可以得出所提出的随机森林算法非常适合于致密砂岩储层分类评价。该模型的精度足以提供可靠的预测结果。

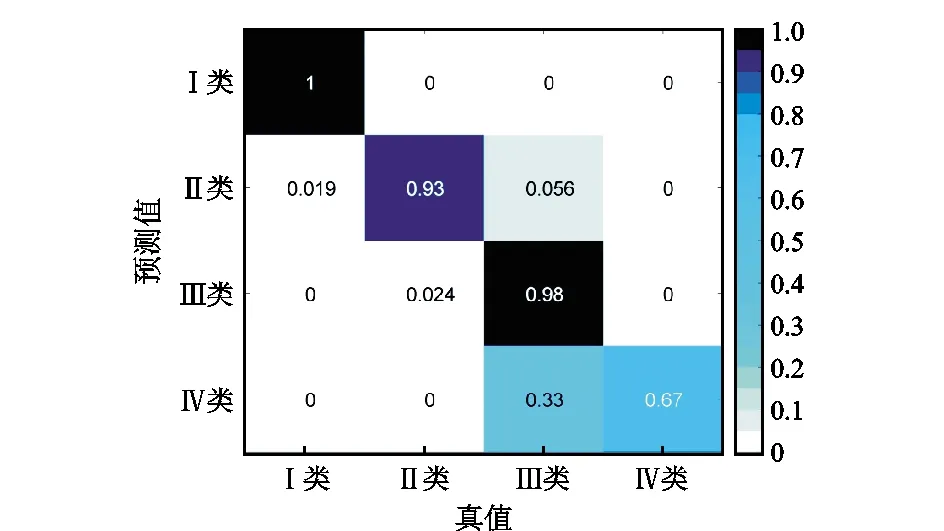
图12 测试集分类结果混淆矩阵

表2 算法训练结果

3 结 论

(1)随机森林算法可降低人为主观性的影响，提升储层分类效率。其分类结果更加准确客观，可以实际应用于致密储层的分类评价中。

(2)随机森林算法应用于储层分类评价时，参与分类的特征种类越多，其分类的精度和准度越高，但特征种类达到一定数量后，性能提升较缓慢。因此，需要选择合适的特征数量。基于主成分分析法计算得到的4个主要特征，用于随机森林的储层分类，取得了较高的分类精度。从延安气田东部盒8段的分类结果可以看出，随机森林分类器的精度高于89.10%，说明该算法在储层分类评价中有一定的应用潜力。